1 м3 1 м: Калькулятор пог. м. в м3 и м3 в пог. м онлайн
|
Величина
|
Единица
| |||||||
|
Наименование
|
Размерность
|
Наименование
|
Обозначение
| |||||
|
международное
|
русское
| |||||||
|
Пространство и время
| ||||||||
|
Площадь
|
L2
|
квадратный метр
|
m2
|
м2
| ||||
|
Объем, вместимость
|
L3
|
кубический метр
|
m3
|
м3
| ||||
|
Скорость
|
LT-1
|
метр в секунду
|
m/s
|
м/с
| ||||
|
Ускорение
|
LT—2
|
метр на секунду в квадрате
|
m/s2
|
м/с2
| ||||
|
Угловая скорость
|
Т+1
|
радиан в секунду
|
rad/s
|
рад/с
| ||||
|
Угловое ускорение
|
Т-2
|
радиан на секунду в квадрате
|
rad/s2
|
рад/с2
| ||||
|
Периодические явления, колебания и волны
| ||||||||
|
Период
|
Т
|
секунда
|
s
|
с
| ||||
|
Частота периодического процесса, частота колебаний
|
Т-1
|
герц
|
Hz
|
Гц
| ||||
|
Частота вращения
|
Т-1
|
секунда в минус первой степени
|
s—1
|
с-1
| ||||
|
Длина волны
|
L
|
метр
|
m
|
м
| ||||
|
Волновое число
|
L—1
|
метр в минус первой степени
|
m—1
|
м-1
| ||||
|
Коэффициент затухания
|
Т-1
|
секунда в минус первой степени
|
s—1
|
с-1
| ||||
|
Коэффициент ослабления, коэффициент фазы, коэффициент распространения
|
L—1
|
метр в минус первой степени
|
m—1
|
м-1
| ||||
|
Механика
| ||||||||
|
Плотность
|
L—3M
|
килограмм на кубический метр
|
kg/m3
|
кг/м
| ||||
|
Удельный объем
|
L3M-1
|
кубический метр на килограмм
|
m3×kg×
|
м3×кг
| ||||
|
Количество движения
|
LMT-1
|
килограмм-метр в секунду
|
kg×m/s
|
кг×м/с
| ||||
|
Момент количества движения
|
L2MT-1
|
килограмм-метр в квадрате на секунду
|
kg×m2/s
|
кг×м2/с
| ||||
|
Момент инерции (динамический момент инерции)
|
L2M
|
килограмм-метр в квадрате
|
kg×m2
|
кг×м2
| ||||
|
Сила, сила тяжести (вес)
|
LMT-1
|
ньютон
|
N
|
Н
| ||||
|
Момент силы, момент пары сил
|
L2MT—2
|
ньютон-метр
|
N×m
|
Н×м
| ||||
|
Импульс силы
|
LMT-1
|
ньютон-секунда
|
N×s
|
Н×с
| ||||
|
Давление, нормальное напряжение, касательное напряжение, модуль
продольной упругости, модуль сдвига, модуль объемного сжатия
|
L—1MT—2
|
паскаль
|
Pa
|
Па
| ||||
|
Момент инерции (второй момент) площади плоской фигуры- (осевой, полярный, центробежный)
|
L4
|
метр в четвертой степени
|
m4
|
м4
| ||||
|
Момент сопротивления плоской фигуры
|
L3
|
метр в третьей степени
|
m3
|
м3
| ||||
|
Динамическая вязкость
|
L—1MT—1
|
паскаль-секунда
|
Pa×s
|
Па×с
| ||||
|
Кинематическая вязкость
|
L2T—1
|
квадратный метр на секунду
|
nr/s
|
м2/с
| ||||
|
Поверхностное натяжение
|
MT | |||||||
Объемная масса инертных материалов | Песок и щебень в МО
Объемная масса пгс, песка, щебня
Дорогие строители и посетители сайта, мы собрали различные ГОСТ характеристики по щебню:
Как можно определить насыпную плотность?
Существует два способа!!!
Первый способ предлагает воспользоваться условными коэффициентами перевода, которые указаны ниже. Но в этом случае вы должны понимать, что таким образом результат будет примерным (погрешность 0.1-5%).
Второй способ — это провести замеры с помощью какого-нибудь сосуда, например ведра! Именно такой результат принесёт вам более истинный результат.
Насыпать сыпучий материал совком в мерный цилиндр, например ведро вместимостью 10 литров, с высоты 10 см, до того момента пока сосуд не заполнится «с горочкой». Эту «горочку» срезают вровень с краем мерного сосуда, опять же стараясь не уплотнять песок. После этого взвешиваем сосуд вместе с сыпучим материалом. Насыпная плотность пгс, песка, щебня — это отношение массы сыпучего материала (с вычетом массы сосуда) к занимаемому объему.
V нас.пл. = Масса сып.мат. / V сосуда
Перевод из 1 куб. м ПГС в 1 тонну.
Перевод из 1 куб. м песка в 1 тонну.
Перевод из 1 куб. м щебня в 1 тонну.
Очень часто наших клиентов мучает вопрос, как перевести кубические метры в тонны и наоборот. На данной странице мы попытались рассмотреть способ с помощью коэффициента перевода.
Таблица коэффициентов перевода м3 в тонны для сыпучих материалов:
Наименование материала | Объём | Коэффициент | Вес |
ПГС | 1 м3 | 1,65 | 1,65 тн |
Песок природный | 1 м3 | 1,4 | 1,4 тн |
Песок речной | 1 м3 | 1,5 | 1,5 тн |
Щебень фр.5-10, М-1200 | 1 м3 | 1,43 | 1,43 тн |
Щебень фр.5-20, М-1200 | 1 м3 | 1,40 | 1,40 тн |
Щебень фр.20-40, М-1200 | 1 м3 | 1,38 | 1,38 тн |
Перевести тонны в кубометры. Калькулятор
Перевод тонн в кубометры и обратно осуществляется для определения объёма материала (вещества), имеющего определенную массу, или же для расчёта
веса материала, который содержится в заданном объёме. Например, нужно определить вес трёх кубометров песка, или высчитать объём,
который займут пять тонн щебенки. Чтобы быстро перевести кубические метры в тонны или обратно, используйте калькулятор.
Для решения этих задач необходимо знать плотность вещества. Но следует учитывать, что плотность многих веществ неоднозначна
(например, разные марки цемента имеют разную плотность), поэтому, чем точнее Вы определите плотность (из справочника или из документации),
тем точнее будут Ваши расчёты.
Применяемая формула
M = p * V
где
M — масса
p — плотность материала
V — объём
Примеры решения
Задача 1
Какую массу будут иметь 3 кубических метра бетонного раствора плотностью 2250 кг/м3?
Решение
M = 3 м3 * 2250 кг/м3 = 3 м3 * 2,25 т/м3 = 6,75 т
Задача 2
Какой объем будут занимать 5 тонн мелкозернистого асфальта?
Решение
Плотность мелкозернистого асфальта составляет 2330 кг/м3. Вычисляем объём по формуле
V = 5 т : 2330 кг/м3 = 5 т : 2,33 т/м3 = 2,146 м3
Калькулятор тонн и кубометров
Перевести
Поделитесь этой страницей с друзьями
Другие конвертеры
Перевести квадратные метры в кубические
Перевести литры в килограммы
Разбираемся, что такое и сколько Гкал в 1 м3 горячей воды, как правильно сделать расчет?
Что это такое и сколько в 1 кубическом метре?
Количество энергии, расходуемой на подогрев воды, измеряется в калориях. Затраченное для нагрева одного грамма воды на один градус количество энергии — это одна калория.
1 м — 1000 Кг или 1000 000 г.
Составляем пропорцию:
- 1 кал 1 г;
- Х кал 1000 000 г, отсюда х=1000 000 кал.
Следовательно, на нагрев расходуется 1000 000 калорий или в общепринятых единицах 0,001 Гкал.
Когда необходим перевод из гигкалорий в кубометры?
Ресурсоснабжающие организации в счетах на отопление указывают затраченные гигакалории.
В новостройках внедрен общедомовой и поквартирный учет расхода теплоэнергии.
В старом жилом фонде комплектация приборами учета тепловодоснабжения технически сложна, в этом случае пригодится умение преобразовывать Гкал в 1 м3 горячей воды.
Как рассчитать сколько гигкалорий в куб. метре на примере
Меры энергии и объема — различные величины. Несложные вычисления помогут их сопоставить.
Пример: Температура теплоносителя в многоквартирном доме должна быть не менее 55 ⁰С, температура холодной воды примерно 5 ⁰С.
Для нагрева кубометра понадобится:
(55-5)×0,001=0,05 Гкал.
Потери тепла из-за несовершенства теплоизоляции неизбежны, в расчеты закладываются потери на уровне 20%. Значит, фактически для нагрева потребуется 0,06 Гкал.
Это соотношение позволяет по теплосчетчику определять расход нагретой воды.
Пример: в стоквартирном жилом доме прибор учета тепловой энергии показал в летний период, когда расходуется только теплоноситель для бытовых нужд, 150 Гкал. В 20 квартирах расход горячей воды определяется индивидуальными счетчиками, общий расход по этим квартирам составил 400 м³.
Весь дом потребляет: 150÷0,06=2500 м³. Значит, на остальные квартиры приходится: 2500-400=2100 м³. Далее 2100м³ делится на фактическое число жильцов.
Такая методика позволяет переводить значения тепловой энергии в объемные показатели расхода теплоносителя и наоборот.
В домах с открытой системой отопления разница показаний водомеров на подающей и обратной трубах покажет количество теплоносителя, расходуемого на отопление, и после пересчета расход теплоэнергии.
Расчеты носят справочный характер и служат для контроля расхода тепловодоснабжения.
Как считается плата за теплоснабжение?
Если водоснабжение для бытовых нужд оценивается внутриквартирными приборами учета или утвержденными нормативами, то плата за теплоснабжение рассчитывается на основе утвержденных методик.
По срокам начислений применяются два варианта:
- За отопительный сезон.
- За календарный год.
Методика расчета затрат на теплоснабжение зависит от нескольких факторов:
- от вида смонтированной системы горячего водоснабжения: открытой или закрытой;
- от наличия общедомовых и внутриквартирных приборов учета тепловодоснабжения.
Логика расчетов едина: распределение всей потребляемой домом тепловой энергии по площади жилых и нежилых отапливаемых помещений, т.е. жильцы оплачивают часть затрат пропорционально занимаемой отапливаемой площади.
Плата за отопление равна: P = Q×S×T, где:
- Q — количество потребляемой тепловой энергии на 1 м3 занимаемой площади, включая общедомовые расходы;
- S — занимаемая площадь;
- T — установленный органами местной власти тариф за тепловую энергию.
Тарифы ежегодно пересматриваются и утверждаются для каждой системы теплоснабжения индивидуально.
Заключение
Плата за коммунальные услуги регулярно растет. Для сохранения семейного бюджета нужно уметь оценивать качество оказываемых услуг и их стоимость. Квалифицированный анализ нередко приводит к перерасчету коммунальных платежей в сторону их уменьшения.
2
.
Три груза массами m1 = 1, m2 = 2, m3 = 3 кг соединены легкими нитями, проходящими кг
Условие задачи:
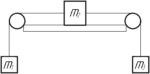Три груза массами \ (m_1 = 1 \), \ (m_2 = 2 \) кг, \ (m_3 = 3 \) кг соединены легкими нитями, проходящими через неподвижные блоки, установленные на краях стола. Коэффициент трения второго тела о стол 0,5. Определите ускорение.
Задача №2.2.2 из «Сборника задач подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\ (m_1 = 1 \) кг, \ (m_2 = 2 \) кг, \ (m_3 = 3 \) кг, \ (\ mu = 0,5 \), \ (a -? \)
Решение задачи:
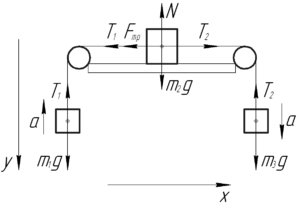Изобразим на схеме все тела и покажем силы, действующие на них.Сначала разберемся со вторым телом. Оно не двигается вдоль оси \ (y \), значит по первому закону Ньютона в проекции на эту ось верно записать следующее:
\ [N = {m_2} g \; \; \; \; (1) \]
На второе тело действует сила трения скольжения , которая определяется по формуле:
\ [{F_ {тр}} = \ mu N \]
Учитывая (1), получим:
\ [{F_ {тржения }} = \ mu {m_2} g \]
Далее силу трения будем подставлять таким полученным выражением.
Так как все грузы двигаются с некоторым одинаковым ускорением, запишем второй Ньютона для каждого груза в проекции на ось, вдоль которой движется каждое тело:
\ [\ left \ {\ begin {gather}
{m_3} g — {T_2} = {m_3} a \ hfill \\
{T_2} — \ mu {m_2} g — {T_1} = \ hfill \\
{m_1} g — {T_1} = — {m_1} a \ hfill \\
\ end {gather} \ right. {m_2} a \]
Прибавим к первому выражению системы второе и отнимем третье, после получим:
\ [{m_3} g — \ mu {m_2} g — { m_1} g = {m_3} a + {m_2} a + {m_1} a \]
\ [g \ left ({{m_3} — \ mu {m_2} — {m_1}} \ right) = a \ left ({{m_1} + {m_2} + {m_3}} \ right) \]
Отсюда искомое ускорение \ (a \) равно:
\ [a = \ frac {{g \ left ({{m_3} — \ mu {m_2} — {m_1}} \ right)}} {{{m_1} + {m_2} + {m_3}}} \]
Посчитаем ответ:
\ [a = \ frac {{10 \ cdot] \ left ({3 — 0,5 \ cdot 2 — 1} \ right)}} {{1 + 2 + 3}} = 1,67 \; м / с ^ 2 \]
Ответ: 1,67 м / с 2 .
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставьте ниже комментарий.
.