3 к 1 пропорция: Пропорция 1 к 3 – это сколько?

Содержание

Как составить и рассчитать пропорцию: онлайн калькулятор

Онлайн калькулятор пропорций

Формула пропорций

Пропо́рция — это равенство двух отношений, когда a:b=c:d

средние
		╭	члены	╮
1	:	10	=	7	:	70
╰	крайние члены					╯

0,1			=	0,1

1 10 = 7 70

Основные свойства пропорции

Произведение крайних членов равно произведению средних членов (крест-накрест): если a:b=c:d, то a⋅d=b⋅c

1
10 ✕ 7
70

1 ⋅ 70 = 10 ⋅ 7

Обращение пропорции: если a:b=c:d, то b:a=d:c

Перестановка средних членов: если a:b=c:d, то a:c=b:d

Перестановка крайних членов: если a:b=c:d, то d:b=c:a

Решение пропорции с одним неизвестным | Уравнение

1 : 10 = x : 70



1
10 = x
70

Чтобы найти икс, нужно перемножить два известных числа крест-накрест и поделить на противоположное значение

x = 1 ⋅ 70
10 = 7

Как посчитать пропорцию

Задача: нужно пить 1 таблетку активированного угля на 10 килограмм веса. Сколько таблеток нужно выпить, если человек весит 70 кг?

Составим пропорцию:
1 таблетка — 10 кг
x таблеток — 70 кг

Чтобы найти икс, нужно перемножить два известных числа крест-накрест и поделить на противоположное значение:
1 таблетка
x таблеток ✕ 10 кг
70 кг

x = 1 ⋅ 70 : 10 = 7

Ответ: 7 таблеток

Задача: за пять часов Вася пишет две статьи. Сколько статей он напишет за 20 часов?

Составим пропорцию:
2 статьи — 5 часов 
x статей — 20 часов

x = 2 ⋅ 20 : 5 = 8

Ответ: 8 статей

Будущим выпускникам школ могу сказать, что умение составлять пропорции мне пригодилось и при расчёте процентов, и для того, чтобы пропорционально уменьшать картинки, и в HTML-вёрстке интернет-страницы, и в бытовых ситуациях.

Пропорциональное деление. Деление на пропорциональные части

Пропорциональное деление — деление какой-нибудь величины на части, прямо или обратно пропорциональные данным числам.

Чтобы разделить число на части пропорционально нескольким данным числам, надо разделить его на сумму этих чисел и частное умножить на каждое из них.

Деление числа на пропорциональные части

Пример 1. Разделить число 50 на части пропорционально числам 2 и 3.

Решение: Надо найти такие два слагаемых числа 50, которые будут относиться друг к другу так, как 2:3. Первое слагаемое должно содержать 2 части числа, а второе 3, значит, число 50 содержит 5 таких частей (2 + 3 = 5), следовательно, каждая такая часть будет равна:

50 : 5 = 10.

Число 10 — одна часть. Теперь надо умножить эту часть на числа, пропорционально которым требовалось разделить число 50:

10 · 2 = 20;

10 · 3 = 30.

Ответ: 2:3 = 20:30.

Пример 2. Разделить число 90 на три слагаемых пропорционально числам 1, 2 и 3.

Решение:

90 : (1 + 2 + 3) = 90 : 6 = 15;

1 · 15 = 15;

2 · 15 = 30;

3 · 15 = 45.

Ответ: 1:2:3 = 15:30:45.

Длинные отношения вида 1:2:3 называются сложными. Сложные отношения — это условные записи, показывающие, сколько долей содержит каждая часть. Если члены сложного отношения дробные, то, приведя их к общему знаменателю и умножив на него, можно заменить отношение дробных чисел отношением целых.

Пример. Разделить число 66 на такие три части, чтобы первая относилась ко второй, как 3:2, а вторая к третьей, как 5:4.

Решение:

Первый способ: обозначим искомые части буквами a, b и c. Так как отношение не изменится, если оба члена умножить на одно и то же число, то умножим члены первого отношения на 5, а второго на 2:

a:b = 3:2 = 15:10;

b:c = 5:4 = 10:8;

значит a:b:c = 15:10:8. Так как 15 + 10 + 8 = 33, то

a = (66 : 33) · 15 = 30;

b = (66 : 33) · 10 = 20;

c = (66 : 33) · 8 = 16.

Второй способ: обозначим искомые части буквами a, b и c:

a:b = 3:2;

b:c = 5:4.

Если первая часть a равна 3, вторая b равна 2, то третью часть c можно определить из пропорции:

2:c = 5:4.

Следовательно, c равно:

c =	2 · 4	=	8	,
	5		5

поэтому

Умножив все члены полученного сложного отношения на 5, чтобы избавиться от дробного члена, получим:

a:b:c = 15:10:8,

так как 15 + 10 + 8 = 33, то

a = (66 : 33) · 15 = 30;

b = (66 : 33) · 10 = 20;

c = (66 : 33) · 8 = 16.

Деление на части, обратно пропорциональные числам

Пример. Разделить число 62 на три части обратно пропорционально числам 2, 3 и 5, то есть разложить на три части, которые относились бы между собой, как

Решение: Обозначим искомые части буквами a, b и c. Приведём члены отношения к общему знаменателю и заменим дробные члены на целые числа:

a:b:c =	1	:	1	:	1	=	15	:	10	:	6	= 15:10:6,
	2		3		5		30		30		30

так как 15 + 10 + 6 = 31, то

a = (62 : 31) · 15 = 30;

b = (62 : 31) · 10 = 20;

c = (62 : 31) · 6 = 12.

Соотношение сторон видео | Пропорции видео

Если вы часто скачиваете кино из Интернета или загружаете собственные клипы на YouTube и другие сайты, вы наверняка сталкивались с искажением картинки в видеофайлах.

Возможно, вы были разочарованы сплющенным и растянутым изображением в фильме, который долго искали. Или были неприятно удивлены черной рамкой, которая появляется вокруг изображения после загрузки клипа на сайт. Причина таких проблем кроется в неправильном соотношении сторон кадра, установленном при сохранении видеофайла. Стоит исправить эту ошибку – и видео будет радовать глаз правильными пропорциями и отсутствием ненужных элементов вроде черного обрамления картинки.

Яснее не стало? Прочтите нашу статью, и вы не только узнаете, что такое соотношение сторон видео, но и научитесь выявлять и исправлять проблемы, связанные с неправильным значением этого параметра.

Что такое пропорции видео?

Видеоряд любого фильма или клипа состоит из большого числа одинаковых по размеру кадров, размер каждого из которых характеризуется двумя величинами: шириной (длиной кадра по горизонтали) и высотой (длиной кадра по вертикали). Так вот, пропорция ширины и высоты кадра – и есть соотношение сторон видео. Эта величина обозначается двумя цифрами, разделенными двоеточием (2:1, 4:3 и т. д.).

Вариантов соотношения сторон существует немало, однако на сегодня наиболее распространены два: 4:3 и 16:9 (см. рисунок). Поскольку соотношение сторон 16:9 наиболее близко к тому, как человек видит окружающее пространство, именно этот формат сегодня наиболее популярен. Определенную популярность также набирает соотношение сторон 21:9 – для мониторов с ультрашироким экраном.

Как узнать соотношение сторон видеоклипа?

Когда мы говорим о соотношении сторон видеоклипа, обычно мы имеем в виду характеристику DAR (Display Aspect Ratio) – соотношение сторон, с которым запись отображается на экране. DAR зависит от двух величин:

Pixel Aspect Ratio (PAR) – соотношение сторон пикселя. Поскольку в современном цифровом видео, как правило, используются только квадратные пиксели, для большинства «компьютерных» видеофайлов эта величина всегда будет равна 1:1.

Storage Aspect Ratio (SAR) – отношение количества пикселей по горизонтали к количеству пикселей по вертикали (эти цифры указаны в разрешении видеофайла).

Умножив PAR на SAR, мы получаем DAR – фактическое соотношение сторон видеоклипа.

Разберем на примере. Допустим, нам нужно узнать соотношение сторон видеоклипа в формате AVI с разрешением 640 × 480. Чтобы вычислить SAR, нам нужно разделить ширину видеофайла (640) на высоту (480) до простой дроби. Получаем 4/3. Поскольку, как мы уже выяснили, PAR нашего видео равно единице, соотношение 4:3 и будет являться соотношением сторон видеоклипа.

К слову, значения DAR и SAR совпадают не всегда. Например, в стандартах VCD и DVD видеозаписи кодируются с использованием неквадратных пикселей, соотношение сторон которых не равно 1:1. Чтобы разобраться, давайте посчитаем DAR для DVD-видео с распространенным разрешением 720 × 576. В этом случае SAR будет равно 5:4, а PAR, согласно стандарту, – 16:15. Перемножив эти значения, получим все то же соотношение сторон 4:3.

Нет времени считать вручную? Если у вас установлен Movavi Конвертер Видео, вам повезло – эта умная программа сделает все за вас! Просто загрузите свое видео в конвертер, кликните по нему правой кнопкой мыши, выберите пункт Свойства файла, и вы увидите нужные цифры.

Какие бывают стандартные разрешения и какие соотношения сторон для них используются?

Наиболее часто используемые разрешения и соотношения сторон для них приведены в следующей таблице.

Какое соотношение сторон рекомендуется для YouTube?

Тут все просто: на сайте популярного видеохостинга соотношение сторон составляет 16:9, в противном случае к видео добавляются черные полосы.

Как выявить проблемы неправильного соотношения сторон?

При проигрывании видео, сохраненного с неверным соотношением сторон, вы увидите в кадре один из следующих дефектов:

Искажение пропорций. Изображение выглядит вытянутым или, напротив, сплющенным.

Нежелательные черные полосы по вертикали или горизонтали либо черную рамку вокруг изображения на видео.

Иногда такие проблемы возникают из-за неправильных настроек дисплея проигрывающего устройства. Однако если все настройки верны, а изображение на экране вас по-прежнему не радует, нужно поменять соотношение сторон самого видеофайла – в Movavi Конвертере Видео это можно сделать легко и быстро. Достаточно поставить программу на компьютер и выполнить несколько простых шагов.

Как исправить пропорции видео при помощи Movavi Конвертера Видео?

Запустите Movavi Конвертер Видео.
Нажмите Добавить файлы, а затем Добавить видео. Загрузите «проблемное» видео в программу.
Раскройте вкладку Видео в нижней части интерфейса и выберите любой профиль нужного формата. После этого нажмите на кнопку со значком шестеренки.
В диалоговом окне выберите в списке Размер кадра пункт Пользовательский. Перейдите к полям Ширина и Высота в правой части, нажмите на значке с изображением скрепки, чтобы разблокировать поля, и введите подходящие значения.
В списке Изменение размера выберите опцию Кадрировать, чтобы убрать черную рамку вокруг изображения. В списке Качество вы можете выбрать нужный вам вариант.
Нажмите Старт – и через несколько минут сможете наслаждаться видео с нужными пропорциями.

Онлайн урок: Прямая и обратная пропорциональные зависимости по предмету Математика 6 класс

Давайте сначала разберемся, что такое пропорциональность.

Пропорциональность — это зависимость двух величин друг от друга таким образом, что значение отношения этих величин остается постоянным.

Зависимость величин друг от друга может быть прямой и обратной.

Отношение между величинами описываются прямой или обратной пропорциональностью.

Прямая пропорциональность выражается так: \(\mathbf{y = kx}\)

Обратная пропорциональность выражается так: \(\mathbf{y = \frac{k}{x}}\)

где k — это число, которое называют коэффициентом пропорциональности.

x и y величины, зависящие друг от друга.

Пример

Площадь прямоугольника равна \(\mathbf{S = a \cdot b}\), где S— это площадь прямоугольника, а — длина прямоугольника, b — ширина прямоугольника.

Если один из множителей произведения — постоянная величина, то произведение прямо пропорционально второму множителю.

Если постоянно значение произведения, то множители зависят друг от друга обратно пропорционально.

По формуле видно, что площадь квадрата зависит от длины (ширины) его стороны, а длина стороны (ширина) зависит от его площади.

Какова эта зависимость, сейчас и рассмотрим.

\(\mathbf{S = a \cdot b}\)

Зависимость площади прямоугольника от длины при постоянном значении ширины является прямо пропорциональной зависимостью этих величин.

Зависимость площади прямоугольника от ширины при постоянном значении длины является прямо пропорциональной зависимостью этих величин.

\(\mathbf{a = \frac {S}{b}}\) или \(\mathbf{b = \frac {S}{a}}\)

Пусть одна клетка равна 1 см. Рассмотрим рисунок:

Ширина прямоугольника b постоянная величина

b = 4 см

a₁ = 6 см

Увеличим ширину прямоугольника — сторону a₁ на 1 см,получим

a₂ = 7 см

Найдем площади прямоугольников S₁ и S₂

\(\mathbf{S_{1} = a_{1} \cdot b = 6 \cdot 4 = 24}\) см²

\(\mathbf{S_{2} = a_{2} \cdot b = 7 \cdot 4 = 28}\) см²

Вывод: при увеличении стороны прямоугольника увеличилась площадь прямоугольника.

Рассмотрим другой вариант зависимости

Зависимость одной из сторон прямоугольника от второй стороны при постоянном значении площади прямоугольника является обратно пропорциональной зависимостью. Пусть одна клетка равна 1 см

Площадь прямоугольника S постоянная величина

S = 24 см²

b₁ = 4 см

\(\mathbf{a_{1} = \frac{S}{b_{1}} = 6}\) (см)

Увеличим высоту прямоугольника- сторону прямоугольника b₁ на 2 см_,получим

b₂ = 6 см

Найдем ширину прямоугольника- сторону a₂

\(\mathbf{a_{2} = \frac{S}{b_{2}} = 4}\) (см)

Вывод: при увеличении одной стороны прямоугольника и постоянном значении площади, вторая сторона уменьшается.

Таким образом, мы подошли к основным понятиям пропорциональной зависимости. Чтобы было легко разобраться в несложных схемах ниже, мы дадим пояснение символам:

Итак:

1) Две величины прямо пропорциональны друг другу, если при увеличении (уменьшении) одной величины в n количество раз, другая величина, зависящая от первой, так же увеличивается (уменьшается) в n количество раз.

2) Две величины обратно пропорциональны друг другу, если при увеличении (уменьшении) одной величины в n количество раз, другая величина, зависящая от первой, уменьшается (увеличивается) в n количество раз.

Примеров прямой и обратной пропорциональности множество.

Однако не все величины зависят друг от друга прямо пропорционально или обратно пропорционально, встречаются и более простые и более сложные зависимости величин.

Надо понимать, что даже если какие-нибудь две величины возрастают или убывают, то между ними не обязательно существует пропорциональная зависимость.

Например, с течением времени увеличивается возраст человека и его размер ноги, но эти величины не являются пропорциональными, так как при удвоении возраста размер ноги человека не удваивается

Как соотношение сторон фотографии влияет на композицию на примере пейзажной съемки

Выбор композиции часто является тем самым ключом понимания между хорошей пейзажной фотографией и отличной пейзажной фотографией.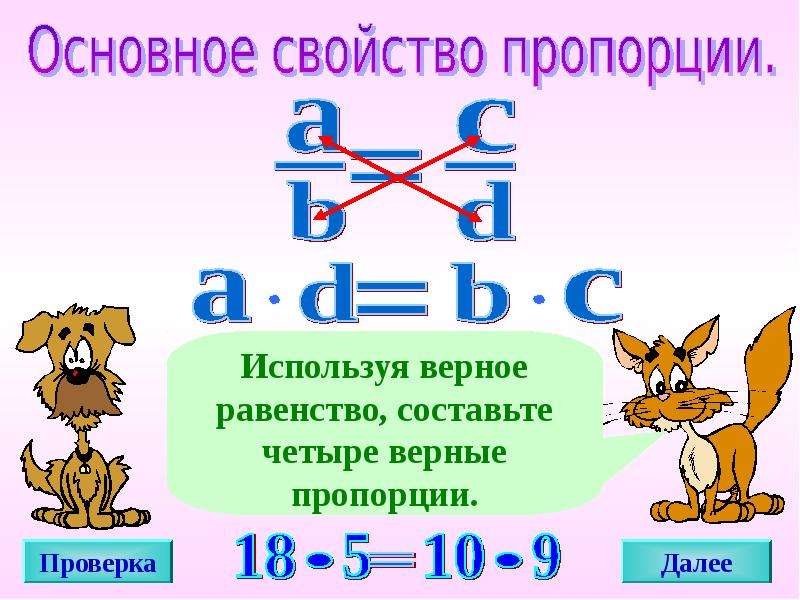 А вот соотношение сторон фотографии может создавать или разрушать композицию, подчеркнуть объект и устранить отвлекающие факторы, либо вывести из равновесия всю картину. Когда вы смотрите в видоискатель и собираетесь нажать кнопку спуска затвора полезно попытаться представить себе финальный снимок, включая и его соотношение сторон, чтобы оптимизировать композицию.

by Andrew S.Gibson

Но как соотношение сторон влияет на композицию?

Соотношение сторон — это термин, используемый для описания размеров изображения путем сравнения ширины с высотой и выражения в виде соотношения.

Соотношение сторон изображений в первую очередь определяется размерностью датчика камеры (или типом пленки плюс дизайном камеры, если фотоаппарат пленочный). Поскольку эти физические аспекты являются фиксированными, легко принять соотношение сторон изображений как должное и особо не задумываться над последствиями установленного их соотношения, которое и используется в композиции.

Производители камер осознали, что иногда фотографам нравится работать с широким диапазоном вариантов, а самые последние цифровые камеры позволяют изменять параметр соотношения сторон с помощью меню камеры. Вы также можете кадрировать изображение, чтобы затем изменить параметр при постобработке.

Почему соотношение сторон имеет значение

Значимость этого понятия связана с отношением основного объекта к сторонам кадра и количеством свободного пространства вокруг объекта.

Знание характеристик соотношения сторон вашей конкретной камеры может помочь создавать более качественные изображения. Это также поможет вам распознать, когда кадрирование до другого соотношения сторон может улучшить композицию полученной картинки.

Что же такое соотношение сторон?

Соотношение сторон описывает связь между шириной и высотой изображения. Записывается как фигура, в этой форме — ширина:высота (ширина всегда на первом месте).

Практически каждая цифровая камера оснащена датчиком одного из двух форматов изображения.

3:2

Это соотношение, используемое 35-миллиметровым камерами с кроп-фактором и полнокадровыми зеркальными фотоаппаратами, некоторыми среднеформатными камерами Leica, беззеркальными камерами, компактными фотоаппаратами высокого класса и большинством 35-мм пленочных камер.

Оно было у нас с тех пор, как в начале прошлого века Leica выпустила первые 35-мм пленочные камеры. 35-миллиметровый камеры с кроп-фактором и полнокадровые зеркалки имеют соотношение сторон 3:2. Ширина датчика в 1,5 раза больше его высоты.

35-миллиметровый сенсор для полнокадрового изображения имеет размеры 36×24 мм. Вы можете выразить это как соотношение 36:24. Математикам всегда нравится упрощать соотношения между двумя числами так, чтобы его было легко визуализировать. В этом случае можно разделить оба измерения на двенадцать. Это дает 3:2. Камеры с кроп-фактором имеют меньшие датчики размером примерно 22,5×15 мм (точные размеры варьируются в зависимости от марки и модели). Эти цифры соответствуют соотношению сторон 3:2 для полнокадрового датчика.

4:3

Это соотношение сторон используется микрокамерами, многими компактными камерами, некоторыми цифровыми камерами среднего формата и пленочными среднего формата, использующими формат 6×4,5 см.

Давайте сравним их. Вы можете увидеть, что формат 3:2, используемый большинством цифровых зеркальных фотокамер, немного длиннее, чем 4:3 для микрокамер.

Это может показаться не так значительно, однако важно для композиции. Посмотрите на следующие изображения, чтобы понять почему. Ниже фотография оригинальной 35-мм версии с соотношением сторон 3:2.

И вот то же изображение, обрезанное до соотношения сторон 4:3, как если бы оно было снято на микрокамеру 4:3.

Видите разницу? Она тонкая, однако, все же присутствует. 35 мм кадр длиннее. И задача может оказаться довольно сложной, когда дело доходит до композиции, потому что вы должны найти способ эффективного заполнения такой длины. Пейзажная фотография, в частности, часто выигрывает от более короткого кадра, и это одна из причин популярности среднего формата 6×7 см (соотношение сторон 7:6) среди пейзажных фотографов, которые используют пленочные камеры. Вот как будет выглядеть тот же пейзаж в следующих форматах.

Соотношение сторон 7:6 может показаться слишком коротким, а вот 5:4 — очень приятный формат для работы.

Вам может показаться, что разница между пропорциями не имеет какого-то особо большого значения. И часто, когда вы используете альбомный формат (т.е. камеру, расположенную так, чтобы кадр был горизонтальным), разница минимальна. Не так сложно работать в любом из вышеперечисленных форматов.

Но переключитесь на портретный формат (вертикальный кадр), и это будет уже совсем другая история. 35-миллиметровый кадр внезапно становится намного труднее эффективно заполнить, и композиция часто выигрывает от кадрирования до более короткого прямоугольника. Ниже вы видите несколько примеров для демонстрации этого эффекта.

Трудность, с которой фотограф столкнулся в съемке пейзажа заключается в том, что на исходном изображении было слишком много пустого неба. Проблема решилась путем кадрирования. Соотношение сторон 4:5, кажется, работает хорошо.

Конечно, не все изображения выиграют от обрезки до более короткого прямоугольника. Но если вам трудно заполнить кадр, особенно если у вас есть 35-мм камера с соотношением сторон 3:2, то вы вполне можете выиграть от использования другого формата кадра.

Настройка соотношения сторон в камере

Многие современные цифровые камеры дают вам возможность регулировать соотношение сторон с помощью меню камеры. Если в вашей камере есть электронный видоискатель, она может в нем отображать обрезанное изображение.

Если ваша камера не имеет электронного видоискателя, вам нужно будет использовать режим Live View, чтобы воспользоваться функцией соотношения сторон. Камера отобразит обрезанное изображение на ЖК-экране камеры.

Вы должны знать, что если вы используете формат JPEG, то камера обрезает изображение, и обрезанную часть изображения вы восстановить уже не сможете. Если вы используете RAW, камера сохранит изображение, захваченное всем датчиком, и вы сможете принять решение о кадрировании при последующей обработке. Проверьте подробности в руководстве к камере, если у вас есть какие-либо сомнения.

Кадрирование в постобработке

Зачастую при последующей обработке обрезать кадр проще. Если у вашей камеры нет функции соотношения сторон, это остается единственным вариантом. Еще одним преимуществом такого способа является то, что вы можете вернуться к старым изображениям, чтобы понять, как лучше.

Теперь рассмотрим каждый формат более подробно.

1:1 — квадрат

Квадратный формат часто может использоваться, чтобы упростить изображение и дать объекту поразительное присутствие в центре кадра. Если оставить ширину равной высоте, то способ считывания фотографии у зрителя изменится, так как надобность перемещаться по кадру слева направо бу

Пропорции человека. Для рисующих и прочих :))): 3d_tutorials — LiveJournal

LiveJournal

Main
Ratings
Interesting
iOS & Android
Disable ads

Login
CREATE BLOG
Join
English
(en)
- English (en)
- Русский (ru)
- Українська (uk)
- Français (fr)
- Português (pt)
- español (es)
- Deutsch (de)
- Italiano (it)
- Беларуская (be)

Соотношение и пропорции. Эволюция реальных чисел.

Этот урок продолжается с урока 2.

Теорема об альтернативной пропорции

Теорема об одном и том же кратном

Теорема об общем делителе

Самые низкие сроки

Теорема крайностей и средств

Язык соотношения

ПРОПОРЦИЯ ЯВЛЯЕТСЯ ЗАЯВЛЕНИЕМ, что два соотношения одинаковы.

5 равно 15, как 8 равно 24.

5 — это третья часть из 15, так же как 8 — это третья часть из 24.

Теперь мы введем этот символ 5:15 для обозначения отношения 5 к 15. Соотношение будет выглядеть следующим образом:

5:15 = 8:24.

«5 равно 15, как 8 равно 24.»

Проблема 1. Прочтите следующее. Почему каждая пропорция?

а) 2: 6 = 10: 30

«2 равно 6, а 10 равно 30.»Потому что 2 — это третья часть от 6, точно так же, как 10 — это третья часть от 30.

б) 12: 3 = 24: 6

«12 равно 3, как 24 — 6». Поскольку 12 четыре раза 3, так же как 24 четыре раза 6.

c) 2: 3 = 10: 15

«2 равно 3, как 10 — 15.» Поскольку 2 составляет две трети от 3, точно так же 10 составляет две трети от 15.

Задача 2. Завершите каждую пропорцию.

а) 1: 2 = 5: 10	б) 3: 9 = 10:30	в) 4: 1 = 20: 5

d) 49: 7 = 56: 8	e) 6: 42 = 9: 63	е) 18: 2 = 45: 5

г) 2: 3 = 10: 15	ч) 3: 4 = 75: 100	i) 2: 5 = 20:50

Проблема 3.

AB, CD прямые, а AB составляет три пятых CD. Выразите это соотношение в виде пропорции.

AB: CD = 3: 5

Пример 1. Если пропорционально a : b = 3: 4, то какое именно соотношение имеет a к b ?

Ответ . Пропорция подразумевает отношение a к b , но не указывает это соотношение явно.Какое соотношение имеет 3 к 4? 3 составляет три четверти из 4. Таким образом, в явном виде это соотношение a к b . a — это три четверти от b .

Пропорции подразумевают соотношений.

Проблема 4. Ясно, какое отношение имеет x к y ?

а) x : y = 1: 5.

x — пятая часть y .

б) x : y = 32: 8.

x четыре раза y .

c) x : y = 7: 10.

x составляет семь десятых от y .

Теорема об альтернативной пропорции

Числа в пропорции называются членами: 1-й, 2-й, 3-й и 4-й.

1-я: 2-я = 3-я: 4-я

Мы говорим, что 1-й и 3-й — соответствующие термины, а также 2-й и 4-й.

Следующая теорема об альтернативной пропорции:

Если четыре числа пропорциональны, то соответствующие члены
также пропорциональны.

Как первый член относится к третьему, так и второй будет к четвертому.

Если

a: b = m: n,

затем, поочередно,

a: m = b: n.

(Евклид, VII.13.)

Например, с

1: 3 = 5: 15,

, затем поочередно

1: 5 = 3: 15.

(Навык арифметики: Урок 17, вопрос 2.)

Задача 5. Назовите альтернативную пропорцию.

а)	10:30 = 5:15	б)	2: 8 = 6: 24

	10 равно 5, а 30 равно 15.		2 равно 6, как 8 равно 24.

в)	2: 3 = 10: 15

	2 равно 10, а 3 равно 15.

Это ведет к:

Теорема об одном и том же кратном

Завершим эту пропорцию,

4: 5 = 12:?

4 составляет четыре пятых от 5 (Урок 2), но не очевидно, какое число 12 составляет четыре пятых.

В качестве альтернативы, однако, 4 — это третья часть 12 — или мы могли бы сказать, что 4 было умножено на на 3. Следовательно, 5 также нужно умножить на 3 —

4: 5 = 12: 15

То есть

4: 5 = 3 × 4: 3 × 5.

Это называется теоремой об одном и том же кратном.

4 составляет четыре пятых от 5. Но каждые 4 имеют такое же отношение к каждой 5.Две четверки при их сложении будут иметь такое же отношение к двум пятеркам. Три четверки будут иметь такое же отношение к трем пятеркам. И так далее. Любое количество четверок будет иметь такое же отношение, четыре пятых, к равному количеству пятерок.

Вот как мы формулируем теорему:

Если мы умножим два числа на одно и то же число,
, то у произведений будет такое же соотношение
, что и у умноженных нами чисел.

(Евклид, VII.17.)

Задача 6. Напишите пять пар чисел с таким же соотношением, как 3: 4.

Создайте их, взяв одно и то же число, кратное 3 и 4. Например,

6: 8, 9: 12, 12: 16, 15: 20, 18: 24

Задача 7. Завершите каждую пропорцию.

а) 4: 9 = 8: 18	б) 4: 9 = 12: 27	в) 4: 9 = 16: 36

d) 7: 8 = 21: 24	e) 9: 5 = 63: 35	е) 4: 11 = 20: 55

г) 2: 9 = 16: 72	ч) 6: 5 = 54: 45	i) 8: 3 = 56: 21

Проблема 9.Завершите эту пропорцию, 2 . 45: 7 = 245:
700.

Поскольку 2,45 было умножено на 100, то 7 также нужно умножить на 100.

PQ составляет две пятых RS. Если PQ составляет 12 миль, то какова длина RS?

Решение. Поскольку PQ составляет две пятых RS, то пропорционально

PQ: RS = 2: 5.

Если PQ составляет 12 миль, то

PQ: RS = 2: 5 = 12 миль:? миль.

То есть 12 миль соответствуют PQ и 2. А поскольку 12 — это 6 × 2, пропущенный член равен 6 × 5:

PQ: RS = 2: 5 = 12 миль: 30 миль.

RS составляет 30 миль.

Или, начиная с

PQ: RS = 2: 5,

, затем обратно,

RS: PQ = 5: 2.

Итак, какое отношение имеет 5 к 2? 5 равно , умноженному на два с половиной 2.Следовательно, RS в два с половиной раза больше PQ. И если PQ составляет 12 миль, тогда RS составляет 24 + 6 = 30 миль.

Проблема 10.

AB составляет три четверти CD. В частности, AB составляет 24 см. Какова длина компакт-диска?

AB: CD = 3: 4 = 24 см:? Поскольку 24 — это 8 × 3, пропущенный член равен 8 × 4 = 32 см.

Теорема об общем делителе

Поскольку мы можем умножить оба члена на одно и то же число, тогда, симметрично, мы можем разделить оба члена на одно и то же число.

25: 40 = 5: 8

при делении 25 и 40 на 5.

Таким образом, мы видим, что 25 составляет пять восьмых из 40.

Задача 11. Какое соотношение имеет соотношение 16 к 40? Выразите это соотношение так, чтобы члены не имели общих делителей (кроме 1).

После деления обоих членов на 8, 16:40 = 2: 5.
Явно 16 равно двум пятым от 40.

Самые низкие сроки

Когда члены отношения не имеют общих делителей, кроме 1, то мы выразили их отношение с наименьшими членами.Это наименьшие члены — наименьшая пара чисел — которые имеют такое соотношение.

Задача 12. Какое соотношение явно имеют следующие? Выразите каждое соотношение с наименьшими условиями.

а) 6 является

три четверти из 8,
при делении каждого члена на 2.

б) 12 шт. две трети от 18.		c) 10 — две пятых от 25.

г) 9 шт. три восьмых из 24.		д) 6 составляет три пятых от 10.

е) 90 шт. девять десятых от 100.		г) 72 — это восемь девятых от 81.

ч) 16 шт. четыре пятых от 20.		i) 21 — это три десятых от 70.

Теорема крайностей и средств

Если четыре числа пропорциональны,

a: b = c: d,

то произведение крайностей равно произведению средств.

ad = bc.

И наоборот.

Для, если

a : b	=	c : d ,

затем при умножении a и b на d и c и d на b ,

ad : bd	=	bc : bd .

Следовательно, поочередно,

AD : BC	=	bd : bd .

Но bd равно bd . Следовательно,

ad	=	до н.э. .

Это то, что мы хотели доказать.

Рассматривая доказательство в обратном направлении, мы могли бы показать, что, наоборот, если

объявление	=	до н.э. ,
, затем
a : b	=	c : d .

Эта теорема, или, во всяком случае, ее алгебраическая версия, кажется, единственная, которая преподается в школах, и она стала механическим методом решения всех задач о соотношении.Студент должен сопротивляться этому искушению и должен понимать факты отношения и пропорции. Мы включаем его сюда только для объяснения следующего:

Пример 3. Если a и b — числа такие, что четыре a равны трем b ,

тогда какое отношение имеет a к b ?

Ответ . Три четверти.Ибо с

4	=	3 b ,
то согласно теореме крайностей и средних
a : b	=	3: 4.

a составляет три четверти от b .

Проблема 13.Если восемь m равны пяти n , то какое соотношение
имеет

м до n ?

Пять восьмых.

Язык соотношения

Пример 4. Джоан зарабатывает 1600 долларов в месяц и платит 400 долларов за аренду. Выразите этот факт на языке отношений.

Ответ . «Четверть зарплаты Джоан уходит в аренду».

Это или подобное ему предложение выражает соотношение в 400 долларов к 1600 долларов части , которая идет ей в аренду.
всего дохода.Нас интересуют не сами числа, а их соотношение.

Пример 5. В классе Эрика 30 учеников, а в классе Аны только 10. Выразите этот факт языком отношений.

Ответ . «В классе Эрика учеников в три раза больше, чем в классе Аны».

Это выражает соотношение 30 учеников к 10.

Пример 6. В классе из 24 учеников было 16 пятерок.Выразите этот факт на языке отношений.

Ответ . «Две трети класса получили четверку».

Это выражает отношение части , получившей B, к всем количеству студентов; 16 из 24. Их общий делитель равен 8. 8 делится на 16 два раз и на 24 три раз. 16 составляет две трети от 24.

Задача 14. Выразите каждое из следующих утверждений на языке соотношения.Используйте полное предложение.

а) В классе из 30 учеников было 10 пятерок.

Треть класса получила А.

б) Из 120 опрошенных 20 ответили No.

Шестая часть опрошенных ответила №

c) Население Иствилля составляет 60 000 человек, а население — 90 193 человек. D) Вествиль составляет 20 000 человек.

Население Иствилля в три раза превышает население Вествилла.

г) За лето Джон сэкономил 1000 долларов, а Боб — всего 100 долларов.

За лето Джон сэкономил в десять раз больше, чем Боб.

д) На вечеринке было 12 девочек и 4 мальчика.

На той вечеринке девочек было в три раза больше, чем мальчиков.

е) В классе из 28 учеников 21 отличник.

Три четверти учеников получили A.

г) При опросе 60 человек 40 ответили утвердительно.

Две трети опрошенных ответили утвердительно.

з) В классе из 40 учеников 25 получили «Б.»

Пять восьмых учеников получили B.

i) Из 2100 проголосовавших студентов 1400 проголосовали за Харрисона.

Две трети студентов проголосовали за Харрисона.

j) Счет в этом месяце составляет 50 долларов, а в прошлом месяце — всего 20 долларов.

Счет в этом месяце в два с половиной раза больше, чем в прошлом месяце.

k) Сабина зарабатывает 24000 долларов в год, а Клара всего 16000 долларов.

Сабина зарабатывает в полтора раза больше, чем Клара.

л) За последние тридцать лет население выросло с 20 000 до 70 000 человек.

За последние тридцать лет население выросло в три с половиной раза.

Следующая тема: Непрерывное против дискретного

Содержание | Дом

Сделайте пожертвование, чтобы TheMathPage оставался в сети.
Даже 1 доллар поможет.

Вопросы или комментарии?

Эл. Почта: [email protected]

Проверка пропорциональности | Purplemath

Перейти к основному содержанию

Демо MathHelp.ком
Присоединиться MathHelp.com
Войти

Выберите курс ниже

Стандартизированная подготовка к тестам
АККУМУЛЯТОР Math
ACT Math
АЛЕКС Математика
ASVAB Math
CBEST Math
CLEP Math
Математика FTCE
GED Math
GMAT по математике

Соотношение и пропорции — вопросы и ответы о способностях

Это раздел вопросов и ответов о способностях по соотношению и пропорции с объяснениями различных собеседований, конкурсных экзаменов и вступительных испытаний.Кандидаты, прочитав эту статью, могут найти тест на соответствие соотношению и пропорциям для предстоящих экзаменов, таких как SSC CGL, Railways и т. Д. Этот MCQ по соотношению и пропорциям содержит важные вопросы, соответствующие точному шаблону и программе предстоящих экзаменов. Убедитесь, что люди могут попробовать ответы на вопросы и ответы онлайн-теста на соотношение и пропорции для предстоящих экзаменов, чтобы проверить ваш уровень подготовки. Создав планировщик в соответствии с вашим удобством, он помогает участникам пройти онлайн-тест на соответствие соотношению и пропорциям с наивысшим баллом.

Онлайн-тест соотношения и пропорции — Детали теста на соотношение и пропорции

Название онлайн-теста	Соотношение и пропорции
Тип экзамена	Вопросы с несколькими вариантами ответов
Категория	Тест на способности
Количество вопросов	142

Соотношение и пропорция — это центральный пункт, который определяет отбор кандидатов на конкурсных экзаменах, таких как CAT, XAT и т. Д.И почти каждый экзамен на размещение в компании посвящен той же теме. Следовательно, кандидатам необходимо много работать и набрать больше среднего, чтобы пройти в финальный раунд отбора. Кандидаты проходят этот онлайн-тест на соотношение и пропорции, чтобы получить работу или пройти экзамен.

Вопросы о соотношениях и пропорциях

Практикуйте свой тест на соотношение и пропорции здесь. Мы предоставляем нашим любимым зрителям бесплатную онлайн-викторину «Соотношение и пропорции». Этот онлайн-тест «Соотношение и пропорции» посвящен количественному тесту способностей.Цель этой викторины MCQ по соотношению и пропорциям — помочь оценить знания участников о соотношении и пропорциях. Эти вопросы и ответы с несколькими вариантами выбора соотношения и пропорции подготовят участников к техническому раунду и многим сертификационным экзаменам.

Соотношение и пропорции Ответы на вопросы теста MCQ

Целью этой викторины MCQ по соотношению и пропорциям является отслеживание прогресса кандидата и понимание соотношений, ставок и пропорций. Кандидаты выбирают лучший ответ на каждый вопрос.А также покажите свою работу в Workspace в случае грубой работы. Кроме того, данные регулярно посещают нашу веб-страницу allindiaexams.in.

Словарь для академического письменного задания IELTS 1 (часть 1)

Детали: Последнее обновление: четверг, 6 декабря 2018 г. 17:07; Написано IELTS Mentor; Hits: 722369

Academic IELTS Writing Task 1 вопрос требует, чтобы вы использовали несколько словарей для представления данных, представленных в виде круговой / столбчатой / линейной / смешанной диаграммы, или для описания процесса или блок-схемы.Умение использовать соответствующие словари, представление основных тенденций, сравнение и сопоставление данных и представление логической последовательности графика обеспечивают высокий балл в вашем письменном задании Academic IELTS 1. Этот раздел словарного запаса призван помочь вам выучить все словари и фразы и слова, которые вам нужно знать и использовать в своем письменном задании 1 для академического письма, чтобы получить более высокий балл. Экзаменатор будет использовать четыре критерия для оценки вашего ответа: выполнение задания, последовательность и сплоченность, лексический ресурс, а также грамматический диапазон и точность.Поскольку лексический ресурс будет определять 25% вашей оценки в Задаче 1, вам необходимо пополнить свой словарный запас, чтобы набрать высокий балл. Чтобы продемонстрировать, что у вас отличный лексический ресурс, вам необходимо:

»Используйте правильные синонимы в своем письме.
» Используйте широкий словарный запас.
» Не повторяйте слова и фразы из экзаменационного вопроса, если нет альтернативы.
» Используйте менее распространенную лексику.
» Не используйте одно и то же слово более одного / двух раз.
» Используйте точные слова в предложении.

Желательно выучить синонимы и точно использовать их в письме, чтобы создать впечатление, что вы можете использовать хороший словарный запас.

Словарь по написанию графиков:

Общий формат для написания академического письменного задания 1 выглядит следующим образом:

Введение + основные / общие тенденции + подробное описание + сводка (необязательно) .

Каждая часть имеет определенный формат, поэтому наличие необходимого словаря поможет вам эффективно решить задачу 1 и сэкономит много времени.

Словарь для вводной части:

Начальный

Тип презентации

Глагол

0

82 Описание предоставлено / предоставлено / представлено / показано / предоставлено

диаграмма / таблица / рисунок / иллюстрация / график / диаграмма / блок-схема / изображение / презентация / круговая диаграмма / гистограмма / столбчатый график / линейный график / данные таблицы / данные / информация / графическое изображение / диаграмма процесса / карта / круговая диаграмма и таблица / гистограмма и круговая диаграмма…

показывает / представляет / изображает / перечисляет / иллюстрирует / представляет / дает / предоставляет / очерчивает / очерчивает / описывает / очерчивает / выражает / обозначает / сравнивает / показывает контраст / указывает / цифры / дает данные / дает информацию о / представляет информацию о / показывает данные о / демонстрирует / набрасывает / обобщает …

сравнение…
различий…
изменений …
количество…
информации о…
данных о…
доля…
сумма…
информации о…
данные о …
сравнительные данные …
тенденции …
проценты …
соотношение …
как …

Пример:

1. На диаграмме показаны уровни занятости среди взрослого населения в четырех европейских странах с 1925 по 1985 год.

2. Приведенные круговые диаграммы представляют соотношение мужчин и женщин, работающих в 6 широких категориях, разделенных на занятых вручную и не работающих. ручного труда в Австралии с 2010 по 2015 год.

3. На диаграмме представлена информация о потребительских расходах на шесть продуктов в четырех странах, а именно в Германии, Италии, Великобритании и Франции.

4. Прилагаемая гистограмма сравнивает количество выпускников мужского и женского пола в трех развивающихся странах, а данные таблицы представляют общий уровень грамотности в этих странах.

5. Гистограмма и данные таблицы отображают потребление воды в различных секторах в пяти регионах.

6. На столбчатой диаграмме перечислены деньги, потраченные на различные исследовательские проекты, а на столбчатой диаграмме показаны источники финансирования за десятилетие, начиная с 1981 года.

7. Линейный график показывает соотношение мужчин и женщин в трех разных секторах в Австралии в период с 2010 по 2015 год.

Обратите внимание, что некоторые учителя предпочитают «Линейный график демонстрирует …» формат вместо « данный линейный график демонстрирует …» . Однако, если вы напишете «Дано / предоставлено / представлено…» , это тоже будет правильным.

Советы:

1.Для одного графика используйте «s» после глагола, например, — дает данные, показывает / представляет и т. Д. Однако, если графиков несколько, НЕ используйте «s» после глагола.

2. Если имеется несколько графиков, и каждый из них представляет разные типы данных, вы можете написать, какой график представляет какой тип данных, и использовать «while», чтобы показать соединение. Например: «Данная гистограмма показывает сумму, потраченную на продукты быстрого питания в Великобритании в 2009 году, а круговая диаграмма представляет собой сравнение возрастов людей, которые тратили больше на продукты быстрого питания.

3. Ваше представление должно произвести впечатление, поскольку оно производит первое впечатление на экзаменатора. Это либо увеличивает, либо снижает ваш общий балл.

4. Для нескольких графиков и / или таблиц, вы можете написать, что они представляют в комбинации, вместо того, чтобы говорить, что каждый график изображает. Например, «Две круговые диаграммы и столбчатая диаграмма в комбинации отображают картину преступности в Австралии с 2005 по 2015 год и процентное соотношение молодых правонарушителей за этот период.»

Осторожно:
Никогда не копируйте слово в слово из вопроса. Если вы это сделаете, вы будете наказаны. Всегда перефразируйте введение своими словами.

Часть общего заявления:

Общее утверждение — это первое предложение (или два), которое вы пишете в своем отчете. Оно всегда должно касаться:

Что + Где + Когда.

Пример. На диаграмме представлена информация о процентном соотношении учителей, выразивших свое мнение по поводу различные проблемы, с которыми они сталкиваются при работе с детьми в трех австралийских школах с 2001 по 2005 год.

Что = процентное соотношение учителей …
Где = три австралийские школы …
Когда = с 2001 по 2005 год …

Хорошее Общее утверждение всегда должно содержать эти части.

Словарь для общей тенденции Часть:

В целом, В целом, В целом, В целом, очевидно, Как наблюдается, Как общая тенденция, Как можно видеть, Как общая тенденция, Как представлено, Это можно ясно увидеть, что, на первый взгляд, ясно, с самого начала ясно, что это видно при взгляде на графики…

Пример:

1. В целом возможности трудоустройства увеличивались до 1970 года, а затем уменьшались в течение следующего десятилетия.

2. Как видно, цифры по лишению свободы в пяти упомянутых странах не показывают общей картины, а скорее показывают значительные колебания от страны к стране.

3. В целом уровень жизни граждан в США был намного лучше, чем в остальных странах.

4. Как видно, наибольшее количество пассажиров пользовалось станцией лондонского метро в 8:00 утра и в 6:00 вечера.

4. В целом в 1987 году на руководящие должности было занято больше мужчин, чем женщин в Нью-Йорке в этом году.

5. В целом количество зарегистрированных преступлений росло довольно быстро до середины семидесятых, оставалось неизменным в течение пяти лет и, наконец, снизилось до 20 случаев в неделю после 1982 года.

6. На первый взгляд, это Ясно, что за этот период больше процентов учеников родных университетов нарушили нормы и правила, чем иностранные студенты.

7. Вначале очевидно, что пьянство в общественных местах и вождение в нетрезвом виде были наиболее частыми причинами ареста граждан США в 2014 году.

8. В целом, часы досуга, которыми пользуются мужчины, независимо от их статуса занятости , был намного выше, чем у женщин.

Структура IELTS Academic Writing Task 1 (Написание отчета):

Введение:

Введение ( никогда не копируйте слово в слово из вопроса ) + Обзор / Общая тенденция ( то, что диаграммы показывают на первый взгляд ).

Подробная информация об отчетах:

Основные функции в деталях
+ Сравнение и контраст данных. (Не приводите все цифры.)
+ Наиболее яркие черты графика.

Заключение:

Заключение (Общее заявление + Последствия, важные комментарии)
[Заключительная часть не обязательна.]

Советы:
1. Напишите введение и общую тенденцию в одном абзаце. Некоторые студенты предпочитают писать «Общие тенденции» в отдельном абзаце, а многие учителя предлагают записать и то, и другое в одном абзаце.Если у вас нет действительно веской причины написать общую тенденцию во втором абзаце, попробуйте записать их оба в первом абзаце. Однако это всего лишь предложение, а не требование.

2. Ваше «Введение» (общее заявление + общая тенденция / общая тенденция) должно состоять из 75 — 80 слов.

3. НЕ указывайте цифры, проценты или количество в общей тенденции. Скорее приведите наиболее яркую особенность графика, которую можно легко понять с первого взгляда. Таким образом, предлагается ИЗБЕГАТЬ —

«Взгляд на графики показывает, что 70% мужчин были заняты в 2001 году, в то время как 40 тысяч женщин в этом году имели работу.»

И используйте следующий формат / сравнение:

» Взгляд на графики показывает, что в 2001 году было трудоустроено больше мужчин, чем их коллег-женщин, и почти две трети женщин были безработными в том же году. «

Словарь для начала текста отчета:

Сразу после того, как вы закончите писать« Введение »(т.е. Общее заявление + Общий обзор / тенденция), вы должны начать новый абзац, чтобы описать основные характеристики диаграмм. .Этот второй абзац называется «Основной абзац / тело отчета». Вы можете иметь один основной абзац / тело отчета или до 3 (в любом случае не более 3) в зависимости от количества графиков, представленных в вопросе, и Тип этих графиков. Существуют определенные фразы, которые вы можете использовать в начале основного абзаца, и ниже приводится список таких фраз —

1. Как показано на диаграммах / графиках / круговых диаграммах ( s) / таблица …
2. Как показано на рисунке …
3.Как видно из …
4. Как видно из диаграмм …
5. Согласно …
6. Категорически говоря …
7. Возвращаясь к деталям …
8. Теперь, переходя к деталям …
9. Данные таблицы ясно показывают, что …
10. Диаграмма показывает, что …
11. Данные показывают, что …
12. График показывает цифру. ..
13. Интересно отметить, что …
14. Очевидно, что …
15. Примечательно, что …
16. Это явно наблюдается…
17. Очевидно …
18. Это ясно из данных …
19. Стоит отметить, что …
20. Совершенно ясно / ясно, что …
21. Можно ясно увидеть, что …
22. Можно ясно увидеть, что …
23. Можно было заметить, что …
24. Мы видим, что …

Словарь, чтобы показать изменения:

Тенденции	Форма глагола	Форма существительного
Увеличение	рост / рост ) / подъем / подъем / взлет / взлет / улучшение / прыжок / прыжок / движение вверх / ракета / взлет / всплеск.	подъем / повышение / восходящий тренд / рост / скачок / скачок / улучшение / подъем.
Снижение	падение / падение / падение / падение / падение / падение / уменьшение / падение / ухудшение / падение / ныряние / спуск / спуск / сползание / скольжение / переход в свободный- падать.	падение / снижение / снижение / нисходящие тенденции / нисходящая тенденция / снижение / падение / сползание / обвал / падение.
Устойчивость	без изменений / выравнивание / оставаться постоянным / оставаться устойчивым / плато / оставаться таким же / оставаться стабильным / оставаться статичным	устойчивое / плато / стабильное / статическое
Постепенное увеличение	—— ——	восходящий тренд / восходящий тренд / потолочный тренд
Постепенное снижение	—— ——	нисходящий тренд / нисходящий тренд / нисходящий тренд
Стабильность / без изменений	уровень (ed) выключен / остается (ed) постоянным / остается (ed) неизменным / остается (ed) стабильным / преобладает (ed) постоянство / p поздно / достигнуть (ed) плато / остаться (ed) равномерным / неизменным / выровнять (ed) вне / стабилизировать / остаться (ed) таким же.	Без сдачи, ровная, плато.

Примеры:

1. В конце года общий объем продаж компании увеличился на 20%.

2. Расходы офиса оставались неизменными в течение последних 6 месяцев, но прибыль выросла почти на 25%.

3. Уровень приема студентов в этот университет упал на 15%.

4. Население страны осталось практически таким же, как и 2 года назад.

5. Население этих двух городов значительно увеличилось за последние два десятилетия, и ожидается, что оно останется стабильным в течение следующих 5 лет.

Советы:
1. Используйте «улучшить» / «улучшить» для описания такой ситуации, как экономическое положение или статус занятости. Для обозначения чисел используйте другие глаголы / существительные, такие как увеличение.

2. Не используйте одно и то же слово / фразу снова и снова. Фактически, вы не должны использовать форму существительного или глагола для описания тенденции / изменения более двух раз; один раз лучше!

3.Чтобы получить высокий балл, вам необходимо использовать разнообразную лексику, а также строить предложения.

Словарь для отображения изменений на графиках:

Тип изменения	Форма наречия	Форма прилагательного
6 Rapid change резко / быстро / резко / быстро / поспешно / быстро / быстро / значительно / значительно / существенно / заметно.	драматический / быстрый / резкий / быстрый / поспешный / быстрый / быстрый / значительный / значительный / существенный / заметный.
Умеренное изменение	умеренно / постепенно / постепенно / последовательно.	умеренный / постепенный / прогрессивный / последовательный.
Постоянное изменение	Постоянно / непрерывно.	устойчиво / непрерывно.
Незначительное изменение	слегка / медленно / мягко / утомительно.	легкий / медленный / мягкий / утомительный.

Пример:

1. Экономическая инфляция в стране резко выросла на 20% в 2008 году.

2. В 2009 году произошло резкое падение промышленного производства.

3. Экономическая инфляция Спрос на новые дома резко вырос в 2002 году.

4. Население страны резко увеличилось за последнее десятилетие.

5. Цена на нефть умеренно выросла в течение последнего квартала, но, как следствие, цена повседневной необходимости быстро выросла.

Словарь для отображения частых изменений на графиках:

спады

Тип изменения

Глагольная форма вверх

Существительные формы

волна / колебание / колебание / колебание / сердцебиение

волны / колебания / колебания / колебания / сердцебиение

Пример:

1.Цена на товар колебалась в течение первых трех месяцев 2017 года.

2. На графике показаны колебания цены с 1998 по 2002 год.

3. Количество пассажиров на этой станции колеблется в течение дня и ранним утром и вечером он остается занятым.

4. Изменения в производстве автомобилей в Японии во втором квартале этого года резко возросли.

5. Количество учеников в дискуссионных клубах колебалось в разные месяцы года, и в последние три месяца этого года наблюдались быстрые взлеты и падения.

Советы:
1. 4. НЕ пытайтесь представить все данные, представленные на графике. Скорее выберите 5-7 наиболее значимых и важных тенденций / изменений и покажите их сравнения и контрасты.

2. В вопросе вас просят написать отчет и обобщить данные, представленные в виде графиков. Вот почему вам нужно показать сравнения, контрасты, показать самые высокие и самые низкие точки и наиболее яркие особенности в своем ответе, а не каждую часть данных, представленных на диаграмме (ах).

Типы изменений / различий и словарный запас, чтобы их представить:

Большое изменение / огромное различие:

Прилагательные Наречия

Подавляющее подавляющее большинство
Существенное Существенное
9870003 Огромное

000 9000 9000 Огромное 9000

Прилагательные Наречия

Значительно Значительно
Значительно Значительно

Среднее изменение / Умеренное различие:

Прилагательные Наречия

Скорее

Средне Небольшое

863

Изменение Наречия

Дробно Дробно
Погранично
Незначительно

Словарь и грамматика, относящиеся к датам, месяцам и годам:

» С 1990 по 2000 год, начиная с 1980 года, с 1995 по 2005 год, после 2012 года.
» К 1995 г., В 1998 г., В феврале, За период, В течение периода, В течение 2011 г.
» В первом полугодии, F

Заполнить: дать, пропорции, взять, отжать, вспыльчивость, усталость, строительство, получение. Объясните фразы жирным шрифтом. 1 Я просто болею и … все время сдаю экзамены!

Заполните: отдача, пропорция, взятие, напряжение, темперамент, усталость, строительство, получение. Объясните фразы жирным шрифтом.
1 Я просто болею и … все время сдаю экзамены!
2 Мне так надоело то, как я выгляжу.Это действительно … мне плохо!
3 Я теряю контроль. Я не могу … это больше!
4 Все не так плохо, как кажется, Трейси. Не вынимайте вещи из …!
Вы усердно учитесь, чтобы получить A-level *, у вас есть работа на неполный рабочий день, ваши родители находятся в середине 1) ……… развода, и вы беспокоитесь, что ваш лучший друг злится на тебя. По сути, вы чувствуете, что теряете контроль!
Звучит знакомо? Ну, вы не 2) ……….. потому что 92% британских подростков испытывают стресс. Так как давление нарастает в преддверии экзаменов, мы подумали, что расскажем вам, что такое стресс и что он делает, и, что наиболее важно, что мы можем с этим поделать!

Описание стресса
В двух словах, «стресс» — это 3)…. наши тела и разум реагируют на изменения в жизни. Не все стрессы — это плохо! В стрессовых ситуациях нервная система заставляет мышцы напрягаться, дыхание становится неглубоким, а адреналин выделяется в кровоток, когда ваше тело готовится к 4) …. вызовам с сосредоточенностью и силой. Итак, небольшой стресс может держать вас в тонусе! Но в долгосрочной перспективе это может вызвать слишком большую нагрузку на ваше сердце и вызвать другие физические и эмоциональные симптомы, такие как головные боли, депрессия, забывчивость и низкая самооценка.Однако хорошая новость заключается в том, что вы МОЖЕТЕ справиться со стрессом до того, как он выйдет из-под контроля! Итак, возьмите под свой контроль и
ПОМНИТЕ СВОИ A-B-C …
A для ДЕЙСТВИЯ
Вы можете действовать, когда стресс создается чем-то, что вы можете контролировать! Например, если у вас слишком много дел, попробуйте разбить задачи на более мелкие «куски» и заниматься одним делом за раз в порядке приоритета. Возможно, вы просто взяли на себя слишком много! Если да, дайте 5) … какое-то мероприятие после школы, например, или попросите друга или члена семьи помочь вам облегчить нагрузку.
B для BEARIT
Если вы ничего не можете сделать, вам просто нужно «улыбнуться и терпеть»! Если сначала вы не можете изменить свои чувства, научитесь контролировать свои мысли. Когда вы чувствуете себя подавленным, сделайте 6) медленный вдох и сосчитайте до десяти. Позже, когда вы успокоитесь, проанализируйте проблему рационально. Возможно, вы могли бы повторить поговорку, которая поможет вам принять вашу ситуацию, например: «Однажды я буду смеяться над этим». Кроме того, старайтесь смотреть на вещи в перспективе и не слишком драматично! Сказать, что вы «выдергиваете волосы» или что ваша нагрузка убивает, вы только ухудшите свое самочувствие!
C для COPE
Найдите способы справиться со стрессом! Для начала, сделайте что-нибудь вроде прогулки или чашечки кофе с другом, помогите взять свой 7)………. прочь от того, что тебя беспокоит. Или, возможно, стихи или ведение дневника помогут вам 8) ….. справиться с негативными эмоциями. И последнее, но не менее важное: получение достаточного количества пищи, физические упражнения и регулярное питательное питание — все это необходимо для того, чтобы справиться со стрессом! Прежде всего, постарайтесь сохранить чувство юмора и позитивный настрой! Вы не должны позволять проблемам управлять своей жизнью!
5 Джо меня так злит. Я снова потерял ………. с ней вчера.
6 Я думаю, он чувствует……….. о разводе его родителей.
7 Я не только начал чувствовать стресс. Это было ……… в течение нескольких недель.
8 Мои родители ………. мне тяжело.

Определение пропорции в Медицинском словаре

По сравнению с сельскими медсестрами в Канаде в целом большая часть сельских медсестер NB работала в домах престарелых / учреждениях долгосрочного ухода и меньшая доля работала в больницах. Доля тех, кто получил A * -A, выросла на 4,6% до 23,8%. Размеры ширины были количественно определены геометрическими пропорциями, связанными друг с другом и сравненными с золотой пропорцией, повторяющейся эстетической пропорцией зубов (RED) и золотым процентом.Необходимо провести дальнейшие исследования на более широкой популяции с различными стереотипами, чтобы доказать существование золотого процента и красной пропорции в индийском населении. Золотая пропорция была обнаружена в изделиях и конструкциях с древнеегипетских времен. В настоящее время эстетические стоматологические переменные, такие как пропорции, симметрия, гармония и доминирование (в зависимости от размера, формы и положения зубов) были пересмотрены несколькими исследователями, которые предложили модели в попытке объяснить универсальную красоту пропорций зубов.Год назад венчурные компании с показателем 11,2% отставали от компаний, занимающихся инфраструктурой и недвижимостью, по доле женщин, занимающих высшие руководящие должности. Вторая реальность является прямым следствием первой: поскольку поток сбросов у каждого поставщика варьируется в одной степени или другое, пропорция любых без исключения ингредиентов в потоке составной рецептуры обязательно изменяется в результате. Среди переменных, которые, как было установлено, положительно связаны с показателями материнства подростков на уровне почтового индекса, являются: доля разведенного сообщества; доля отделенного сообщества; доля рабочей силы, работающей в среднем 15-35 часов в неделю; доля рабочей силы, занятой в отраслях, связанных с финансами; и доля населения, живущего в бедности.

Как составить и рассчитать пропорцию: онлайн калькулятор

Онлайн калькулятор пропорций

Формула пропорций

Основные свойства пропорции

Решение пропорции с одним неизвестным | Уравнение

Как посчитать пропорцию

Пропорциональное деление. Деление на пропорциональные части

Деление числа на пропорциональные части

Деление на части, обратно пропорциональные числам

Соотношение сторон видео | Пропорции видео

Что такое пропорции видео?

Как узнать соотношение сторон видеоклипа?

Какие бывают стандартные разрешения и какие соотношения сторон для них используются?

Какое соотношение сторон рекомендуется для YouTube?

Как выявить проблемы неправильного соотношения сторон?

Как исправить пропорции видео при помощи Movavi Конвертера Видео?

Онлайн урок: Прямая и обратная пропорциональные зависимости по предмету Математика 6 класс

Как соотношение сторон фотографии влияет на композицию на примере пейзажной съемки

Пропорции человека. Для рисующих и прочих :))): 3d_tutorials — LiveJournal

Соотношение и пропорции.<img src='/800/600/http/images.myshared.ru/6/632255/slide_24.jpg' /> Эволюция реальных чисел.

Проверка пропорциональности | Purplemath

Выберите курс ниже

Соотношение и пропорции — вопросы и ответы о способностях

Онлайн-тест соотношения и пропорции — Детали теста на соотношение и пропорции

Вопросы о соотношениях и пропорциях

Соотношение и пропорции Ответы на вопросы теста MCQ

Словарь для академического письменного задания IELTS 1 (часть 1)

Словарь для академического письменного задания IELTS 1 (часть 1)

Введение + основные / общие тенденции + подробное описание + сводка (необязательно) .

Словарь для вводной части:

0

Часть общего заявления:

Словарь для общей тенденции Часть:

Структура IELTS Academic Writing Task 1 (Написание отчета):

Введение:

Подробная информация об отчетах:

Заключение:

Словарь для начала текста отчета:

Словарь, чтобы показать изменения:

Словарь для отображения изменений на графиках:

Типы изменений / различий и словарный запас, чтобы их представить:

Словарь и грамматика, относящиеся к датам, месяцам и годам:

Определение пропорции в Медицинском словаре

Добавить комментарий Отменить ответ

Соотношение и пропорции. Эволюция реальных чисел.