Абсолютная отметка дна котлована: образец, съемка, разработка и особенности проведения геодезических работ до составления плана
- Отметка — дно — траншея
- 20.2. Расчет креплений котлованов
- вычисление объема котлована, расчет выемки грунта под котлован в Москве и СПб
- Передача отметки на дно глубокого котлована — КиберПедия
- Подсчет объемов котлованов и въездных траншей — Студопедия.Нет
- БЛОК 1: Основные английские слова (Книга 1)
- Абсолютное значение в алгебре
- Абсолютный ноль — Простая английская Википедия, бесплатная энциклопедия
Отметка — дно — траншея
Отметка — дно — траншея
Cтраница 1
Отметка дна траншеи ( низа трубы) в месте установки обноски — в узловом колодце — должна быть ( по проектному профилю) SA 109, 16; отметка верхней грани: полки, определенная нивелировюй, — г2 113 262 При длине ходовой визирки hi 4 м длина постоянной визиры.
[1]
Отметка дна траншеи под фундаменты стен, расположенных по осям А, Б и 1, должна быть — 1 800, так как такую отметку имеет подошва фундамента.
[2]
Отклонения отметок дна траншеи от проектных не должны превышать 5 см на участке длиной 1 М для трубопроводов диаметром менее 1220 мм, и 10 см — для трубопроводов диаметром 1220 мм и более.
[3]
Перед укладкой труб должно быть проверено соответствие отметок дна траншеи ( или песчаной подушки) проектным данным. При несоответствии отметок дна траншеи проектным данным необходимо внести соответствующие исправления в земляные работы, что нетрудно сделать, если основанием газопровода служит песчаная постель.
При несоответствии отметок дна траншеи проектным данным необходимо внести соответствующие исправления в земляные работы, что нетрудно сделать, если основанием газопровода служит песчаная постель.
[4]
При работе системы по схеме непрерывного цикла допускается отклонение отметки дна траншеи только в сторону недобора, а при прерывистом цикле — в обе стороны.
[5]
Длина визирки вычисляется как разность отметок верха неподвижной визирки и отметки проектного дна траншеи или низа внутренней стороны трубы. Правильность рытья траншеи или укладки труб контролируют следующим образом: подвижную визирку опускают нижним концом на проверяемую точку и смотрят, находятся ли на одной линии все три визирки: подвижная и обе неподвижных. Если планка ходовой визирки выходит над линией, соединяющей постоянные визирки, то это значит, что проверяемая точка еще высока и дно траншеи необходимо углубить, а трубу опустить.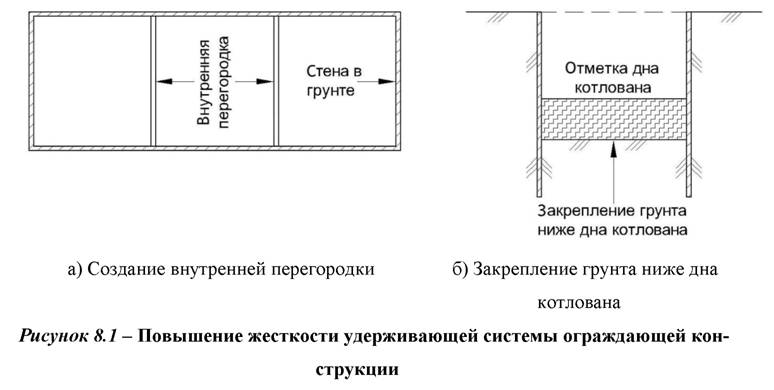
[6]
Рыхление грунта осуществляется шпуровыми зарядами на глубину промерзания грунта, если отметка дна траншеи находится ниже ее, и на глубину траншеи — в противном случае. Применение специальных навесных рыхлителей позволяет значительно повысить темп землеройных работ. Разрыхленный грунт планируется бульдозером, а разработка траншеи выполняется одноковшовым экскаватором. Протяженность разрыхляемого уча -, стка принимается равной сменной производительности одноковшового экскаватора во избежание повторного смерзания грунта.
[7]
Отметка любой точки поверхности земли от уровня моря называется черной отметкой, отметка дна траншеи над уровнем моряШв — ваетои Красно.
[8]
Режим водоотлива должен быть таким, чтобы уровень воды всегда находился ниже отметки дна траншеи. При небольшом притоке грунтовых вод колодец изготовляется в виде деревянного бездонного ящика размером 0 7 X I м или 1 X 1 м, в стенках которого просверливают отверстия, закрываемые сеткой, для стока воды. Ящик вкапывают в дно траншеи и углубляют по мере рытья траншеи, осаживая его ударами кувалды.
При небольшом притоке грунтовых вод колодец изготовляется в виде деревянного бездонного ящика размером 0 7 X I м или 1 X 1 м, в стенках которого просверливают отверстия, закрываемые сеткой, для стока воды. Ящик вкапывают в дно траншеи и углубляют по мере рытья траншеи, осаживая его ударами кувалды.
[9]
20.2. Расчет креплений котлованов
20.2.1. Расчет тонких (гибких) свободно стоящих стенок
Безанкерная тонкая подпорная стенка представляет собой в расчетном отношении статически определимую балку, имеющую опору в основании и находящуюся в статическом равновесии вследствие уравновешенного активного и пассивного давлений грунта. Задача расчета состоит в определении глубины забивки и толщины стенки.
Расчет безанкерных стенок ведется по методу Блюма-Ломейера (способ «упругой линии»), который дает результаты, вполне отвечающие натурным данным. Так как эпюра распора и эпюра отпора обычно имеют сложные очертания в связи с неоднородностью грунта, то целесообразнее вести расчет графоаналитическим способом.
Коэффициент пассивного давления грунта λp принимается по табл. 20.2 или вычисляется по формулам гл. 7.
ТАБЛИЦА 20.2. КОЭФФИЦИЕНТЫ АКТИВНОГО И ПАССИВНОГО ДАВЛЕНИЯ ГРУНТА
| φ0I | λa | λp | φ0I | λa | λp |
| 10 | 0,70 | 1,42 | 28 | 0,36 | 2,77 |
| 11 | 0,68 | 1,47 | 29 | 0,35 | 2,88 |
| 12 | 0,66 | 1,52 | 30 | 0,33 | 3,00 |
| 13 | 0,63 | 1,57 | 31 | 0,32 | 3,12 |
| 14 | 0,61 | 1,64 | 32 | 0,31 | 3,25 |
| 15 | 0,59 | 1,69 | 33 | 0,30 | 3,39 |
| 16 | 0,57 | 1,76 | 34 | 0,28 | 3,54 |
| 17 | 0,55 | 1,82 | 35 | 0,27 | 3,69 |
| 18 | 0,53 | 1,89 | 36 | 0,26 | 3,85 |
| 19 | 0,51 | 1,96 | 37 | 0,25 | 4,02 |
| 20 | 0,49 | 2,04 | 38 | 0,24 | 4,20 |
| 21 | 0,47 | 2,12 | 39 | 0,23 | 4,39 |
| 22 | 0,46 | 2,20 | 40 | 0,22 | 4,60 |
| 23 | 0,44 | 2,28 | 41 | 0,21 | 4,82 |
| 24 | 0,42 | 2,37 | 42 | 0,20 | 5,04 |
| 25 | 0,41 | 2,46 | 43 | 0,19 | 5,29 |
| 26 | 0,39 | 2,56 | 44 | 0,18 | 5,55 |
| 27 | 0,38 | 2,66 | 45 | 0,17 | 5,83 |
Первым этапом расчета является построение эпюр активного и пассивного давления грунта. Поскольку требуемая глубина забивки стенки первоначально неизвестна, эпюры строят до уровня, заведомо превосходящего ее. Далее ординаты эпюр σp и σa взаимно вычитаются и результирующую эпюру, как обычно при графоаналитических расчетах, делят на полоски (рис. 20.3, б), которые заменяют сосредоточенными силами, равными площадям полосок (рис. 20.3, в). По этим силам строят силовой (рис. 20.3, г) и веревочный (рис. 20.3, д) многоугольники. Полюс O силового многоугольника удобно принимать на одной вертикали с началом первой силы, полюсное расстояние Н не следует выбирать чрезмерно большим, так как при этом уменьшается кривизна веревочного многоугольника и в результате снижается точность расчета. Направление замыкающей веревочного многоугольника определяется первым его лучом, продленным до пересечения с последним лучом (см. пунктир на рис. 20.3, д). Полученная фигура представляет собой в определенном масштабе эпюру изгибающих моментов в стенке.
Поскольку требуемая глубина забивки стенки первоначально неизвестна, эпюры строят до уровня, заведомо превосходящего ее. Далее ординаты эпюр σp и σa взаимно вычитаются и результирующую эпюру, как обычно при графоаналитических расчетах, делят на полоски (рис. 20.3, б), которые заменяют сосредоточенными силами, равными площадям полосок (рис. 20.3, в). По этим силам строят силовой (рис. 20.3, г) и веревочный (рис. 20.3, д) многоугольники. Полюс O силового многоугольника удобно принимать на одной вертикали с началом первой силы, полюсное расстояние Н не следует выбирать чрезмерно большим, так как при этом уменьшается кривизна веревочного многоугольника и в результате снижается точность расчета. Направление замыкающей веревочного многоугольника определяется первым его лучом, продленным до пересечения с последним лучом (см. пунктир на рис. 20.3, д). Полученная фигура представляет собой в определенном масштабе эпюру изгибающих моментов в стенке. Значения моментов равны произведению полюсного расстояния в масштабе сил на соответствующие ординаты замкнутого веревочного многоугольника в масштабе длин:
Значения моментов равны произведению полюсного расстояния в масштабе сил на соответствующие ординаты замкнутого веревочного многоугольника в масштабе длин:
Mmax = Hymax.
(20.1)
В соответствии с принятой расчетной схемой точка приложения сил Е‘p и, следовательно, нижняя граница действующей эпюры пассивного давления грунта слева находятся в месте пересечения веревочного многоугольника с замыкающей на расстоянии t от поверхности грунта перед стенкой. Полная минимально необходимая глубина забивки стенки в грунте
t = t0 + Δt,
(20.2)
где Δt — длина участка стенки, необходимая для реализации обратного отпора:
,(20.3)
здесь — вертикальная нагрузка на уровне приложения силы E‘p (где hi — мощность слоя грунта с удельным весом γi).
При практических расчетах с достаточной точностью можно принимать t = 1,1t0.
Проверка общей устойчивости безанкерных стенок выполняется по методу круглоцилиндрических поверхностей скольжения, изложенному в гл. 14.
Незаанкеренные тонкие стенки обладают довольно значительной податливостью, вследствие чего в ряде случаев возникает необходимость в определении смещения их верха, которое можно представить как сумму трех слагаемых (рис. 20.4) [1]:
Δ = Δ1 + Δ2 + Δ3,
(20.4)
где Δ1 — прогиб стенки на участке свободной высоты длиной L, рассматриваемом как консольная балка; Δ2 — смещение сечения стенки, удаленного от поверхности грунта на расстояние L; Δ3 — смещение, образующееся вследствие поворота этого сечения.
Рис. 20.4. К определению деформаций безанкерной стенки
Рассматривая заглубленный участок стенки как жесткую балку, можно, используя рушения Н.К. Снитко, получить:
,(20.5)
где М и Q — соответственно изгибающий момент и перерезывающая сила в сечении стенки, удаленном на глубину L от поверхности грунта; ks — коэффициент постели грунта основания на уровне низа стенки (значение коэффициента постели изменяется по глубине).
Прогиб Δ1, при известной жесткости стенки EI легко вычисляется по табличным формулам сопротивления материалов. При трапецеидальной эпюре нагрузки на участке стенки в пределах ее свободной высоты с верхней ординатой σa1 и нижней σa2 имеем:
.(20.6)
Пример 20.1. Требуется определить необходимую глубину забивки стенки в дно котлована (до отметки 6,20 м) и изгибающий момент в стенке. Глубина котлована (свободная высота стенки) 4 м. На поверхности грунта действует временная равномерно распределенная нагрузка q = 5 кН/м2. Физические характеристики грунтов приведены на рис 20.3, а. Коэффициенты надежности по нагрузке для активного давления грунта, и для временной нагрузки γf = 1,2, для пассивного давления грунта γf = 0,8.
Решение. Вычисляем ординаты эпюры нагрузок и элементарные силы Q и сводим полученные значения в табл. 20.3 и 20.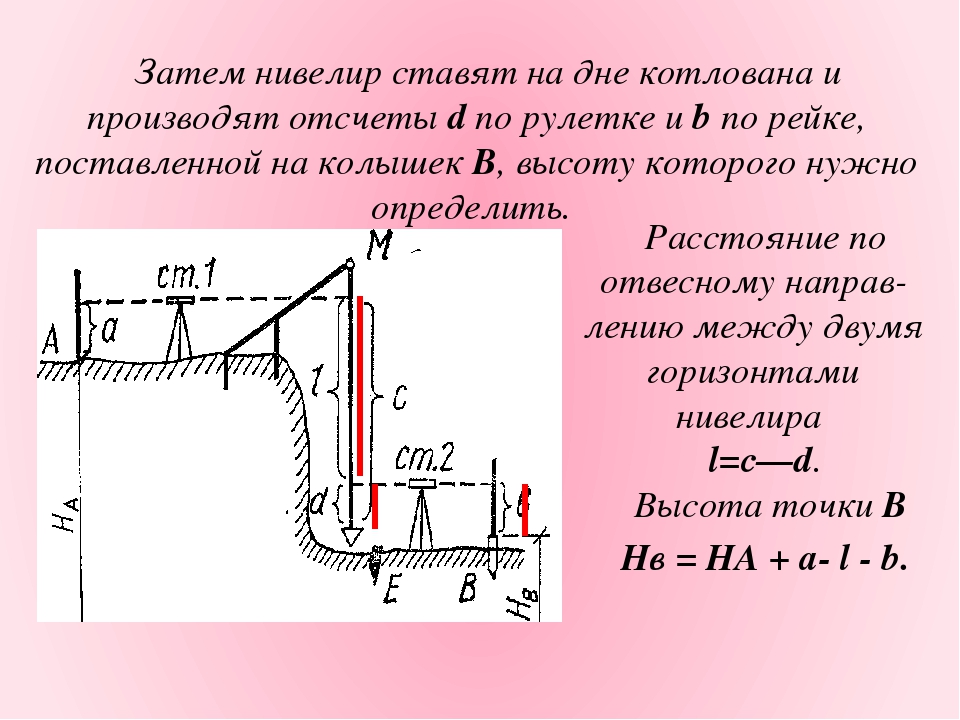 4. Выполняем графоаналитический расчет (рис. 20.3, б—д) и получаем следующие значения: t0 = 4 м; уmax = 3,8 м; Н = 50 кH; E‘p = 165 кН.
4. Выполняем графоаналитический расчет (рис. 20.3, б—д) и получаем следующие значения: t0 = 4 м; уmax = 3,8 м; Н = 50 кH; E‘p = 165 кН.
По формуле (20.3) находим:
м.
Полную необходимую глубину забивки стенки определяем по формуле (20.2):
t = 4 + 0,2 = 4,2 м.
Расчетный изгибающий момент в стенке вычисляем по выражению (20.1):
Мmax = 50 · 3,8 = 190 кН·м.
Рис. 20.3. К расчету свободно стоящей гибкой стенки (эпюра пассивного давления вычерчена слева в уменьшенном в 4 раза масштабе)
I — при γI1 = 18 кН/м3, λa1 = 0,27, φI1 = 35°; II — при γI2 = 16 кН/м3, λa2 = 0,33, φI2 = 30°; III — при γI3 = 11 кН/м3, λa3 = 0,22, φI3 = 40°
ТАБЛИЦА 20.3. РАСЧЕТ ОРДИНАТ ЭПЮРЫ НАГРУЗОК (см. рис. 20.3)
рис. 20.3)
| Отметка, м | σq = q + ΣγIiyi, кПа | λa | σa = σ’a = σqγfλa, кПа | σp = ΣγIiyi, кПа | γfλp | σ’p = σpγfγp, кПа | σa – σ’p, кПа |
| +2,00 | 5 | 0,324 | 1,6 | — | — | — | 1,6 |
| +1,00 | 5 + 4 · 18 = 23 | 0,324 | 7,5 | — | — | — | 7,5 |
| 0,00 | 23 + 1 · 18 = 41 | 0,324 0,396 | 13,3 16,2 | — | — | — | 13,3 16,2 |
| –1,00 | 41 + 1 · 16 = 56 | 0,396 | 22,2 | — | — | — | 22,2 |
| –2,00 | 56 + 1 · 16 = 72 | 0,396 0,264 | 28,5 19 | — | — | — | 28,5 19 |
| –3,00 | 72 + 1 · 11 = 83 | 0,264 | 21,9 | 1 · 11 = 11 | 3,68 | 40,5 | –18,6 |
| –4,00 | 83 + 1 · 11 = 94,9 | 0,264 | 24,8 | 22 | 3,68 | 81 | –56,2 |
| –5,00 | 94 + 1 · 11=105 | 0,264 | 27,7 | 33 | 3,68 | 121,5 | –93,8 |
| –6,00 | 105 + 1 · 11 = 116 | 0,264 | 30,6 | 44 | 3,68 | 162 | –131,4 |
Примечание. Над чертой даны значения ординат, находящихся выше отмотки, под чертой — ниже отметки.
ТАБЛИЦА 20.4. ЗНАЧЕНИЯ ЭЛЕМЕНТАРНЫХ СИЛ РАСЧЕТНОЙ СХЕМЫ НАГРУЗОК (см. рис. 20.3)
| Номер силы | Расчет | Q, кН |
| 1 2 3 4 5 6 7 8 9 | 0,5 (1,6 + 7,5) 1 0,5 (7,5 + 13,3) 1 0,5 (16,2 + 22,8)1 0,5 (22,8 + 28,5) 1 0,5 · 19 · 0,505 0,5 · 18,6 · 0,495 0, 5 (18,8 + 56,2) 1 0,5 (56,2 + 93,8) 1 0,5(93,8 + 131,4) 1 | 4,55 10,4 19,5 25,65 4,8 4,6 37,4 75 112,6 |
Приведенные выше материалы по расчету тонких свободно стоящих стенок (по Блюму—Ломейеру) основаны на пренебрежении трением между стенкой и грунтом, что является до настоящего времени общепринятым и обеспечивает необходимую глубину забивки стенки.
Будин А.Я., Демина Г.А. Набережные. Справочное пособие
вычисление объема котлована, расчет выемки грунта под котлован в Москве и СПб
Важный и неотъемлемый этап любого строительства — это создание исполнительных схем котлована. Наши геодезисты много времени тратят на этом этапе.
Наши геодезисты много времени тратят на этом этапе.
Мы максимально детально изучаем соответствие геодезических меток проектным значениям при производстве земляных работ.
Мы грамотно оформляем техническую документацию после тщательно проведенной контрольной геодезической съемки. Опыт наших геодезистов и высококлассное оборудование исключает ошибки.
Изучите эту страницу, Вы найдете массу примеров выполненных работ и узнаете подробно о том, как мы выполняем эту услугу.
Обращаясь к нам, вы получите:
- детальная разбивка контура котлована;
- контроль глубины отрывки котлована;
- расчет объема земляных работ;
- исполнительная съемка котлована;
- защита у заказчика объемов.
Посмотрите наше видео и сомнений не останется
МЫ ЛИДЕРЫ НА РЫНКЕ КАДАСТРОВЫХ И ГЕОДЕЗИЧЕСКИХ УСЛУГ
Как выполняется исполнительная съемка котлована
Исполнительную съемку котлована выполняют после зачистки его дна.
И хотя допуск на отклонения отметки достаточно значительный(5 см), такая зачистка, осуществляемая, как правило, ручным способом и позволяет уменьшить величину отклонения, влияющего на расход строительных материалов (песок, бетон) в ходе дальнейших строительных работ. Например, при проведении последующей подбетонной подготовки.
При съемке котлована определяется положение осей, размеры внутреннего и внешнего контура котлована, а также отметки дня котлована по результатам нивелирования поверхности по квадратам и их отклонениям от проектного значения.
Если проектом предусмотрено несколько значений этой отметки, то обязательно на исполнительную схему наносятся разграничительные между ними линии.
В качестве приложения могут быть приложенные расчеты по объему извлеченного грунта(картограмма земляных работ).
Как производится расчет выемки грунта под котлован
Плановая разметка выполняется тахеометром и рулеткой.
1
Вынести и закрепить на местности основные оси сооружения.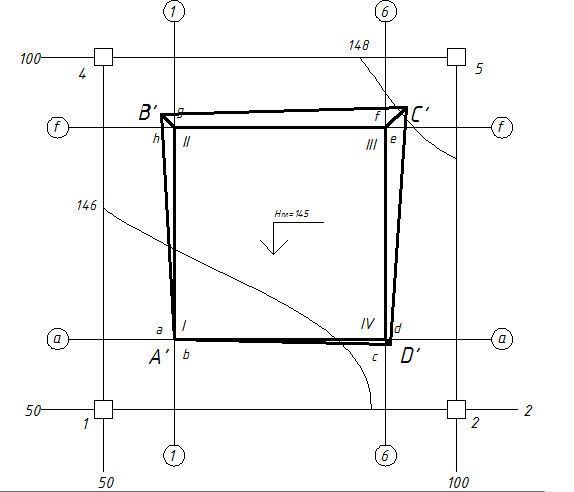
2
Отложить от основных осей здания расстояния до нижнего контура дна котлована (нижняя бровка. Данные об откладываемых расстояниях указаны в ППГР и могут быть 0,5 ÷ 1,0 м.
3
Вычислить и отложить расстояние от нижнего контура до верхнего контура котлована
В современное время выносится верхняя бровка котлована. Затем закрепляется арматурой с сигнальной лентой. При откопке арматура должна остаться.
Геодезический контроль глубины котлована с использованием визирки или нивелира, если глубина котлована до 2 м.
Последовательность работы:
- определить длину визирки
- периодически (по мере углубления) устанавливать на дно котлована переносную визирку и контролировать глубину отрывки.
Совпадение линии визирования верхней гранью визира указывает, что котлован отрыт на требуемую глубину.
Разработку глубины котлована производят экскаватором до отметки на 10 – 15 см выше проектной.
Окончательную зачистку дна котлована до проектной отметки проводят измерениями с использованием нивелира в следующей последовательности:
1
установить на дне котлована два дополнительных репера и передать на них отметку подошвы котлована от строительного репера;
2
забить колья в виде сетки 3х3 или 5х5 м по всей площади котлована;
3
установить верхний обрез кольев на проектную отметку;
4
провести контрольные измерения зачистки дна котлована по отсчетам изменений высоты установки нивелира.
Пример картограммы и исполнительной схемы котлована
Последовательность работ при разметке котлована
- На дно котлована устанавливают репер, высота которого соответствует отметке проектной глубины с небольшим завышением (до 20 см).
- На реперы 1 и 2 устанавливают нивелирные рейки. Нивелиры устанавливают наверху и внизу котлована. На кронштейне закрепляют компарированную рулетку.
- Одновременно взять отсчеты а,
- Вычислить отметку репера на дне котлована по формуле
Контроль – изменением высоты прибора на 10 – 15 см.
Расчет объема земляных работ(как посчитать объем выемки грунта), как правило, проводят по геометрическим фигурам (квадратам, трапециям, треугольникам). А наше современное время делается геодезическая съемка тахеометром, потом оформляется в программе Кредо- объемы или Civil 3d, что значительно повышает точность вычислений объемов.
Передача отметки на дно глубокого котлована — КиберПедия
Если глубина котлована менее 2 м, нивелирование производится с бровки котлована.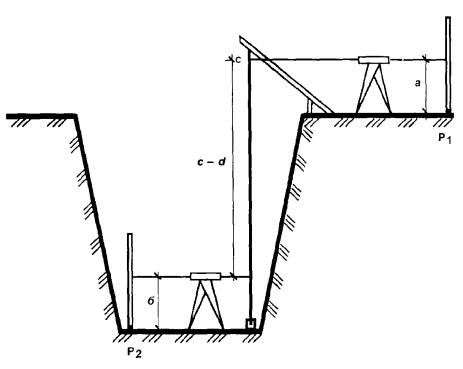 При большей глубине котлована на дне закладывают рабочий репер и передают на него отметку от реперов нивелирной сети строительной площадки. Задача решается методом геометрического нивелирования с использованием двух нивелиров одновременно, и стальной рулетки с грузом на конце, подвешиваемой на кронштейне (рис. 12).
При большей глубине котлована на дне закладывают рабочий репер и передают на него отметку от реперов нивелирной сети строительной площадки. Задача решается методом геометрического нивелирования с использованием двух нивелиров одновременно, и стальной рулетки с грузом на конце, подвешиваемой на кронштейне (рис. 12).
Рис. 12. Передача отметки на дно котлована.
С одной стороны котлована устанавливают кронштейн и подвешивают к нему прокомпарированную рулетку нулем вверх. К другому концу рулетки прикрепляют груз массой 10 кг и погружают его в ведро с вязкой жидкостью. С помощью двух нивелиров, вверху и внизу котлована, берут одновременно отсчеты в1 и в2 по рулетке и затем отсчеты а и с по рейкам, стоящим на реперах вверху и на дне котлована. Отметку репера на дне котлована вычисляют по формуле:
Нрп2=Нрп1+а-(в2-в1)-с (11)
Контроль правильности передачи отметки осуществляется путем определения отметки нижнего репера повторно. Расхождение в отметках репера №2 не должны быть более 4 мм. Берется среднее значение.
Расхождение в отметках репера №2 не должны быть более 4 мм. Берется среднее значение.
Если разность температур при компарировании рулетки и передаче отметки на дно котлована более 8°, в измеренную разность отсчетов по рулетке (в1 и в2) следует вводить поправку за температурное расширение:
∆c=α(в2-в1)(t-t0), (12)
где α=12 · 10-6 м/град – коэффициент температурного расширения стали.
Передача отметки на верхние этажи здания (монтажные горизонты)
Задача решается аналогично вышеприведенной, только в формуле (2.1) разность отсчетов по рулетке (в1 — в2) будет иметь знак «+», то есть (см. рис. 13):
Нрп2=Нпр1+а+(в2-в1)-с (13)
Рис. 13. Передача отметки на верхние этажи.
ОФОРМЛЕНИЕ БРИГАДНОГО ОТЧЕТА ПО ПРАКТИКЕ И СДАЧЕ РЕЙТИНГА И ЭКЗАМЕНА
После выполнения всех полевых и камеральных работ любая бригада составляет отчет по практике.
Все полевые и камеральные документы обязаны быть надлежащим образом оформлены и подшиты в папке-скоросшивателе в следующей последовательности:
1. Пояснительная записка.
2. Полевые и камеральные материалы по видам работ с подписями: кто оформил, составил либо вычислял. Главные чертежи вычерчивать тушью соответствующего цвета. Каждый полевой документ обязан быть пронумерован и в конце подписан бригадиром.
Примерный список вопросов, подлежащих освещению в пояснительной записке:
1. Место и время практики и кто проводит практику.
2. Виды и объемы работ и время отведенное на их по плану и практически.
3. Применявшиеся инструменты, результаты поверок.
4. Выполненные геодезические работы. Методы их выполнения и их обработка.
5. Результаты работ (их точность и сравнение с допусками).
6. Положительные и отрицательные стороны практики.
После представления отчета и его защиты преподаватель выставляет оценку в рейтинговую ведомость, тем самым дает допуск на экзамен. Компьютерный экзамен по практике сдается в конце всех практик по курсу. Тесты выдается преподавателем, либо можно скачать с сайта https://sites.google.com/site/omirzanovaz/.
Компьютерный экзамен по практике сдается в конце всех практик по курсу. Тесты выдается преподавателем, либо можно скачать с сайта https://sites.google.com/site/omirzanovaz/.
Использованная литература 1. Методические указания по геодезической практике. Специальность 290300-ПГС. Часть 1. – Балаково, 2007.http://old.bittu.org.ru/files/muarhto2011/43.pdf2. ЗемироваА.Т. Инженерная геодезия: Методические указания к учебной геодезической практике. – Оренбург: ГОУОГУ, 2006. – 116 с. http://kf.osu.ru/old/bibl/lib_books/doc_gsh/18.pdf2. Гиршберг М.А. Геодезия. – М.: Недра, 1967. – 383 с. СОДЕРЖАНИЕ
| 1 | Общие сведения о практике | 3 |
| 1.1 | Цель и задачи практики | 3 |
| 1.2 | Организация учебной практики | 3 |
| 2. | Поверки и юстировки теодолита | 4 |
| 3 | Создание плановой основы | 6 |
| 4 | Создание высотной основы | 13 |
4. 1 1 | Общий осмотр нивелира и реек | 13 |
| 4.2 | Поверки нивелира | 13 |
| 4.3 | Определение разности нулей реек | 13 |
| 4.4 | Измерение превышения | 14 |
| 5 | Тахеометрическая съемка | 16 |
| 6 | Нивелирование по квадратам | 19 |
| 7 | Решение типовых инженерно-геодезических задач | 20 |
| 7.1 | Вынос отметки на местность | 20 |
| 7.2 | Определение крена столбов (колонн) | 21 |
| 7.3 | Определение высоты предмета | 21 |
| 7.4 | Определение крена сооружения башенного типа (дымовая труба, металлическая опора ЛЭП-1000) | 22 |
| 7.5 | Разбивка основных осей здания с точек планового обоснования (с пунктов теодолитного хода) способом полярных координат | 25 |
| 7.6 | Передача отметки на дно глубокого котлована | 26 |
| 7.7 | Передача отметки на верхние этажи здания (монтажные горизонты) | 27 |
| 8 | Оформление бригадного отчета по практике и сдаче рейтинга и экзамена | 28 |
| Использованная литература | 29 |
Методическое издание Жанат Токтарбаевна Омиржанова
Методические указания по летней геодезической
практике для студентов всех специальностей
Редактор : Есимханова А.Е. Сводный план 2012-13 уч. года, поз. № 55. Формат 60х84 1/1,9. Бумага офсетная. Riso.Усл. печ.л. 2,1. Уч.-изд.л. 2,1. Тираж 100 экз.Заказ №Цена договорная. Издание Казахской головной архитектурно-строительной академииОтпечатано в Издательском доме «Строительство и архитектура»050043, г. Алматы, ул. Рыскулбекова, 28
Подсчет объемов котлованов и въездных траншей — Студопедия.Нет
Объем прямоугольного в плане котлована, расположенного на спланированной площадке с уклоном до 10%, можно определить по формуле:
V = (3.1)
где Hk – средняя глубина котлована, равная разности между планировочной отметкой в зоне котлована и отметкой дна котлована, м;
a и b – размеры котлована по дну, м;
c и d – размеры котлована по верху с учетом принятых откосов, (рис. 3.1):
c=a+2·m·Hk (3.2)
d=b+2·m·Hk (3.3)
m – показатель откоса котлована, (табл. П.2).
При сложной конфигурации в плане котлованов их следует разбить на отдельные простые геометрические тела, объемы которых подсчитывают раздельно, используя формулы объемов различных геометрических тел. Сразу же следует наметить расположение съезда в котлован, необходимого для ввода в забой экскаватора – прямая лопата, а также для работы транспортных средств. Ширина съездов принимается: при одностороннем движении транспорта – 4,0 м, при двустороннем – 6,0 м.
Объем въездной траншеи (рис. 3.2) определяется по формуле:
V = , (3.4)
где H – глубина котлована в месте примыкания траншеи, м;
b – ширина траншеи по дну, м;
m – показатель откоса котлована;
m/ – показатель откоса дна траншеи (уклон траншеи), принимается в размере 1:8¸1:12 в зависимости от вида грунта, его влажности, вида транспортных средств.
Подсчет объемов траншей
По заданию следует разработать траншею для коммуникаций. В летних условиях ее следует разрабатывать в отвал, без вывозки грунта. Ее объем может быть подсчитан по формуле:
Vmр= (b + m ·h) ·l, (3.7)
где b – ширина траншеи по низу, м;
l – длина траншеи, м;
h – глубина, м;
m – показатель крутизны откоса.
Продольный уклон дна траншеи условно принимается равным уклону спланированной поверхности.
Подсчет объемов недобора грунта
При определении объемов котлованов и траншеи следует иметь в виду, что эти сооружения должны быть вырыты без нарушения структуры грунта в основании. В связи с этим требованием при работе экскаватора предусматривается недобор грунта (табл. 3.1).
Таблица 3.1
Допускаемые недоборы грунта в основании, см, при работе одноковшовыми экскаваторами
Рабочее оборудование
экскаватора
| Емкость ковша экскаватора в м3
| ||||
| 0,25-0,4 | 0,5-0,65 | 0,8-1,25 | 1,5-2,5 | 3-5 | |
Лопата:
прямая
обратная
Драглайн
| |||||
| 5 | 10 | 20 | 15 | 20 | |
| 15 | 15 | 20 | - | - | |
| 15 | 20 | 25 | 30 | 30 | |
Объем подчистки дна котлована после отрывки его экскаватором
, (3.8)
где Fк – площадь дна котлована, м2;
hн – глубина (толщина) недобора, м, (табл. 3.1).
Объем подчистки дна траншеи после отрывки её экскаватором
, (3.9)
где Fтр – площадь дна траншеи, м2.
Поскольку выбор комплекта механизмов на данной стадии выполнения курсовой работы еще не произведен, величину слоя недобора hн можно принять равной 0,15–0,20 м с последующим уточнением.
При больших размерах котлована рекомендуется подчистку дна вести механизированными способами, используя для этой цели малые модели экскаваторов, бульдозеров, специальных планировщиков.
В траншеях срезка всего объема недобора может производиться вручную.
ВЫБОР СПОСОБОВ ПРОИЗВОДСТВА РАБОТ И КОМПЛЕКТОВ МАШИН ДЛЯ ПЛАНИРОВКИ ПЛОЩАДКИ
БЛОК 1: Основные английские слова (Книга 1)
Выучите следующие целевые слова.
Ваш пользовательский агент не поддерживает элемент HTML5 Audio.
страшно прил.
Когда кто-то боится , он испытывает страх.
Женщина была боялась увиденного.
согласен v.
К согласен означает сказать «да» или думать так же.
A: Еда в этом ресторане очень хорошая.
B: I согласен с вами .
злой прил.
Когда кто-то злится , он может захотеть громко говорить или драться.
Она не делала уроки, поэтому ее отец злой .
прибыть v.
К прибыть означает добраться или добраться до какого-то места.
Автобус всегда прибывает на углу моей улицы в 4:00.
атака v.
Атака — это попытаться драться или нанести вред.
Человек с мечом напал другого мужчину первым.
нижний н.
Нижняя часть — самая нижняя часть.
В нижней части моей обуви есть отверстие.
умный прил.
Когда кто-то умен , он может решить сложную головоломку или задачу.
Тот умный Мальчик придумал хорошую идею.
жестокий прил.
Когда кто-то жесток , он делает плохие вещи, чтобы причинить боль другим.
Мужчина жестокий кричал на сестру.
наконец нареч.
Если что-то случится , наконец, , то это произойдет через долгое время или в конце.
He наконец пересек финишную черту после пяти часов бега.
hide v.
To hide — это стараться не позволять другим видеть вас.
Остальные дети будут прятаться , пока вы считаете до 100.
охота v.
До охота — это поиск или поиск животного, которое нужно убить.
Давно люди охотились луками и стрелами.
лот н.
Лот означает большое количество или количество людей, животных, вещей и т. Д.
В корзине есть лот яблок.
средний n.
середина чего-либо — это центр или полпути.
Канадский флаг имеет кленовый лист в середине .
момент н.
Момент — секунда или очень короткий промежуток времени.
Я был всего несколько моментов опоздал на встречу.
доволен прил.
Когда кому-то нравится, , они счастливы.
Она была довольна полученным телефонным звонком.
обещание v.
Обещание означает, что вы обязательно что-то сделаете.
He обещал вернуть мой ключ к завтрашнему дню.
ответить v.
На ответ должен дать ответ или ответить кому-то.
Она спросила его, во сколько у него встреча. Он ответил , «в три».
сейф прил.
Когда человек находится в безопасности , он не в опасности.
Пристегните ремень безопасности в автомобиле безопасным .
трюк н.
Уловка — это то, что вы делаете, чтобы обмануть другого человека.
Его карта фокус нас очень удивил.
скв. нар.
Вы используете колодец , чтобы сказать, что что-то было сделано хорошо.
Пара вполне может танцевать хорошо .
Прочтите историю вслух. Обратите внимание на слова, выделенные жирным шрифтом.
Ваш пользовательский агент не поддерживает элемент HTML5 Audio.
Лев и кролик
В лесу жил жестокий лев. Каждый день он убивал и ел множество животных.Остальные животные боялись, что лев убьет их всех.
Животные сказали льву: «Давай заключим сделку. Если вы обещаете есть только одно животное каждый день, то один из нас будет приходить к вам каждый день. Тогда тебе не нужно охотиться на и убивать нас ».
План показался льву хорошо продуманным, поэтому он согласился , но он также сказал: «Если вы не будете приходить каждый день,
, я обещаю убить вас всех на следующий день!»
Каждый день после этого одно животное подходило ко льву, чтобы лев мог его съесть.Тогда все остальные животные были в безопасности.
Наконец, , настала очередь кролика идти к льву. В тот день кролик двигался очень медленно, поэтому лев был зол , когда кролик, наконец, прибыл .
Лев сердито спросил кролика: «Почему ты опоздал?»
«Я прятал от другого льва в лесу. Этот лев сказал, что он король, поэтому я испугался ».
Лев сказал кролику: «Я здесь единственный король! Отведи меня к тому другому льву, и я убью его.
Кролик ответил : «Я буду рад показать вам, где он живет».
Кролик привел льва к старому колодцу в середине леса. Колодец был очень глубоким с водой на дне . Кролик сказал льву: «Загляни туда. Внизу живет лев ».
Когда лев заглянул в колодец, он увидел свое собственное лицо в воде. Он подумал, что это был другой лев. Не дожидаясь еще , момент , лев прыгнул в колодец , чтобы атаковать другого льва.Он так и не вышел.
Все остальные животные в лесу были очень довольны умным трюком кролика .
Абсолютное значение в алгебре
Абсолютное значение означает …
… насколько число от нуля:
«6» — это 6 от нуля,
и «−6» — , а также 6 от нуля.
Таким образом, абсолютное значение 6 равно 6 ,
, а абсолютное значение −6 также равно 6
Символ абсолютного значения
Чтобы показать, что нам нужно абсолютное значение, мы помещаем «|» отмечает обе стороны (называемые «стержнями»), как в этих примерах:
| Символ «|» находится чуть выше клавиши ввода на большинстве клавиатур. |
Более формальный
Формально:
Что говорит о том, что абсолютное значение x равно:
- x, когда x больше нуля
- 0, когда x равно 0
- -x, когда x меньше нуля (это «переворачивает» число обратно в положительное значение)
Итак, когда число положительное или нулевое, мы оставляем его в покое, когда оно отрицательное, мы меняем его на положительное с помощью −x.
Пример: что такое | −17 | ?
Ну, это меньше нуля, поэтому нам нужно вычислить «−x»:
— (−17) = + 17
(Потому что два минуса составляют плюс)
Полезные свойства
Вот некоторые свойства абсолютных значений, которые могут быть полезны:
- | a | ≥ 0 всегда!
В этом есть смысл… | а | никогда не может быть меньше нуля.
- | а | = √ ( 2 )
Возведение a в квадрат делает его положительным или нулевым (для a как действительного числа). Тогда извлечение квадратного корня «отменит» возведение в квадрат, но оставит его положительным или нулевым.
- | а × б | = | а | × | b |
Значит это то же самое:
- абсолютное значение (a, умноженное на b), и
- (абсолютное значение a) раз (абсолютное значение b)
Что также может быть полезно при решении
- | u | = a то же самое, что и u = ± a, и наоборот
Что часто является ключом к решению большинства вопросов абсолютной ценности.
Пример: Решить | x + 2 | = 5
Использование «| u | = a то же самое, что и u = ± a «:
это: | x + 2 | = 5
то же самое, что и это: x + 2 = ± 5
Имеет два решения:
| х + 2 = -5 | х + 2 = +5 |
| х = −7 | х = 3 |
Графически
Давайте изобразим этот пример:
| x + 2 | = 5
Строить график легче, когда у нас есть уравнение «= 0», поэтому вычтем 5 с обеих сторон:
| x + 2 | — 5 = 0
Итак, теперь мы можем построить график y = | x + 2 | −5 и найти, где оно равно нулю.
Вот график y = | x + 2 | −5, но ради удовольствия давайте построим график , сдвинув его примерно на :
| Начать с y = | x | | , затем сдвиньте его влево, чтобы получить , это y = | x + 2 | | , затем сдвиньте его вниз, чтобы получить , это y = | x + 2 | −5 |
И два решения (в кружке): −7 и +3.
Неравенства абсолютных значений
Смешивание абсолютных ценностей и неравенств требует осторожности!
Есть 4 неравенства:
| < | ≤ | > | ≥ | |
|---|---|---|---|---|
| менее | меньше чем или равно | больше | больше чем или равно |
меньше, меньше или равно
С «<» и «≤» мы получаем один интервал с центром в нуле:
Пример: Решить | x | <3
Это означает, что расстояние от x до нуля должно быть меньше 3:
.
Все, что находится между (но не включая) -3 и 3
Его можно переписать как:
−3 <х <3
В качестве интервала можно записать:
(-3, 3)
То же самое работает для «Меньше или равно»:
Пример: Решить | x | ≤ 3
Все, что находится между , включая -3 и 3
Его можно переписать как:
−3 ≤ х ≤ 3
В качестве интервала можно записать:
[−3, 3]
Как насчет более крупного примера?
Пример: Решить | 3x-6 | ≤ 12
Записать как:
−12 ≤ 3x − 6 ≤ 12
Добавить 6:
−6 ≤ 3x ≤ 18
Наконец, умножьте на (1/3).Поскольку мы умножаем на положительное число, неравенства не изменятся:
−2 ≤ х ≤ 6
Готово!
В качестве интервала можно записать:
[−2, 6]
Больше, больше или равно
Это другое … мы получаем два отдельных интервала :
Пример: Решить | x | > 3
Это выглядит так:
до -3 или с 3 и более
Его можно переписать как
x <−3 или x> 3
В качестве интервала можно записать:
(−∞, −3) U (3, + ∞)
Осторожно! Не записывать как
−3> х> 3
«x» не может быть меньше -3 и больше 3 одновременно
Это действительно:
x <−3 или x> 3
«x» меньше −3 или больше 3
То же самое работает для «Больше или равно»:
Пример: Решить | x | ≥ 3
Можно переписать как
x ≤ −3 или x ≥ 3
В качестве интервала можно записать:
(−∞, −3] U [3, + ∞)
Абсолютный ноль — Простая английская Википедия, бесплатная энциклопедия
Нулевой кельвин (−273.15 ° C) определяется как абсолютный ноль.
Абсолютный ноль — это температура, при которой частицы вещества (молекулы и атомы) находятся в точках с наименьшей энергией. Некоторые думают, что при абсолютном нуле частицы теряют всю энергию и перестают двигаться. Это не так. В квантовой физике есть нечто, называемое энергией нулевой точки, что означает, что даже после того, как вся энергия частиц была удалена, частицы все еще имеют некоторую энергию. Это связано с принципом неопределенности Гейзенберга, согласно которому чем больше известно о положении частицы, тем меньше известно о ее импульсе, и наоборот.Следовательно, частицу нельзя полностью остановить, потому что тогда будут известны ее точное положение и импульс.
Некоторые люди создали температуры, очень близкие к абсолютному нулю: рекордная температура была на 100 пК (сто пикокельвинов, равных 10 −10 кельвинов) выше абсолютного нуля. [1] Даже приблизиться к абсолютному нулю сложно, потому что все, что касается объекта, охлаждаемого около абсолютного нуля, будет выделять тепло для этих объектов. Ученые используют лазеры для замедления атомов при охлаждении объектов до очень низких температур. [2]
Температурные шкалы Кельвина и Ренкина определены таким образом, что абсолютный ноль равен 0 кельвину (K) или 0 градусов Ренкина (° R). Шкалы Цельсия и Фаренгейта определены так, что абсолютный ноль равен -273,15 ° C или -459,67 ° F. [3]
На этом этапе давление частиц равно нулю. Если мы построим для него график, то увидим, что температура частиц равна нулю. Температура не может понизиться дальше. Кроме того, частицы не могут двигаться «в обратном направлении», потому что, поскольку движение частиц является вибрацией, вибрация в обратном направлении будет не чем иным, как просто повторной вибрацией.Чем ближе температура объекта к абсолютному нулю, тем менее резистентен материал по отношению к электричеству, поэтому он будет почти идеально проводить электричество без измеримого сопротивления.
Третий закон термодинамики гласит, что ничто не может иметь температуру абсолютного нуля.
Второй закон термодинамики гласит, что все двигатели, работающие от тепла (например, автомобильные двигатели и двигатели паровых поездов), должны выделять отработанное тепло и не могут быть на 100% эффективными.Это связано с тем, что КПД (процент энергии, потребляемой двигателем, которая фактически используется для работы двигателя) составляет 100% × (1-T вне / T внутри ), что составляет 100% только при температуре наружного воздуха. является абсолютным нулем, чего не может быть. Таким образом, двигатель не может быть эффективен на 100%, но вы можете сделать его КПД ближе к 100%, сделав более высокую внутреннюю температуру и / или более низкую внешнюю температуру.
.
