Балки это: Недопустимое название — Викисловарь
- Балки перекрытия — полезные статьи о деревянном доме
- Металлические балки
- Справочник строительных материалов и терминов (Б)
- Двухпролетные балки — Доктор Лом
- Не удается найти страницу | Autodesk Knowledge Network
- Что это за балки такие и какими разными они бывают | sevprostor
- Металлические балки
- Beams | Компания-разработчик программного обеспечения Дубай
- Перемещение лучей при нормальном падении посредством управления геометрическими фазами импульс-пространство
- Ионные пучки из плазмы: от космоса до нанотехнологий
- Криштиану Роналду сияет: «Я всегда счастлив, когда возвращаюсь в свою страну», когда звезда сборной Португалии уходит от проблем «Манчестер Юнайтед».
- определение балок по The Free Dictionary
- 9
- Лучшие бревна 2022 года
- Подъемные балки и траверсы от Fyns Kran Udstyr
Балки перекрытия — полезные статьи о деревянном доме
Балки перекрытия — это элемент несущей конструкции любого здания, в том числе деревянного дома, бани. На них ложится несущая нагрузка верхнего этажа, либо чердака, либо стропил крыши. В связи с этим к ним применяются определенные стандарты качества.
Некоторые примеры таких требований можно привести таблицей расчетов:
| Сечение балок при длине пролета, м. | |||||||
|---|---|---|---|---|---|---|---|
| Нагрузка кг/погонный метр | 3,0 | 3,5 | 4,0 | 4,5 | 5,0 | 5,5 | 6,0 |
| 150 | 5×14 | 5×16 | 6×18 | 8×18 | 8×20 | 10×20 | 10×22 |
| 200 | 5×16 | 5×18 | 7×18 | 7×20 | 10×20 | 12×22 | 14×22 |
| 250 | 6×16 | 6×18 | 7×20 | 10×20 | 12×20 | 14×22 | 16×22 |
| 350 | 7×16 | 7×18 | 8×20 | 10×22 | 12×22 | 16×22 | 20×22 |
С деревянными балочными перекрытиями часто возводят индивидуальные и малоэтажные жилые дома, деревянные коттеджи и дачи.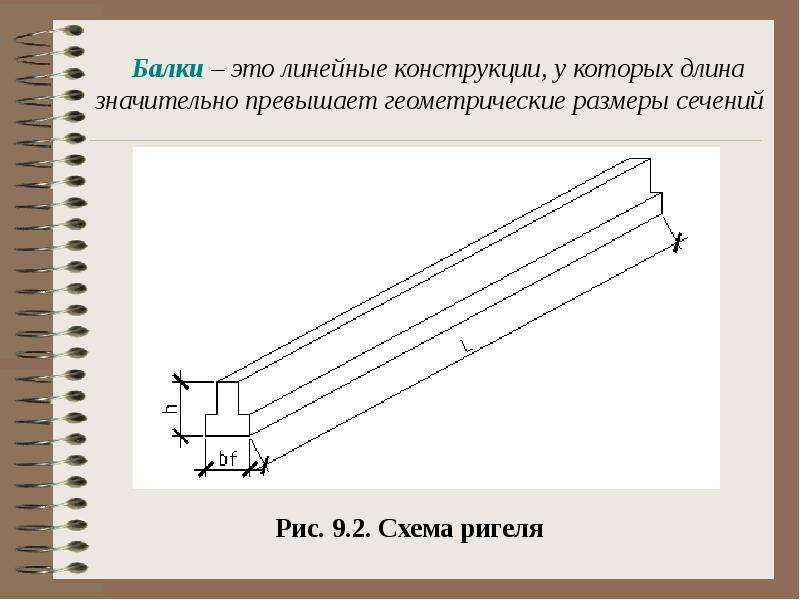 Перекрытия состоят из несущей деревянной балки, пола, меж балочного заполнения, и отдельного слоя (потолка).
Перекрытия состоят из несущей деревянной балки, пола, меж балочного заполнения, и отдельного слоя (потолка).
Как правило, балки укладываются с интервалом — 0,6 — 1 м. Это зависит от конструкции перекрытия. Для перекрытий полов на балки могут устанавливаться лаги, а уже на лаги настилаться пол, в этом случае рекомендуется что бы расстояние между ними не превышало 1 метр. Если дощатый пол (из досок толщиной до 28 мм) настилается прямо на балки перекрытия, то расстояние между ними должно быть около 0,5 м. Деревянными балками, как правило, перекрывают пролеты до 4 — 4,5 м. Опять же эти пролеты могут меняться в зависимости от ширины сечения.
В нашей компании «Северный дом» специалисты выполняют работы по изготовлению и установке несущих элементов конструкции с соблюдением всех требований к таким конструкциям. Вы можете быть уверены в качестве работ. Мы устанавливаем балки со значительным превышением расчетных параметров, что делает изготавливаемые нами конструкции деревянных домов повышенно прочными и устойчивыми. Мы изготавливаем их из круглого бревна или бруса увеличенного сечения. Помимо оригинального внешнего вида, массивные перекрытия надежно выполняют свою роль надежной несущей конструкции.
Мы изготавливаем их из круглого бревна или бруса увеличенного сечения. Помимо оригинального внешнего вида, массивные перекрытия надежно выполняют свою роль надежной несущей конструкции.
Металлические балки
Это изделия из стали и конструктивный элемент металлоконструкций в виде бруса, который расположен горизонтально или наклонен. Она является важным элементом металлоконструкций и к ее качеству предъявляются повышенные требования. Этот элемент преимущественно работает на изгиб, и поэтому очень часто именно от него зависит устойчивость и долговечность конструкции.
Изделия производятся из углеродистой или низкоуглеродистой стали. Конструкции такого типа в основном применяются в промышленном строительстве для сооружения перекрытий, опор, мостов.
При проектировании и строительстве зданий горизонтальные конструкции должны выдерживать вертикальные и поперечные весовые нагрузки. Балка, нагруженная ими, оказывает давление на колонны, подвесы, стены и перекладины. При конструкции в виде фермы стержни покоятся на балке, расположенной горизонтально.
Балка, нагруженная ими, оказывает давление на колонны, подвесы, стены и перекладины. При конструкции в виде фермы стержни покоятся на балке, расположенной горизонтально.
Основные преимущества:
- способность выдерживать большие нагрузки и при этом уменьшать их воздействие на несущие элементы;
- пожаробезопасность, стойкость к воздействию химических веществ, что обуславливает долгий срок их службы;
- устойчивость к воздействию негативных факторов окружающей среды;
- простота конструкции, благодаря которой производство, монтаж и обслуживание удобны и не требуют больших материальных и трудовых затрат;
- возможность подобрать необходимое сечение, которое может отсутствовать среди стандартных профилей металлопроката, производимого большинством предприятий;
- снижение массы и металлоемкости каркаса быстровозводимого здания из металлоконструкций за счет подборка профиля, обладающего оптимальным сечением;
- технология производства металлических балок позволяет применять разные типы сортов стали для изготовления стенок и полок, а также изготовления сечений несимметричной конфигурации.

Применение технологии
Металлические балки – конструктивный элемент быстровозводимых зданий: промышленных объектов, цехов, жилых и общественных сооружений. Они применяются при строительстве мостов, дорожных объектов и эстакад, подвесных путей. При таком использовании элемент позволяет придать большую надежность всей конструкции при уменьшении веса и позволяет экономить.
Основные виды
Сооружения можно классифицировать по толщине полок и стенок, а также по конфигурации граней полок: с уклоном, без уклона, расположенные параллельно. Также балки могут быть разделены по способу производства и области применения.
По маркировке изделия разделяют на следующие классы с соответствующими обозначениями:
- Б – нормальные;
- К – колонные;
- Ш – широкополочные;
- М – мостовые;
- С – специальные, для строительства перекрытий.
Одной из самых распространенных разновидностей элементов этого типа являются стальные горячекатаные балки с гранями полок, расположенных параллельно друг другу. Изготовленные балки должны строго соответствовать параметрам, изложенным в ГОСТ 26020–83. Длина таких элементов может составлять от 6 до 24 м. Конфигурация балок может быть нормальной, широкополочной или колонной.
Изготовленные балки должны строго соответствовать параметрам, изложенным в ГОСТ 26020–83. Длина таких элементов может составлять от 6 до 24 м. Конфигурация балок может быть нормальной, широкополочной или колонной.
При сборке металлоконструкций балка может занимать наклонное или горизонтальное положение, а также работать на изгиб, если необходимо, чтобы сооружение выдерживало значительные нагрузки.
При производстве используется специальное оборудование и технологии обработки металлоконструкицй: автоматические линии резки металла, сборки и сварки готовых конструкций. Благодаря этому готовые элементы в точности соответствуют всем необходимым стандартам и обладают необходимой прочностью, надежностью и безопасностью. Далее заготовки обрабатываются и очищаются от ржавчины и грязи. Делается это для того, чтобы защитить металл от коррозии и вредного воздействия окружающей среды. Кроме того, такая обработка позволяет максимально качественно нанести лакокрасочное покрытие, которое будет держаться на поверхности металла долгое время.
Наиболее экономически выгодными считаются сварные двутавровые балки (двутавры). При возведении объекта их требуется сравнительно небольшое количество. Таким образом, достигается экономия денежных средств.
Справочник строительных материалов и терминов (Б)
Балкой
называют конструктивный элемент, представленный горизонтальным либо наклонным
брусом, который работает в основном на изгиб.
Обычно на практике горизонтально размещенная балка воспринимает поперечную
вертикальную весовую нагрузку. Однако в ряде случаев требуется учитывать
воздействие и возможных поперечных горизонтальных сил (к примеру, ветровую
нагрузку либо при принятии во внимание вероятного землетрясения). В свою
очередь, нагруженная балка воздействует на опоры, в качестве которых могут
выступать стены, колонны, подвесы, перекладины (другие балки). Потом нагрузка
передается дальше и в результате, как правило, воспринимается конструктивными
элементами, которые работают на сжатие – опоры. Случай ферменной конструкции
Случай ферменной конструкции
выделяют отдельно, поскольку в этой конструкции стержни покоятся на балке
горизонтальной.
Прочностные свойства балки зависят от ряда ее характеристик:
— площади и формы ее поперечного сечения,
— длины балки,
— материала, из которого изготовлена балка,
— способа закрепления балки.
В современных постройках обычно применяют деревянные, стальные либо
железобетонные балки. Наиболее распространенным типом поперечного сечения
стальных балок является двутавровое сечение. Подобные двутавровые балки
применяют при возведении каркасов мостов и зданий. Также широко используют
тавровые балки, балки, изготовленные с полым профилем (например, трубы),
швеллера, балки, изготовленные с угловым профилем сечения.
Балки для опалубки перекрытий изготавливают из березовой фанеры и хвойных пород
древесины, которым свойственна повышенная влагостойкость. В процессе
изготовления балки обрабатывают специальными водонепроницаемыми составами или
водоотталкивающими красками. Благодаря такой обработке балки можно использовать
Благодаря такой обработке балки можно использовать
в строительстве при любых неблагоприятных погодных и атмосферных условиях.
Балки опалубки обладают высокой несущей способностью, и они могут с успехом
монтироваться на достаточно больших площадях (до 6 метров). При этом в процессе
эксплуатации не возникает никаких деформаций (изгибов, усадки, трещин).
Справочник строительных материалов (А)
Справочник строительных материалов и терминов
Двухпролетные балки — Доктор Лом
Рисунок 1. а) две однопролетные балки с общей опорой; б) двухпролетная балка.
Причем разница эта видна не по расчетным схемам, к которым нужно хорошо присмотреться, чтобы эту разницу увидеть (как на детской картинке-загадке «найди одно отличие»), а по эпюрам изгибающих моментов. Как видно по эпюрам «М», в обычных однопролетных шарнирных балках со смежной опорой В только нижняя часть поперечного сечения балок растягивается, а верхняя — сжимается. В шарнирной двухпролетной балке растягивающие напряжения возникают в нижней части балки в области крайних опор и в верхней части балки на средней опоре. Казалось бы, ничего сложного, все достаточно просто и наглядно, нужно просто определить значение изгибающего момента на средней опоре В, но тут нас как раз и ожидает засада. Оказывается двухпролетные балки на шарнирных опорах являются один раз статически неопределимыми и значит обычных уравнений равновесия для определения момента на опоре не достаточно.
В шарнирной двухпролетной балке растягивающие напряжения возникают в нижней части балки в области крайних опор и в верхней части балки на средней опоре. Казалось бы, ничего сложного, все достаточно просто и наглядно, нужно просто определить значение изгибающего момента на средней опоре В, но тут нас как раз и ожидает засада. Оказывается двухпролетные балки на шарнирных опорах являются один раз статически неопределимыми и значит обычных уравнений равновесия для определения момента на опоре не достаточно.
Что такое статическая неопределимость? Девушки, те которые попродвинутее, скажут, что это научное определение для давно известного выражения: «все мужики — козлы». Юноши, изучающие сопромат в паузах между окучиванием вышеупомянутых девушек, скажут, что это ужас, летящий на крыльях ночи, кошмар неоперившегося птенца, выпавшего перед сессией с последнего этажа недостроенного небоскреба. А преподаватели завалят Вас формулами и интегралами, иллюстрирующими кинематический, статический и энергетический методы расчета. И все по-своему будут правы. Ни в коей мере не собираюсь оспаривать эти точки зрения, просто попробую изложить один из методов расчета двухпролетной балки с максимальной долей наглядности.
И все по-своему будут правы. Ни в коей мере не собираюсь оспаривать эти точки зрения, просто попробую изложить один из методов расчета двухпролетной балки с максимальной долей наглядности.
Итак. Давайте разбираться, что это за момент такой на средней опоре, откуда он взялся и как влияет на расчетные параметры балки.
Если рассматривать двухпролетную балку на шарнирных опорах А, В и С как однопролетную на опорах А и С, то чтобы соблюсти принцип равновесия сил, мы должны в точке В приложить некоторую силу, другими словами сосредоточенную нагрузку, которая и будет опорной реакцией балки. Эта опорная реакция будет направлена вверх, что логично, если основная равномерно распределенная нагрузка направлена вниз. Когда мы строили эпюру моментов для однопролетной шарнирной балки при действии сосредоточенной нагрузки, то получили следующий результат:
Рисунок 149.2.1. Эпюры сил и моментов, отражающие изменение касательных и нормальных напряжений в поперечном сечении балки.
Если мы проведем пунктирные линии от максимального значения момента на промежуточной опоре В (рис. 1.б) к крайним опорам А и С, то мы получим эпюру моментов от действия опорной реакции В (на рисунке 2 обозначена бежевым цветом):
Рисунок 3. Разложение эпюры моментов для двухпролетной балки на составляющие
По сути эта эпюра, представляющая собой треугольник, ничем не отличается от показанной на рис 149.2.1, вот только сила — опорная реакция — у нас направлена в противоположную сторону, потому и эпюра расположена сверху. А еще получается что итоговая эпюра изгибающих моментов представляет собой сумму эпюр от распределенной нагрузки (рис. 1.а) и от опорной реакции В. И если это так, то значение изгибающего момента посредине пролета равно разнице этих эпюр. Осталось только выяснить, чему же именно равен момент на промежуточной опоре В.
Примечание: Понятия «положительный момент» и «отрицательный момент» очень условные. Можно считать, что момент в пролете отрицательный, как показано на рисунке 149. 2.1 и тогда момент на опоре — положительный. Это выглядит достаточно разумно, когда эпюра расположена снизу оси х. Но в технической литературе чаще встречаются противоположные обозначения: когда эпюра расположена ниже оси х — момент положительный, а когда выше оси х — отрицательный. Чтобы в дальнейшем не путаться, будем обозначать моменты так, как принято в технической литературе.
2.1 и тогда момент на опоре — положительный. Это выглядит достаточно разумно, когда эпюра расположена снизу оси х. Но в технической литературе чаще встречаются противоположные обозначения: когда эпюра расположена ниже оси х — момент положительный, а когда выше оси х — отрицательный. Чтобы в дальнейшем не путаться, будем обозначать моменты так, как принято в технической литературе.
Как мы уже говорили, определить значение момента и значения опорных реакций для двухпролетной балки, используя только обычные уравнения равновесия, не представляется возможным, но на этот случай у нас есть туз в рукаве. Ведь мы знаем, что под действием нагрузки балка прогибается (точнее центр тяжести поперечного сечения балки, расположенного на некотором расстояния от начала балки по оси х, смещается по оси у относительно оси х на некоторую величину f), при этом поперечные сечения балки далеко не всегда перпендикулярны оси х, а имеют некоторый наклон, выражаемый углом θ. А это значит, что какие бы нагрузки не действовали на рассматриваемую балку, прогиб f на опорах такой балки будет равен 0 (так как балка у нас на не подвижных опорах), а в данном случае и угол поворота поперечного сечения балки на опоре В также равен нулю. Эти знания позволяют составить нам столько дополнительных уравнений, сколько нужно. Например:
А это значит, что какие бы нагрузки не действовали на рассматриваемую балку, прогиб f на опорах такой балки будет равен 0 (так как балка у нас на не подвижных опорах), а в данном случае и угол поворота поперечного сечения балки на опоре В также равен нулю. Эти знания позволяют составить нам столько дополнительных уравнений, сколько нужно. Например:
1. Расчет двухпролетной балки с равными пролетами и симметричной нагрузкой.
1. Так как балка у нас симметричная и нагрузка на балку равномерно распределенная по всей длине, то нам достаточно рассматривать не всю балку а только левую или правую часть, как отдельную балку. Опорные реакции для такой балки будут равны
А = Влев = ql/2. (1.1.1)
при этом данное уравнение будет справедливо и для правой части балки:
С = Вправ = ql/2. (1.1.2)
а суммарная опорная реакция на опоре В для двухпролетной балки будет составлять:
В = Влев + Вправ = 2Влев = 2Вправ (1. 1.3)
1.3)
2. Чтобы такое допущение было корректным, мы должны приложить на опоре В для левой балки такой момент М, при действии которого угол поворота поперечного сечения балки на опоре В будет равен нулю, при этом на правую балку на опоре В будет действовать такой же момент М, но направленный в противоположную сторону. В этом случае суммарный момент для двухпролетной балки на опоре В будет равен нулю, и скачка на общей эпюре моментов не будет, так как моменты приложены в одной точке равны по значению и противоположны по знаку.
3. При действии изгибающего момента М как ни крути, а возникают опорные реакции. При этом опорная реакция на опоре А:
А = — М/l (1.2.1),
а опорная реакция на опоре В:
Влев = M/l (1.2.2).
4. Таким образом общая опорная реакция на опоре А будет составлять:
А = ql/2 + M/l (1. 3.1),
3.1),
а общая опорная реакция на опоре В будет составлять:
Влев = ql/2 — M/l. (1.3.2)
5. Угол поворота θ поперечного сечения балки на опоре А и на опоре В для однопролетной балки при данной нагрузке составляет:
ql3/24ЕI (174.5.6.4), (подробности определения угла поворота изложены в другой статье)
6. При действии изгибающего момента на опоре В угол поворота θ поперечного сечения балки на опоре А для однопролетной балки составляет:
Ml/6EI (1.5.1),
а на опоре В:
Ml/3EI (1.5.2)
7. Таким образом суммарный угол поворота на опоре А составит:
θА = ql3/24ЕI + Ml/6EI, (1.6.1),
а на опоре В:
θВ = ql3/24ЕI + Ml/3EI = 0 (1. 6.2)
6.2)
это уравнение (1.6.2) в данном случае и является тем самым дополнительным уравнением, позволяющим определить все накопившиеся неизвестные.
8. Из уравнения (1.6.2) мы путем простейших математических преобразований получаем значение момента на опоре В:
ql3/24ЕI = — Ml/3EI (1.6.3)
M = — ql2/8 (1.6.4)
9. Зная значение момента на опоре В, мы можем определить реакции опор по формулам (1.3) и (1.1):
А = С = ql/2 — ql/8 = 3ql/8 (1.7.1),
Влев = ql/2 + ql/8 = 5gl/8. (1.7.2)
B = 10ql/8 (1.7.3)
Зная опорные реакции и углы поворота на опорах, мы можем определить все необходимые параметры для нашей балки, хоть деревянной, хоть металлической, хоть железобетонной, но сначала не помешает сделать контрольный выстрел, например решить уравнение угла поворота:
θх = — θА + Ах2/2EI — qх3/6ЕI (174. 5.6.6)
5.6.6)
так как угол поворота поперечного сечения на опоре В равен нулю, то:
θB = — θА + Аl2/2EI — ql3/6ЕI = — ql3/24ЕI + ql3/48EI + 3ql3/16EI — ql3/6EI = 0 (1.8.2)
Все это хорошо, скажете Вы но как определить момент на опоре, если нагрузка к балке приложена не симметрично и значит угол поворота на опоре В не равен 0? Для ответа на этот вопрос мы рассмотрим
2. Расчет двухпролетной балки с равными пролетами и несимметричной нагрузкой.
Если нагрузка действует только на один пролет двухпролетной балки, при этом длины пролетов равны, то значение момента на опоре В уменьшится в 2 раза
по той простой причине, что теперь момент действует не на один пролет, как в первом примере, а на два пролета. Таким образом значение искомого момента на опоре В будет:
M = -ql2/8 х l/(l + l) = — ql2/16 (2. 1)
1)
Тогда по формулам (1.3) и (1.1):
А = ql/2 — ql/16 = 7ql/16 (2.2.1),
Влев = ql/2 + ql/16 = 9gl/16. (2.2.2)
а так как на правую часть балки нагрузка не действует, а действует только изгибающий момент, то
Bправ = ql/16 (2.2.3)
C = — ql/16 (2.2.4)
B = 9ql/16 +ql/16 = 10gl/16 (2.2.5)
И еще, из этого следует, что двухпролетную балку с равными пролетами и симметрично распределенной нагрузкой, рассмотренную в первом примере, можно рассматривать как две отдельные двухпролетные балки с равными пролетами, при этом у первой балки загружен первый пролет, а у второй балки — второй пролет. В принципе это настолько просто, что подробно и запутанно объяснить это очень сложно.
Хорошо, допустим, скажете Вы, но как быть, если пролеты у балки не равны? Для ответа на этот вопрос мы рассмотрим
3.
 Расчет двухпролетной балки с разными пролетами по длине
Расчет двухпролетной балки с разными пролетами по длине
В данном случае двухпролетную балку проще рассматривать как две отдельные двухпролетные балки. Если равномерно распределенная нагрузка приложена только к первому пролету балки, то значение момента на опоре В будет:
M1 = -ql12/8 х l1/(l1 + l2) = — ql13/(8(l1 + l2)) (3.1)
Если равномерно распределенная нагрузка приложена только ко второму пролету балки, то значение момента на опоре В будет:
M2 = -ql22/8 х l2/(l1 + l2) = — ql23/(8(l1 + l2)) (3.1)
Если равномерно распределенная нагрузка приложена к обоим пролетам балки, то значение момента на опоре В будет:
M = М1 + М2 = — q(l13 +l23)/(8(l1 + l2)) (3. 1)
1)
Из этих уравнений мы можем сделать еще несколько интересных выводов — если пролеты равны, то мы получаем уравнение (2.1) при нагрузке, действующей на один пролет, или уравнение (1.6.4) при нагрузке, действующей на оба пролета, а если длина второго пролета равна 0, то мы получаем уравнение (1.6.4) и одновременно однопролетную балку с шарнирной опорой А и жестким защемлением на опоре В. Поэтому двухпролетную балку из первого примера с равными пролетами и равномерно распределенной нагрузкой можно рассматривать как две однопролетные балки у которых одна опора шарнирная, а вторая — жесткое защемление. Такие однопролетные балки также являются один раз статически неопределимыми, на как бороться с этой статической неопределимостью, мы теперь знаем.
С определением опорных реакций для двухпролетной балки с разными пролетами больших проблем в принципе нет, однако формулы из-за различных значений пролетов получаются достаточно громоздкими.
При действии равномерно распределенной нагрузки только в первом пролете l1:
А = ql1/2 — ql13/(8l1(l1 +l2))
B = ql1/2 + ql13/(8l1(l1 +l2)) + ql13/(8l2(l1 + l2))
C = — ql13/(8l2(l1 +l2))
При действии равномерно распределенной нагрузки только во втором пролете l2:
С = ql2/2 — ql23/(8l2(l1 +l2))
B = ql2/2 + ql23/(8l1(l1 + l2)) + ql23/(8l2(l1 + l2))
А = — ql23/(8l1(l1 +l2))
Суммарные опорные реакции:
А = ql1/2 — q(l13 + l23)/(8l1(l1 + l2))
B = q(l1 + l2)/2 + q(l13 + l23)/(8l1(l1 + l2)) + q(l13 + l23)/(8l2(l1 + l2))
С = ql2/2 — q(l13 + l23)/(8l2(l1 + l2))
Не смотря на столь страшный вид, при решении конкретных задач, когда известны значения пролетов, то все выглядит не так уж страшно. Например, нужно рассчитать шарнирно опертую балку с пролетами l1 = 2.6 и l2 = 1.4 м на действие равномерно распределенной по всей длине балки нагрузки q.
Например, нужно рассчитать шарнирно опертую балку с пролетами l1 = 2.6 и l2 = 1.4 м на действие равномерно распределенной по всей длине балки нагрузки q.
Определим сначала значения общих выражений 8(l1 + l2) = 8(2.6 +1.4) = 32
и l13 + l23 = 2.63 + 1.43 = 17.576 + 2.744 = 20.32,
разделим 20.32/32 = 0.635 чтобы получить общий член для большинства уравнений
А = ql1/2 — q(l13 + l23)/(8l1(l1 + l2)) = 2.6q/2 — 0.635q/2.6 = 1.0558q
B = q(l1 + l2)/2 + q(l13 + l23)/(8l1(l1 + l2)) + q(l13 + l23)/(8l2(l1 + l2)) = 4q/2 + 0.635q/2.6 + 0.635q/1.4 = 2.6978q
С = ql2/2 — q(l13 + l23)/(8l2(l1 + l2)) = 1. 4q/2 — 0.635q/1.4 = 0.2464q
4q/2 — 0.635q/1.4 = 0.2464q
Сумма опорных реакций должна быть равно суммарной распределенной нагрузке на 4 метрах балки. Проверяем:
A + В + С = 1.0558q + 2.6978q + 0.2464q = 4q.
Позвольте, но ведь нагрузка бывает не только равномерно распределенной, скажете Вы, как быть в этом случае? А в этом случае достаточно ознакомиться с расчетными формулами для двухпролетных балок, выведенными по этому принципу, или воспользоваться уравнением трех моментов, которое подходит для любого случая загружения.
Не удается найти страницу | Autodesk Knowledge Network
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}}*
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}}
{{addToCollection.description.length}}/500
{{l10n_strings. TAGS}}
TAGS}}
{{$item}}
{{l10n_strings.PRODUCTS}}
{{l10n_strings.DRAG_TEXT}}
{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings.LANGUAGE}}
{{$select.selected.display}}
{{article.content_lang.display}}
{{l10n_strings. AUTHOR}}
AUTHOR}}
{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$select.selected.display}}
{{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}}
{{l10n_strings.CREATE_A_COLLECTION_ERROR}}
Что это за балки такие и какими разными они бывают | sevprostor
Не так давно я писала про одного отшельника, который жил в заброшенной деревне и, как мы поняли, занимался тем, что отыскивал старые балки, ремонтировал их, а потом продавал заезжим людям. Однажды у него один или несколько балков украли, и он очень по этому поводу сокрушался. Хотя, вероятно, продать кое-что тоже удалось.
Хотя, вероятно, продать кое-что тоже удалось.
Забавный коммент оставил один человек к этому рассказу:
А а что такое «балки». Варианты (выбрать):
1) сухая или с временным водотоком долина с задернованными склонами.
2) линейный элемент несущих конструкций, опирающийся на оба конца (например, горизонтальный брус, служащий связью между стенами).
3) размытая водой поверхность земли в виде ложбины.
Я бы выбрал любой, для того, чтобы «ремонтировать», но смущает следующая фраза : «Однажды у него один или несколько балков украли, и он очень по этому поводу сокрушался». Внушает сомнение правильность склонения слова » балка».
Поэтому и непонятно, что она из себя представляет, раз её так склоняют…:)
Там же ему пояснили, что балок это вот такой «вагончик» как на фото. Часто он стоит на специальных полозьях и таким образом балки можно таскать трактором куда угодно по тундре. Поэтому это очень популярный вид сезонного жилья на севере.
Часто он стоит на специальных полозьях и таким образом балки можно таскать трактором куда угодно по тундре. Поэтому это очень популярный вид сезонного жилья на севере.
А вообще балки бывают очень разной конструкции. Например, они могут быть вот такими:
Это цельнометаллические универсальные блоки (ЦУБы), в них жили люди, участвующие в строительстве БАМа, и военные, и геологи, и многие другие специалисты, которым нужно мобильное жилье где-нибудь в тундре.
Чей-то рисунок, автора не знаю
Чей-то рисунок, автора не знаю
Сейчас, разумеется, на всевозможных объектах используются совсем другие жилые модули, а в старых ЦУБах часто живут охотники и рыбаки. Ну и рабочие на предприятиях победнее — тоже, потому как несмотря на возраст, это довольно удобное жилье. Вот такой же ЦУБ стоит на Лесозаводе в Нарьян-Маре.
А вот такой балок стоял на Медынке, в советские времена здесь располагалось что-то вроде склада обеспечения различных экспедиций. Тут хранились балки, нефтяное оборудование…
Тут хранились балки, нефтяное оборудование…
Также балки могут быть, например, и такими.
Это не какой-нибудь типовой кунг от машины и не современное изделие, а явно что-то довольно старое. Сейчас таких вагончиков никто не делает.
Пример балка, сделанного из кунга
Пример балка, сделанного из кунга
Похожие балки мы видали и в другом месте на Вайгаче. Правда, там они были крупнее, но имели очень похожую конструкцию: полукруглые своды крыши, все полностью сделано из дерева. Речь идет о так называемых «медных балках» в районе губы Долгой, и там эти постройки можно датировать примерно пятидесятыми годами прошлого века.
Под словом «крупнее» я имею в виду то, что там эти домики имели размеры самых настоящих домов. Я полагаю, что по фотографии это отлично заметно: на короткой стенке умещается целых два окна, а внутри там были полноценные комнаты. Удивительно, что такое изделие тоже было мобильным и перемещалось при помощи трактора.
Полоз станины балка. Просто, чтобы вы понимали масштаб.
Полоз станины балка. Просто, чтобы вы понимали масштаб.
Но чаще всего сейчас балками служат вот такие небольшие фургончики:
А в последнее время, в связи с очередной волной освоения Севера, кое-где можно встретить и вовсе очень интересные самодельные конструкции. Вот, например, «дом» какой-то охотничьей базы. Он построен из нескольких морских контейнеров, соединенных болтами, и в разборе все элементы сооружения, как водится, перемещались по земле при помощи тракторов. На месте же они составлялись как задумано, и собирались в один цельный комплекс.
Металлические балки
Вернуться в раздел «Металлические конструкции»
Стальные балки
Балка – это элемент строительной конструкции, работающий на изгиб. Применяются балки для перекрытия пролетов промышленных и гражданских зданий. Рационально использовать балки для перекрытия пролетов не более 8-12 метров, т. к. дальнейшее использование балок экономически не целесообразно и следует использовать фермы и другие стержневые конструкции.
к. дальнейшее использование балок экономически не целесообразно и следует использовать фермы и другие стержневые конструкции.
РАСЧЕТЫ
Балки считают как изгибаемые элементы.
Расчет изгибаемых элементов
Расчет балок на момент и прогиб
ЧЕРТЕЖИ
Начинаем чертить со схемы расположения балок. Это может быть раздел КМ, КМД или АС.
СМОТРЕТЬ ЧЕРТЕЖ: СХЕМА РАСПОЛОЖЕНИЯ БАЛОК
Чертежи балок мы будем рассматривать совместно с опорным узлом балки. Второстепенные балки опираются, как правило, на главные балки. Главные балки опираются на колонны. Опорные узлы могут быть шарнирные и жесткие.
СМОТРЕТЬ ЧЕРТЕЖИ: ПРИМЫКАНИЕ ВТОРОСТЕПЕННОЙ БАЛКИ К ГЛАВНОЙ БАЛКЕ.
СМОТРЕТЬ ЧЕРТЕЖИ: ШАРНИРНЫХ УЗЛОВ ПРИМЫКАНИЯ БАЛОК К КОЛОННЕ.
СМОТРЕТЬ ЧЕРТЕЖИ: ЖЕСТКИХ УЗЛОВ ПРИМЫКАНИЯ БАЛОК К КОЛОННЕ.
СМОТРЕТЬ ЧЕРТЕЖИ: БАЛОК
ОБЩАЯ ИНФОРМАЦИЯ
Типы балок по статической схеме.
Разрезные балки – это балки, которые опираются на двух шарнирных опорах и перекрывает один пролет. Разрезные балки наиболее металлоемкие, но отличаются простотой монтажа и нечувствительностью к неравномерной осадке опор.
Разрезные балки наиболее металлоемкие, но отличаются простотой монтажа и нечувствительностью к неравномерной осадке опор.
Неразрезные балки – это балки, которые опираются на нескольких опорах и перекрывают несколько пролетов. Неразрезные балки менее металлоемкие по сравнению с разрезными балками, но более сложные при монтаже и чувствительны к неравномерной осадке опор.
Консольные балки – это балки, которые имеют консольный участок.
Типы балок по форме сечения.
Цельные балки – это балки, выполненные из одного профиля. Как правило, используются балки двутаврового сечения.
Сварные балки – это балки, сваренные из стальных листов. Используются при больших нагрузках, когда несущей способности цельных балок недостаточно.
Составные балки – это балки, выполненные из стальных листов с поясными уголками и т.п.
Специальные балки.
В целях уменьшения металлоемкости балок больших пролетов, разработаны специальные типы балок. Металлоемкость этих балок снижается за счет металлоемкости стенки балок. К таким балкам относятся перфорированные балки и гофрированные балки.
Металлоемкость этих балок снижается за счет металлоемкости стенки балок. К таким балкам относятся перфорированные балки и гофрированные балки.
Перфорированные балки – это балки, полученные в результате продольного разрезания двутаврового горячекатаного профиля ломаной линией с последующим сдвигом до стыка гребней и сваркой. За счет этого достигается значительное увеличение несущей способности балки. Снижение металлоемкости достигает 20-30%.
Гофрированные балки – это балки, полученные путем сварки поясов произвольного сечения и тонкой гофрированной стенкой.
При проектировании прогонов и балок могут быть полезны следующие типовые серии:
| № п/п | Номер | Наименование | Примечания |
| 1 | Серия 1.462.3-17/85 | Стальные решетчатые прогоны производственных зданий пролетом 12 м с применением профилей по сокращенному сортаменту металлопроката. Чертежи КМ. | Смотреть |
| 2 | Серия 1. 462.3-22 462.3-22 | Прогоны стальные производственных зданий. | Смотреть |
ИТ-решения
Beams | Компания-разработчик программного обеспечения Дубай
Beams IT Solutions | Компания-разработчик программного обеспечения в Дубае — Crunchbase Профиль компании и финансирование
Beams IT Solutions — компания по разработке программного обеспечения, базирующаяся в Дубае, занимающаяся консалтингом в области программного обеспечения, разработкой, аутсорсингом и веб-решениями.
- Промышленность
- Отрасли
- Штаб-квартиры Совет по сотрудничеству залив (GCC)
- Основан дата 1, 2004 г.
- Операционный статус Active
- , также известный как лучи ERP, биты Soft
- Юридическое название Beams IT Solutions
- Контактное письмо продажи@beamserp.
 com
com - Номер телефона 971551934752
Beams является одним из пионеров программного обеспечения ERP. Основанная в 2007 году в Дубае Мухаммедом Шахимом с четким видением: путем предоставления доступных, гибких и простых в использовании решений стать одним из ведущих партнеров по услугам управления бизнесом в странах Персидского залива. Усилиями команды дальновидных инженеров-программистов и консультантов мы разработали Beams
ERP — специально разработанное индивидуальное ERP-решение для всех предприятий.
Слово «Beams» в нашем названии отражает наши стратегии направления, луч оптимизирует ваши бизнес-задачи с помощью нашего гибкого программного обеспечения для управления.За последние 14 лет Professional Advantage выросла до команды из 25 сотрудников в двух офисах. За последние 10 лет мы работали с более чем 1000 клиентов и реализовали более 500 проектов. В 2019 году Beams расширила свои услуги и в Индии. Мы органично выросли и расширились по всему миру.
 Никаких инвесторов, только наш собственный успех. Мы олицетворяем классический успех на среднем рынке благодаря творчеству нашей целеустремленной команды.
Никаких инвесторов, только наш собственный успех. Мы олицетворяем классический успех на среднем рынке благодаря творчеству нашей целеустремленной команды.Подробнее
Выберите подходящее решение Crunchbase
Условия обслуживания | Политика конфиденциальности | Карта сайта | © 2022 Кранчбейс Инк.Все права защищены. (0.1.12699 596)
Расположение штаб-квартиры
Количество сотрудников
Статус IPO
Веб-сайт
CB Rank (Company)
Общее количество профилей сотрудников организации на Crunchbase
, Android, облачные вычисления, медицинское устройство)
Местонахождение штаб-квартиры организации (например, область залива Сан-Франциско, Силиконовая долина)
Дата основания организации
Операционный статус организации e.г. Активная, закрытая
Альтернативное или прежнее название организации
Официальное название организации
Является ли организация коммерческой или некоммерческой
Общий контактный адрес электронной почты для организации
Общий номер телефона организации
Перемещение лучей при нормальном падении посредством управления геометрическими фазами импульс-пространство
Основной принцип
Для параксиального светового луча поведение его распространения в свободном пространстве может быть описано его пространственным положением и направлением распространения.
 {2}}\).
{2}}\).Учитывая определение оператора координат в плоскости \(\hat{{{{{{{{\bf{r}}}}}}}}}}\) и оператора импульса \(\hat{{{{ {{{{\bf{p}}}}}}}}}\) и их ожидаемые значения, которые подробно описаны в дополнительном примечании 1, мы можем получить выражения 〈 R 〉 и 〈 P 〉 с приведенные выше выражения поля,
$$\langle {{{{{{{\bf{P}}}}}}}}\rangle =\left\langle \frac{\partial \varphi ({{{{{ {{{\boldsymbol{r}}}}}}}}}}_{\parallel})}{\partial {{{{{{{{\boldsymbol{r}}}}}}}}}}_{\ параллельно }}\right\rangle ,\\ \langle {{{{{{{\bf{R}}}}}}}}}\rangle =-\left\langle \frac{\partial (\phi ({{ {{{{{{\boldsymbol{k}}}}}}}}}_{\parallel})+{k}_{{{{{{\rm{z}}}}}}}}({{ {{{{{{\boldsymbol{k}}}}}}}}}}_{\parallel})z)}{\partial {{{{{{{{\boldsymbol{k}}}}}}}} }}_{\parallel}}\right\rangle \\ = {{{{{{{{\bf{R}}}}}}}}}}_{{{{{{{{{\rm{c}} }}}}}}}}}-\left\langle \frac{\partial \phi ({{{{{{{{\boldsymbol{k}}}}}}}}}}_{\parallel})}{ \partial {{{{{{{{\boldsymbol{k}}}}}}}}}}_{\parallel}}\right\rang ле,$$
(2)
где R c — независимая от ϕ константа.
 Как пара обратных пространств, световые поля реального пространства и импульсного пространства тесно коррелированы. Следовательно, \( < {{{{{{{\bf{R}}}}}}}} > \) и \( < {{{{{{{\bf{P}}}}}}}}} > 1) можно модулировать фазовыми распределениями в соответствующем обратном пространстве. Модуляции φ в реальном пространстве вызовут изменения на \( < {{{{{{\bf{P}}}}}}}}} > \), изменяя направление распространения. Исходя из этого принципа, аномальное отражение и преломление световых лучей метаповерхностями можно понимать как эффекты модулированных фазовых градиентов реального пространства 31 .Точно так же, если мы можем модулировать распределение фазы импульсного пространства ϕ , модуляция на \( < {{{{{{\bf{R}}}}}}}} > \) светового луча могут быть реализованы, т. е. световые лучи могут быть смещены в реальном пространстве. Как схематично показано на рис. 1а, если градиент фазы ввести в серию плоских волн, составляющих луч, результирующий новый луч будет смещаться в соответствии с градиентом фазы в направлении уменьшения дополнительной фазы.
Как пара обратных пространств, световые поля реального пространства и импульсного пространства тесно коррелированы. Следовательно, \( < {{{{{{{\bf{R}}}}}}}} > \) и \( < {{{{{{{\bf{P}}}}}}}}} > 1) можно модулировать фазовыми распределениями в соответствующем обратном пространстве. Модуляции φ в реальном пространстве вызовут изменения на \( < {{{{{{\bf{P}}}}}}}}} > \), изменяя направление распространения. Исходя из этого принципа, аномальное отражение и преломление световых лучей метаповерхностями можно понимать как эффекты модулированных фазовых градиентов реального пространства 31 .Точно так же, если мы можем модулировать распределение фазы импульсного пространства ϕ , модуляция на \( < {{{{{{\bf{R}}}}}}}} > \) светового луча могут быть реализованы, т. е. световые лучи могут быть смещены в реальном пространстве. Как схематично показано на рис. 1а, если градиент фазы ввести в серию плоских волн, составляющих луч, результирующий новый луч будет смещаться в соответствии с градиентом фазы в направлении уменьшения дополнительной фазы. Учитывая механизм, можно разместить пространственные модуляторы света в плоскостях Фурье классических оптических путей для искусственного смещения лучей.Обычные сдвиги светового луча, такие как хорошо известные сдвиги G-H и I-F, могут быть приписаны фазовым градиентам импульс-пространство, вызванным процессами отражения или преломления на границах раздела.
Учитывая механизм, можно разместить пространственные модуляторы света в плоскостях Фурье классических оптических путей для искусственного смещения лучей.Обычные сдвиги светового луча, такие как хорошо известные сдвиги G-H и I-F, могут быть приписаны фазовым градиентам импульс-пространство, вызванным процессами отражения или преломления на границах раздела.Рис. 1. Концепция реализации поляризационно-зависимых латеральных смещений нормально падающих гауссовских лучей с помощью пластин фотонного кристалла (PhC).
a Схематическое изображение сдвига луча, вызванного фазовым градиентом в импульсном пространстве. Луч можно рассматривать как суперпозицию плоских волн.При введении дополнительного фазового градиента к плоским волнам в импульсном пространстве луч будет смещаться в реальном пространстве в направлении, противоположном градиенту. b Иллюстрации прикладной конструкции пластины ФК, не имеющей инверсионной симметрии в плоскости (верхняя панель), соответствующей структуры собственных состояний поляризации вблизи центра импульсного пространства (средняя панель) и геометрического фазового распределения, введенного формулой плита PhC вдоль направления k x с \(\left|-45\right\rangle\)-поляризованным падающим лучом (нижняя панель).
 c Схематическое изображение бокового смещения, реализованного разработанной плитой PhC. \(\left|-45\right\rangle\) поляризованный луч светит нормально, и после процесса рассеяния рассеянное поле можно рассматривать как четыре рассеянных луча: прямо передающий и отражающий лучи и кросс-поляризационно преобразованный передающие и отражающие лучи. Преобразованные кросс-поляризацией лучи будут смещены в направлении, противоположном фазовому градиенту импульс-пространство.
c Схематическое изображение бокового смещения, реализованного разработанной плитой PhC. \(\left|-45\right\rangle\) поляризованный луч светит нормально, и после процесса рассеяния рассеянное поле можно рассматривать как четыре рассеянных луча: прямо передающий и отражающий лучи и кросс-поляризационно преобразованный передающие и отражающие лучи. Преобразованные кросс-поляризацией лучи будут смещены в направлении, противоположном фазовому градиенту импульс-пространство.Среди обычных сдвигов луча сдвиги I–F представляют собой зависящие от поляризации поперечные сдвиги, которые, как известно, являются результатом геометрических фазовых градиентов 8,9,10,11 .Лучи с двумя определенными ортогональными поляризациями будут иметь противоположные фазовые градиенты, что приведет к противоположным направлениям смещения. Ограниченные свойствами материала интерфейса, сдвиги IF чрезвычайно малы. Один из способов увеличить и контролировать сдвиги луча, зависящие от поляризации, — создать геометрические фазовые градиенты в импульсном пространстве путем реализации нанофотонных структур.
 Плиты PhC, которые имеют определяемые режимы излучения, состоящие из состояний фотонных полос 32,33,34,35,36 , являются идеальными платформами для выполнения модуляции света в импульсном пространстве 37,38,39,40 .Для пластины PhC ее излучательные резонансные моды с различными волновыми векторами в плоскости внутри светового конуса могут взаимодействовать с плоскими волнами в свободном пространстве из-за взаимности. Хотя моды имеют разные длины собственных волн, их утечка приводит к конечному времени жизни и, следовательно, к конечной ширине пика как длины волны, так и плоского волнового вектора. В результате монохроматический пучок конечного размера, состоящий из серии плоских волн, может возбудить резонансные моды, которые охватывают область в импульсном пространстве, даже если существует несоответствие длин волн.Благодаря связи компоненты падающего луча с определенными состояниями поляризации будут частично преобразованы в компоненты с ортогональными состояниями поляризации.
Плиты PhC, которые имеют определяемые режимы излучения, состоящие из состояний фотонных полос 32,33,34,35,36 , являются идеальными платформами для выполнения модуляции света в импульсном пространстве 37,38,39,40 .Для пластины PhC ее излучательные резонансные моды с различными волновыми векторами в плоскости внутри светового конуса могут взаимодействовать с плоскими волнами в свободном пространстве из-за взаимности. Хотя моды имеют разные длины собственных волн, их утечка приводит к конечному времени жизни и, следовательно, к конечной ширине пика как длины волны, так и плоского волнового вектора. В результате монохроматический пучок конечного размера, состоящий из серии плоских волн, может возбудить резонансные моды, которые охватывают область в импульсном пространстве, даже если существует несоответствие длин волн.Благодаря связи компоненты падающего луча с определенными состояниями поляризации будут частично преобразованы в компоненты с ортогональными состояниями поляризации. Геометрические фазовые изменения, зависящие от волнового вектора (фаза Панчаратнама-Берри или P-B 41,42 ), будут индуцироваться в кросс-поляризованных исходящих компонентах процессом преобразования в дополнение к фазовым изменениям, вызванным резонансом. Если дополнительно зафиксировать состояние поляризации падающего луча и анализируемое состояние поляризации выходящего луча как ортогональные, относительные значения фазовых изменений P–B будут определяться промежуточными собственными состояниями поляризации взаимодействующих резонансов.Можно видеть, что распределение собственных состояний поляризации в импульсном пространстве вводит соответствующее геометрическое фазовое распределение в луч с определенным процессом поляризации-анализа 38,39,40 . Управляя состояниями поляризации падающего и анализируемого луча и выбирая хорошо структурированную пластину PhC, мы можем спроектировать фазовое распределение анализируемого луча в импульсном пространстве и его градиент.
Геометрические фазовые изменения, зависящие от волнового вектора (фаза Панчаратнама-Берри или P-B 41,42 ), будут индуцироваться в кросс-поляризованных исходящих компонентах процессом преобразования в дополнение к фазовым изменениям, вызванным резонансом. Если дополнительно зафиксировать состояние поляризации падающего луча и анализируемое состояние поляризации выходящего луча как ортогональные, относительные значения фазовых изменений P–B будут определяться промежуточными собственными состояниями поляризации взаимодействующих резонансов.Можно видеть, что распределение собственных состояний поляризации в импульсном пространстве вводит соответствующее геометрическое фазовое распределение в луч с определенным процессом поляризации-анализа 38,39,40 . Управляя состояниями поляризации падающего и анализируемого луча и выбирая хорошо структурированную пластину PhC, мы можем спроектировать фазовое распределение анализируемого луча в импульсном пространстве и его градиент.
Здесь мы показываем одну конкретную конструкцию пластины PhC для выполнения пространственно-импульсной фазовой инженерии и реализации больших боковых сдвигов нормально падающих гауссовых пучков.Это отдельно стоящая пластина из нитрида кремния (Si 3 N 4 ) PhC с квадратной решеткой из равнобедренно-треугольных отверстий, как показано на верхней панели рис. 1b. Симметрия разработана таким образом, что симметрия инверсии в плоскости нарушается и сохраняется только одна ось зеркала в плоскости. Соответственно, излучательные резонансные моды вблизи центра ее зоны Бриллюэна будут иметь зеркально-симметричную поляризационную структуру, в которой будет происходить переход от состояния с левой круговой поляризацией (LCP) к состоянию с правой круговой поляризацией (RCP) вдоль направление, перпендикулярное оси зеркала, как схематично показано на средней панели рис.1б.
Воспользовавшись разработанной структурой поляризации, которую мы показали, мы здесь выбираем два состояния линейной поляризации, нормированные вторые параметры Стокса S 2 /S 0 равны ±1, а не обычно выбираемую круговую поляризацию состояний, чтобы быть фиксированной падающей и анализирующей поляризацией.
 Мы помечаем эти два линейных состояния поляризации как ‘кет \(\лево|+45\право\угол\) и \(\лево|-45\право\угол\), а соответствующие анализируемые состояния поляризации — это ‘бюстгалтеры \( \left\langle +45\right|\) и \(\left\langle -45\right|\) для упрощения обозначений.{i {{\Delta}}{\phi}_{\left|\pm 45\right\rangle}}, \\ {{\Delta}}{\phi} _{\left|\pm 45\right\ rangle } =\mp \left[\arg ({{{{{S}}}}}_{3}+i{{{{{S}}}}}_{1})-\frac{\pi {2}\справа].$$
Мы помечаем эти два линейных состояния поляризации как ‘кет \(\лево|+45\право\угол\) и \(\лево|-45\право\угол\), а соответствующие анализируемые состояния поляризации — это ‘бюстгалтеры \( \left\langle +45\right|\) и \(\left\langle -45\right|\) для упрощения обозначений.{i {{\Delta}}{\phi}_{\left|\pm 45\right\rangle}}, \\ {{\Delta}}{\phi} _{\left|\pm 45\right\ rangle } =\mp \left[\arg ({{{{{S}}}}}_{3}+i{{{{{S}}}}}_{1})-\frac{\pi {2}\справа].$$(3)
Здесь S 0 , S 1 , S 3 — нулевой, первый и третий параметры Стокса состояния поляризации резонансной моды, которые равны 9 k9000, 3 ∥ -зависимый. t a,b — константы, не зависящие от инцидентности, содержащие резонансный эффект. Ясно, что разности наведенной геометрической фазы \({{\Delta}}{\phi}_{\left|\pm 45\right\rangle }\) плоской волны с удельным k ∥ зависят только от двух параметров Стокса S 1 и S 3 собственных состояний поляризации резонансной моды PhC, которые варьируются в импульсном пространстве.
 Приведенное выше уравнение показывает, что профиль поля поляризации на рис.1б показано фазовое распределение P–B, в котором результирующий фазовый градиент {\parallel})}{\partial {{{{{{{{\boldsymbol{k}}}}}}}}}}_{\parallel}}\right\rangle\) в k x направление может быть получено, как показано на нижней панели рис. 1b. Как объясняется уравнением (2), этот искусственный фазовый градиент может вызвать сдвиг анализируемого луча в реальном пространстве. Например, нормально падающий \(\влево|\pm 45\вправо\угол\) луч будет иметь отрицательное (положительное) x -направленное смещение после соединения с спроектированной плитой и анализа с помощью \(\влево\ langle \mp 45\right|\) поляризатор, как показано на рис.1с.
Приведенное выше уравнение показывает, что профиль поля поляризации на рис.1б показано фазовое распределение P–B, в котором результирующий фазовый градиент {\parallel})}{\partial {{{{{{{{\boldsymbol{k}}}}}}}}}}_{\parallel}}\right\rangle\) в k x направление может быть получено, как показано на нижней панели рис. 1b. Как объясняется уравнением (2), этот искусственный фазовый градиент может вызвать сдвиг анализируемого луча в реальном пространстве. Например, нормально падающий \(\влево|\pm 45\вправо\угол\) луч будет иметь отрицательное (положительное) x -направленное смещение после соединения с спроектированной плитой и анализа с помощью \(\влево\ langle \mp 45\right|\) поляризатор, как показано на рис.1с.Следует отметить, что сдвиг может произойти даже без выбора определенной поляризации выхода. В этом случае смещение будет уменьшено, поскольку переданный луч представляет собой смесь как сдвинутого кросс-поляризованного луча, так и несмещенного луча с совместной поляризацией без геометрического фазового градиента импульс-пространство.

Результаты моделирования и обсуждение
Чтобы экспериментально продемонстрировать описанный выше подход к реализации боковых сдвигов, мы масштабировали нашу конструкцию отдельно стоящей плиты PhC для работы в ближнем инфракрасном спектре.Толщина t пластины выбрана равной 100 нм, а период протравленного массива a = 660 нм. Высота h и длина базовой линии w вытравленных равнобедренных треугольников равны ( h = w = 550 нм). Все параметры здесь выбираются свободно, только с учетом простоты изготовления, и изменения не повлияют на возникновение сдвигов луча. На рис. 2а показана рассчитанная ТЕ-подобная полоса структуры вдоль направлений Γ-X и Γ-X′ ( k y = 0 и k x = 0 соответственно), где «TE» означает поперечный электрический.Собственные состояния поляризации в дальнем поле излучательных мод на второй ТЕ-подобной полосе (TE 2 ) показаны в виде эллипсов поляризации на рис.
 2b. Красные (синие) эллипсы соответствуют правосторонним (левосторонним) состояниям поляризации, а точки с круговой поляризацией мы отметили соответственно соответствующими цветными точками. Видно, что структура поляризации и нормированные третьи параметры Стокса ( S 3 / S 0 ) зеркально антисимметричны, а большие оси эллипсов поляризации в основном горизонтальны.Другими словами, нормированный третий параметр Стокса собственных состояний поляризации изменится с отрицательного на положительный в направлении k x , проходящем через линейно поляризованную линию ( S 3 / S 0 ≥== ), а нормализованный второй параметр Стокса ( S 2 / S 0 ) держится около нуля, как мы и ожидали. Это распределение поляризации — то, что нам нужно, чтобы вызвать градиенты геометрической фазы в импульсном пространстве для луча.
2b. Красные (синие) эллипсы соответствуют правосторонним (левосторонним) состояниям поляризации, а точки с круговой поляризацией мы отметили соответственно соответствующими цветными точками. Видно, что структура поляризации и нормированные третьи параметры Стокса ( S 3 / S 0 ) зеркально антисимметричны, а большие оси эллипсов поляризации в основном горизонтальны.Другими словами, нормированный третий параметр Стокса собственных состояний поляризации изменится с отрицательного на положительный в направлении k x , проходящем через линейно поляризованную линию ( S 3 / S 0 ≥== ), а нормализованный второй параметр Стокса ( S 2 / S 0 ) держится около нуля, как мы и ожидали. Это распределение поляризации — то, что нам нужно, чтобы вызвать градиенты геометрической фазы в импульсном пространстве для луча.Рис.
 2: Результаты моделирования пластины PhC, примененной для реализации зависимых от поляризации боковых смещений.
2: Результаты моделирования пластины PhC, примененной для реализации зависимых от поляризации боковых смещений. a Имитация поперечной электрической (TE-подобной) зонной структуры вдоль направлений Γ-X и Γ-X’. Полоса, на которую мы обращаем внимание, — это вторая ТЕ-подобная полоса (TE 2 ), отмеченная сплошной линией. Мы применяем эту полосу для реализации бокового смещения нормально падающего гауссова луча, в котором мы принимаем 820 нм в качестве рабочей длины волны, отмеченной оранжевой пунктирной линией. b Смоделированная структура собственных состояний поляризации полосы TE 2 в окрестности точки Γ.Красный (синий) цвет соответствует правосторонним (левосторонним) собственным состояниям поляризации. Красные (синие) точки соответствуют правосторонней (левосторонней) круговой поляризованной точке. c Смоделированная кросс-поляризованная эффективность преобразования, зависящая от волнового вектора, между состояниями поляризации \(\left|\pm 45\right\rangle\) для проходящего света на длине волны 820 нм.
 d Моделированное фазовое распределение, зависящее от волнового вектора, вызванное преобразованием \(\left|\pm 45\right\rangle\) в \(\left|\mp 45\right\rangle\) на длине волны 820 нм.Верхний график: \(\left|+45\right\rangle\) падение и \(\left\langle -45\right|\) анализ; нижний график: \(\left|-45\right\rangle\) падение и \(\left\langle +45\right|\) анализ. e Вид сверху ( z = -1,5 мкм) и поперечное сечение ( y = 0 мкм) реализованных латеральных сдвигов на 820 нм путем моделирования. Нормально падающий гауссовский луч имеет центр в точке ( x = 0, y = 0). Показаны только исходящие лучи с преобразованными состояниями поляризации путем применения анализирующих матриц Джонса \(\left\langle \mp 45\right|\) к смоделированным полям.Цветовая карта нормализована в соответствии с максимальной интенсивностью луча, делая насыщенным цвет поля внутри плиты, усиленный направленными резонансами. Для ясности мы отмечаем положения максимумов смещенных лучей вместо центроидов.
d Моделированное фазовое распределение, зависящее от волнового вектора, вызванное преобразованием \(\left|\pm 45\right\rangle\) в \(\left|\mp 45\right\rangle\) на длине волны 820 нм.Верхний график: \(\left|+45\right\rangle\) падение и \(\left\langle -45\right|\) анализ; нижний график: \(\left|-45\right\rangle\) падение и \(\left\langle +45\right|\) анализ. e Вид сверху ( z = -1,5 мкм) и поперечное сечение ( y = 0 мкм) реализованных латеральных сдвигов на 820 нм путем моделирования. Нормально падающий гауссовский луч имеет центр в точке ( x = 0, y = 0). Показаны только исходящие лучи с преобразованными состояниями поляризации путем применения анализирующих матриц Джонса \(\left\langle \mp 45\right|\) к смоделированным полям.Цветовая карта нормализована в соответствии с максимальной интенсивностью луча, делая насыщенным цвет поля внутри плиты, усиленный направленными резонансами. Для ясности мы отмечаем положения максимумов смещенных лучей вместо центроидов. Порядок графиков такой же, как у d .
Порядок графиков такой же, как у d .Как показано на рис. 2c, мы получили k ∥ -зависимую карту кросс-поляризованной эффективности преобразования между двумя состояниями ортогональной линейной поляризации (\(\left|+45\right\rangle\) и \(\left|-45\right\rangle\)) на длине волны 820 нм, которая определяет угол расходимости, который мы бы взяли для падающего луча.Затем рассчитываются разности фаз в импульсном пространстве, вызванные PhC-пластиной, как показано на рис. 2d. Можно обнаружить, что для каждого случая, когда поляризация \(\left|\pm 45\right\rangle\) преобразуется в \(\left|\mp 45\right\rangle\), индуцированная геометрическая фаза имеет тенденцию к уменьшается в сторону увеличения S 3 / S 0 , что согласуется с уравнением (3). Кроме того, фазовое распределение в импульсном пространстве зависит от поляризации: когда мы поменяем поляризатор и анализатор, фазовое распределение будет зеркально отражено.
 Принимая во внимание введенный нами основной принцип, можно реализовать зависящие от поляризации боковые сдвиги луча. Отметим, что на каждой из рассчитанных фазовых карт можно наблюдать фазовое искажение. Эти фазовые искажения вызваны динамическими фазовыми сдвигами, индуцированными резонансами, которые зеркально симметричны оси k y . Сдвиг луча нормально падающих лучей в направлении x должен быть результатом только геометрического фазового распределения из-за зеркальной симметрии.Подробное обсуждение резонансных фаз см. в дополнительном примечании 2 и примечании 5.
Принимая во внимание введенный нами основной принцип, можно реализовать зависящие от поляризации боковые сдвиги луча. Отметим, что на каждой из рассчитанных фазовых карт можно наблюдать фазовое искажение. Эти фазовые искажения вызваны динамическими фазовыми сдвигами, индуцированными резонансами, которые зеркально симметричны оси k y . Сдвиг луча нормально падающих лучей в направлении x должен быть результатом только геометрического фазового распределения из-за зеркальной симметрии.Подробное обсуждение резонансных фаз см. в дополнительном примечании 2 и примечании 5.Боковые сдвиги нормального свечения, реализованные пластиной PhC, затем подтверждаются моделированием на образце конечного размера, состоящем из 120 × 120 элементарных ячеек. Гауссовский пучок 820 нм обычно освещается в центре ( x = y = 0) образца. Угол расходимости луча выбран равным примерно 2,5 градусам, покрывая область с высокой эффективностью преобразования в импульсном пространстве, как показано на рис.
 2в. Здесь, на рис. 2e, мы наносим изображения сверху в плоскости x — y вместе с видами поперечного сечения x = 0 смоделированных световых полей. Обратите внимание, что поля уже проанализированы кросс-поляризацией, так что можно увидеть только исходящий пучок, преобразованный резонансами, чтобы увидеть сдвиги луча, а поля без анализа включены в Дополнительное примечание 6 для сравнения. Около 43 % падающей мощности напрямую проходит через пластину, 23 % падающей мощности прямо отражается, 3 % теряется из-за конечного размера образца и около 15 % (15 %) падающей мощности преобразуется. в прошедший (отраженный) кросс-поляризованный пучок.Можно непосредственно наблюдать, что преобразованный пучок смещается влево ( x пик ~-4,6 микрона) в случае \(\left|+45\right\rangle\)-поляризованного падающего луча, и к правый ( x пик ~ 4,6 мкм) в другом случае (\(\left|-45\right\rangle\)-поляризованный). Результаты хорошо согласуются с нашим теоретическим предсказанием о том, что луч будет смещаться в сторону уменьшения фазы, которая контролируется поляризацией луча.
2в. Здесь, на рис. 2e, мы наносим изображения сверху в плоскости x — y вместе с видами поперечного сечения x = 0 смоделированных световых полей. Обратите внимание, что поля уже проанализированы кросс-поляризацией, так что можно увидеть только исходящий пучок, преобразованный резонансами, чтобы увидеть сдвиги луча, а поля без анализа включены в Дополнительное примечание 6 для сравнения. Около 43 % падающей мощности напрямую проходит через пластину, 23 % падающей мощности прямо отражается, 3 % теряется из-за конечного размера образца и около 15 % (15 %) падающей мощности преобразуется. в прошедший (отраженный) кросс-поляризованный пучок.Можно непосредственно наблюдать, что преобразованный пучок смещается влево ( x пик ~-4,6 микрона) в случае \(\left|+45\right\rangle\)-поляризованного падающего луча, и к правый ( x пик ~ 4,6 мкм) в другом случае (\(\left|-45\right\rangle\)-поляризованный). Результаты хорошо согласуются с нашим теоретическим предсказанием о том, что луч будет смещаться в сторону уменьшения фазы, которая контролируется поляризацией луча. Рассчитанный сдвиг луча для каждого случая примерно в 6 раз превышает длину волны и близок к радиусу перетяжки луча (~ 6 микрон).Будучи достаточно большими, смещения пучка хорошо видны и поэтому желательны для применения.
Рассчитанный сдвиг луча для каждого случая примерно в 6 раз превышает длину волны и близок к радиусу перетяжки луча (~ 6 микрон).Будучи достаточно большими, смещения пучка хорошо видны и поэтому желательны для применения.Кроме того, применяемая поляризационная структура настраивается путем изменения геометрии отверстий 33 , что позволяет нам настраивать сдвиги луча. Изменяя параметр нарушения симметрии инверсии дырок, мы можем изменять фазовый градиент импульсного пространства и, следовательно, сдвиг луча непрерывно. Чтобы доказать перестраиваемость, мы провели моделирование, в котором наблюдались сдвиги луча с различными смещениями.Тщательно настроив структуру поляризации, теоретически смещение может даже превысить радиус перетяжки. Обсуждения можно найти в дополнительном примечании 3, примечании 4, примечании 7 и примечании 11, в которых мы также проверили соответствие между прогнозируемыми размерами смещений центроида луча и смоделированными. Важно отметить, что мы показываем только один конкретный дизайн в соответствии с нашим принципом проектирования.
 Все плоские структуры с той же симметрией, что и показанная, на самом деле имеют аналогичные структуры поляризации в импульсном пространстве 33,34,35,36 , и, таким образом, все они могут быть применены для реализации подобных сдвигов луча.
Все плоские структуры с той же симметрией, что и показанная, на самом деле имеют аналогичные структуры поляризации в импульсном пространстве 33,34,35,36 , и, таким образом, все они могут быть применены для реализации подобных сдвигов луча.Экспериментальные результаты и обсуждение
Мы изготовили разработанную плиту ФК путем травления отверстий в окне Si 3 N 4 на кремниевой опорной раме с помощью электронно-лучевой литографии и метода реактивно-ионного травления (см. раздел «Методы» для получения подробной информации). Толщина оконной пленки составляет около 100 нм, а общее количество элементарных ячеек составляет 146 × 146. Мы применили нашу самодельную систему импульсно-пространственной спектроскопии на основе Фурье-оптики 43 для получения поляризационно-зависимого угла -разрешенные спектры пропускания.На рисунке 3а показаны измеренные спектры вдоль направления Γ-X при падении с круговой поляризацией. Уменьшенная точка провалов коэффициента пропускания, отмеченная красной (синей) стрелкой, соответствует моде излучения правой (левой) круговой поляризации на полосе TE 2 .
 Положение и направленность мод с круговой поляризацией соответствуют смоделированной карте поляризации. Принимая во внимание фактические спектры, показанные на рис. 3а, мы выбираем целевую длину волны 816 нм.Кроме того, мы экспериментально измерили фазовые распределения в кросс-поляризованном импульсном пространстве после взаимодействия с пластиной PhC, как показано на рис. 3b, с помощью нашей системы измерения фаз 39 . Измеренные фазовые распределения хорошо согласуются с нашими результатами моделирования и показывают ожидаемые результирующие фазовые градиенты в направлении k x .
Положение и направленность мод с круговой поляризацией соответствуют смоделированной карте поляризации. Принимая во внимание фактические спектры, показанные на рис. 3а, мы выбираем целевую длину волны 816 нм.Кроме того, мы экспериментально измерили фазовые распределения в кросс-поляризованном импульсном пространстве после взаимодействия с пластиной PhC, как показано на рис. 3b, с помощью нашей системы измерения фаз 39 . Измеренные фазовые распределения хорошо согласуются с нашими результатами моделирования и показывают ожидаемые результирующие фазовые градиенты в направлении k x .Рис. 3: Экспериментально измеренные фотонные полосы и фазовые распределения, индуцированные PhC.
a Измеренные спектры пропускания с угловым разрешением пластины PhC с падающим лучом с правой круговой поляризацией (RCP) (слева) и с левой круговой поляризацией (LCP) (справа).Фотонные полосы пластины PhC проявляются в виде провалов в спектрах.
 Мода с собственным состоянием поляризации LCP (RCP), отмеченная синей (красной) стрелкой, не будет реагировать на возбуждение RCP (LCP) и окажется уменьшенной точкой среди полосовых сигналов. b Измеренные фазовые распределения, вызванные кросс-поляризованным преобразованием пластины PhC на длине волны 816 нм. Падающая и анализируемая поляризации на левой (правой) панели равны \(\left|+45\right\rangle\) (\(\left|-45\right\rangle\)) и \(\left\langle — 45\вправо|\) (\(\влево\лангл +45\вправо|\)) соответственно. c Фазовые распределения вдоль линий, отмеченных b . Сплошные (штриховые) кривые на левой и правой панелях показывают фазовые распределения вдоль сплошных (штриховых) линий на левой и правой панелях b соответственно.
Мода с собственным состоянием поляризации LCP (RCP), отмеченная синей (красной) стрелкой, не будет реагировать на возбуждение RCP (LCP) и окажется уменьшенной точкой среди полосовых сигналов. b Измеренные фазовые распределения, вызванные кросс-поляризованным преобразованием пластины PhC на длине волны 816 нм. Падающая и анализируемая поляризации на левой (правой) панели равны \(\left|+45\right\rangle\) (\(\left|-45\right\rangle\)) и \(\left\langle — 45\вправо|\) (\(\влево\лангл +45\вправо|\)) соответственно. c Фазовые распределения вдоль линий, отмеченных b . Сплошные (штриховые) кривые на левой и правой панелях показывают фазовые распределения вдоль сплошных (штриховых) линий на левой и правой панелях b соответственно.Боковые смещения луча в реальном пространстве затем непосредственно наблюдаются с помощью системы формирования изображений в реальном пространстве (подробности см. в Дополнительном примечании 8). Как и при измерении фазы, один линейный поляризатор размещается с каждой стороны плоскости образца для контроля падающей и анализируемой поляризаций.
 Поляризация поляризатора падения и анализатора настроена на \(\left|+45\right\rangle\) и \(\left\langle -45\right|\), соответственно (\(\left|-45 \right\rangle\) и \(\left\langle +45\right|\) для другого случая). В последующих измерениях они не будут вращаться, чтобы избежать искусственных ошибок. Гауссовский световой пучок с длиной волны 816 нм от перестраиваемого лазера затем фокусируется на плоскости образца при нормальном падении, проходя через диафрагму на передней плоскости Фурье фокусирующей линзы, чтобы ограничить распределение луча k ∥ (расхождение угол).Радиус перетяжки луча (определяемый положением, в котором интенсивность 1/ e 2 максимальна) составляет около 4,1 мкм. После анализа анализатором распределение интенсивности исходящего луча фиксируется устройством с зарядовой связью (ПЗС), что позволяет нам непосредственно наблюдать за лучом.
Поляризация поляризатора падения и анализатора настроена на \(\left|+45\right\rangle\) и \(\left\langle -45\right|\), соответственно (\(\left|-45 \right\rangle\) и \(\left\langle +45\right|\) для другого случая). В последующих измерениях они не будут вращаться, чтобы избежать искусственных ошибок. Гауссовский световой пучок с длиной волны 816 нм от перестраиваемого лазера затем фокусируется на плоскости образца при нормальном падении, проходя через диафрагму на передней плоскости Фурье фокусирующей линзы, чтобы ограничить распределение луча k ∥ (расхождение угол).Радиус перетяжки луча (определяемый положением, в котором интенсивность 1/ e 2 максимальна) составляет около 4,1 мкм. После анализа анализатором распределение интенсивности исходящего луча фиксируется устройством с зарядовой связью (ПЗС), что позволяет нам непосредственно наблюдать за лучом.Сначала мы вставляем неструктурированное Si 3 N 4 окно той же толщины, что и плита из PhC, в плоскость образца.
 Несмотря на ортогональность поляризатора и анализатора, ограниченный коэффициент ослабления поляризаторов позволяет передавать очень небольшую часть луча без кросс-поляризованного преобразования.Таким образом, мы можем найти исходный луч и установить нули координат. На рисунке 4а показано нормализованное распределение интенсивности исходного прошедшего светового луча. Впоследствии мы переключаем образец на изготовленную плиту PhC. Как показано на рис. 4b, измеряется нормализованная интенсивность кросс-поляризованного луча. Поперечные сдвиги луча можно наблюдать непосредственно. Направления смещения луча согласуются с нашими теоретическими предсказаниями. На рис. 4в представлены распределения интенсивности вдоль линий, отмеченных на рис.4а, б, из которых мы можем сказать, что сдвиг пика интенсивности составляет около 4,2 мкм, что согласуется с оценочным сдвигом (около 4,3 мкм) от среднего фазового градиента, рассчитанного по измеренным фазовым картам (рис. 3б). Сдвиги четко наблюдаются, подтверждая наше предположение.
Несмотря на ортогональность поляризатора и анализатора, ограниченный коэффициент ослабления поляризаторов позволяет передавать очень небольшую часть луча без кросс-поляризованного преобразования.Таким образом, мы можем найти исходный луч и установить нули координат. На рисунке 4а показано нормализованное распределение интенсивности исходного прошедшего светового луча. Впоследствии мы переключаем образец на изготовленную плиту PhC. Как показано на рис. 4b, измеряется нормализованная интенсивность кросс-поляризованного луча. Поперечные сдвиги луча можно наблюдать непосредственно. Направления смещения луча согласуются с нашими теоретическими предсказаниями. На рис. 4в представлены распределения интенсивности вдоль линий, отмеченных на рис.4а, б, из которых мы можем сказать, что сдвиг пика интенсивности составляет около 4,2 мкм, что согласуется с оценочным сдвигом (около 4,3 мкм) от среднего фазового градиента, рассчитанного по измеренным фазовым картам (рис. 3б). Сдвиги четко наблюдаются, подтверждая наше предположение. Обратите внимание, что общий сдвиг луча без анализатора будет менее очевидным, так как в эксперименте только 12% падающей мощности преобразуется в проходящий кросс-поляризованный пучок. Результаты без анализа включены в дополнительное примечание 9.Мы также включаем другие результаты на разных длинах волн в Дополнительное примечание 10.
Обратите внимание, что общий сдвиг луча без анализатора будет менее очевидным, так как в эксперименте только 12% падающей мощности преобразуется в проходящий кросс-поляризованный пучок. Результаты без анализа включены в дополнительное примечание 9.Мы также включаем другие результаты на разных длинах волн в Дополнительное примечание 10.Рис. 4: Экспериментально наблюдаемые боковые сдвиги, зависящие от поляризации.
a Нормированные распределения интенсивности исходного луча, проходящего через неструктурированное окно Si 3 N 4 после двух установок кросс-поляризованного анализа. На графиках отмечены состояния падающей поляризации, а анализируемые поляризации ортогональны падающей поляризации.Положения центров лучей задаются как нули координат. b Нормированные распределения интенсивности пучка, прошедшего через изготовленную плиту ФХ после двух установок кросс-поляризованного анализа. Состояние падающей поляризации для каждой панели такое же, как у и .
 c Нормализованные распределения интенсивности наблюдаемых лучей вдоль оси x , срезы a и b . Пунктирные зеленые кривые соответствуют исходным лучам, показанным в a , тогда как сплошные оранжевые кривые соответствуют смещенным лучам, показанным в b , соответственно.Двунаправленная стрелка отмечает лучевую талию.
c Нормализованные распределения интенсивности наблюдаемых лучей вдоль оси x , срезы a и b . Пунктирные зеленые кривые соответствуют исходным лучам, показанным в a , тогда как сплошные оранжевые кривые соответствуют смещенным лучам, показанным в b , соответственно.Двунаправленная стрелка отмечает лучевую талию.Подчеркнем, что наш подход к реализации больших сдвигов луча основан на нелокальных резонансах, поддерживаемых пластиной PhC. Это приводит к тому преимуществу, что любая область плиты PhC может использоваться для смещения произвольного количества лучей одновременно. Кроме того, в отличие от громоздких традиционных подходов, которые направляют световые лучи с помощью тщательно выровненных рефракторов и отражателей, наш подход может перемещать лучи точно в пределах нескольких сотен нанометров в направлении их распространения без изменения направления.Это делает пластину PhC вполне подходящей для разводки света в компактных устройствах.

В заключение мы представили метод реализации латеральных сдвигов за счет использования структуры импульсно-пространственной поляризации пластин PhC. Градиенты геометрической фазы в импульсном пространстве вводятся в световые лучи за счет кросс-поляризованного преобразования, происходящего в пластинах PhC, и экспериментально наблюдались большие латеральные сдвиги при нормальном падении. Мы предполагаем, что структура импульсно-пространственной поляризации пластин PhC может работать как новая степень свободы для управления световыми лучами.Между тем, наши результаты вдохновляют на исследование и модуляцию световых лучей в реальном пространстве с точки зрения импульсного пространства.
Ионные пучки из плазмы: от космоса до нанотехнологий
Ионные пучки, полученные из плазмы, произвели революцию во многих областях физики и приложений. Одной из ключевых областей за последние несколько десятилетий была обработка полупроводников для изготовления интегральных схем, где направленные ионные пучки, полученные из плазмы, помогали вытравливать элементы размером от микрона до субмикрона.
 ..
..Ионные пучки, полученные из плазмы, произвели революцию во многих областях физики и приложений. Одной из ключевых областей за последние несколько десятилетий была обработка полупроводников для изготовления интегральных схем, где направленные ионные пучки, полученные из плазмы, помогали вытравливать микронные и субмикронные элементы с высоким соотношением сторон. Ионно-лучевое травление с помощью плазмы стало движущей силой полупроводниковой промышленности.Исторически сложилось так, что ионные пучки, полученные из электронно-циклотронной резонансной плазмы, были чрезвычайно полезны в основных исследованиях ядерной физики и преобладают в большинстве ядерно-физических лабораторий по всему миру, где интенсивные многозарядные ионы ускорялись до высоких энергий и использовались как в традиционной ядерной физике. эксперименты в качестве снарядов и для создания пучков радиоактивных ионов. Ускоренные пучки после прохождения через циклотрон уже много лет применяются в медицине для лечения рака.
 В последние одно-два десятилетия еще одной областью, которой уделяется значительное внимание, являются технологии космических двигателей, использующие ионные пучки от плазменных источников. Были разработаны различные плазменные двигатели для движения электрических космических аппаратов с целью уменьшить полезную нагрузку ракеты за счет отказа от использования твердого и жидкого топлива и с целью облегчения футуристических межпланетных путешествий на большие расстояния. Есть несколько других новых областей, в которых ионные пучки из плазмы играют решающую роль в расширении границ исследований.Одной из таких областей является нано-микроструктурирование на основе сфокусированного ионного пучка (FIB). Обычные системы FIB на основе жидких металлов полагаются на галлий в качестве источника ионов, который представляет собой жидкий металл при комнатной температуре. Источники FIB на основе Ga страдают от проблем с поверхностным загрязнением. Кроме того, из-за меньших токов им требуется огромное время измельчения даже для измельчения небольшого объема.
В последние одно-два десятилетия еще одной областью, которой уделяется значительное внимание, являются технологии космических двигателей, использующие ионные пучки от плазменных источников. Были разработаны различные плазменные двигатели для движения электрических космических аппаратов с целью уменьшить полезную нагрузку ракеты за счет отказа от использования твердого и жидкого топлива и с целью облегчения футуристических межпланетных путешествий на большие расстояния. Есть несколько других новых областей, в которых ионные пучки из плазмы играют решающую роль в расширении границ исследований.Одной из таких областей является нано-микроструктурирование на основе сфокусированного ионного пучка (FIB). Обычные системы FIB на основе жидких металлов полагаются на галлий в качестве источника ионов, который представляет собой жидкий металл при комнатной температуре. Источники FIB на основе Ga страдают от проблем с поверхностным загрязнением. Кроме того, из-за меньших токов им требуется огромное время измельчения даже для измельчения небольшого объема. Чтобы удовлетворить возникающие области исследований, такие как обработка биоматериалов и микрофлюидные приложения, где в промышленности требуется высокая пропускная способность, предпринимаются усилия по разработке источников сфокусированного ионного пучка из газообразной плазмы инертных газов, которые могут быть неэффективными. -токсичен, поэтому подходит для биоматериалов.Кроме того, они обеспечат возможность быстрой обработки за счет более высоких токов без металлического загрязнения. В последние годы еще одной целевой областью, в которой наблюдается широкая активность, являются низкоэнергетические ионные пучки на основе плазмы для модификации поверхности материалов и добавления к ним большей функциональности. Ионные пучки низкой энергии применялись для создания атомарно-гетерогенных систем, в которых ионы входят в решетку-хозяин и ограничиваются несколькими подповерхностными слоями, тем самым создавая неоднородность на атомном уровне.Они изменяют поверхность (смачиваемость), электрические и оптические свойства материалов.
Чтобы удовлетворить возникающие области исследований, такие как обработка биоматериалов и микрофлюидные приложения, где в промышленности требуется высокая пропускная способность, предпринимаются усилия по разработке источников сфокусированного ионного пучка из газообразной плазмы инертных газов, которые могут быть неэффективными. -токсичен, поэтому подходит для биоматериалов.Кроме того, они обеспечат возможность быстрой обработки за счет более высоких токов без металлического загрязнения. В последние годы еще одной целевой областью, в которой наблюдается широкая активность, являются низкоэнергетические ионные пучки на основе плазмы для модификации поверхности материалов и добавления к ним большей функциональности. Ионные пучки низкой энергии применялись для создания атомарно-гетерогенных систем, в которых ионы входят в решетку-хозяин и ограничиваются несколькими подповерхностными слоями, тем самым создавая неоднородность на атомном уровне.Они изменяют поверхность (смачиваемость), электрические и оптические свойства материалов. Было обнаружено, что от локализованной подповерхностной имплантации в микронном масштабе до облучения большой площади ливневыми ионными пучками, изменяя плотность потока пучка и ионные частицы, можно реализовать широко настраиваемые свойства материала.
Было обнаружено, что от локализованной подповерхностной имплантации в микронном масштабе до облучения большой площади ливневыми ионными пучками, изменяя плотность потока пучка и ионные частицы, можно реализовать широко настраиваемые свойства материала.С приведенным выше обзором темы исследования потенциальные авторы могут представить высококачественные исследовательские работы в экспериментальных, теоретических и вычислительных областях или в их комбинации, чтобы они относились к широкой теме исследований ионных пучков из плазмы и их приложений от космоса до нанотехнологий.Объем не может быть ограничен только вышеупомянутыми темами, если представленная статья подпадает под действие заголовка. Мы приветствуем представление оригинальных исследований, обзоров, кратких отчетов об исследованиях и перспективных статей. Более подробную информацию о типах статей можно найти в руководстве для авторов.
Ключевые слова :
плазменные оболочки, экстракция, ускорение и фокусировка, ток и напряжение пучка, взаимодействие ионов с веществом, космическая тягаВажное примечание :
Все вклады в эту тему исследования должны быть в рамках раздела и журнала, в который они представлены, как это определено в их заявлениях о миссии. Frontiers оставляет за собой право направить рукопись, выходящую за рамки рассмотрения, в более подходящий раздел или журнал на любом этапе рецензирования.
Frontiers оставляет за собой право направить рукопись, выходящую за рамки рассмотрения, в более подходящий раздел или журнал на любом этапе рецензирования.Криштиану Роналду сияет: «Я всегда счастлив, когда возвращаюсь в свою страну», когда звезда сборной Португалии уходит от проблем «Манчестер Юнайтед».
36-летний нападающий смог забыть о проблемах с «Манчестер Юнайтед» во время тренировки с национальной сборной.
3
Криштиану Роналду позирует для фото с ПепеКредит: Instagram @Cristiano
3
Роналду явно развлекается на тренировке в ПортугалииКредит: AFP чтобы увеличить свой рекордный международный счет голов против Ирландии и Сербии.
Неудивительно, что он улыбается от уха до уха на фотографиях, которые он разместил в своих аккаунтах в социальных сетях.
В Твиттере он опубликовал фотографию, на которой он позирует с поднятыми большими пальцами на сборах в Португалии.
А рядом с фотографией он разместил подпись: «Доброе утро.
 Это всегда дополнительное счастье, когда я снова в своей стране!»
Это всегда дополнительное счастье, когда я снова в своей стране!»Тем временем в Instagram CR7 поделился снимком, на котором он усердно работает на тренировке.
Он также позировал перед камерой вместе с давним товарищем по команде и другом Пепе и подписал свой пост: «Готов к завтрашнему дню! #letgowitheverything».
Самые читаемые в Премьер-лиге
БЕСПЛАТНЫЕ СТАВКИ: ПОЛУЧИТЕ БОЛЕЕ 2000 ФУНТОВ В НОВЫХ СДЕЛКАХ ДЛЯ КЛИЕНТОВ
Португалия в настоящее время занимает второе место в отборочной группе чемпионата мира по футболу, но может обогнать лидера группы Сербию, если они обыграют их в воскресенье.
Команда Роналду не проигрывает в квалификации, и он будет полон решимости пройти квалификацию на еще один чемпионат мира после разочаровывающего Евро-2020, когда они вылетели во втором раунде.
CR7 также надеется вернуть чувство победы после неудачных результатов с United.
В прошлый раз он едва получил удар в матче с «Манчестер Сити» и не будет доволен тем, что выпал из четверки лучших, поскольку «красные дьяволы» сейчас на шесть очков отстают от «Сити», занявшего четвертое место.

⚽ Читайте наш блог Футбольные новости в прямом эфире , чтобы быть в курсе последних слухов, сплетен и заключенных сделок
определение балок по The Free Dictionary
балка
(bēm) n.
1. Прямоугольное бревно или большой продолговатый кусок дерева, металла или камня, используемый в основном в качестве горизонтальной опоры в строительстве.
2. Морской
а. Поперечный конструктивный элемент каркаса корабля, используемый для поддержки палубы и защиты бортов от напряжения.
б. Ширина корабля в самом широком месте.
в. Борт корабля: видна земля за правым лучом.
3. Неформальный Самая широкая часть бедер человека: широкая в пучок.
4. Стальная трубка или деревянный ролик, на который наматывается основа на ткацком станке.
5. Качающийся рычаг, соединенный со штоком поршня двигателя и используемый для передачи мощности на коленчатый вал.

6.
а. Штанга весов, к которой подвешиваются чаши для взвешивания.
б. Спорт Балансир.
7. Основной горизонтальный брус плуга, к которому крепятся лапа, сошник и рукояти.
8. Один из основных стеблей рога оленя.
9.
а. Луч или луч света.
б. Концентрированный поток частиц или подобное распространение волн: пучок протонов; луч света.
10. Радиолуч.
v. лучевой , лучевой , лучевой
v. вн.
1. Излучать свет; светить.
2. Широко улыбаться.
т. тр.
1. Для отправки или передачи: передать сообщение через спутник.
2. Выразить лучезарной улыбкой: Он сиял одобрением новой идеи.
Идиома: по лучу
1. По радиолучу. Используется в самолетах.
2. На правильном пути; работает правильно.

Словарь английского языка American Heritage®, пятое издание. Авторские права © 2016, издательство Houghton Mifflin Harcourt Publishing Company. Опубликовано издательством Houghton Mifflin Harcourt Publishing Company. Все права защищены.
балка
(двухметровая) n
1. (здание) длинный толстый прямоугольный кусок дерева, металла, бетона и т. д., особенно используемый в качестве горизонтального элемента конструкции
2. (общее машиностроение) любой жесткий элемент или конструкция, нагруженная поперечно свет, как от маяка
5. широкая улыбка
6. (Поделки) один из двух цилиндрических роликов на станке, один из которых удерживает нити основы перед ткачеством, другой — готовую работу
7. (Зоология) основной стержень рога оленя, из которого растут более мелкие ветви
8. (Сельское хозяйство) центральный вал плуга, к которому крепятся все основные части
9.
 (Общая физика) узкий однонаправленный поток электромагнитного излучения или частиц: пучок света; электронный пучок.
(Общая физика) узкий однонаправленный поток электромагнитного излучения или частиц: пучок света; электронный пучок.10. (общая физика) горизонтальная центрально-поворотная штанга в равновесии
11. (анатомия) неформальная ширина бедер (особенно в словосочетании широкая в луче )
9
3
3 12. бревно в глазу ошибка или серьезная ошибка, большая в себе, чем в другом человеке , или не имеет значения
15. (Навигация) по радиолучу для удержания курса
16. (Морские термины) Морской против траверза судна; на траверзе
17. неформальный правильный, актуальный или подходящий
vb
18. посылать или излучать (лучи света)
19. (вещание) ( 4 tr) отклонять радио ( 4 tr) сигнал или трансляция, свет и т. д.) в определенном направлении: передать программу в Токио.
20. (Информатика) для передачи (данных, особенно данных визитных карточек и т.
 д.) с одного карманного компьютера на другой с помощью инфракрасных лучей
д.) с одного карманного компьютера на другой с помощью инфракрасных лучей21. ( intr ) широко улыбаться от удовольствия или удовлетворения
[ древнеанглийское beam ; Связанные с Gothic Bagms Дерево , Старый Высокий Немецкий BUM Дерево
Лучшие
Луча
- , N
Beambloble ADJ
Beamˌlike ADJ
SIGY ADJ
Collins English Persontionary — полное и ненабженное, 12-е издание 2014 © Harpercollins Publishers 1991, 1994, 1998, 2000, 2003, 2006, 2007, 2009, 2011, 2014, 2014 г.
Beam
( бим)
н.1. любые относительно длинные куски металла, дерева и т. д., бывшие в употреблении, особ. как жесткие элементы или части конструкций или машин.
2. горизонтальный несущий элемент в виде балки или перемычки или поперечный поддерживающий элемент конструкции на корабле.

3. максимальная ширина корабля.
4. Сленг. мерка по обеим бедрам или ягодицам.
5.
а. (в ткацком станке) ролик или цилиндр, на который наматывается основа перед ткачеством.
б. аналогичный цилиндр, на который наматывается ткань по мере ее ткачества.
6. поперечина весов, к которой подвешиваются весы или чашки.
7. луч или поток света или другое излучение, такое как гамма-лучи, электроны или субатомные частицы.
8. группа почти параллельных лучей.
9. радиосигнал, передаваемый по узкому курсу, используемый для наведения пилотов.
10. сияющая улыбка.
11. основной ствол рога оленя.
в.т.
12. излучать в или как бы в лучах или лучах.
13. для передачи (радио- или телевизионного сигнала) в определенном направлении.
14. направить (радио- или телевизионную программу, коммерческое сообщение и т.
 д.)) для заранее определенной аудитории.
д.)) для заранее определенной аудитории.в.и.
15. испускать лучи, как свет.
16. улыбаться лучезарно или счастливо.
Идиомы: на балке,
а. по курсу, указанному радиолучом.
б. Неофициальный. правильно; точный.
[до 900; Среднеанглийский beem, Древнеанглийский beem дерево, столб, луч света, c.Старофризский bām, Древневерхненемецкий boum, Древнескандинавский Bathmr ]
Random House Словарь Kernerman Webster’s College Dictionary, © 2010 K Dictionaries Ltd. Copyright 2005, 1997, 1991 Random House, Inc. Все права защищены.
Лучшие бревна 2022 года
Руководство по покупке балансиров
Мы все с трепетом смотрим на выступления профессиональных гимнасток и чирлидеров.Их нежные, но ловкие маневры, элегантные прыжки и прыжки, а также то, как они скользят по различным платформам, настолько необычны, что даже медузы могли бы ими гордиться.
 Однако этот уровень изящества и чутья не дается легко; это требует таланта, постоянной практики и многих тяжелых падений.
Однако этот уровень изящества и чутья не дается легко; это требует таланта, постоянной практики и многих тяжелых падений.В какой-то момент своей карьеры каждый профессиональный гимнаст сталкивался с бревном. Это простое, но динамичное устройство, которым должен владеть каждый акробат, чтобы совершенствовать и развивать свои навыки. Балансиры также будут задействованы во время соревнований, поэтому профессиональные и будущие гимнасты должны быть с ними знакомы.
Балансир найдется для любого возраста, опыта и навыков, поэтому вам не стоит беспокоиться о дефиците. О чем вам следует беспокоиться, так это о выборе наилучшего балансира. И с таким количеством вариантов на рынке выбрать идеальное бревно может быть непросто. Это руководство по покупке облегчает задачу, предлагая конкретные характеристики, на которые следует обращать внимание при покупке балансира.
Факторы, которые следует учитывать при покупке балансира
Балансиры бывают разных форм и размеров, и лучшие из них обладают функциями, которых нет у других.
 Вы должны учитывать некоторые ключевые факторы, чтобы получить наилучшее впечатление от гимнастики. Они могут спасти вас от травм или вреда, поэтому давайте обсудим их ниже.
Вы должны учитывать некоторые ключевые факторы, чтобы получить наилучшее впечатление от гимнастики. Они могут спасти вас от травм или вреда, поэтому давайте обсудим их ниже.С какого возраста дети могут начать пользоваться бревном?
Дети должны учиться балансу, моторике и ловкости с раннего возраста, и это не обязательно имеет какое-либо отношение к гимнастике. Балансиры безопасны и идеально подходят для детей чуть старше 12 месяцев, но вы должны выбрать правильный вариант для этой возрастной группы. Для оптимальной безопасности выберите балансир, который находится всего в дюйме или двух от земли, или, что еще лучше, используйте балансиры на земле.Эти опции сделают падение менее опасным и болезненным. Низкая высота луча также устранит фактор страха и позволит вашему ребенку уверенно ходить или играть.
Какие бывают типы балансиров?
Балансиры делятся на категории в зависимости от того, насколько далеко они находятся от уровня земли, что является важным фактором, определяющим возраст и уровень навыков, для которых они предназначены.

Наземные балансиры
Как следует из названия, эти балки перекрытия непосредственно соприкасаются с полом.И причина такой конструкции без высоты не надуманная — это защита детей или любителей от серьезных травм при падении. В дополнение к небольшой высоте балансиры на земле также имеют сердцевину из мягкого пеноматериала и деликатные материалы поверхности, такие как замша или кожа.
Внеземные балансиры
Двигаясь вверх по спектру, у нас есть балансирные балки, расположенные вне земли. Они рассчитаны на чуть более опытных гимнасток, поэтому часто изготавливаются из дерева и немного приподняты над землей.Эти балки предлагают более высокое чувство конкуренции, но падение с них может быть довольно болезненным. Поэтому, если вы пробуете новые навыки или часто падаете, вам следует избегать этих моделей.
Усовершенствованные балансиры высоты
Эти модели бревна предназначены для профессиональных спортсменов и довольно часто используются в элитных спортивных сооружениях, где проводятся соревнования.
 Они далеко от земли (до 4,1 метра), что делает их сложными, но интригующими для исполнения.
Они далеко от земли (до 4,1 метра), что делает их сложными, но интригующими для исполнения.Из чего сделаны балансиры?
Балансировочные бревна для взрослых и опытных спортсменов часто имеют деревянную основу, но это не должен быть единственный элемент, из которого состоит бревно.Другими словами, избегайте балок с голыми деревянными поверхностями, какими бы полированными или украшенными они ни были. Такие бревна были запрещены с конца 90-х годов, потому что они скользкие и представляют опасность для спортсменов, которые на них выступают. Другие бревна для детей и гимнастов-любителей имеют сердцевину из мягкого пеноматериала с резиновой подкладкой, которая не причинит много травм при падении.
Однако независимо от того, из чего сделан балансир, он всегда должен быть покрыт или обернут синтетическими материалами, такими как замша, EVA, винил или кожа.Все они обеспечивают хорошее сцепление и трение, тем самым значительно снижая угрозу скольжения. Тем не менее, вы должны знать, что замшевые балансиры более устойчивы к разрывам, чем другие варианты, поэтому вы можете учитывать это при покупке бревна.

Должны ли балансиры быть легкими?
Легкие балансиры являются лучшими. Их легко упаковывать, носить с собой и убирать в сторону даже детям. Это сэкономит вам много стресса и времени, поэтому убедитесь, что вы выбрали легкие балансиры. Обратите внимание, что лучшие балансиры никогда не жертвуют стабильностью или безопасностью ради легкости.Поэтому при выборе балансира убедитесь, что он легкий, устойчивый и прочный.
Что придает бревнам такую устойчивость?
Лучшие бревна стабильны и способны выдерживать вес и движения гимнасток, не падая, благодаря прочному основанию. Чтобы выбрать действительно устойчивую балку, проверьте и убедитесь, что она имеет широкое основание около 6 дюймов, жесткое шарнирное соединение и противоскользящее основание. Низкокачественные балансиры могут иметь скользкое или плохо сконструированное дно.Избежать их. Для непревзойденной устойчивости выбирайте балансиры с основанием на липучке.
Складные балансиры лучше?
Представьте себе балансир, который не только легкий, но и портативный.
 Блаженство. Складные бревна всегда лучше, потому что вы можете легко упаковать их в чехол для хранения и взять с собой в спортзал или на отдых или в поход. Некоторые жесткие балансиры также мобильны, но их сложно упаковать, транспортировать и установить.
Блаженство. Складные бревна всегда лучше, потому что вы можете легко упаковать их в чехол для хранения и взять с собой в спортзал или на отдых или в поход. Некоторые жесткие балансиры также мобильны, но их сложно упаковать, транспортировать и установить.Все ли балки пола водонепроницаемы?
Не все балансиры водонепроницаемы, но вы должны приобрести такой.Вы можете использовать водонепроницаемые водяные балки на открытом воздухе, когда они влажные, не беспокоясь о деградации или намокании. Водонепроницаемые балки пола спроектированы так, чтобы не скользить во влажном состоянии, чтобы вы или ваши дети могли хорошо провести время, катаясь на лодке под дождем.
Подъемные балки и траверсы от Fyns Kran Udstyr
Часто задаваемые вопросы о подъемных балках и траверсах
Срок поставки подъемных траверс и траверс?
У нас есть очень быстрая доставка для нашей основной программы, которая состоит из подъемных балок S10, S11 и h20, а также траверсы S20, так как мы производим их в Дании. Для специально разработанных подъемных балок и траверс-распорок это будет различаться в зависимости от типа балки, но, поскольку мы разрабатываем и производим сами, мы часто можем предложить быстрые сроки поставки и для траверс специальной конструкции.
Для специально разработанных подъемных балок и траверс-распорок это будет различаться в зависимости от типа балки, но, поскольку мы разрабатываем и производим сами, мы часто можем предложить быстрые сроки поставки и для траверс специальной конструкции.Цены на подъемные балки и траверсы?
Ваш личный логин дает вам доступ к вашим фактическим ценам, которые вы можете увидеть сразу. Если у вас есть особые вопросы, мы вышлем вам предложение и 3D-чертежи как можно скорее, чтобы вы могли визуализировать свое окончательное решение, прежде чем принять решение.Можно ли арендовать траверсы и траверсы в Fyns Kran Udstyr?
ДА вы можете – и это очень просто. Если вы знаете, что подъемная траверса или распорная траверса предназначена для использования всего пару раз, зачастую проще взять ее напрокат, чем купить. Узнайте больше об аренде подъемных и распорных балок и другой продукции в Fyns Kran Udstyr здесь.Вы производите подъемные и распорные траверсы специальной конструкции?
ДА мы делаем — мы производим подъемные и разбрасывающие балки для любых целей, а с 1969 года мы проектировали и изготавливали множество различных типов балок для наших клиентов по всему миру.


 com
com Никаких инвесторов, только наш собственный успех. Мы олицетворяем классический успех на среднем рынке благодаря творчеству нашей целеустремленной команды.
Никаких инвесторов, только наш собственный успех. Мы олицетворяем классический успех на среднем рынке благодаря творчеству нашей целеустремленной команды. {2}}\).
{2}}\). Как пара обратных пространств, световые поля реального пространства и импульсного пространства тесно коррелированы. Следовательно, \( < {{{{{{{\bf{R}}}}}}}} > \) и \( < {{{{{{{\bf{P}}}}}}}}} > 1) можно модулировать фазовыми распределениями в соответствующем обратном пространстве. Модуляции φ в реальном пространстве вызовут изменения на \( < {{{{{{\bf{P}}}}}}}}} > \), изменяя направление распространения. Исходя из этого принципа, аномальное отражение и преломление световых лучей метаповерхностями можно понимать как эффекты модулированных фазовых градиентов реального пространства 31 .Точно так же, если мы можем модулировать распределение фазы импульсного пространства ϕ , модуляция на \( < {{{{{{\bf{R}}}}}}}} > \) светового луча могут быть реализованы, т. е. световые лучи могут быть смещены в реальном пространстве. Как схематично показано на рис. 1а, если градиент фазы ввести в серию плоских волн, составляющих луч, результирующий новый луч будет смещаться в соответствии с градиентом фазы в направлении уменьшения дополнительной фазы.
Как пара обратных пространств, световые поля реального пространства и импульсного пространства тесно коррелированы. Следовательно, \( < {{{{{{{\bf{R}}}}}}}} > \) и \( < {{{{{{{\bf{P}}}}}}}}} > 1) можно модулировать фазовыми распределениями в соответствующем обратном пространстве. Модуляции φ в реальном пространстве вызовут изменения на \( < {{{{{{\bf{P}}}}}}}}} > \), изменяя направление распространения. Исходя из этого принципа, аномальное отражение и преломление световых лучей метаповерхностями можно понимать как эффекты модулированных фазовых градиентов реального пространства 31 .Точно так же, если мы можем модулировать распределение фазы импульсного пространства ϕ , модуляция на \( < {{{{{{\bf{R}}}}}}}} > \) светового луча могут быть реализованы, т. е. световые лучи могут быть смещены в реальном пространстве. Как схематично показано на рис. 1а, если градиент фазы ввести в серию плоских волн, составляющих луч, результирующий новый луч будет смещаться в соответствии с градиентом фазы в направлении уменьшения дополнительной фазы. Учитывая механизм, можно разместить пространственные модуляторы света в плоскостях Фурье классических оптических путей для искусственного смещения лучей.Обычные сдвиги светового луча, такие как хорошо известные сдвиги G-H и I-F, могут быть приписаны фазовым градиентам импульс-пространство, вызванным процессами отражения или преломления на границах раздела.
Учитывая механизм, можно разместить пространственные модуляторы света в плоскостях Фурье классических оптических путей для искусственного смещения лучей.Обычные сдвиги светового луча, такие как хорошо известные сдвиги G-H и I-F, могут быть приписаны фазовым градиентам импульс-пространство, вызванным процессами отражения или преломления на границах раздела.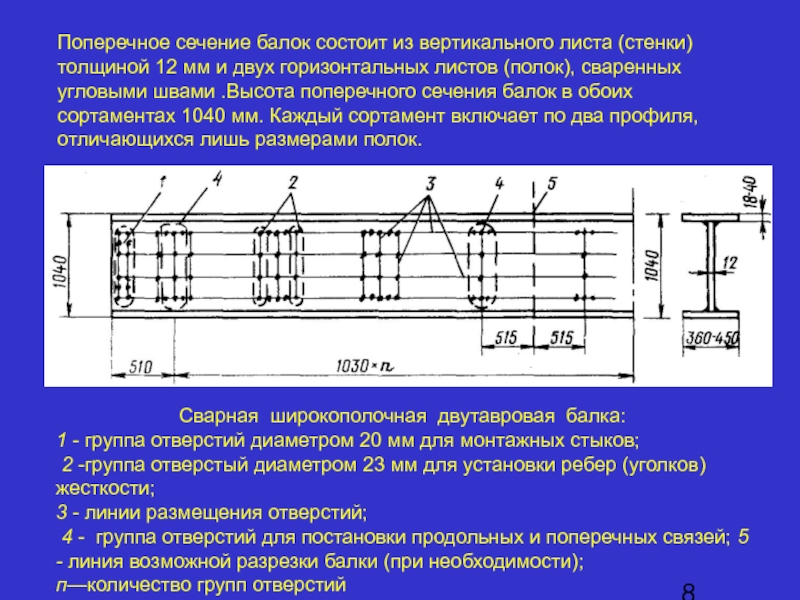 c Схематическое изображение бокового смещения, реализованного разработанной плитой PhC. \(\left|-45\right\rangle\) поляризованный луч светит нормально, и после процесса рассеяния рассеянное поле можно рассматривать как четыре рассеянных луча: прямо передающий и отражающий лучи и кросс-поляризационно преобразованный передающие и отражающие лучи. Преобразованные кросс-поляризацией лучи будут смещены в направлении, противоположном фазовому градиенту импульс-пространство.
c Схематическое изображение бокового смещения, реализованного разработанной плитой PhC. \(\left|-45\right\rangle\) поляризованный луч светит нормально, и после процесса рассеяния рассеянное поле можно рассматривать как четыре рассеянных луча: прямо передающий и отражающий лучи и кросс-поляризационно преобразованный передающие и отражающие лучи. Преобразованные кросс-поляризацией лучи будут смещены в направлении, противоположном фазовому градиенту импульс-пространство. Плиты PhC, которые имеют определяемые режимы излучения, состоящие из состояний фотонных полос 32,33,34,35,36 , являются идеальными платформами для выполнения модуляции света в импульсном пространстве 37,38,39,40 .Для пластины PhC ее излучательные резонансные моды с различными волновыми векторами в плоскости внутри светового конуса могут взаимодействовать с плоскими волнами в свободном пространстве из-за взаимности. Хотя моды имеют разные длины собственных волн, их утечка приводит к конечному времени жизни и, следовательно, к конечной ширине пика как длины волны, так и плоского волнового вектора. В результате монохроматический пучок конечного размера, состоящий из серии плоских волн, может возбудить резонансные моды, которые охватывают область в импульсном пространстве, даже если существует несоответствие длин волн.Благодаря связи компоненты падающего луча с определенными состояниями поляризации будут частично преобразованы в компоненты с ортогональными состояниями поляризации.
Плиты PhC, которые имеют определяемые режимы излучения, состоящие из состояний фотонных полос 32,33,34,35,36 , являются идеальными платформами для выполнения модуляции света в импульсном пространстве 37,38,39,40 .Для пластины PhC ее излучательные резонансные моды с различными волновыми векторами в плоскости внутри светового конуса могут взаимодействовать с плоскими волнами в свободном пространстве из-за взаимности. Хотя моды имеют разные длины собственных волн, их утечка приводит к конечному времени жизни и, следовательно, к конечной ширине пика как длины волны, так и плоского волнового вектора. В результате монохроматический пучок конечного размера, состоящий из серии плоских волн, может возбудить резонансные моды, которые охватывают область в импульсном пространстве, даже если существует несоответствие длин волн.Благодаря связи компоненты падающего луча с определенными состояниями поляризации будут частично преобразованы в компоненты с ортогональными состояниями поляризации. Геометрические фазовые изменения, зависящие от волнового вектора (фаза Панчаратнама-Берри или P-B 41,42 ), будут индуцироваться в кросс-поляризованных исходящих компонентах процессом преобразования в дополнение к фазовым изменениям, вызванным резонансом. Если дополнительно зафиксировать состояние поляризации падающего луча и анализируемое состояние поляризации выходящего луча как ортогональные, относительные значения фазовых изменений P–B будут определяться промежуточными собственными состояниями поляризации взаимодействующих резонансов.Можно видеть, что распределение собственных состояний поляризации в импульсном пространстве вводит соответствующее геометрическое фазовое распределение в луч с определенным процессом поляризации-анализа 38,39,40 . Управляя состояниями поляризации падающего и анализируемого луча и выбирая хорошо структурированную пластину PhC, мы можем спроектировать фазовое распределение анализируемого луча в импульсном пространстве и его градиент.
Геометрические фазовые изменения, зависящие от волнового вектора (фаза Панчаратнама-Берри или P-B 41,42 ), будут индуцироваться в кросс-поляризованных исходящих компонентах процессом преобразования в дополнение к фазовым изменениям, вызванным резонансом. Если дополнительно зафиксировать состояние поляризации падающего луча и анализируемое состояние поляризации выходящего луча как ортогональные, относительные значения фазовых изменений P–B будут определяться промежуточными собственными состояниями поляризации взаимодействующих резонансов.Можно видеть, что распределение собственных состояний поляризации в импульсном пространстве вводит соответствующее геометрическое фазовое распределение в луч с определенным процессом поляризации-анализа 38,39,40 . Управляя состояниями поляризации падающего и анализируемого луча и выбирая хорошо структурированную пластину PhC, мы можем спроектировать фазовое распределение анализируемого луча в импульсном пространстве и его градиент.
 Мы помечаем эти два линейных состояния поляризации как ‘кет \(\лево|+45\право\угол\) и \(\лево|-45\право\угол\), а соответствующие анализируемые состояния поляризации — это ‘бюстгалтеры \( \left\langle +45\right|\) и \(\left\langle -45\right|\) для упрощения обозначений.{i {{\Delta}}{\phi}_{\left|\pm 45\right\rangle}}, \\ {{\Delta}}{\phi} _{\left|\pm 45\right\ rangle } =\mp \left[\arg ({{{{{S}}}}}_{3}+i{{{{{S}}}}}_{1})-\frac{\pi {2}\справа].$$
Мы помечаем эти два линейных состояния поляризации как ‘кет \(\лево|+45\право\угол\) и \(\лево|-45\право\угол\), а соответствующие анализируемые состояния поляризации — это ‘бюстгалтеры \( \left\langle +45\right|\) и \(\left\langle -45\right|\) для упрощения обозначений.{i {{\Delta}}{\phi}_{\left|\pm 45\right\rangle}}, \\ {{\Delta}}{\phi} _{\left|\pm 45\right\ rangle } =\mp \left[\arg ({{{{{S}}}}}_{3}+i{{{{{S}}}}}_{1})-\frac{\pi {2}\справа].$$ Приведенное выше уравнение показывает, что профиль поля поляризации на рис.1б показано фазовое распределение P–B, в котором результирующий фазовый градиент {\parallel})}{\partial {{{{{{{{\boldsymbol{k}}}}}}}}}}_{\parallel}}\right\rangle\) в k x направление может быть получено, как показано на нижней панели рис. 1b. Как объясняется уравнением (2), этот искусственный фазовый градиент может вызвать сдвиг анализируемого луча в реальном пространстве. Например, нормально падающий \(\влево|\pm 45\вправо\угол\) луч будет иметь отрицательное (положительное) x -направленное смещение после соединения с спроектированной плитой и анализа с помощью \(\влево\ langle \mp 45\right|\) поляризатор, как показано на рис.1с.
Приведенное выше уравнение показывает, что профиль поля поляризации на рис.1б показано фазовое распределение P–B, в котором результирующий фазовый градиент {\parallel})}{\partial {{{{{{{{\boldsymbol{k}}}}}}}}}}_{\parallel}}\right\rangle\) в k x направление может быть получено, как показано на нижней панели рис. 1b. Как объясняется уравнением (2), этот искусственный фазовый градиент может вызвать сдвиг анализируемого луча в реальном пространстве. Например, нормально падающий \(\влево|\pm 45\вправо\угол\) луч будет иметь отрицательное (положительное) x -направленное смещение после соединения с спроектированной плитой и анализа с помощью \(\влево\ langle \mp 45\right|\) поляризатор, как показано на рис.1с.
 2b. Красные (синие) эллипсы соответствуют правосторонним (левосторонним) состояниям поляризации, а точки с круговой поляризацией мы отметили соответственно соответствующими цветными точками. Видно, что структура поляризации и нормированные третьи параметры Стокса ( S 3 / S 0 ) зеркально антисимметричны, а большие оси эллипсов поляризации в основном горизонтальны.Другими словами, нормированный третий параметр Стокса собственных состояний поляризации изменится с отрицательного на положительный в направлении k x , проходящем через линейно поляризованную линию ( S 3 / S 0 ≥== ), а нормализованный второй параметр Стокса ( S 2 / S 0 ) держится около нуля, как мы и ожидали. Это распределение поляризации — то, что нам нужно, чтобы вызвать градиенты геометрической фазы в импульсном пространстве для луча.
2b. Красные (синие) эллипсы соответствуют правосторонним (левосторонним) состояниям поляризации, а точки с круговой поляризацией мы отметили соответственно соответствующими цветными точками. Видно, что структура поляризации и нормированные третьи параметры Стокса ( S 3 / S 0 ) зеркально антисимметричны, а большие оси эллипсов поляризации в основном горизонтальны.Другими словами, нормированный третий параметр Стокса собственных состояний поляризации изменится с отрицательного на положительный в направлении k x , проходящем через линейно поляризованную линию ( S 3 / S 0 ≥== ), а нормализованный второй параметр Стокса ( S 2 / S 0 ) держится около нуля, как мы и ожидали. Это распределение поляризации — то, что нам нужно, чтобы вызвать градиенты геометрической фазы в импульсном пространстве для луча. 2: Результаты моделирования пластины PhC, примененной для реализации зависимых от поляризации боковых смещений.
2: Результаты моделирования пластины PhC, примененной для реализации зависимых от поляризации боковых смещений.  d Моделированное фазовое распределение, зависящее от волнового вектора, вызванное преобразованием \(\left|\pm 45\right\rangle\) в \(\left|\mp 45\right\rangle\) на длине волны 820 нм.Верхний график: \(\left|+45\right\rangle\) падение и \(\left\langle -45\right|\) анализ; нижний график: \(\left|-45\right\rangle\) падение и \(\left\langle +45\right|\) анализ. e Вид сверху ( z = -1,5 мкм) и поперечное сечение ( y = 0 мкм) реализованных латеральных сдвигов на 820 нм путем моделирования. Нормально падающий гауссовский луч имеет центр в точке ( x = 0, y = 0). Показаны только исходящие лучи с преобразованными состояниями поляризации путем применения анализирующих матриц Джонса \(\left\langle \mp 45\right|\) к смоделированным полям.Цветовая карта нормализована в соответствии с максимальной интенсивностью луча, делая насыщенным цвет поля внутри плиты, усиленный направленными резонансами. Для ясности мы отмечаем положения максимумов смещенных лучей вместо центроидов.
d Моделированное фазовое распределение, зависящее от волнового вектора, вызванное преобразованием \(\left|\pm 45\right\rangle\) в \(\left|\mp 45\right\rangle\) на длине волны 820 нм.Верхний график: \(\left|+45\right\rangle\) падение и \(\left\langle -45\right|\) анализ; нижний график: \(\left|-45\right\rangle\) падение и \(\left\langle +45\right|\) анализ. e Вид сверху ( z = -1,5 мкм) и поперечное сечение ( y = 0 мкм) реализованных латеральных сдвигов на 820 нм путем моделирования. Нормально падающий гауссовский луч имеет центр в точке ( x = 0, y = 0). Показаны только исходящие лучи с преобразованными состояниями поляризации путем применения анализирующих матриц Джонса \(\left\langle \mp 45\right|\) к смоделированным полям.Цветовая карта нормализована в соответствии с максимальной интенсивностью луча, делая насыщенным цвет поля внутри плиты, усиленный направленными резонансами. Для ясности мы отмечаем положения максимумов смещенных лучей вместо центроидов. Порядок графиков такой же, как у d .
Порядок графиков такой же, как у d . Принимая во внимание введенный нами основной принцип, можно реализовать зависящие от поляризации боковые сдвиги луча. Отметим, что на каждой из рассчитанных фазовых карт можно наблюдать фазовое искажение. Эти фазовые искажения вызваны динамическими фазовыми сдвигами, индуцированными резонансами, которые зеркально симметричны оси k y . Сдвиг луча нормально падающих лучей в направлении x должен быть результатом только геометрического фазового распределения из-за зеркальной симметрии.Подробное обсуждение резонансных фаз см. в дополнительном примечании 2 и примечании 5.
Принимая во внимание введенный нами основной принцип, можно реализовать зависящие от поляризации боковые сдвиги луча. Отметим, что на каждой из рассчитанных фазовых карт можно наблюдать фазовое искажение. Эти фазовые искажения вызваны динамическими фазовыми сдвигами, индуцированными резонансами, которые зеркально симметричны оси k y . Сдвиг луча нормально падающих лучей в направлении x должен быть результатом только геометрического фазового распределения из-за зеркальной симметрии.Подробное обсуждение резонансных фаз см. в дополнительном примечании 2 и примечании 5. 2в. Здесь, на рис. 2e, мы наносим изображения сверху в плоскости x — y вместе с видами поперечного сечения x = 0 смоделированных световых полей. Обратите внимание, что поля уже проанализированы кросс-поляризацией, так что можно увидеть только исходящий пучок, преобразованный резонансами, чтобы увидеть сдвиги луча, а поля без анализа включены в Дополнительное примечание 6 для сравнения. Около 43 % падающей мощности напрямую проходит через пластину, 23 % падающей мощности прямо отражается, 3 % теряется из-за конечного размера образца и около 15 % (15 %) падающей мощности преобразуется. в прошедший (отраженный) кросс-поляризованный пучок.Можно непосредственно наблюдать, что преобразованный пучок смещается влево ( x пик ~-4,6 микрона) в случае \(\left|+45\right\rangle\)-поляризованного падающего луча, и к правый ( x пик ~ 4,6 мкм) в другом случае (\(\left|-45\right\rangle\)-поляризованный). Результаты хорошо согласуются с нашим теоретическим предсказанием о том, что луч будет смещаться в сторону уменьшения фазы, которая контролируется поляризацией луча.
2в. Здесь, на рис. 2e, мы наносим изображения сверху в плоскости x — y вместе с видами поперечного сечения x = 0 смоделированных световых полей. Обратите внимание, что поля уже проанализированы кросс-поляризацией, так что можно увидеть только исходящий пучок, преобразованный резонансами, чтобы увидеть сдвиги луча, а поля без анализа включены в Дополнительное примечание 6 для сравнения. Около 43 % падающей мощности напрямую проходит через пластину, 23 % падающей мощности прямо отражается, 3 % теряется из-за конечного размера образца и около 15 % (15 %) падающей мощности преобразуется. в прошедший (отраженный) кросс-поляризованный пучок.Можно непосредственно наблюдать, что преобразованный пучок смещается влево ( x пик ~-4,6 микрона) в случае \(\left|+45\right\rangle\)-поляризованного падающего луча, и к правый ( x пик ~ 4,6 мкм) в другом случае (\(\left|-45\right\rangle\)-поляризованный). Результаты хорошо согласуются с нашим теоретическим предсказанием о том, что луч будет смещаться в сторону уменьшения фазы, которая контролируется поляризацией луча. Рассчитанный сдвиг луча для каждого случая примерно в 6 раз превышает длину волны и близок к радиусу перетяжки луча (~ 6 микрон).Будучи достаточно большими, смещения пучка хорошо видны и поэтому желательны для применения.
Рассчитанный сдвиг луча для каждого случая примерно в 6 раз превышает длину волны и близок к радиусу перетяжки луча (~ 6 микрон).Будучи достаточно большими, смещения пучка хорошо видны и поэтому желательны для применения.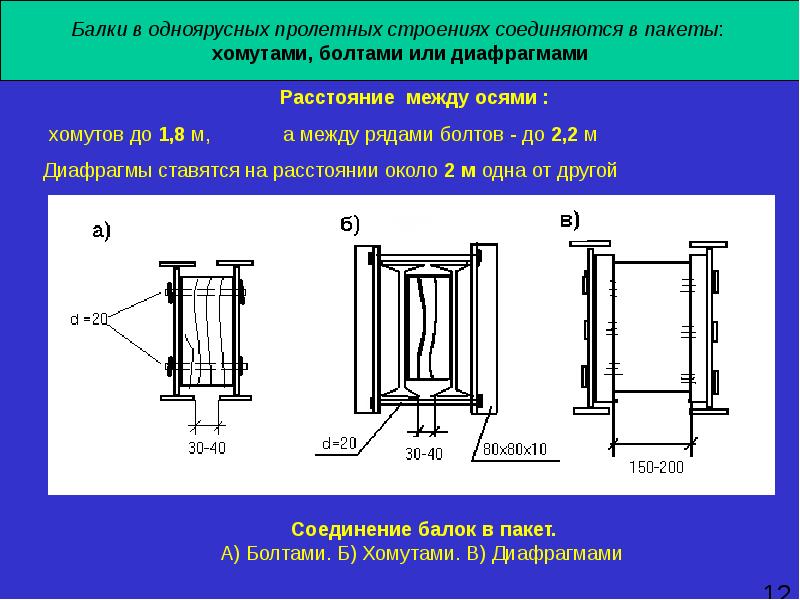 Все плоские структуры с той же симметрией, что и показанная, на самом деле имеют аналогичные структуры поляризации в импульсном пространстве 33,34,35,36 , и, таким образом, все они могут быть применены для реализации подобных сдвигов луча.
Все плоские структуры с той же симметрией, что и показанная, на самом деле имеют аналогичные структуры поляризации в импульсном пространстве 33,34,35,36 , и, таким образом, все они могут быть применены для реализации подобных сдвигов луча. Положение и направленность мод с круговой поляризацией соответствуют смоделированной карте поляризации. Принимая во внимание фактические спектры, показанные на рис. 3а, мы выбираем целевую длину волны 816 нм.Кроме того, мы экспериментально измерили фазовые распределения в кросс-поляризованном импульсном пространстве после взаимодействия с пластиной PhC, как показано на рис. 3b, с помощью нашей системы измерения фаз 39 . Измеренные фазовые распределения хорошо согласуются с нашими результатами моделирования и показывают ожидаемые результирующие фазовые градиенты в направлении k x .
Положение и направленность мод с круговой поляризацией соответствуют смоделированной карте поляризации. Принимая во внимание фактические спектры, показанные на рис. 3а, мы выбираем целевую длину волны 816 нм.Кроме того, мы экспериментально измерили фазовые распределения в кросс-поляризованном импульсном пространстве после взаимодействия с пластиной PhC, как показано на рис. 3b, с помощью нашей системы измерения фаз 39 . Измеренные фазовые распределения хорошо согласуются с нашими результатами моделирования и показывают ожидаемые результирующие фазовые градиенты в направлении k x . Мода с собственным состоянием поляризации LCP (RCP), отмеченная синей (красной) стрелкой, не будет реагировать на возбуждение RCP (LCP) и окажется уменьшенной точкой среди полосовых сигналов. b Измеренные фазовые распределения, вызванные кросс-поляризованным преобразованием пластины PhC на длине волны 816 нм. Падающая и анализируемая поляризации на левой (правой) панели равны \(\left|+45\right\rangle\) (\(\left|-45\right\rangle\)) и \(\left\langle — 45\вправо|\) (\(\влево\лангл +45\вправо|\)) соответственно. c Фазовые распределения вдоль линий, отмеченных b . Сплошные (штриховые) кривые на левой и правой панелях показывают фазовые распределения вдоль сплошных (штриховых) линий на левой и правой панелях b соответственно.
Мода с собственным состоянием поляризации LCP (RCP), отмеченная синей (красной) стрелкой, не будет реагировать на возбуждение RCP (LCP) и окажется уменьшенной точкой среди полосовых сигналов. b Измеренные фазовые распределения, вызванные кросс-поляризованным преобразованием пластины PhC на длине волны 816 нм. Падающая и анализируемая поляризации на левой (правой) панели равны \(\left|+45\right\rangle\) (\(\left|-45\right\rangle\)) и \(\left\langle — 45\вправо|\) (\(\влево\лангл +45\вправо|\)) соответственно. c Фазовые распределения вдоль линий, отмеченных b . Сплошные (штриховые) кривые на левой и правой панелях показывают фазовые распределения вдоль сплошных (штриховых) линий на левой и правой панелях b соответственно. Поляризация поляризатора падения и анализатора настроена на \(\left|+45\right\rangle\) и \(\left\langle -45\right|\), соответственно (\(\left|-45 \right\rangle\) и \(\left\langle +45\right|\) для другого случая). В последующих измерениях они не будут вращаться, чтобы избежать искусственных ошибок. Гауссовский световой пучок с длиной волны 816 нм от перестраиваемого лазера затем фокусируется на плоскости образца при нормальном падении, проходя через диафрагму на передней плоскости Фурье фокусирующей линзы, чтобы ограничить распределение луча k ∥ (расхождение угол).Радиус перетяжки луча (определяемый положением, в котором интенсивность 1/ e 2 максимальна) составляет около 4,1 мкм. После анализа анализатором распределение интенсивности исходящего луча фиксируется устройством с зарядовой связью (ПЗС), что позволяет нам непосредственно наблюдать за лучом.
Поляризация поляризатора падения и анализатора настроена на \(\left|+45\right\rangle\) и \(\left\langle -45\right|\), соответственно (\(\left|-45 \right\rangle\) и \(\left\langle +45\right|\) для другого случая). В последующих измерениях они не будут вращаться, чтобы избежать искусственных ошибок. Гауссовский световой пучок с длиной волны 816 нм от перестраиваемого лазера затем фокусируется на плоскости образца при нормальном падении, проходя через диафрагму на передней плоскости Фурье фокусирующей линзы, чтобы ограничить распределение луча k ∥ (расхождение угол).Радиус перетяжки луча (определяемый положением, в котором интенсивность 1/ e 2 максимальна) составляет около 4,1 мкм. После анализа анализатором распределение интенсивности исходящего луча фиксируется устройством с зарядовой связью (ПЗС), что позволяет нам непосредственно наблюдать за лучом. Несмотря на ортогональность поляризатора и анализатора, ограниченный коэффициент ослабления поляризаторов позволяет передавать очень небольшую часть луча без кросс-поляризованного преобразования.Таким образом, мы можем найти исходный луч и установить нули координат. На рисунке 4а показано нормализованное распределение интенсивности исходного прошедшего светового луча. Впоследствии мы переключаем образец на изготовленную плиту PhC. Как показано на рис. 4b, измеряется нормализованная интенсивность кросс-поляризованного луча. Поперечные сдвиги луча можно наблюдать непосредственно. Направления смещения луча согласуются с нашими теоретическими предсказаниями. На рис. 4в представлены распределения интенсивности вдоль линий, отмеченных на рис.4а, б, из которых мы можем сказать, что сдвиг пика интенсивности составляет около 4,2 мкм, что согласуется с оценочным сдвигом (около 4,3 мкм) от среднего фазового градиента, рассчитанного по измеренным фазовым картам (рис. 3б). Сдвиги четко наблюдаются, подтверждая наше предположение.
Несмотря на ортогональность поляризатора и анализатора, ограниченный коэффициент ослабления поляризаторов позволяет передавать очень небольшую часть луча без кросс-поляризованного преобразования.Таким образом, мы можем найти исходный луч и установить нули координат. На рисунке 4а показано нормализованное распределение интенсивности исходного прошедшего светового луча. Впоследствии мы переключаем образец на изготовленную плиту PhC. Как показано на рис. 4b, измеряется нормализованная интенсивность кросс-поляризованного луча. Поперечные сдвиги луча можно наблюдать непосредственно. Направления смещения луча согласуются с нашими теоретическими предсказаниями. На рис. 4в представлены распределения интенсивности вдоль линий, отмеченных на рис.4а, б, из которых мы можем сказать, что сдвиг пика интенсивности составляет около 4,2 мкм, что согласуется с оценочным сдвигом (около 4,3 мкм) от среднего фазового градиента, рассчитанного по измеренным фазовым картам (рис. 3б). Сдвиги четко наблюдаются, подтверждая наше предположение. Обратите внимание, что общий сдвиг луча без анализатора будет менее очевидным, так как в эксперименте только 12% падающей мощности преобразуется в проходящий кросс-поляризованный пучок. Результаты без анализа включены в дополнительное примечание 9.Мы также включаем другие результаты на разных длинах волн в Дополнительное примечание 10.
Обратите внимание, что общий сдвиг луча без анализатора будет менее очевидным, так как в эксперименте только 12% падающей мощности преобразуется в проходящий кросс-поляризованный пучок. Результаты без анализа включены в дополнительное примечание 9.Мы также включаем другие результаты на разных длинах волн в Дополнительное примечание 10. c Нормализованные распределения интенсивности наблюдаемых лучей вдоль оси x , срезы a и b . Пунктирные зеленые кривые соответствуют исходным лучам, показанным в a , тогда как сплошные оранжевые кривые соответствуют смещенным лучам, показанным в b , соответственно.Двунаправленная стрелка отмечает лучевую талию.
c Нормализованные распределения интенсивности наблюдаемых лучей вдоль оси x , срезы a и b . Пунктирные зеленые кривые соответствуют исходным лучам, показанным в a , тогда как сплошные оранжевые кривые соответствуют смещенным лучам, показанным в b , соответственно.Двунаправленная стрелка отмечает лучевую талию.
 ..
..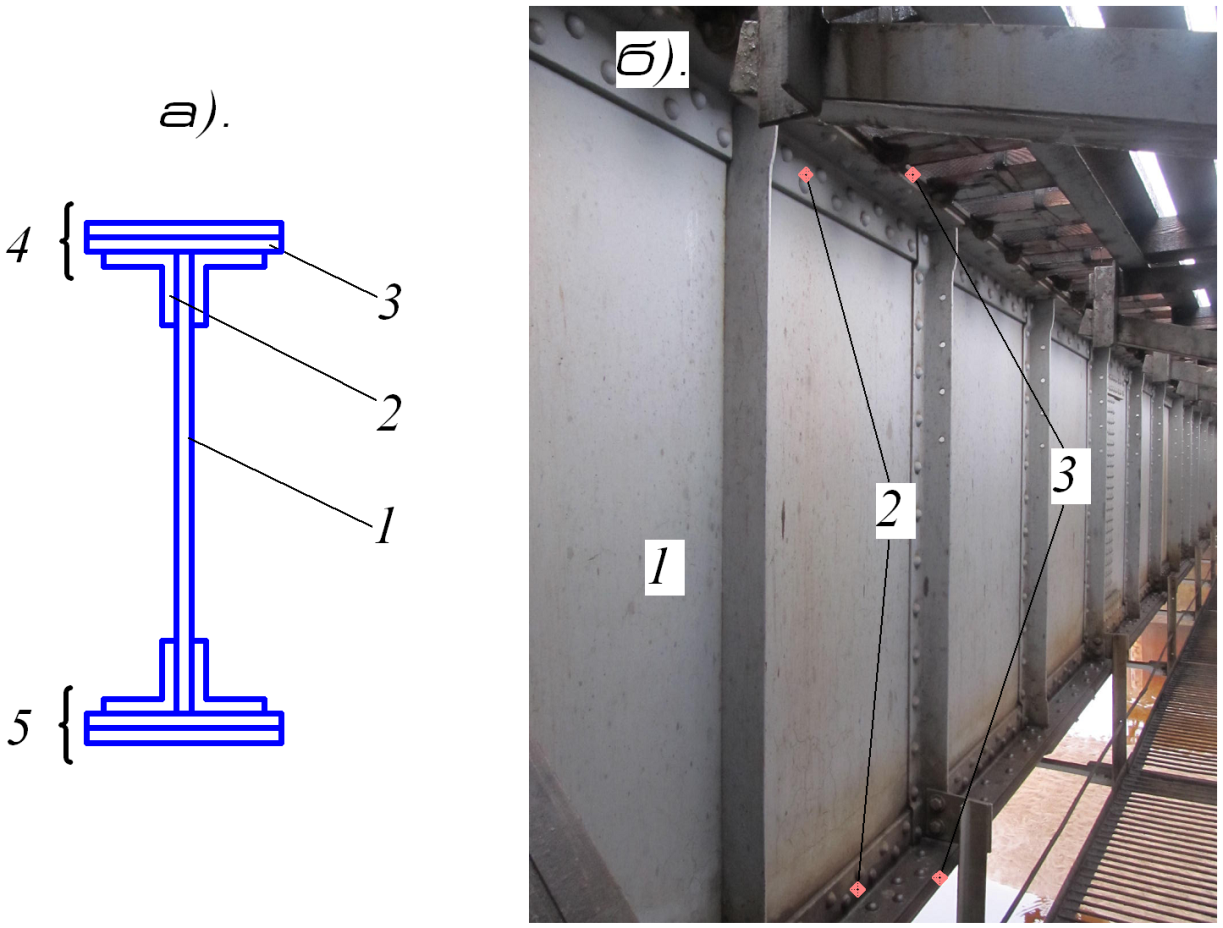 В последние одно-два десятилетия еще одной областью, которой уделяется значительное внимание, являются технологии космических двигателей, использующие ионные пучки от плазменных источников. Были разработаны различные плазменные двигатели для движения электрических космических аппаратов с целью уменьшить полезную нагрузку ракеты за счет отказа от использования твердого и жидкого топлива и с целью облегчения футуристических межпланетных путешествий на большие расстояния. Есть несколько других новых областей, в которых ионные пучки из плазмы играют решающую роль в расширении границ исследований.Одной из таких областей является нано-микроструктурирование на основе сфокусированного ионного пучка (FIB). Обычные системы FIB на основе жидких металлов полагаются на галлий в качестве источника ионов, который представляет собой жидкий металл при комнатной температуре. Источники FIB на основе Ga страдают от проблем с поверхностным загрязнением. Кроме того, из-за меньших токов им требуется огромное время измельчения даже для измельчения небольшого объема.
В последние одно-два десятилетия еще одной областью, которой уделяется значительное внимание, являются технологии космических двигателей, использующие ионные пучки от плазменных источников. Были разработаны различные плазменные двигатели для движения электрических космических аппаратов с целью уменьшить полезную нагрузку ракеты за счет отказа от использования твердого и жидкого топлива и с целью облегчения футуристических межпланетных путешествий на большие расстояния. Есть несколько других новых областей, в которых ионные пучки из плазмы играют решающую роль в расширении границ исследований.Одной из таких областей является нано-микроструктурирование на основе сфокусированного ионного пучка (FIB). Обычные системы FIB на основе жидких металлов полагаются на галлий в качестве источника ионов, который представляет собой жидкий металл при комнатной температуре. Источники FIB на основе Ga страдают от проблем с поверхностным загрязнением. Кроме того, из-за меньших токов им требуется огромное время измельчения даже для измельчения небольшого объема. Чтобы удовлетворить возникающие области исследований, такие как обработка биоматериалов и микрофлюидные приложения, где в промышленности требуется высокая пропускная способность, предпринимаются усилия по разработке источников сфокусированного ионного пучка из газообразной плазмы инертных газов, которые могут быть неэффективными. -токсичен, поэтому подходит для биоматериалов.Кроме того, они обеспечат возможность быстрой обработки за счет более высоких токов без металлического загрязнения. В последние годы еще одной целевой областью, в которой наблюдается широкая активность, являются низкоэнергетические ионные пучки на основе плазмы для модификации поверхности материалов и добавления к ним большей функциональности. Ионные пучки низкой энергии применялись для создания атомарно-гетерогенных систем, в которых ионы входят в решетку-хозяин и ограничиваются несколькими подповерхностными слоями, тем самым создавая неоднородность на атомном уровне.Они изменяют поверхность (смачиваемость), электрические и оптические свойства материалов.
Чтобы удовлетворить возникающие области исследований, такие как обработка биоматериалов и микрофлюидные приложения, где в промышленности требуется высокая пропускная способность, предпринимаются усилия по разработке источников сфокусированного ионного пучка из газообразной плазмы инертных газов, которые могут быть неэффективными. -токсичен, поэтому подходит для биоматериалов.Кроме того, они обеспечат возможность быстрой обработки за счет более высоких токов без металлического загрязнения. В последние годы еще одной целевой областью, в которой наблюдается широкая активность, являются низкоэнергетические ионные пучки на основе плазмы для модификации поверхности материалов и добавления к ним большей функциональности. Ионные пучки низкой энергии применялись для создания атомарно-гетерогенных систем, в которых ионы входят в решетку-хозяин и ограничиваются несколькими подповерхностными слоями, тем самым создавая неоднородность на атомном уровне.Они изменяют поверхность (смачиваемость), электрические и оптические свойства материалов. Было обнаружено, что от локализованной подповерхностной имплантации в микронном масштабе до облучения большой площади ливневыми ионными пучками, изменяя плотность потока пучка и ионные частицы, можно реализовать широко настраиваемые свойства материала.
Было обнаружено, что от локализованной подповерхностной имплантации в микронном масштабе до облучения большой площади ливневыми ионными пучками, изменяя плотность потока пучка и ионные частицы, можно реализовать широко настраиваемые свойства материала. Frontiers оставляет за собой право направить рукопись, выходящую за рамки рассмотрения, в более подходящий раздел или журнал на любом этапе рецензирования.
Frontiers оставляет за собой право направить рукопись, выходящую за рамки рассмотрения, в более подходящий раздел или журнал на любом этапе рецензирования.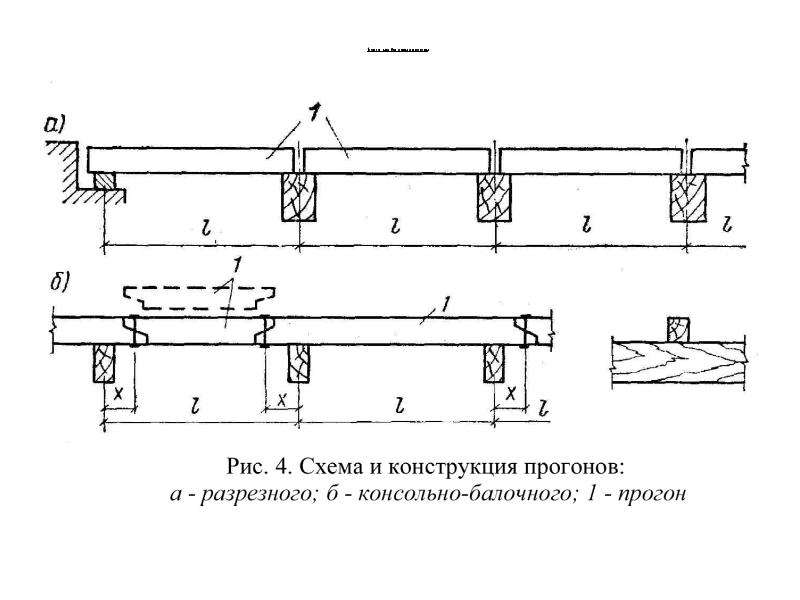 Это всегда дополнительное счастье, когда я снова в своей стране!»
Это всегда дополнительное счастье, когда я снова в своей стране!»


 (Общая физика) узкий однонаправленный поток электромагнитного излучения или частиц: пучок света; электронный пучок.
(Общая физика) узкий однонаправленный поток электромагнитного излучения или частиц: пучок света; электронный пучок. д.) с одного карманного компьютера на другой с помощью инфракрасных лучей
д.) с одного карманного компьютера на другой с помощью инфракрасных лучей
 д.)) для заранее определенной аудитории.
д.)) для заранее определенной аудитории. Однако этот уровень изящества и чутья не дается легко; это требует таланта, постоянной практики и многих тяжелых падений.
Однако этот уровень изящества и чутья не дается легко; это требует таланта, постоянной практики и многих тяжелых падений.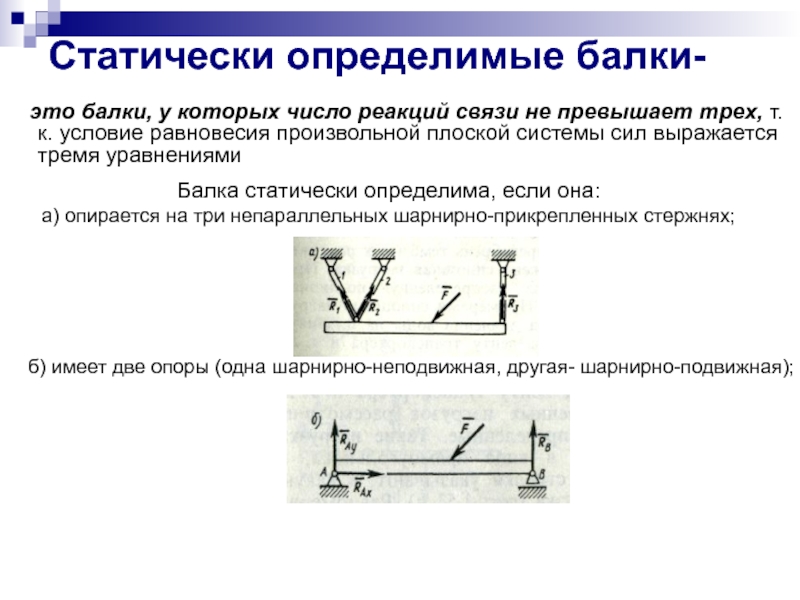 Вы должны учитывать некоторые ключевые факторы, чтобы получить наилучшее впечатление от гимнастики. Они могут спасти вас от травм или вреда, поэтому давайте обсудим их ниже.
Вы должны учитывать некоторые ключевые факторы, чтобы получить наилучшее впечатление от гимнастики. Они могут спасти вас от травм или вреда, поэтому давайте обсудим их ниже.
 Они далеко от земли (до 4,1 метра), что делает их сложными, но интригующими для исполнения.
Они далеко от земли (до 4,1 метра), что делает их сложными, но интригующими для исполнения.
 Блаженство. Складные бревна всегда лучше, потому что вы можете легко упаковать их в чехол для хранения и взять с собой в спортзал или на отдых или в поход. Некоторые жесткие балансиры также мобильны, но их сложно упаковать, транспортировать и установить.
Блаженство. Складные бревна всегда лучше, потому что вы можете легко упаковать их в чехол для хранения и взять с собой в спортзал или на отдых или в поход. Некоторые жесткие балансиры также мобильны, но их сложно упаковать, транспортировать и установить. Для специально разработанных подъемных балок и траверс-распорок это будет различаться в зависимости от типа балки, но, поскольку мы разрабатываем и производим сами, мы часто можем предложить быстрые сроки поставки и для траверс специальной конструкции.
Для специально разработанных подъемных балок и траверс-распорок это будет различаться в зависимости от типа балки, но, поскольку мы разрабатываем и производим сами, мы часто можем предложить быстрые сроки поставки и для траверс специальной конструкции.