Динамическая нагрузка: «Чем динамическая нагрузка отличается от статической?» – Яндекс.Кью
- Вагоны нагрузка динамическая, статическая — Энциклопедия по машиностроению XXL
- Нагрузка вагона динамическая — Справочник химика 21
- Статическая или динамическая нагрузка?
- Физические нагрузки, активный образ жизни
- Расчет на ударные нагрузки — Доктор Лом
- Теоретические предпосылки расчета
- Теория расчета на динамическую нагрузку
- Теория расчета на ударную нагрузку
- Пример расчета балки на ударную нагрузку
- Пример расчета балки на ударную нагрузку от груза, падающего не посредине балки
- Пример расчета балки на ударную нагрузку с учетом жесткости падающего груза
- 2.Расчет и выбор подшипников
- Эквивалентная динамическая нагрузка | Арболит
- Статическая нагрузка против. Динамическая нагрузка: Демистификация грузоподъемности поддонов
- Отклонение статической и динамической нагрузки
- В чем разница между статическими и динамическими нагрузками?
- Произошла ошибка при настройке пользовательского файла cookie
- Расчетные коэффициенты для динамических нагрузок
- Реализовать трехфазную динамическую нагрузку с активной мощностью и реактивная мощность как функция напряжения или управляемая от внешнего вход
- Динамическая нагрузка на исходном уровне может предсказать рентгенографическое прогрессирование заболевания при остеоартрите медиального отдела коленного сустава
Вагоны нагрузка динамическая, статическая — Энциклопедия по машиностроению XXL
На вагон действуют а) статические нагрузки (постоянные силы) (см. табл. 5) и б) динамические нагрузки (переменные силы) (см. табл. 6). Расчёт выполняется в двух вариантах 1) с учётом только одних статических нагрузок и 2) с учётом совместного действия статических и динамических нагрузок при наиболее неблагоприятном их сочетании.
[c.637]
По характеру действия нагрузки делятся на статические и динамические. Статические нагрузки прикладываются к конструкциям постепенно и остаются почти неизменными в течение всего времени работы конструкции. Динамические нагрузки действуют непродолжительное время и достигают значительных величин в малый отрезок времени. Их возникновение в большинстве случаев связано с силами инерции. Например, шатун и ползун быстроходного кривошипно-ползунного механизма во время работы получают большие динамические нагрузки от изменения величины и направления скоростей. Значительные динамические нагрузки создаются также на сцепки вагонов при трогании состава с места, на детали пневматических молотков и других машин ударного действия.
[c.156]
Значительные динамические нагрузки создаются также на сцепки вагонов при трогании состава с места, на детали пневматических молотков и других машин ударного действия.
[c.156]
Для повышения динамической нагрузки необходимо вагоны, имеющие большую статическую нагрузку, отправлять на более дальние расстояния, чем вагоны с меньшей статической нагрузкой.
[c.36]
Использование грузоподъемности вагона характеризуется его статической и динамической нагрузками. Динамическая нагрузка — это средняя нагрузка вагона с учетом пробега в груженом состоянии [c.236]
Когда вагон неподвижен, пружины подвески испытывают только статическую нагрузку от массы кузова. При движении по неровностям пути кузов совершает вертикальные колебания, поэтому нагрузка на пружины существенно изменяется. Величину, на которую она увеличивается или уменьшается, называют динамической нагрузкой. Суммируя статическую и динамическую нагрузки, рассчитывают прочность пружин, по разности этих нагрузок определяют минимальное давление колесной пары на путь, чтобы исключить возможность схода с рельсов, т.е. обеспечить безопасное качение колесной пары.
[c.64]
Суммируя статическую и динамическую нагрузки, рассчитывают прочность пружин, по разности этих нагрузок определяют минимальное давление колесной пары на путь, чтобы исключить возможность схода с рельсов, т.е. обеспечить безопасное качение колесной пары.
[c.64]
Нагрузка на рельсы складывается из статической (вес кузова и тележки) и динамической (силы инерции кузова). Давление вагона на рельсы найдем из условия равновесия всех сил (включая и силу инерции), действующих па вагон [c.408]
При расчёте оси на основные силы исходят из действующих сил а) максимальной статической нагрузки на одну шейку Q б) динамической нагрузки Сц, приходящейся на одну колёсную пару от центробежной силы в) то же от силы ветра С в , г) инерционного усилия /при торможении. Кроме того, учитывается динамическая надбавка от действия стыков рельсов на ось (на неподрессоренную часть вагона). Схема нагрузки дана на фиг. 96. [c.698]
Основными качественными показателями использования вагонов являются по грузовому парку — статическая и динамическая нагрузки, оборот вагона, время нахождения вагона в неисправном состоянии, груженый и полный рейс, среднесуточный пробег и производительность вагона по пассажирскому парку — оборот пассажирского состава, среднесуточный пробег и средняя населенность вагона на ось. [c.14]
[c.14]
Показателями, характеризующими нагрузку вагона и степень использования его грузоподъемности, являются статическая и динамическая нагрузки. [c.15]
Чем выше статическая и динамическая нагрузки, тем меньше вагонов потребуется для выполнения плана перевозок, следовательно, тем ниже себестоимость перевозок. [c.16]
Качественные показатели характеризуют использование локомотивов и вагонов. К ним относят оборот, среднесуточные пробеги и производительность локомотива, оборот и среднесуточный пробег вагона, использование подъемной силы вагона, статическую, динамическую нагрузку и производительность грузового вагона. [c.30]
Пассажирские дороги испытывают с участием представителя инспекции Госгортехнадзора. Вагоны дорог с маятниковым движением испытывают на двойную статическую нагрузку в течение 30 мин и затем на динамическую, равную 1,25 расчетной. Испытания проводят последовательным, а затем одновременным включением рабочего и аварийного тормозов при работающей дороге. Кабины одноканатных дорог с кольцевым движением испытывают только на статическую нагрузку двойным грузом в течение 15 мин. Кроме тщательного освидетельствования механического и электрического оборудования, при испытаниях проверяют работу ловителей вагонов.
[c.240]
Испытания проводят последовательным, а затем одновременным включением рабочего и аварийного тормозов при работающей дороге. Кабины одноканатных дорог с кольцевым движением испытывают только на статическую нагрузку двойным грузом в течение 15 мин. Кроме тщательного освидетельствования механического и электрического оборудования, при испытаниях проверяют работу ловителей вагонов.
[c.240]
Коэффициентом вертикальной динамики к, называется отношение дополнительной динамической нагрузки Р на элемент конструкции вагона к статической нагрузке Рст- [c.118]
Вертикальная нагрузка — слагающаяся из статически приложенных собственного веса, полезной нагрузки, обусловленной техническим заданием на проектирование и динамических сил, возникающих при движении вагона. Динамические силы определяют умножением статической нагрузки на коэффициент вертикальной динамики 0,00079 (а-15,3) [c.359]
Характерными представителями этого типа конструкций являются кузова цельнометаллических вагонов и корпуса судов. Общим для них является использование плоских или криволинейных полотнищ с последующим объединением их в жесткую пространственную конструкцию, способную воспринимать статические, вибрационные и динамические нагрузки.
[c.640]
Общим для них является использование плоских или криволинейных полотнищ с последующим объединением их в жесткую пространственную конструкцию, способную воспринимать статические, вибрационные и динамические нагрузки.
[c.640]
Масса предъявляемого к перевозке в крытых вагонах и контейнерах пакета цветных металлов при ширине его 770 вш не должна превышать 1500 кг при ширине 820 им — 1450 кг при ширине 100 мы — 1400 кг при ширине 1100 ын — 1350 кг. Статическая нагрузка, действующая на пол вагона от колеса погрузчика с грузом, не должна превышать 18 кН, а динамическая нагрузка — 22 кН. [c.92]
На колёсную пару при движении действуют вертикальные и горизонтальные статические и динамические нагрузки, которые могут быть сведены к двум вертикальным силам Рг и Рз> прижимающим колёса к рельсам, и одной горизонтальной (действующей на колёсную пару вдоль её оси от рамы вагона или рамы тележки — рамное усилие) силе. Р, стремящейся сдвинуть колёсную пару поперёк пути (фиг. 32).
[c.682]
32).
[c.682]
Несущие рамы применяются при кузовах капотного, а также вагонного (закрытого) типов и воспринимают основные статические и динамические нагрузки. При несущих рамах кузова выполняют легко съемными, что существенно улучшает условия сборки и ремонта тепловозов. [c.139]
Динамическую нагрузку в поездном режиме определяют, умножая собственный вес и полезную нагрузку (нагрузку брутто) на коэффициент вертикальной динамики. Расчетный коэффициент вертикальной динамики определяют в зависимости от скорости движения V (в км/ч) и статического прогиба (в см) рессорного подвешивания вагона-самосвала под нагрузкой брутто по следующим формулам [c.168]
Степень использования грузоподъемности вагонов характеризуется его нагрузкой. Различают два вида нагрузок, а именно нагрузку статическую и нагрузку динамическую. Статическая нагрузка является показателем, характеризующим качество использования грузоподъеме10сти вагонов при его погрузке, и выражается числом тонн груза, приходящегося в среднем на один вагон. Динамическая нагрузка в отличие от статической характеризует степень использования грузоподъемности вагона с учетом расстояния пробега вагона и определяется как частное от деления выполненных тонно-километров на вагоно-километры пробега и выражается количеством тонн груза, приходящегося на вагон на всем пути следования.
[c.350]
Динамическая нагрузка в отличие от статической характеризует степень использования грузоподъемности вагона с учетом расстояния пробега вагона и определяется как частное от деления выполненных тонно-километров на вагоно-километры пробега и выражается количеством тонн груза, приходящегося на вагон на всем пути следования.
[c.350]
Использование грузоподъемности вагона характеризуется его статической. (см. п. 27.2) и. динамической нагрузкам (. Дин ическая нагрузка — это средняя н1агрузка вагона с учетом расстояния пробегов груженом состоянии [c.261]
Качество выполняемой железными дорогами эксплуагационной работы по перевозке грузов и эффективность использования при этом подвижного состава определяются следующими основными показателями оборот вагона и локомотива, среднесуточный пробег вагона и локомотива, статическая и динамическая нагрузки вагона, производительность вагона и локомотива, техническая и участковая скорости движения поездов.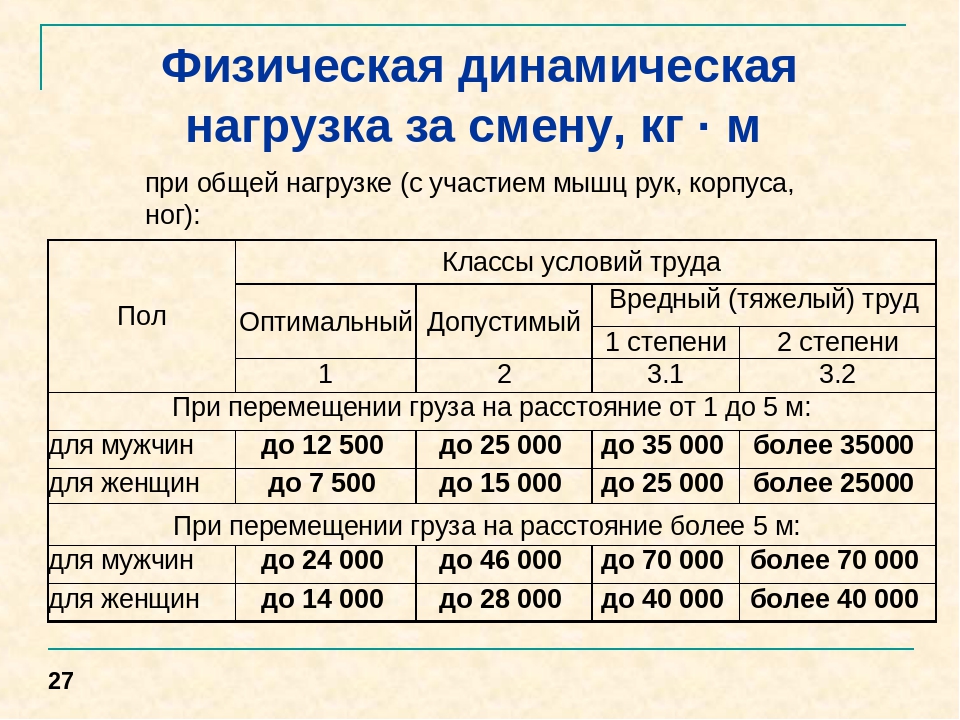 [c.349]
[c.349]
Когда вагон неподвижен, пружины подвески испытывают т олько статическую нагрузку от массы кузова. При движении по неровностям пути кузов совершает вертикальные колебания, поэтому нагрузка на пружины существенно изменяется. Величину, на которую она увеличивается или уменьшается, называют динамической нагрузкой. Суммируя статическую и динамическую нагрузки, рассчитывают прочносп. пружин, по разности этих нагрузок оп-
[c.100]
На прицепных и моторных вагонах электропоездов Э1 9М и ЭР9Е применено двойное рессорное подвешивание (рис. 7), состоящее из двух ступеней — буксового подвешивания и центрального, работающих последовательно. В отличие от электропоездов ЭР9 в конструкциях рессорного подвешивания электропоездов ЭР9М и ЭР9Е применены только цилиндрические пружины. Их изготовляют из стального прутка, который навивается на цилиндр диаметром, равным внутреннему размеру пружины. Для придания пружине необходимой упругости ее подвергают закалке. Применение цилиндрических пружин вместо листовых рессор обусловлено тем, что листовые рессоры имеют значительное внутреннее трение между листами, поэтому при движении электропоезда возникают высокочастотные колебания. Эти колебания в зависимости от частоты воспринимаются пассажирами в виде дрожания, шума или качки. Применение цилиндрических пружин, не обладающих внутренним трением, обеспечивает вагону плавный и бесшумный ход. У неподвижного вагона пружины испытывают только статическую нагрузку. При движении вагона по неровностям пути его кузов совершает вертикальное колебательное движение. При этом в некоторые моменты времени нагрузка на пружины или увеличивается или уменьшается по сравнению со статической на величину, называемую динамической нагрузкой. Наибольшая нагрузка на пружину, т. е. сумма статической и динамической нагрузок, служит для расчета пружин на прочность. По наименьшей нагрузке — разности статической и динамической нагрузок — судят о минимальном давлении колесной пары на рельс и о безопасности движения колесных пар (возможности схода с рельсов).
Для придания пружине необходимой упругости ее подвергают закалке. Применение цилиндрических пружин вместо листовых рессор обусловлено тем, что листовые рессоры имеют значительное внутреннее трение между листами, поэтому при движении электропоезда возникают высокочастотные колебания. Эти колебания в зависимости от частоты воспринимаются пассажирами в виде дрожания, шума или качки. Применение цилиндрических пружин, не обладающих внутренним трением, обеспечивает вагону плавный и бесшумный ход. У неподвижного вагона пружины испытывают только статическую нагрузку. При движении вагона по неровностям пути его кузов совершает вертикальное колебательное движение. При этом в некоторые моменты времени нагрузка на пружины или увеличивается или уменьшается по сравнению со статической на величину, называемую динамической нагрузкой. Наибольшая нагрузка на пружину, т. е. сумма статической и динамической нагрузок, служит для расчета пружин на прочность. По наименьшей нагрузке — разности статической и динамической нагрузок — судят о минимальном давлении колесной пары на рельс и о безопасности движения колесных пар (возможности схода с рельсов). [c.12]
[c.12]
Со второй половины 30-х годов сварка получает широкое применение в различных отраслях машиностроения при изготовлении различных деталей и узлов машин. В транспортном машиностроении в середине 30-х годов совершился широкий переход с клепки на сварку всех основных вагонных конструкций. В это дело много труда вложили С. 3. Штерлинг, Г. А. Николаев и др. Указанное мероприятие позволило резко увеличить выпуск вагонов и показало, что сварные изделия могут успешно эксплуатироваться не только при статических, но и при динамических нагрузках [213]. [c.117]
Вагонные детали из древесины и древесных материалов для вагонов всех видов (грузовых и пассажирских), включая вагоны метрополитена, согласно ГОСТ 3191—75 подразделяют по пазначсншо и качеству на три группы 1 — детали, работающие при повышенных динамических нагрузках, и детали, подвергающиеся нрозрачпоп отделке 2 — нагруженные, подвергающиеся динамическим пли значптолгл ым статическим нагрузкам п не подвергающиеся прозрачной отделке 3 — слабонагруженные детали и детали, имеющие вспомогательное значение в конструкции вагонов. [c.350]
[c.350]
Расчёт вагонных осей [3]. На колёсную пару действует статическая нагрузка от веса вагона (за вычетом веса колёс) и веса груза, а также динамические усилия 1) вертикальные— от ударов о рельсы на стрелках, сты ках и т. д. 2) горизонтальные — от ударов реборды колеса при. прохождении кривых 3) вертикальные составляющие от центробежной силы и силы ветра 4) силы инерции 5) скручивающие усилия при прохождении кривых 6) силы торможения 7) усилия от действия тяговых моторов (в тележках элек-тровагоиов). [c.698]
Общие положения. Внброизоляцию как принцип защиты оборудования, чувствительного к динамическим нагрузкам, широко применяют в различных областях 1ехники, При этом в одних случаях системы виброизоляции можно конструировать в комплексе с защищаемым объектом в качестве его неотъемлемой части (например, подвески железнодорожных вагонов и автомобилей, корабельных дизельных установок и т. п.) в других случаях, например при защите от вибрации радиоэлектронной аппаратуры, где одни и те же приборы и оборудование в зависимости от мест установки подвергаются совершенно различным по форме или интенсивности возбуждениям, проектирование виброзащитных систем носит индивидуальный характер и выполняют его по результатам статического и динамического расчетов. [c.188]
[c.188]
Степень использования грузоподъемности вагона характеризуется статической и динамической нагрузками. Статическая нагрузка на вагон или на ось есть отношение массы груза в вагонах к общему числу загруженных вагонов т/вагон) или к общему числу ваго1 ов-осей т1ось). [c.31]
Вагоны двухканатных ППКД с маятниковым движением испытываются статической нагрузкой, равной 200% расчетной, в течение 30 мин и динамической, равной 125% расчетной. [c.236]
Полная дополнитель] ая динамическая нагрузка от колёс одной стороны вагона на внешний рельс при действии боковых сил с учётом перераспределения статической нагрузки между колёсами от перемещения центра тяжести кузова, вызваниого деформациями рессор, равна (фиг. 34) [c.684]
Конструкция пола рассчитываемого вагона (полувагона с плоским полом, образуемым крышками люков) позволяет считать, что нагрузки Ql, Qj и Qj поровну распределяются между хребтовой балкой и боковыми стенками. Уравновеп1Иваются указанные нагрузки соо г-ветствующими реакциями пятников. Вертикальную динамическую нагрузку определяют в зависимости от статического прогиба рессорного подвешивания (см. стр. 714), и в данном случае она составляет 45% от нагрузки брутто. В расчёте эту нагрузку учитывают только при определении напряжений.
[c.751]
Уравновеп1Иваются указанные нагрузки соо г-ветствующими реакциями пятников. Вертикальную динамическую нагрузку определяют в зависимости от статического прогиба рессорного подвешивания (см. стр. 714), и в данном случае она составляет 45% от нагрузки брутто. В расчёте эту нагрузку учитывают только при определении напряжений.
[c.751]
По варианту 2 разработана конструкция, проведены ее испытания на стенде и в условиях эксплуатации с тепловозом ТЭМ7. Предусмотрена возможность перераспределения нагрузки (нагрузка девятой оси может быть уменьшена с 200 до 63 кН). Вагонная колесная пара является поддерживающей. Статический прогиб подвешивания этой колесной пары 150 мм, возможность поперечного перемещения в кривых +250 мм. Испытания тепловоза ТЭМ7 с такой тележкой показали, что при наличии девятой оси динамические качества, устойчивость движения и воздействие на путь девятиосного экипажа не ухудшились (по сравнению с восьмиосным). [c.20]
[c.20]
При проектировании вагонов особое внимание должно уделяться их динамическим воздействиям на железнодорожный путь. Дополнительные динамические вертикальные силы, передаваемые колесом вагона рельсу, вызванные колебаниями надрессорного строения, не должны превышать статическую нагрузку кузова на колесо. Если эти силы достигнут величин, равных статической нагрузке на колесо (8—10 г), то при колебаниях надрессорного строения будут возникать такие же силы разгрузки колеса, т. е. произойдет полное обез-груживание колеса. Это крайне опасно, поскольку обезгру-женное колесо может сойти с рельса (см. лекцию 8). [c.79]
Нагрузка вагона динамическая — Справочник химика 21
С помощью показателей второй группы оценивается степень исг пользования грузоподъемности вагонов и силы тяги локомотивов.. К ним относятся статическая нагрузка вагона (Г) динамическая нагрузка вагона (ткм/вагоно-км или ткм/осе-км) производительность вагона (ткм).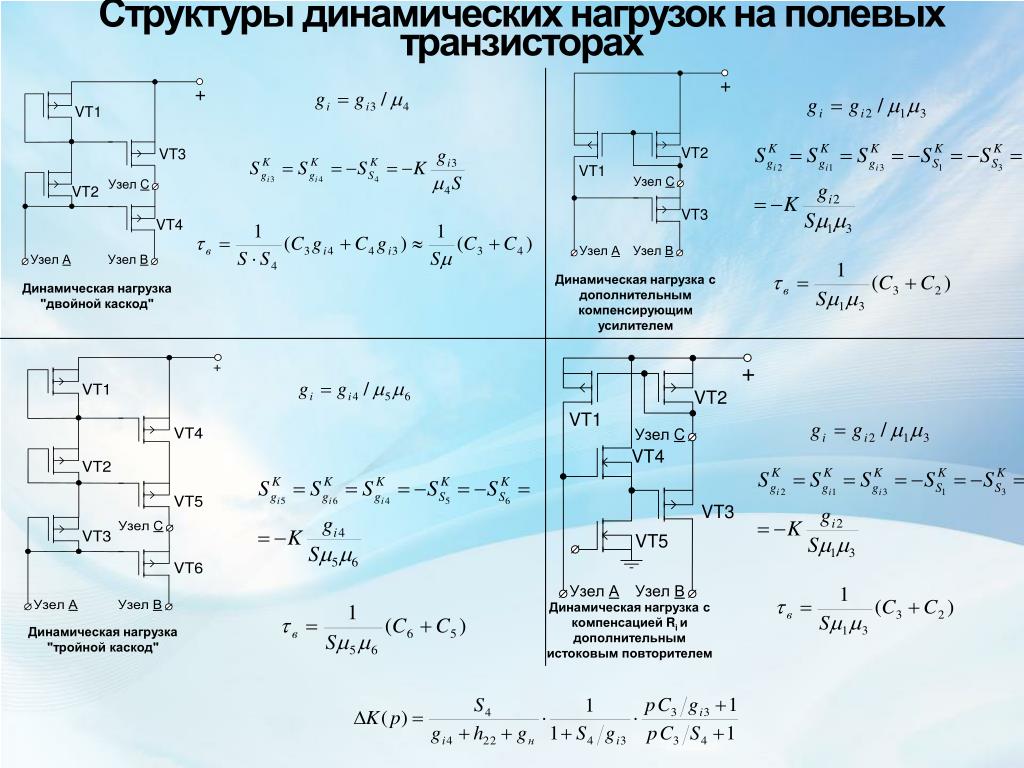 [c.208]
[c.208]
Динамические нагрузки, возникаюш,ие в процессе эксплуатации сосудов, усиливают давление материала на стенки. Учитывается это умножением расчетных напряжений на коэффициент динамичности /Сд, имеющий следующие значения для транспортных бункеров /Сд = 1,6 для сосудов с вибраторами /Сд = 1,5 при загрузке материалов с высоты из вагонов и автомобилей [c.19]
Рычажные весы, установленные на загрузочных вагонах, как и башенные весы, имеют недостатки сложная настройка, громоздкость, плохое противостояние динамическим нагрузкам. Поэтому при переездах загрузочного вагона весы должны быть заарретированы, чтобы избежать нарушения точности взвешивания. Периодически, не реже одного раза в месяц, весы должен проверять весовой мастер. [c.164]
Износ радиальной поверхности вкладыша недопустим, так как при отсутствии сферической поверхности он жестко всей площадью соприкасается с верхней частью корпуса буксы и при динамических нагрузках вызывает преждевременный выход подшипников из строя, часто приводит к поломке пружин в рессорных комплектах тележек. Поэтому при ремонте вагонов все вкладыши обязательно промывают, осматривают и обмеряют. Длина вкладыша для осей типа III должна быть в пределах 246—249,5 мм, толщина средней части — от 22,5 до 26,5 МхМ. Неперпендикулярность торцовых поверхностей к оси вкладыша допускается не более 1 мм. Отремонтированные вкладыши должны иметь толщину средней части 25 о. 1 мм. В буксы одной колесной пары вкладыши должны ставиться с разницей по толщине в средней части не свыше 2 мм. При заводском и деповском ремонтах вагонов, если износ спинки вкладыша более 2 мм, радиальную поверхность его должны восстанавливать таким образом, чтобы радиус был 1500 мм. [c.18]
Поэтому при ремонте вагонов все вкладыши обязательно промывают, осматривают и обмеряют. Длина вкладыша для осей типа III должна быть в пределах 246—249,5 мм, толщина средней части — от 22,5 до 26,5 МхМ. Неперпендикулярность торцовых поверхностей к оси вкладыша допускается не более 1 мм. Отремонтированные вкладыши должны иметь толщину средней части 25 о. 1 мм. В буксы одной колесной пары вкладыши должны ставиться с разницей по толщине в средней части не свыше 2 мм. При заводском и деповском ремонтах вагонов, если износ спинки вкладыша более 2 мм, радиальную поверхность его должны восстанавливать таким образом, чтобы радиус был 1500 мм. [c.18]
При проезде автомобиля (вагонетки, вагона) через весы возникают динамические нагрузки, а поэтому расчетные нагрузки берут с коэффициентом динамичности д=1,1—1,2. [c.30]
Качественные — позволяют оценить затраты технических средств транспорта на выполнение перевозочной работы и главным образом степень использования подвижного состава и выполнение графика движения поездов. К этой группе относятся показатели использования вагонов грузового и пассажирского парка —время оборота грузового вагона и пассажирского состава, участковая скорость движения, среднесуточный пробег и населенность пассажирских вагонов, среднесуточный пробег, статическая и динамическая нагрузка грузового вагона, производительность грузового вагона, время простоя вагонов под грузовыми операциями и на технических станциях [c.9]
К этой группе относятся показатели использования вагонов грузового и пассажирского парка —время оборота грузового вагона и пассажирского состава, участковая скорость движения, среднесуточный пробег и населенность пассажирских вагонов, среднесуточный пробег, статическая и динамическая нагрузка грузового вагона, производительность грузового вагона, время простоя вагонов под грузовыми операциями и на технических станциях [c.9]
Пример. Определить изменение себестоимости перевозок на дороге при повышении на 10% динамической нагрузки на ось гружёного вагона при следующих исходных условиях [c.324]
Динамическая нагрузка на ось гружёного вагона р = 1 О т. [c.324]
Динамическая нагрузка рабочего вагона характеризует степень использования подъёмной силы вагонов рабочего парка с учётом расстояния пробега вагонов и определяется по формуле [c.355]
Подсчёт динамической нагрузки может быть произведён как в целом для всех вагонов рабочего парка (включая и порожние), так и в отношении гружёных вагонов (без порожних). [c.355]
[c.355]
Динамическую нагрузку гружёного вагона можно найти по формулам [c.355]
Статическая и динамическая нагрузка оказывает большое влияние на экономические результаты работы транспорта. Поэтому необходимо стремиться к всемерному повышению загрузки вагонов и в особенности динамической нагрузки за счёт применения передовых методов уплотнённой погрузки и сокращения порожнего пробега вагонов. [c.355]
Чем больше пробег полногрузных вагонов и чем меньше пробег легковесных и порожних вагонов, тем выше динамическая нагрузка вагона. [c.355]
Квартальные и годовые отчёты, наряду с выполнением плана перевозок в вагонах, норм оборота вагона и локомотива и их элементов, отражают также выполнение квартальных и годовых планов перевозок в тоннах, заданий по пробегу подвижного состава (локо-мотиво-километры, поездо-километры, вагоно-осе-километры) и некоторых показателей использования подвижного состава, имеющихся только в месячной статистической отчётности (так называемой тяжёлой отчётности). К этим показателям относят вес и состав поезда, динамическую и статическую нагрузки вагона, процент вспомогательного пробега локомотивов. [c.397]
К этим показателям относят вес и состав поезда, динамическую и статическую нагрузки вагона, процент вспомогательного пробега локомотивов. [c.397]
Использование грузонодъемности вагона характеризуется статической и динамической нагрузкой. Статическая нагрузка — это среднее количество тонн, приходящихся на вагон (ось вагона) при [c.19]
Массы древесные прессовочные применяются в качестве конструкционных материалов для изготовления средненагруженных деталей, выдерживающих динамические и статические нагрузки (корпуса подшипников, стаканы конвейеров, подставки под аккумуляторы пассажирских и багажных вагонов, втулки кронштейнов, подвески башмаков вагонов и т. п.), деталей антифрикционного назначения (сколь-зуны электропоездов, работаю1цие при 60 °С при различной влажности воздуха и в абразивной среде, вкладыши подшипников в машинах горнорудной, металлургической и легкой промышленности со сроком работы свыше 5 лет и т. п.), в качестве электроизоляционных материалов с повышенными физико-механическими показателями (корпус щеткодержателей электропоездов, обеспечивающий электроизоляцию при напряжении 3000 В и выдерживающий 15-10 циклов воздействия динамического усилия, создающего напряжение в детали 100 кгс/см при ускорении 20 и т. п.), а также в качестве теплоизоляционных материалов и материалов строительного и декоративного назначения (сиденья стульев вагонов, плинтусы, поручни, панели диванов, вагонные рамы пассажирских вагонов и т. п.). [c.60]
п.), а также в качестве теплоизоляционных материалов и материалов строительного и декоративного назначения (сиденья стульев вагонов, плинтусы, поручни, панели диванов, вагонные рамы пассажирских вагонов и т. п.). [c.60]
Произведённый таким образом расчёт показал, что с повышением динамической нагрузки на ось вагона на 10% себестоимость перевозок сокращается с 3,4006 коп1ткм до 3,2907 коп ткм. т. е. на. 3,2%. [c.324]
Статическая или динамическая нагрузка?
Люди бегают. Они считают, что бег единственный способ для достижения желаемого результата, как правило, снижения веса.
Да, это так. Но, опять же, не совсем. Динамичная нагрузка далеко не единственный способ держать себя в отличной физической форме. Бег – это движение, динамика, тело постоянно меняет свое положение, бег требует выносливости и силы. Для бега нужно пространство. Можно ли, выполняя статические упражнения, прокачать и нагрузить мышцы? Ответ: да!
Статическая нагрузка против динамической
К статике мы относим такое положение тела, при котором нельзя шевелиться, тело должно замереть в определенном положении. Яркий пример, упражнение планка. Данное упражнение является самым эффективным для тренировки мышц пресса, также спортсмены его любят за то, что одновременно с брюшной мышцей работают руки и спина. Выполняется упражнение следующим образом: принимаете позу планки, при этом тело должно быть идеально ровным. Поясничный прогиб при выполнении упражнения обязательно убирается. Напрягаются мышцы пресса, спины, рук. В таком положении необходимо провести минимум минуту. Натренированные люди выполняют его гораздо дольше. Вот она статика в чистом виде!
Яркий пример, упражнение планка. Данное упражнение является самым эффективным для тренировки мышц пресса, также спортсмены его любят за то, что одновременно с брюшной мышцей работают руки и спина. Выполняется упражнение следующим образом: принимаете позу планки, при этом тело должно быть идеально ровным. Поясничный прогиб при выполнении упражнения обязательно убирается. Напрягаются мышцы пресса, спины, рук. В таком положении необходимо провести минимум минуту. Натренированные люди выполняют его гораздо дольше. Вот она статика в чистом виде!
Статические упражнения отличный конкурент динамическим
Хатха йога – яркий пример статики. Нет ни бега, нет динамичных движений. Лишь ровное дыхание через нос, плавность в движении и фиксация поз. Выносливость приобретается и с йогой тоже. При чем невероятно эффективно, кто не уверен предлагаю попробовать. А, соответственно, и со статической нагрузкой.
Динамическая нагрузка представляет собой движение. Статическая нагрузка характеризуется спокойствием статуи. Динамика меняется, статика неподвластна движению. Не существует разницы между ними в качестве проработки той или иной части тела или группы мышц. Лишь место играет роль. Статическая нагрузка идеальна в замкнутых пространствах, в квартирах, спортивных залах. Динамическая нагрузка требует пространства, свободу движения. Упражнения со статической нагрузкой можно выполнять дома, для них не требуется много места. Возвращаясь к Хатха йоге, хочется добавить, что индийские йоги выделяются своей выносливостью, поражающими до онемения способностями, непоколебимым здоровьем.
Динамика меняется, статика неподвластна движению. Не существует разницы между ними в качестве проработки той или иной части тела или группы мышц. Лишь место играет роль. Статическая нагрузка идеальна в замкнутых пространствах, в квартирах, спортивных залах. Динамическая нагрузка требует пространства, свободу движения. Упражнения со статической нагрузкой можно выполнять дома, для них не требуется много места. Возвращаясь к Хатха йоге, хочется добавить, что индийские йоги выделяются своей выносливостью, поражающими до онемения способностями, непоколебимым здоровьем.
Вывод: статическая нагрузка ни чуть не уступает динамической. Некоторые статические упражнения даже наиболее эффективны. Используйте статическую нагрузку наряду с динамической и тогда тренировки будут эффективными, разнообразными, более экономичными по времени.
Физические нагрузки, активный образ жизни
доктора
Спорт как элемент здорового образа жизни
Здоровый образ жизни включает в себя ряд мероприятий, улучшающих здоровье и самочувствие. Одним из таковых является спорт, а точнее – физические нагрузки. Активность в течение дня играет огромную роль в профилактике многих заболеваний. И даже если у вас нет времени или же состояние вашего здоровья не позволяет заниматься спортом серьезно – вы всегда можете найти возможность поддерживать уровень физической активности, подходящий для вас.
Одним из таковых является спорт, а точнее – физические нагрузки. Активность в течение дня играет огромную роль в профилактике многих заболеваний. И даже если у вас нет времени или же состояние вашего здоровья не позволяет заниматься спортом серьезно – вы всегда можете найти возможность поддерживать уровень физической активности, подходящий для вас.
Динамические нагрузки
Полезнее всего для организма динамическая нагрузка – то есть движение. К этому типу физической активности относятся бег, плавание, пешая ходьба, а также такие популярные упражнения как выпады, приседания, скручивания.
Что дают регулярные динамические нагрузки?
- Проработанная программа упражнений помогает строить тело;
- Упражнения способствуют росту мышечной массы;
- Возрастает энергопотребление – причем не только в процессе нагрузки, но и в покое;
- Увеличивается объем легких и глубина дыхания;
- Все ткани организма интенсивнее снабжаются кислородом;
- Улучшается обмен веществ;
- Снижается риск развития заболеваний опорно- двигательного аппарата.

Статические нагрузки
Нагрузка – это не обязательно движение. Длительное пребывание в одном положении тоже может быть для мышц нагрузкой. Если состояние здоровья не позволяет вам практиковать динамичные нагрузки, вы можете прибегать к статическим. Они не требуют активного движения, напротив – в процессе вы должны сохранять определенное положение или очень медленно менять его (как, например, в йоге или пилатесе). Такие нагрузки показаны даже при заболеваниях сердечно-сосудистой системы или опорно-двигательного аппарата, которые не позволяют заниматься динамической активностью.
Норма суточной активности
Не существует конкретного показателя активности, который можно было бы назвать универсальным. Кто-то устает, поднявшись на третий этаж, а кто-то может провести 2-3 часа в тренажерном зале и сохранить бодрость.
Выбирайте нагрузку по себе, прислушивайтесь к своему организму. В день нужно проходить минимум 3-5 км (это 5000-7000 шагов) – такой уровень нагрузки считается минимальным.
Как рассчитывать ЧСС для спорта
Аббревиатура ЧСС расшифровывается как «частота сердечных сокращений», иначе говоря, это пульс. Самый простой способ его измерить – приложить палец к запястью примерно на 3-5 см ниже сгиба кисти и посчитать частоту пульса за 15 секунд. Умножьте полученный результат на 4, чтобы получить количество сердечных сокращений за одну минуту.
Эту же работу легко проделывают современные фитнес-браслеты и умные часы. Если вы только начали заниматься спортом – эти устройства помогут вам отслеживать дневную активность и ЧСС.
Измерять пульс в процессе нагрузок очень важно: это позволяет понять, как ваше сердце реагирует на физическую активность, и не допустить перегрузок.
У взрослого человека пульс в покое должен варьировать от 60 до 80 ударов. При нагрузке нормой считается показатель до 200 ударов – причем показатель 100-130 ударов в минуту относится к зоне умеренных нагрузок, при которых интенсивно сжигается жир. 130-170 ударов в минуту – это уже интенсивные нагрузки, которые подходят для тренировки сердца. Выше – тренировки высокой интенсивности, которые выступают стрессом для организма. Заниматься с таким пульсом можно только под руководством опытного тренера.
Выше – тренировки высокой интенсивности, которые выступают стрессом для организма. Заниматься с таким пульсом можно только под руководством опытного тренера.
Обратите внимание, что пульс может быть выше, если вы занимаетесь в душном помещении, заболеваете или выпили кофе незадолго до тренировки. В этом случае следите за своим самочувствием – чем выше пульс, тем тяжелее переносится нагрузка.
Зачем рассчитывать ЧСС
Начинающие спортсмены иногда впадают в крайности: они или начинают занятия слишком осторожно, так, что частота пульса при нагрузке почти не отличается от показателя в покое, или же наоборот – начинают заниматься слишком интенсивно. Для организма резкое начало интенсивных нагрузок – большой стресс, и спустя 2-3 недели такого режима человек может серьезно истощить ресурсы организма. Подсчет ЧСС позволяет тренироваться на эффективном и одновременно комфортном для организма уровне.
Артериальное давление и спорт
В норме артериальное давление у человека должно составлять примерно 120\80. Но у людей, которые ведут здоровый образ жизни, давление может быть и ниже – например, в пределах нормы давление 100/60.
Но у людей, которые ведут здоровый образ жизни, давление может быть и ниже – например, в пределах нормы давление 100/60.
Гипертоникам спорт не противопоказан – но им нужно внимательно следить за уровнем нагрузок и начинать занятия в щадящем режиме. Можно начать с ходьбы – сначала приучить себя ходить больше, затем – наращивать темп. Позже можно перейти на бег или плавание.
К тренировкам лучше приступать после консультации с лечащим врачом.
ВАЖНО! Если ваше артериальное давление превышает 190\110 хотя бы периодически, если при физических нагрузках возникает чувство жжения или давления в груди, интенсивные тренировки, к сожалению, вам противопоказаны. Но вы можете заниматься статическими нагрузками, например, йогой.
Зарядка на рабочем месте
Каждый знает о том, что сидячий образ жизни негативно сказывается на здоровье. Недаром большинство офисных работников, которые до 10 часов в день находятся в сидячем положении, имеют заболевания опорно-двигательного аппарата.
Чтобы предотвратить развитие недугов, специалисты рекомендуют каждые два часа производить небольшую разминку на рабочем месте. Выглядит это следующим образом:
- Сначала уделите внимание шее. Медленно вращайте голову вперед-назад, вверх-вниз. Повторите это как минимум 10 раз.
- Затем разомните руки. Поднимите их вверх, скрепите ладони «в замок» и потянитесь как можно выше. Далее сделайте круговые движения плечами, 10 раз.
- Уделите внимание запястьям. Сделайте 15 круговых движений кистями.
- Встаньте на пол, и постарайтесь дотянутся ладонями до стоп, не сгибая колен. Если не получается – тянитесь настолько, насколько можете. Зафиксируйте положение на 15 секунд.
- Сядьте на край стула, вытяните ноги перед собой, не сгибая колен. Держа спину прямо, потяните стопы на себя, а затем назад.
Такой комплекс необходимо осуществлять каждые 2-3 часа на работе.
Подсчет калорий
Если вы хотите не только стать здоровее, но и похудеть, важно уделить внимание питанию. Рацион определяет 70% успеха при снижении веса. Самым эффективным способом похудения является подсчет калорий. Для того, чтобы с точностью их подсчитать, необходимо приобрести кухонные весы. Для подсчета удобно использовать различные приложения – они автоматически рассчитывают калорийность в зависимости от веса продукта. Для поддержания здоровья и комфортного пищеварения взрослый человек должен потреблять около 1700 ккал для женщин и около 2200 ккал для мужчин. Для похудения это число достаточно сократить на 20%.
Рацион определяет 70% успеха при снижении веса. Самым эффективным способом похудения является подсчет калорий. Для того, чтобы с точностью их подсчитать, необходимо приобрести кухонные весы. Для подсчета удобно использовать различные приложения – они автоматически рассчитывают калорийность в зависимости от веса продукта. Для поддержания здоровья и комфортного пищеварения взрослый человек должен потреблять около 1700 ккал для женщин и около 2200 ккал для мужчин. Для похудения это число достаточно сократить на 20%.
Расчет на ударные нагрузки — Доктор Лом
Теоретические предпосылки расчета
Когда мы рассматривали виды нагрузок, то выяснили, что ударная нагрузка является одним из видов динамических нагрузок и отличается от статической нагрузки тем, что при определении максимальных напряжений следует учитывать силы инерции.
Ударной считается нагрузка, прикладываемая в очень короткий промежуток времени. Например, ударная нагрузка возникает при падении одного тела на другое или при быстром изменении давления между рассматриваемыми телами. Все это кажется довольно странным, ведь если тело, например гиря, имеет массу 32 кг, то масса гири не изменится ни до, ни после, ни в момент падения. И это действительно так, но только тогда, когда речь идет о гравитационной массе, однако тщательное исследование явлений окружающего мира показывает, что у любого тела есть еще и инертная или как ее еще называют — инерционная или инерциальная масса. А еще те же исследования показывают, что инертная масса равна гравитационной массе. Так вот, когда речь идет о ударных нагрузках, то создает такую нагрузку не гравитационная, а инертная масса. В общем курсе физики термин «нагрузка» не используется, а используется понятие «сила». И состояние многих материальных тел описывается взаимодействием различных сил. При этом все силы можно условно разделить на внешние и внутренние. В теоретической механике, теории сопротивления материалов, теории упругости, теории прочности и т.п. внешние силы, действующие на рассматриваемую конструкцию, рассматриваются, как нагрузки, а внутренние силы — как напряжения.
Все это кажется довольно странным, ведь если тело, например гиря, имеет массу 32 кг, то масса гири не изменится ни до, ни после, ни в момент падения. И это действительно так, но только тогда, когда речь идет о гравитационной массе, однако тщательное исследование явлений окружающего мира показывает, что у любого тела есть еще и инертная или как ее еще называют — инерционная или инерциальная масса. А еще те же исследования показывают, что инертная масса равна гравитационной массе. Так вот, когда речь идет о ударных нагрузках, то создает такую нагрузку не гравитационная, а инертная масса. В общем курсе физики термин «нагрузка» не используется, а используется понятие «сила». И состояние многих материальных тел описывается взаимодействием различных сил. При этом все силы можно условно разделить на внешние и внутренние. В теоретической механике, теории сопротивления материалов, теории упругости, теории прочности и т.п. внешние силы, действующие на рассматриваемую конструкцию, рассматриваются, как нагрузки, а внутренние силы — как напряжения. При этом предполагается, что сумма внешних сил равна сумме внутренних сил, это в итоге и позволяет составлять уравнения равновесия для рассматриваемой системы.
При этом предполагается, что сумма внешних сил равна сумме внутренних сил, это в итоге и позволяет составлять уравнения равновесия для рассматриваемой системы.
Когда тело, создающее нагрузку, очень долго взаимодействует с телом, в котором под воздействием этой нагрузки возникают напряжения, то скорость обоих тел, точнее центров тяжести обоих тел, при таком взаимодействии согласно принятой системы отсчета практически не изменяется. Это позволяет рассматривать нагрузку и напряжения, как статические, т.е. обусловленные гравитационным взаимодействием. При ударе в зависимости от массы соударяемых тел, скорость одного из тел или обоих тел изменяется очень сильно и в сравнительно короткий промежуток времени. Одной из характеристик тела, двигающегося с некоторой скоростью, является импульс:
p = mиv (288.1)
В данном случае в виду имеется именно инертная масса, и рассматривается поступательное (прямолинейное) движение, т.е. такое движение, для корректного описания которого достаточно рассматривать движение только одной материальной точки, совпадающей с центром тяжести рассматриваемого тела. Для характеристики вращательного движения используются понятия момента инерции и угловой скорости, для сложного движения материальных точек изгибаемой конструкции — коэффициент жесткости, определяющий характер движения различных материальных точек, входящих в состав изгибаемой конструкции в зависимости от значений момента инерции, модуля упругости материала, действующей нагрузки и длины изгибаемой конструкции.
Для характеристики вращательного движения используются понятия момента инерции и угловой скорости, для сложного движения материальных точек изгибаемой конструкции — коэффициент жесткости, определяющий характер движения различных материальных точек, входящих в состав изгибаемой конструкции в зависимости от значений момента инерции, модуля упругости материала, действующей нагрузки и длины изгибаемой конструкции.
Когда тела сталкиваются с относительно большой скоростью, то из-за изменения скорости в течение короткого промежутка времени возникает ударная сила, точнее две ударные силы, одинаковые по значению и направленные противоположно. Таким образом рассматриваемая система сил по прежнему остается в равновесии:
Рисунок 1. Равновесие сил рассматриваемой системы.
Если рассматривать тело, создавшее ударную нагрузку, то на него будет действовать ударная сила, равная сумме опорных реакций, показанных на рисунке 1.б) и равная — Qу, т. е. направленная противоположно. Однако строителей очень редко интересует судьба падшего тела, им необходимо обеспечить прочность конструкции после удара, т.е. рассчитываемая конструкция должна работать только в области упругих, восстанавливаемых со временем деформаций, а неупругие деформации, могут привести к разрушению конструкции.
е. направленная противоположно. Однако строителей очень редко интересует судьба падшего тела, им необходимо обеспечить прочность конструкции после удара, т.е. рассчитываемая конструкция должна работать только в области упругих, восстанавливаемых со временем деформаций, а неупругие деформации, могут привести к разрушению конструкции.
Теоретически, если известно время t, в течение которого импульс будет передаваться от одного тела другому, определить ударную силу не проблема, так как
Qу = mиv/t (288.2)
и тогда расчет конструкции можно просто выполнить на действие ударной силы, т.е. по расчетной схеме, показанной на рисунке 1.б). Да вот беда, время, в течение которого импульс передается от одного тела другому, зависит от множества различных факторов (о которых речь ниже) и может измеряться в пределах от микросекунд до секунд. Потому точно определить значение времени, а значит и ударной силы достаточно сложно.
Далее, в процессе удара кинетическая энергия упавшего тела частично трансформируется в потенциальную энергию деформации рассматриваемой конструкции. Например балка, показанная на рисунке 1, прогнется, при этом в момент, когда значение деформации, будет максимальным, скорость движения центра тяжести балки будет равной нулю, а значит систему можно рассматривать как статическую. Вот только упавшее тело, если оно все еще находится на балке, уже не будет создавать ударную нагрузку, а только обычную статическую, поэтому внутренние напряжения начнут уменьшаться, а значит, и величина деформации будет уменьшаться. А в результате действия инерциальных сил, возникающих как при движении груза, так и при движении частиц рассматриваемой конструкции такое движение превратится в колебательное, со временем затухающее из-за перехода части кинетической и потенциальной энергии в тепловую.
Кроме того часть энергии удара преобразуется в звуковые колебания и если верить индийским фильмам, то в звук преобразуется чуть ли не вся энергия удара. Так же при ударе часть энергии переходит в упругие и неупругие деформации падающего тела и местные неупругие деформации рассматриваемого элемента конструкции, а потому точное решение задачи о возникающих при ударе внутренних напряжениях и деформациях материала конструкции с учетом вышеприведенных факторов является не простой задачей. Однако в точном решении задач не всегда есть необходимость и потому в строительной практике получили распространение приближенные методы расчета.
Так же при ударе часть энергии переходит в упругие и неупругие деформации падающего тела и местные неупругие деформации рассматриваемого элемента конструкции, а потому точное решение задачи о возникающих при ударе внутренних напряжениях и деформациях материала конструкции с учетом вышеприведенных факторов является не простой задачей. Однако в точном решении задач не всегда есть необходимость и потому в строительной практике получили распространение приближенные методы расчета.
Максимально упростить решение подобных задач помогают следующие допущения и физические модели процесса:
1. Любую балку, плиту, стену, колонну или другую строительную конструкцию можно рассматривать как упругую систему с одной степенью свободы. Этим подразумевается, все деформации будут находиться в области упругих, т.е. восстанавливаемых со временем и то, что колебания будут происходить только относительно одной из осей. Например, при падении тела на рассматриваемую конструкцию под действием силы тяжести перемещение падающего тела происходит только вдоль оси у, возможные смещения тела вдоль осей х и z не учитываются. Некая тело с массой m, соединенное с упругой пружиной, является простейшей линейной механической моделью упругой системы с одной степенью свободы:
Некая тело с массой m, соединенное с упругой пружиной, является простейшей линейной механической моделью упругой системы с одной степенью свободы:
Рисунок 2. Амплитуда колебаний
2. Амплитуда колебаний, определяющая максимальное отклонение рассматриваемой точки вдоль оси у, соответствует максимальной деформации рассматриваемой конструкции. При продольном ударе — это относительное изменение длины Δl, при изгибающем ударе — прогиб f, при вращающем ударе — угол поворота φ (далее мы будем рассматривать в основном изгибающий удар). При рассмотрении колебательного движения физических тел, двигающихся по прямолинейной траектории, рассматриваемая точка, совершающая колебания, соответствует центру тяжести тела, если масса изгибаемой конструкции пренебрежимо мала, по сравнению с массой ударяющего тела, то для упрощения расчетов массой изгибаемой конструкции можно пренебречь и рассматривать колебания согласно принятой физической модели (рисунок 2).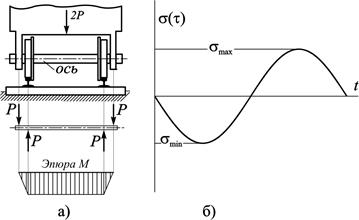
3. Так как колебания системы, вызванные ударом, являются затухающими из-за сопротивления окружающей среды (как минимум воздуха) и наличия сил внутреннего трения, постепенно переводящих часть энергии удара в нагрев, то максимальная амплитуда, соответствующая максимальной деформации, будет только в течение первого периода колебания. Таким образом расчет сводится к определению максимально возможной амплитуды в течение первого периода колебания.
4. Деформации рассматриваемого элемента конструкции от ударяющего тела распространяются по всей длине элемента, подчиняются закону Гука и пропорциональны деформациям, которые возникают при статическом приложении нагрузки от того же тела и в том же месте, т.е. расчетные схемы, показанные на рисунке 1, могут использоваться для расчета рассматриваемой конструкции.
5. Пропорциональность динамических и статических деформаций δ определяется динамическим коэффициентом удара kд, соответственно пропорциональность динамических и статических напряжений σ также определяется динамическим коэффициентом:
δд = kдδст (288. 3.1)
3.1)
σд = kдσст (288.3.2)
соответственно
Qд = kдQст (288.3.3)
Мд = kдМст (288.3.4)
и так далее.
6. Предполагается, что падающее тело имеет жесткость значительно больше жесткости рассматриваемого элемента конструкции. Это позволяет не учитывать величину упругих деформаций падающего тела при ударе и соответственно исключает развитие неупругих деформаций в упавшем теле. Соответственно время, в течение которого импульс от одного тела передается другому будет минимальным, а значит и значение ударной силы будет максимально возможным. И даже если на железную балку падает железная гиря, имеющая вполне определенную жесткость, то для упрощения расчетов упругие и возможные неупругие деформации гири не учитываются. Результат такого допущения — дополнительный запас по прочности.
7. Предполагается, что падающее тело с момента прикосновения к рассматриваемому элементу конструкции продолжает движение с такой же скоростью, с какой перемещается поперечное сечение элемента под телом в результате развития деформаций, т.е. упавшее тело как бы прилепляется к рассматриваемому элементу и не отскакивает до момента развития максимальных деформаций. Такое допущение справедливо лишь тогда, когда масса упавшего тела не меньше массы элемента. А если масса рассматриваемого элемента пренебрежимо мала по сравнению с массой падающего тела, то в момент столкновения изменением скорости вообще можно пренебречь и рассматривать изменение скорости упавшего тела после столкновения только как результат изменения потенциальной энергии деформации и тогда принятая физическая модель будет наиболее полно соответствовать реальному процессу. Если масса рассматриваемого элемента равна или больше массы падающего тела, то такое допущение также приводит к дополнительному запасу по прочности.
Предполагается, что падающее тело с момента прикосновения к рассматриваемому элементу конструкции продолжает движение с такой же скоростью, с какой перемещается поперечное сечение элемента под телом в результате развития деформаций, т.е. упавшее тело как бы прилепляется к рассматриваемому элементу и не отскакивает до момента развития максимальных деформаций. Такое допущение справедливо лишь тогда, когда масса упавшего тела не меньше массы элемента. А если масса рассматриваемого элемента пренебрежимо мала по сравнению с массой падающего тела, то в момент столкновения изменением скорости вообще можно пренебречь и рассматривать изменение скорости упавшего тела после столкновения только как результат изменения потенциальной энергии деформации и тогда принятая физическая модель будет наиболее полно соответствовать реальному процессу. Если масса рассматриваемого элемента равна или больше массы падающего тела, то такое допущение также приводит к дополнительному запасу по прочности.
8. Явление удара рассматривается с позиций закона сохранения энергии и соответственно сохранения импульсов. При этом предполагается, что кинетическая энергия Т1 падающего тела — груза в момент удара полностью превращается в потенциальную энергию Uд2 деформации конструкции и кинетическую энергию Т’2 движения рассматриваемой конструкции:
Явление удара рассматривается с позиций закона сохранения энергии и соответственно сохранения импульсов. При этом предполагается, что кинетическая энергия Т1 падающего тела — груза в момент удара полностью превращается в потенциальную энергию Uд2 деформации конструкции и кинетическую энергию Т’2 движения рассматриваемой конструкции:
Е = Т1 = Uд2 + Т’2 (288.4.1)
Это допущение справедливо только при рассмотрении столкновения двух равноупругих тел имеющих равную массу, при этом одно из тел до момента столкновения находится в состоянии покоя, т.е. его скорость равна нулю. Поэтому количество кинетической энергии рассматриваемой конструкции Т2 принимается равным нулю, а также принимается равным нулю количество кинетической энергии Т’1 падающего тела сразу после момента столкновения, так как скорость падающего тела в момент столкновения обнуляется.
Если масса рассматриваемого элемента конструкции пренебрежимо мала по сравнению с массой ударяющего тела, то величиной Т2 для упрощения расчетов можно пренебречь и рассматривать изменение кинетической энергии падающего тела как изменение потенциальной энергии деформации рассматриваемого элемента:
Т = Uд (288.4.2)
Это допущение, не учитывающее переход части энергии в звуковую, тепловую и другие воды энергии также дает дополнительный запас по прочности.
Принятие этих допущений позволяет значительно упростить расчет конструкций и даже обеспечить дополнительный запас по прочности для колонны, стойки, балки, плиты и любого другого рассматриваемого элемента конструкции при использовании физической модели, показанной на рисунке 2.
В зависимости от направления удара по отношению к оси рассматриваемого элемента конструкции и характера происходящих деформаций удары рассматриваются как продольный — приводящий к растяжению или сжатию рассматриваемого элемента (колон, стоек, стен, свай), поперечный — вызывающий деформации изгиба (поперечный удар часто называют изгибающим ударом) характерен для стержней, балок, плит перекрытия, и крутильный удар — вызывающий деформации кручения в валах машин и механизмов или в балках при внецентренном приложении ударной нагрузки.
Теория расчета на динамическую нагрузку
Согласно основному закону динамики — второму закону Ньютона — любое тело, имеющее некоторую массу m и движущееся с ускорением свободного падения g = 9.81 м/с2, может рассматриваться как сила Q = mg, а при расчете строительных конструкций внешние силы, как уже говорилось, рассматриваются, как нагрузка. Именно поэтому в формулировке задач по расчету строительных конструкций нагрузки от тел, имеющих некоторую массу m, измеряемую в понятных простому человеку килограммах или тоннах , указываются в не столь хорошо известных и понятных Ньютонах и килоНьютонах. Теоретически это правильно, но вполне допустимо при выполнении расчетов заменять Ньютоны на килограмм-силы. Например, человека весом в 100 кг, можно рассматривать как сосредоточенную нагрузку Q = 1000 Н = 100 кгс или просто 100 кг. При этом уменьшение значения, возникающее при умножении массы на 9. 81 обычно не учитывается, что опять таки приводит к дополнительному запасу по прочности.
81 обычно не учитывается, что опять таки приводит к дополнительному запасу по прочности.
При этом даже если человек стоит абсолютно неподвижно в течение долгого времени, т.е. скорость его перемещения в рассматриваемой системе отсчета равна нулю, то он все равно создает нагрузку, в данном случае статическую. Этот парадокс устраняется тем, что если опору из под человека убрать, то он полетит к центру Земли, причем с ускорением, мало отличающимся от ускорения свободного падения и значит опора может рассматриваться как такая же сила, только действующая в противоположную сторону, и называется эта сила опорной реакцией. А когда опорная реакция равна опорной силе, то система находится в состоянии равновесия, т.е. никуда не движется (во всяком случае в принятой системе отсчета). При рассмотрении стержней и балок, имеющих две опоры, таких опорных реакций будет две (см. рисунок 1).
Однако все это справедливо только для абсолютно жестких тел. Реальные же тела и в частности строительные конструкции под воздействием нагрузки деформируются, а значит и человек, представляющий собой нагрузку, будет перемещаться в пространстве на величину этой деформации.
Как определяются деформации для сжатых, растянутых и изгибаемых элементов, и при чем тут момент инерции, мы уже знаем, осталось только добавить, что при расчете деформаций от действия статической нагрузки предполагается, что статическая нагрузка прикладывается не моментально, а очень медленно, т.е. значение нагрузки постепенно нарастает от нуля до максимального значения за время, значительно превышающее время деформации. Таким образом скорость перемещения в пространстве тела, создающего нагрузку, стремится к нулю и получается, что наблюдаемые в результате воздействия нагрузки деформации, например вот такие:
Фотография 174.1. Прогиб балки — линейки при действии статической нагрузки — мерного стакана
это результат действия только гравитационной массы тела, создающего нагрузку. Дальнейшее описание будет производиться на примере балки линейки для наглядности.
Если приложить нагрузку мгновенно, например, если поставить мерный стакан на линейку и сразу его отпустить, то прогиб будет значительно больше. Потому что стакан, опускаясь вместе с прогибающейся линейкой, на определенном этапе приобретет достаточно большую скорость, а значит, при расчетах нужно учитывать не только гравитационную, но и инертную массу тела, а также инертную массу рассматриваемой конструкции. Так как физиками до сих пор считается, что гравитационная масса равна инертной (во всяком случае попытки опровергнуть это утверждение пока ни к чему не привели), то вполне логично предположить, что инертная масса приведет к такой же деформации как и гравитационная масса, а значит деформация от динамической нагрузки будет в 2 раза больше, чем от статической нагрузки, создаваемой тем же телом. В математическом выражении это предположение с учетом теоретических предпосылок (т.е. без учета массы линейки) выглядит так:
Потому что стакан, опускаясь вместе с прогибающейся линейкой, на определенном этапе приобретет достаточно большую скорость, а значит, при расчетах нужно учитывать не только гравитационную, но и инертную массу тела, а также инертную массу рассматриваемой конструкции. Так как физиками до сих пор считается, что гравитационная масса равна инертной (во всяком случае попытки опровергнуть это утверждение пока ни к чему не привели), то вполне логично предположить, что инертная масса приведет к такой же деформации как и гравитационная масса, а значит деформация от динамической нагрузки будет в 2 раза больше, чем от статической нагрузки, создаваемой тем же телом. В математическом выражении это предположение с учетом теоретических предпосылок (т.е. без учета массы линейки) выглядит так:
— для статической нагрузки kд = 1
— для динамической нагрузки kд = 1 + 1 = 2
Впрочем, такой метод определения динамического коэффициента при мгновенном приложении нагрузки может показаться слишком простым. Что ж, устранить эту проблему не сложно. Для начала вернемся к п.2 и 3 теоретических предпосылок и рассмотрим их более детально.
Что ж, устранить эту проблему не сложно. Для начала вернемся к п.2 и 3 теоретических предпосылок и рассмотрим их более детально.
В общем виде уравнение гармонических колебаний, позволяющее определить значение отклонения по оси у — что в нашем случае соответствует величине деформации f, выглядит так:
Рисунок 3. Амплитуда колебаний, как радиус окружности и гипотенуза прямоугольного треугольника
у = Аsinφ = Asin(φo + ωt) (288.5.1)
где φ = φo + ωt — фаза колебания, соответственно φo — начальная фаза колебания при t =0.
При этом амплитуда рассматривается, как радиус окружности, а фаза колебаний, как угол наклона этого радиуса, что в итоге и дает нам синусоиду для исследуемой точки, показанную на рисунке 2. Так как скорость материальной точки является производной расстояния по времени, то
y’ = v = (Asin((φo + ωt))’ = Aωcos(φo + ωt) (288. 5.2)
5.2)
тогда значение амплитуды по оси х можно рассматривать как t = v/ω. Ну а дальше из установленных Архимедом соотношений сторон прямоугольного треугольника, образованного катетами х и у и гипотенузой А, следует, что:
А = √¯(у2 + х2) = √¯(у2 + (v/ω)2) (288.5.3)
Если придать этой легкой математической формуле тяжелый физический смысл, то получается, что максимальное значение отклонения по оси у, а в нашем случае величина деформации f, будет максимальным, когда скорость материальной точки — стакана будет равна нулю и соответственно максимальная скорость у материальной точки будет в моменты, когда деформация будет равна нулю. Причина этого — в воздействии сил инерции. Так как нас интересует только максимальное значение отклонения, равное амплитуде, т.е. у = А, т. е. при скорости материальной точки, равной нулю, то формулу (288.5.3) можно с учетом этого преобразовать в:
е. при скорости материальной точки, равной нулю, то формулу (288.5.3) можно с учетом этого преобразовать в:
А = √‾(yи2) (288.5.4)
где уи — максимальное значение деформации при действии сил инерции. При этом полное значение деформации с учетом действия гравитационных сил (на примере линейки) составит:
fп = fг + fи = 2fг = 2fи = fг + √¯(fг2) (288.6.1)
Так как прогиб от действия инертной массы равен прогибу от действия гравитационной массы.
Соответственно динамический коэффициент составит
kд = 1 + 1 = 1 + √¯(12) = 2 (288.6.2)
Если вернуться к математической модели, то мы как бы смещаем вниз по оси у синусоиду (рисунок 2) или окружность (рисунок 3) на значение уг, равное уи, и таким образом получаем полное значение деформации в точках экстремума функции.
Таким образом человек, который ходит по помещению и при этом достаточно быстро перебирает ногами, перенося свой вес с одной ноги на другую, создает как минимум динамическую нагрузку и потому при расчете конструкций перекрытия на нагрузку от такого человека статическую нагрузку, создаваемую гравитационной массой человека, следует умножать на динамический коэффициент kд = 2. При этом высота падения и соответственно скорость падения в момент столкновения принимаются равными нулю.
Теория расчета на ударную нагрузку
До этого мы рассматривали деформацию тела (балки) под действием динамической нагрузки, т.е. в ситуации, когда скорость груза в момент касания с конструкцией равна нулю. Если же груз будет падать с некоторой высоты, то в момент касания с конструкцией эта скорость не будет равна нулю (при принятой нами массе балки значительно меньшей, чем масса груза) и тогда для определения амплитуды теоретически можно использовать формулу (288.3.3). Вот только для этого придется сначала определить значение скорости в момент удара.
Вот только для этого придется сначала определить значение скорости в момент удара.
Скорость тела, падающего с ускорением свободного падения, без учета влияния сопротивления окружающей среды в любой момент времени можно определить по формуле:
v = √¯(vo2 + 2gh) (288.7.1)
где h — высота падения, м.
Если начальная скорость vo = 0, то формула (288.6.1) примет вид
v = √(2gh) (288.7.2)
Теперь попробуем определить значение циклической частоты ω (или угловой скорости — это кому как больше нравится). Так как ускорение — это вторая производная расстояния по времени, то:
y» = a = (Asin((φo + ωt))» = — Aω2sin(φo + ωt) (288.8)
Физический смысл этой формулы в том, что ускорение движения тела а, подобно скорости v и величине смещения y, подчиняется гармоническому закону, но колебания ускорения на полпериода (на угол П) расходятся с колебаниями смещения и находятся как бы в противофазе смещению. То есть когда смещение (в нашем случае прогиб f) максимально, то ускорение а также максимально, но направлено в сторону, противоположную смещению. Так же здесь заметим, что колебания скорости смещены на четверть периода или на угол П/2, по отношению к колебаниям смещения.
То есть когда смещение (в нашем случае прогиб f) максимально, то ускорение а также максимально, но направлено в сторону, противоположную смещению. Так же здесь заметим, что колебания скорости смещены на четверть периода или на угол П/2, по отношению к колебаниям смещения.
Таким образом из формул (288.3.1) и (288.7) можно вывести уравнение гармонических колебаний:
a/ω2 + y = 0 или у» + ω2y = 0 (288.9)
соответственно
ω2 = — [a/y] или ω2 = Q/my = g/yи (288.10.1)
В данном случае имеется в виду инертная масса груза, а масса балки не учитывается. Тогда согласно формул (288.5.3), (288.7.2) и (288.10.1)
у = √¯(уи2 + 2ghyи/g) = √¯(уг2 + 2hyг) (288.11.1)
Тогда полное значение деформации составит:
уп = уг + √¯(уг2 + 2hyг) (288. 11.2)
11.2)
тогда
kд = уп/уг = 1 + √1 + 2h/yг = 1 + √1 + 2h/уст (288.11.3)
Как правило никакой разницы между деформациями от динамической и ударной нагрузки не делается, а динамическая нагрузка рассматривается как частный случай ударной нагрузки, при которой скорость падающего груза в момент контакта с рассматриваемой конструкцией равна нулю, понятие «ударный коэффициент» — не используется, величина деформации от действия гравитационной массы обозначается как статическая деформация уст. Сути дела это не меняет, но упомянуть об этом стоит, равно как и о том, что формулы (288.11) можно вывести и другими способами. Здесь же приведен, возможно и не самый простой, но по моему мнению самый наглядный способ. И еще, если присмотреться, то формулы для определения скорости, вертикального смещения, и многих других не приведенных здесь параметров, достаточно похожи, а роднит их принцип определения гипотенузы прямоугольного треугольника. Вот такие дела.
Вот такие дела.
Если вернуться к математической модели, то при определении амплитуды при ударной нагрузке мы рассматривали как бы не всю, а только нижнюю часть синусоиды, при этом амплитуда рассматриваемой синусоиды соответствует амплитуде колебаний, создаваемой при динамической нагрузке грузом, имеющим массу, умноженную на динамический коэффициент.
Для упрощения расчетов при h/yст > 10 единицей в подкоренном выражении можно пренебречь и тогда формула (288.11.3) примет вид:
kд = 1 + √2h/уст (288.11.4)
А если h/yст > 100, то можно не учитывать и единицу перед квадратным корнем, тогда:
kд = √2h/уст (288.11.5)
Пример расчета балки на ударную нагрузку
Имеется шарнирно закрепленная балка перекрытия длиной 4 м из древесины сечением 20х10 см. На средину балки с высоты 50 см падает гиря весом в 32 кг. Требуется определить прочность балки при ударной нагрузке.
Требуется определить прочность балки при ударной нагрузке.
1. Определим прогиб балки при воздействии статической нагрузки
fcт = Ql3/48EI = 32х4003/(48х100000х6666.667) = 0.064 см
где Е = 105 кгс/см2 — модуль упругости древесины, I = bh3/12 = 6666.667 см4 — момент инерции поперечного сечения.
2. Если определять динамический коэффициент с учетом того, что высота падения значительно больше статического прогиба, то
kд = 1 + √(2х50/0.064) = 40.53
3. Тогда максимальный прогиб составит
fд = 0.064х40.53 = 2.59 см
4. Это достаточно большой прогиб, но намного важнее выяснить, выдержит ли такую ударную нагрузку балка
Мд = Qlkд/4 = 32х400х40.53/4 = 129696 кг·см
5. Тогда при расчетном сопротивлении R = 140 кг/см2 требуемый момент сопротивления составит
Wтр = М/R = 129696/140 = 926. 4 см3
4 см3
6. Момент сопротивления для балки сечением 20х10 см составит W = 2I/h = 6666.667/10 = 666.67см3 < Wтр = 926.4 см3.
Вывод: балка под действием такой ударной нагрузки разрушится.
Пример расчета балки на ударную нагрузку от груза, падающего не посредине балки
Имеется все та же шарнирно закрепленная балка перекрытия длиной 4 м из древесины сечением 20х10 см. На расстоянии 1 м от опоры балки с той же высоты 50 см падает все та же гиря весом в 32 кг. Требуется определить прочность балки при ударной нагрузке.
1. Определим прогиб балки в месте падения груза при воздействии статической нагрузки
fcт = Qа2b2/3lEI = 32х1002x3002/(3х400×100000х6666.667) = 0.036 см
kд = √2х50/0.036 = 52.7
как видим, за счет смещения места падения груза к одной из опор динамический коэффициент даже увеличился, но нас по прежнему интересует прочность балки
Мд = Qabkд/l = 32х100×300х52. 7/400 = 126491 кг·см
7/400 = 126491 кг·см
так как максимальное значение изгибающего момента почти не изменилось, то и без дальнейших расчетов понятно, что балка такую ударную нагрузку не выдержит. А вот если груз упадет очень близко к одной из опор, например на расстоянии 10 см, то
fcт = Qа2b2/3lEI = 32х102x3902/(3х400×100000х6666.667) = 0.00061 см
kд = √2х50/0.00061 = 405.42
Мд = Qabkд/l = 32х10×390х229.4/400 = 126491 кг·см
Вывод: на каком бы расстоянии от опоры ни упал груз, балка под действием такой ударной нагрузки разрушится.
Пример расчета балки на ударную нагрузку с учетом жесткости падающего груза
Как видим, если рассматривать соударение балки с гирей, как абсолютно жестким телом, то у балки никаких шансов на выживание нет, она разрушится. Однако любое физическое тело имеет вполне определенную жесткость, а это значит, что такое тело будет также деформироваться. А значит, время контакта при столкновении двух тел из-за упругих и возможных неупругих деформаций ударяющего тела будет больше и соответственно ударная сила, действующая на балку, будет меньше. Это подтверждают эксперименты со сталкивающимися телами из любых материалов. Например, когда относительно легкий стальной шарик падает на очень массивную стальную пластину, то теоретически после соударения относительно легкий металлический шарик должен отскочить от очень массивной пластины на высоту, примерно равную высоте, с которой шарик упал. Однако в реальности высота отскока значительно меньше, и разница доходит до 3 раз. На основании этого можно определить коэффициент восстановления:
А значит, время контакта при столкновении двух тел из-за упругих и возможных неупругих деформаций ударяющего тела будет больше и соответственно ударная сила, действующая на балку, будет меньше. Это подтверждают эксперименты со сталкивающимися телами из любых материалов. Например, когда относительно легкий стальной шарик падает на очень массивную стальную пластину, то теоретически после соударения относительно легкий металлический шарик должен отскочить от очень массивной пластины на высоту, примерно равную высоте, с которой шарик упал. Однако в реальности высота отскока значительно меньше, и разница доходит до 3 раз. На основании этого можно определить коэффициент восстановления:
kв = √h’/h (288.12)
где h’ — высота отскока, а h — высота падения.
Этот коэффициент будет показывать, насколько уменьшится ударная сила с учетом упругих свойств падающего груза и тогда
kуд = 1 + √1 +2h’/fстили kyд = kдkв (288. 13)
13)
ниже приведены значения коэффициента восстановления для некоторых веществ:
Таблица 1. Коэффициенты восстановления при частично упругом соударении тел
| Вещество | k |
| Древесина | 0.5 |
| Пробка | 0.55 |
| Сталь | 0.55 |
| Слоновая кость | 0.889 |
| Стекло | 0.9375 |
Помимо всего прочего изучение этой таблицы позволяет понять, почему раньше для изготовления бильярдных шаров использовалась именно слоновая кость. Но в данном случае нас интересует сталь, точнее гиря изготовленная с применением железа. Конечно же на значение коэффициента восстановления будет влиять геометрическая форма падающего тела, и чем ближе эта форма к шару тем ближе значение коэффициента восстановления к указанному в таблице. Поэтому значение коэффициента восстановления следует дополнительно умножить на поправочный коэффициент kп = 0.5 — 1, учитывающий форму падающего тела в зависимости от материала сталкивающихся тел. Определение более точного значения поправочного коэффициента — отдельная большая тема. Однако для упрощения расчетов лучше не уменьшать значение коэффициента восстановления, а наоборот увеличить, умножив на коэффициент надежности по нагрузке γ = 1.1 — 1.3.
Поэтому значение коэффициента восстановления следует дополнительно умножить на поправочный коэффициент kп = 0.5 — 1, учитывающий форму падающего тела в зависимости от материала сталкивающихся тел. Определение более точного значения поправочного коэффициента — отдельная большая тема. Однако для упрощения расчетов лучше не уменьшать значение коэффициента восстановления, а наоборот увеличить, умножив на коэффициент надежности по нагрузке γ = 1.1 — 1.3.
Например, при столкновении железной гири с деревянной балкой можно использовать коэффициент γ = 1.2 и тогда:
kд = 40.53х0.55х1.2 = 26.75
тогда максимальный прогиб составит
fд = 0.064х26.75 = 1.71 см
Мд = Qlkд/4 = 32х400х26.75/4 = 85600 кг·см
Wтр = М/R = 85600/140 = 611.4 см3
момент сопротивления W = 6666.667/10 = 666.67см3 > Wтр = 611. 4 см3.
4 см3.
Вывод: балка выдержит такую ударную нагрузку, однако существует очень высокая вероятность того, что после удара на поверхности балки останется порядочная вмятина, а выражаясь научным языком, изменятся размеры поперечного сечения балки, что приведет к изменению несущей способности балки. Поэтому даже если балка и выдержит один удар, то нет никакой гарантии, что балка выдержит много ударов и такую балку желательно избавить от такого насилия. Обычно это происходит по умолчанию, когда на балки перекрытия укладываются доски напольного покрытия. И тогда в результате падения тяжелых грузов с относительно большой высоты будет страдать уже не балка, а точнее не только балка, но и доски, а если это доски чернового пола, то покрытие по черновому полу. А потому обычно выполняется дополнительная защита пола в местах, где падение груза на перекрытие достаточно вероятно. Принцип такой защиты прост — чем толще защитное покрытие и чем меньше модуль упругости материала защитного покрытия, тем меньше будет в итоге ударная сила, действующая на конструкции перекрытия. Да и поменять защитное покрытие намного быстрее и дешевле, чем балки или плиты перекрытия.
Да и поменять защитное покрытие намного быстрее и дешевле, чем балки или плиты перекрытия.
Кстати на эффекте развития местных неупругих деформаций основаны различные методы неразрушающих методов определения прочности бетона, в частности для этого может использоваться молоток Кашкарова, но это уже совсем другая тема.
И еще, борцы тоже не любят бороться на жестком бетонном полу, а все больше на специальных покрытиях и вовсе не потому, что заботятся о надежности перекрытия, в этом случае за основу берется прочность главной несущей конструкции человеческого организма — скелета и в частности черепа.
2.Расчет и выбор подшипников
06.04.2018
2.Расчет и выбор подшипников
Подшипники для вибрационных машин, как правило, рассчитываются для номинальной долговечности Lh от 10 000 до 20 000 часов.
Уравнение для расчeта:
Lh = (C/P)p • 106/(n • 60) [ч]
C — динамическая грузоподъемность [кН], см. таблицы-спецификации
таблицы-спецификации
P — эквивалентная динамическая нагрузка [кН], см. разделы 2.1 — 2.3
p = 3,33 — показатель степени для расчета долговечности роликоподшипников
n — частота вращения [мин-1]
При вычислении эквивалентной динамической нагрузки подшипника P влияние недостаточно точноопределимых параметров учитывается посредством домножения радиальной нагрузки Fr на коэффициент запаса fz = 1,2. Практика показывает, что с использованием данной методики достигается достаточный срок службы подшипника.
Для более точных результатов вычисляют скорректированную (модифицированную) долговечность согласно DIN ISO 281, приложение 1 (см. каталог WL 41700). Требуемая для расчета грузоподъемность по усталостной прочности См приводится в таблицах-спецификациях.
2.1 Вибровозбудитель с круговыми колебаниями
Рис. 3 иллюстрирует принцип вибровозбудителя с круговыми вибрациями с дисбалансом.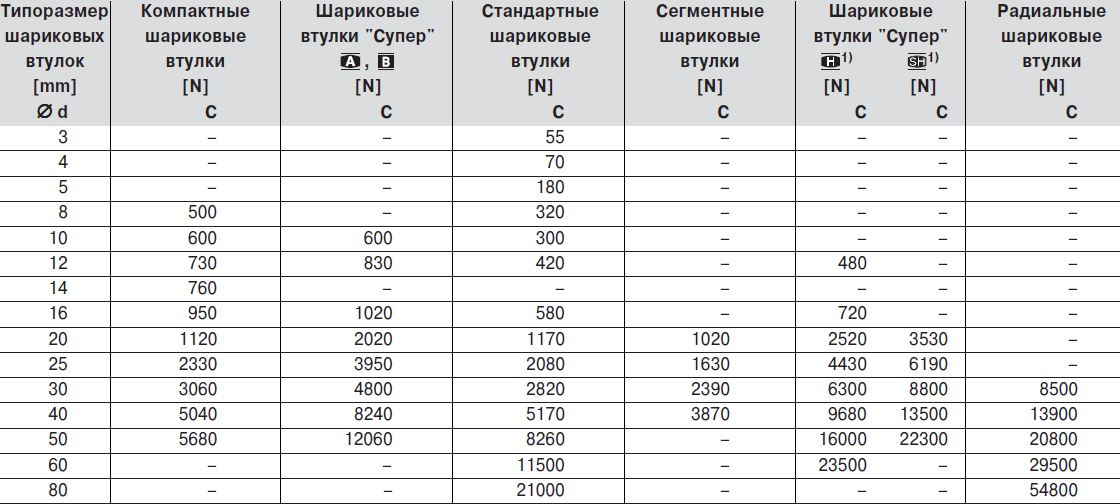 Нагрузка на подшипник определяется центробежной силой короба виброгрохота, радиусом вибраций и скоростью вращения в соответствии с формулой:
Нагрузка на подшипник определяется центробежной силой короба виброгрохота, радиусом вибраций и скоростью вращения в соответствии с формулой:
Fr — радиальная нагрузка [кН]
m — масса короба [кг]
r — радиус вибрации [м]
м — угловая скорость [1/с]
G — вес короба [кН]
g — ускорение свободного падения [9,81 м/с2]
n — частота вращения [мин-1]
z — количество подшипников
Радиус вибрации вибровозбудителя с круговыми колебаниями можно определить из соотношения веса короба и веса вибровозбудителя.
Так как вибровозбудители работают, как правило, в сверхкритическом режиме, и почти достигается статическая амплитуда вибраций, можно считать неизменной общую ось центра тяжести обеих масс (короба виброгрохота и вибровозбудителя), см. рис. 4. Базируясь на этой предпосылке, справедливо равенство:
Откуда радиус вибраций:
где
G — вес короба виброгрохота
[кН]
G1 — вес вибровозбудителя [кН]
R — расстояние между центром тяжести вибровозбудителя и осью подшипника [м]
r — радиус вибраций короба виброгрохота [м]
Ga • R — момент дисбаланса вибровозбудителя [кН •м]
G + Ga — общий вес, поддерживаемый пружинами [кН]
Подставляя уравнение (2) в (1), путем преобразований получаем радиальную нагрузку на подшипник:
Пример:
Вес короба виброгрохота G = 35 кН
Радиус вибраций r = 0,003 м
Частота вращения n = 1200 мин-1
Число подшипников z = 2
Нагрузка на подшипник определяется в соответствии с уравнением (1)
Эквивалентная динамическая нагрузка, необходимая для определения динамической грузоподъемности подшипника, вычисляется по формуле:
|
Схема вибровозбудителя с круговыми вибрациями |
Радиус вибраций определяется отношением веса короба виброгрохота и веса вибровозбудителя |
2.
 2 Вибровозбудитель с линейными колебаниями
2 Вибровозбудитель с линейными колебаниями
Основой работы вибровозбудителя с линейными колебаниями являются две синхронно вращающиеся в противоположном направлении вибросистемы (см. рис. 5). Для определения сил, вращающиеся векторы центробежных сил раскладываются в проекции на оси в направлении линии, связывающей оба вала, и в направлении, перпендикулярном этой линии. Очевидно, что компоненты, проецируемые на линию, связывающую оба вала, взаимно сокращаются, при этом компоненты в перпендикулярном направлении складываются и генерируют гармонически меняющуюся силу инерции, сообщающую коробу виброгрохота линейные колебания. В силу того что так называемая статическая амплитуда устанавливается из-за сверхкрити- ческих режимов в направлении вибраций и общая ось центра тяжести короба виброгрохота и вибровозбудителей в ходе колебания остается неизменной, нагрузки, действующие на подшипник, вычисляются следующим образом.
В направлении вибрации:
Перпендикулярно к колебательному движению действует несколько большая нагрузка, вычисляемая по формуле:
В отличие от вибровозбудителей с круговыми вибрациями, где нагрузка на подшипник всегда остается неизменно высокой, в вибровозбудителях с линейными колебаними нагрузка дважды меняет свою величину от Fr max до Fr min в течение одного оборота вала с дисбалансом.
Если сравнить равенство (4) и равенство (1), то становится очевидно, что минимальная нагрузка на подшипник вибровозбудителя с линейными колебаниями равна минимальной нагрузке на подшипник аналогичного вибровозбудителя с круговыми колебаниями.
Для вибровозбудителя величина нагрузки синусоидального характера, действующая на подшипник, определяется по формуле
В то время как в вибровозбудителе с круговыми колебаниями для определения нагрузки на подшипник достаточно знать вес короба виброгрохота G, радиус колебаний r и частоту вращения n, в случае с вибровозбудителем с линейными колебаниями этих данных будет достаточно только для определения минимальной действующей нагрузки.
Для более точных расчетов необходимо знать дополнительно или вес вибровозбудителя Gr или расстояние R между центрами тяжести вибровозбудителя и соответствующих осей подшипника. Тогда для определения неизвестной величины возможно использование следующей формулы:
Пример:
Вес короба виброгрохота G = 33 кН Вес вибровозбудителя Ga = 7,5 кН Амплитуда r = 0,008 м Частота вращения n = 900 мин-1 Количество подшипников z = 4
После определения в соответствии с (4) и (5) находим
Нагрузка на подшипник:
Эквивалентную динамическую нагрузку, необходимую для вычисления динамической грузоподъемности подшипника, определяют по формуле:
|
|
2.
 3 Эксцентриковый виброгрохот
3 Эксцентриковый виброгрохот
В отличие от вибровозбудителя на пружинах, при использовании вибро¬машин с вибровозбудителем с жестким креплением радиус вибраций определяется эксцентриситетом вала. Как и в случае с вибровозбу¬дителем с круговыми колебаниями, нагрузка на подшипники вычисляется:
где r — это эксцентриковый радиус коленвала и z — число внутренних подшипников (рис. 6).
Влиянием опорных пружин на нагрузку внутренних подшипников можно пренебречь. На внешние подшипники эксцентрикового виброгрохота действует небольшая нагрузка, т.к. центробежная сила, действующая на короб виброгрохота, на холостом ходу компенсируется противовесами (G2). Нагрузка на эти подшипники непостоянна; она изменяется по синусоиде из-за опорных пружин.
В процессе работы баланс масс в машине нарушается из-за наличия просеиваемых материалов, из-за чего внешние подшипники несут дополнительную нагрузку.
В любом случае эта дополнительная нагрузка крайне мала.
При выборе подшипников ориентируются на диаметр вала.
При этом находятся подшипники, грузоподъемность которых настолько велика, что рассчитывать долговечность уже не требуется.
Так как эти подшипники не участвуют в колебательных движениях, достаточно применения сферических роликоподшипников стандартного исполнения.
|
|
Пример:
Вес короба виброгрохота G = 60 кН Эксцентриковый радиус r = 0,005 м Частота вращения n = 850 мин-1
Число подшипников z = 2
Внутренние подшипники: нагрузка на подшипник определяется по формуле (1)
Эквивалентная динамическая нагрузка на подшипник для определения необходимой грузоподъемности подшипника P = 1,2 • 121 = 145 кН
2.4 Номограмма для определения центробежной силы неуравновешенной массы или центробежной силы короба виброгрохота
Fmax, Fmin и F – центробежные силы
n – частота вращения [мин-1]
r – радиус вибраций [м]
R – расстояние от центра тяжести вибровозбудителя до оси подшипника
b – ускорение [м/с2]
G – вес короба виброгрохота [кН]
G1 – вес вибровозбудителя [кН]
g = 9,81 – ускорение свободного падения [м/с2]
2.
 5 Номограмма для определения динамической грузоподъeмности
5 Номограмма для определения динамической грузоподъeмности
Для определения динамической грузоподъемности C [кН] необходимо знать следующие величины:
n – частота вращения [мин-1]
Lh – долговечность [ч]
P – динамическая эквивалентная нагрузка [кН]
Для вибровозбудителей с круговыми колебаниями и для внутренних подшипников в эксцентриковых виброгрохотах:
Для вибровозбудителей с круговыми колебаниями и для внутренних подшипников в эксцентриковых виброгрохотах:
где 1, 2 запас надежности
z – число подшипников
F – центробежная сила, найденная по номограмме 1 (раздел 2.4)
|
|
Эквивалентная динамическая нагрузка | Арболит
Нагрузки на подшипники редукторных узлов трансмиссии автомобилей обусловлены усилиями в зубчатых зацеплениях. Подшипники осей сателлитов планетарных передач дополнительно нагружаются центробежной силой от массы сателлитов.
В формулах для определения радиального и осевого усилий гипоидных и конических зубчатых колес с непрямыми зубьями верхние знаки следует принимать в случае, когда направление вращения (если смотреть на зубчатое колесо с вершины делительного конуса) совпадает с направлением наклона зубьев для ведущего зубчатого колеса, а для ведомого не совпадает; в про-
Осевая нагрузка на радиально-упорные однорядные подшипники при их парной установке на валу определяется исходя из внешней осевой нагрузки, обусловленной осевыми усилиями в зубчатых зацеплениях, и осевых сил и возникающих в опорах и от радиальных нагрузок. Номером следует обозначать ту опору, для которой направление действия осевой силы совпадает с направлением внешней осевой нагрузки, а номером — ту опору, для которой направления действия указанных сил не совпадают. А если нужен гусеничный экскаватор в спб то мы подскажем где можно его заказать на длительную аренду и с доставкой.
Номером следует обозначать ту опору, для которой направление действия осевой силы совпадает с направлением внешней осевой нагрузки, а номером — ту опору, для которой направления действия указанных сил не совпадают. А если нужен гусеничный экскаватор в спб то мы подскажем где можно его заказать на длительную аренду и с доставкой.
Определение радиальных и осевых нагрузок на подшипники начинают с расчета усилий в зубчатых зацеплениях и составления расчетной схемы. Далее находят радиальную и внешнюю осевую нагрузки на подшипники, затем определяют осевые составляющие усилия от радиальной нагрузки и, наконец, осевую нагрузку.
Внутренние динамические нагрузки возникают в агрегатах трансмиссии вследствие неточности изготовления зубчатых колес. Внешние динамические нагрузки обусловлены колебательными процессами в машинном агрегате автомобиля.
Коэффициент внутренних динамических нагрузок зацеплении зубчатых колес из-за погрешности основных шагов возникает динамическая нагрузка, оказывающая воздействие на зубья и подшипники. Влияние динамической нагрузки в зацеплении на долговечность подшипника учитывается коэффициентом.
Влияние динамической нагрузки в зацеплении на долговечность подшипника учитывается коэффициентом.
Решение проблемы установки драйверов
Статическая нагрузка против. Динамическая нагрузка: Демистификация грузоподъемности поддонов
На складе знание разницы между динамической и статической нагрузкой может означать разницу между тем, чтобы подвергать опасности сотрудников и продукты и обеспечивать их безопасность. Самое простое определение статической нагрузки по сравнению с динамической нагрузкой состоит в том, что статические нагрузки не перемещаются, а динамические перемещаются. В контексте цепочки поставок статическая нагрузка относится к загруженному поддону на полу, а динамическая нагрузка — к загруженному поддону, перемещаемому вилочным погрузчиком, домкратом для поддонов или другим оборудованием.Поскольку поддон, как правило, должен быть как динамическим, так и статическим на разных этапах своего пути, крайне важно знать особенности каждой грузоподъемности используемого вами поддона.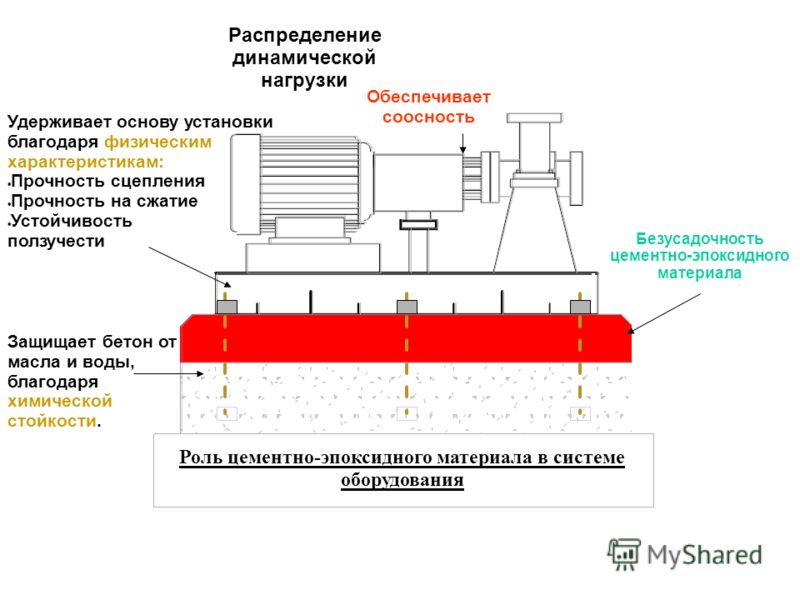 Различные материалы поддонов и конструкции поддонов имеют разные значения динамической и статической грузоподъемности. Понимание различий может помочь вам выбрать наилучший поддон для удовлетворения уникальных потребностей вашей цепочки поставок.
Различные материалы поддонов и конструкции поддонов имеют разные значения динамической и статической грузоподъемности. Понимание различий может помочь вам выбрать наилучший поддон для удовлетворения уникальных потребностей вашей цепочки поставок.
Статическая нагрузка по сравнению с. Динамическая нагрузка: основы
Каждый транспортировочный поддон будет иметь по крайней мере два разных максимального веса: статический и динамический.Риски несоблюдения максимальной нагрузки на поддоны высоки. Неисправный поддон может создать опасность на складе, которая может привести к травмам или гибели сотрудников. Вот почему очень важно понимать разницу между этими двумя показателями при определении максимальной нагрузки на поддон.
Номинальная статическая нагрузка
Это номинальная нагрузка на поддон, когда он не движется. Примером могут служить поддоны, на которых хранится запас на складском этаже. Это число сообщает персоналу склада, какой вес может выдержать поддон в одной стопке, так как нижний поддон будет нести основную нагрузку в штабеле из нескольких загруженных поддонов. Статическая грузоподъемность, как правило, выше, чем динамическая, поэтому может потребоваться разгрузка продуктов с поддона, чтобы привести его в соответствие с требованиями по весу для перемещения.
Статическая грузоподъемность, как правило, выше, чем динамическая, поэтому может потребоваться разгрузка продуктов с поддона, чтобы привести его в соответствие с требованиями по весу для перемещения.
Номинальная динамическая нагрузка
Динамическая грузоподъемность дает максимальную грузоподъемность перемещаемого поддона. Как правило, это означает, что поддон поднимается и переносится с помощью вилочного погрузчика, домкрата или крана-штабелера. Распределение нагрузки имеет жизненно важное значение, так как неравномерно распределенный вес может привести к опрокидыванию или переворачиванию поддона во время движения.
Номинальная грузоподъемность стеллажа Edge-Rack
Грузоподъемность боковой стеллажной системы означает, какой вес поддон может выдержать при хранении на системе стеллажей для поддонов. Поскольку складские стеллажи обычно включают в себя стеллажи, которые поддерживают поддоны только с двух сторон, вместимость стеллажей для поддонов обычно ниже, чем их статическая или динамическая грузоподъемность. Вместимость стеллажей также зависит от прочности самих складских стеллажей, что часто является ограничивающим фактором.
Вместимость стеллажей также зависит от прочности самих складских стеллажей, что часто является ограничивающим фактором.
Динамическая грузоподъемность поддона обычно представляет собой лишь часть статической нагрузки.
В большинстве случаев грузоподъемность статического веса поддона намного превышает его динамическую грузоподъемность или грузоподъемность стеллажа. Это связано с тем, что при статической нагрузке сила нагрузки на платформу остается постоянной. При динамической нагрузке она может резко меняться во время ускорения или замедления, или вес может перемещаться из одной области в другую. Подъемники для поддонов и вилочные погрузчики также оказывают концентрированное давление на поддоны, а не равномерно поддерживают вес загруженного поддона. В результате динамическая грузоподъемность поддона обычно представляет собой лишь часть статической оценки.
Выбор поддонов, выдерживающих нагрузку при любых условиях
Грузоподъемность поддона определяется его основным материалом и базовой конструкцией. Поскольку многие из этих конструкций стандартизированы, их динамическая и статическая грузоподъемность относительно постоянна и предсказуема.
Поскольку многие из этих конструкций стандартизированы, их динамическая и статическая грузоподъемность относительно постоянна и предсказуема.
Тип поддона | Статический рейтинг | Динамический рейтинг |
| Деревянный стрингер : Обычно это самые дешевые поддоны для коммерческого использования.В этих поддонах используются доски с надрезами или «стрингеры» для поддержки верхних и нижних досок настила. | 2500 фунтов | 2500 фунтов |
| Деревянный блок: Поддоны из блоков более долговечны, чем стрингеры, поскольку они изготовлены из более прочных досок и деревянных блоков. Эта повышенная стабильность также увеличивает их грузоподъемность. | 5500 фунтов | 4600 фунтов |
Пластик: Высококачественный пластиковый поддон обычно весит менее 50 фунтов. Поскольку он отлит в форму, а не скреплен вместе, в нем нет винтов или другого оборудования, и каждый поддон един с каждым другим поддоном. Поскольку он отлит в форму, а не скреплен вместе, в нем нет винтов или другого оборудования, и каждый поддон един с каждым другим поддоном. | 30 000 фунтов | 5000 фунтов |
Многие факторы могут влиять на динамическую и статическую грузоподъемность поддона. Это включает в себя возраст поддона, тип используемой древесины (в случае деревянных поддонов) и наличие у них каких-либо повреждений или ремонтов. В идеале лучше округлять вес при загрузке поддонов, чтобы ограничить риск их перегрузки.
Пластиковые поддоны обычно обладают динамической способностью, превышающей динамическую нагрузку их деревянных аналогов.
Сравнивая статическую и динамическую нагрузки различных материалов и типов поддонов, становится ясно, что поддоны из высококачественного пластика являются самыми прочными. Высокая статическая грузоподъемность делает пластиковые поддоны отличным выбором для хранения продукции на складе. Поскольку пластиковые поддоны также обычно обладают динамической способностью, превышающей динамическую способность их деревянных аналогов, загруженные пластиковые поддоны можно перемещать без предварительного снятия продуктов с поддона. Большая прочность и долговечность пластиковых поддонов в конечном итоге снижает вероятность повреждения продукта в результате отказа поддона, что экономит деньги и время предприятий в долгосрочной перспективе.
Большая прочность и долговечность пластиковых поддонов в конечном итоге снижает вероятность повреждения продукта в результате отказа поддона, что экономит деньги и время предприятий в долгосрочной перспективе.
Аренда Пластиковые поддоны iGPS — это разумный способ максимально увеличить пространство для хранения, а также обеспечить безопасное и простое обращение с поддонами. Их статическая и динамическая грузоподъемность была проверена во многих различных условиях, поэтому вы можете быть уверены, что получаете одну из самых надежных платформ на рынке.Для получения дополнительной информации, свяжитесь с нами на 1-800-884-0225, по электронной почте специалист по [Email Protected] или посещение наших .
Отклонение статической и динамической нагрузки
Введение
В первую очередь резина используется вместо металлических, керамических и других жестких материалов, потому что она обеспечивает большее отклонение при заданной силе, чем эти другие материалы.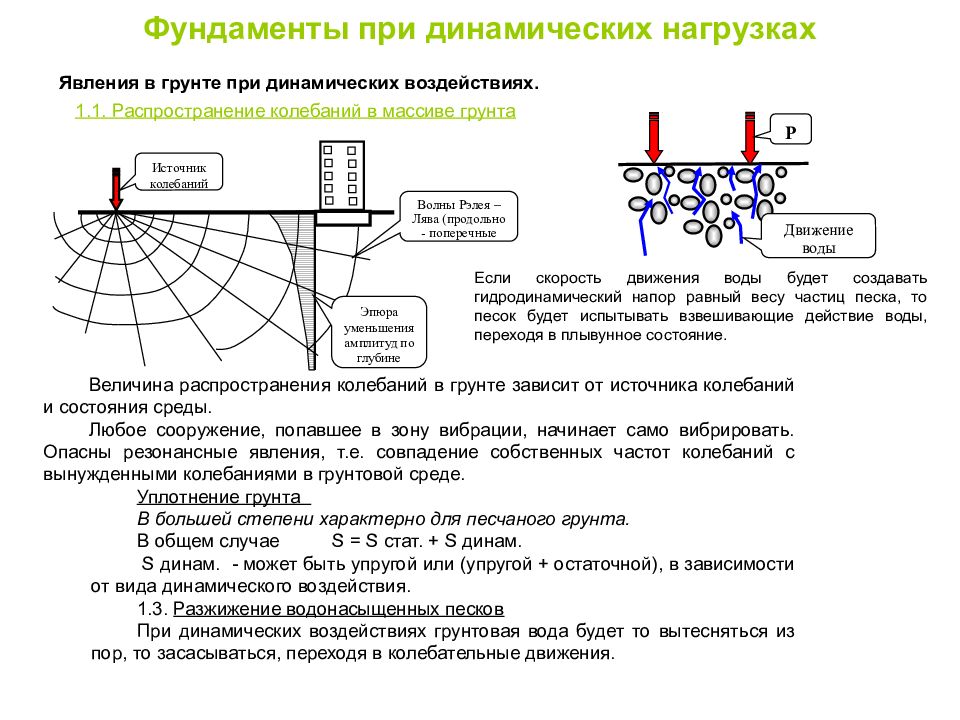 Большинство применений каучука основано на этой характеристике.
Большинство применений каучука основано на этой характеристике.
Во многих случаях применения резины изменение жесткости не имеет решающего значения для функционирования резинового изделия, и в таких случаях достаточно значения твердости по Шору А.
Резина используется в качестве конструкционного материала в упругих опорах, виброизоляторах, демпферах, ударных подушках и во многих других подобных устройствах. Если характеристики статической или динамической жесткости становятся критически важными для функционирования продукта, должны быть установлены соответствующие спецификации испытаний.
Статические методы
Если для изделия установлены характеристики статической нагрузки-прогиба, в дополнение к требованиям к твердости, характеристики нагрузки-прогиба должны превалировать над твердостью, должны быть указаны на чертеже изделия и согласованы между потребителем и изготовителем резины. Статическое испытание является «статическим» только в том смысле, что приложение нагрузки останавливается до проведения измерения или скорость отклонения обычно не превышает 0,8 мм/с (2 дюйма/мин). Такое испытание обычно подвергает резину сдвигу или сжатию.Существует несколько способов задания характеристик статической нагрузки-прогиба:
Такое испытание обычно подвергает резину сдвигу или сжатию.Существует несколько способов задания характеристик статической нагрузки-прогиба:
- Укажите жесткость пружины в нагрузке на единицу прогиба, например, Нм (фунт/дюйм) или крутящий момент на радиан, например, Нм/рад (фунт-дюйм/рад).
- Укажите нагрузку для отклонения продукта в пределах заданного диапазона отклонения.
- Укажите отклонение, приводящее к нагрузке в пределах указанного диапазона нагрузки.
Динамические методы
Применение резины в качестве виброизолятора зависит от поведения резины в динамических условиях эксплуатации.Резина
в динамике жестче, чем в статике; и, поскольку отношение статической жесткости к динамической жесткости варьируется в зависимости от отдельных составов, может быть целесообразным указать динамические характеристики резины для таких применений.
Если указана динамическая жесткость или жесткость пружины, и они имеют решающее значение для характеристик резинового изделия, между заказчиком и производителем резины должны быть установлены полные условия и методы измерения.
Существует несколько методов динамического тестирования:
- Стационарный резонанс
- Резонанс свободного распада
- Установившееся состояние, нерезонансный
- Оценка отскока
Возраст
Старение резиновых смесей во времени представляет собой сложный процесс.Нормальным чистым эффектом старения является увеличение модуля или жесткости. Величина этого изменения зависит от конкретного материала и условий окружающей среды.
Кратковременный возраст в смысле минимального количества часов, которое должно пройти между формовкой и оценкой, также является важным фактором. В зависимости от характера продукта минимальный срок варьируется от 24 до 168 часов.
Динамическая история
На характеристики нагрузки-прогиба резинового изделия влияет история эксплуатации этого конкретного изделия.Начальный цикл нагружения новой детали или детали, находившейся в статическом состоянии в течение определенного периода времени, указывает на более жесткую характеристику нагрузки-прогиба, чем последующие циклы. При статических испытаниях этот эффект стабилизируется, и характеристики нагрузки-прогиба обычно становятся повторяемыми после двух-четырех циклов кондиционирования.
При статических испытаниях этот эффект стабилизируется, и характеристики нагрузки-прогиба обычно становятся повторяемыми после двух-четырех циклов кондиционирования.
При динамических испытаниях период кондиционирования обычно выбирается как время, необходимое для получения воспроизводимых результатов.
Температура
Температура влияет на жесткость пружины: чем выше температура, тем ниже жесткость пружины, а чем ниже температура, тем выше жесткость пружины резинового изделия, не находящегося под постоянным натяжением.
Условия испытаний
Следующие детали должны быть определены на чертеже изделия или в указанной спецификации, чтобы обеспечить уместную и непротиворечивую оценку характеристик изделия:
- Режим испытаний
- Растяжение, сдвиг или сжатие. Крайне желательна схематическая диаграмма, изображающая ориентацию продукта. Жесткость пружины в режиме сжатия всегда выше, чем жесткость пружины в режиме сдвига.
- Статическая или динамическая
- Динамическая жесткость пружины всегда выше, чем статическая.

- Тестовый уровень и режим управления
- Должны быть указаны уровень статической испытательной нагрузки или уровень деформации вместе с соответствующими пределами прогиба или пределами нагрузки в ответ на деформацию.
- Уровни динамической нагрузки должны обозначаться плюсовым (+) значением для направленных вниз сил и отрицательным (-) значением для восходящих сил. Динамические испытания с использованием контроля деформации должны быть определены двойными значениями амплитуды (полной амплитуды).
- Величина и направление предварительного натяга, если требуется.
- Линейная или угловая скорость нагрузки или циклическая частота.
- Характер и количество или продолжительность циклов кондиционирования, необходимых перед циклом испытаний или периодом испытаний.
- Температура окружающей среды при испытании и период времени, в течение которого изделие выдерживается при температуре испытания перед оценкой.

- Когда требования указаны как «Коэффициент упругости», необходимо указать место на диаграмме отклонения нагрузки, в котором проводится касательная, или уровни нагрузки, между которыми берется среднее значение.
Когда это применимо, инженер-конструктор должен указать нагрузку-прогиб, жесткость пружины, метод испытаний и допуски на нагрузку-прогиб. В таблице 10 представлены стандарты для трех обозначений на чертежах допусков нагрузки-прогиба. Если характеристики демпфирования требуются как часть динамической спецификации, коммерческие допуски будут составлять ±25% для деталей с твердостью до 65 единиц по дюрометру (SHORE A) и ±30% для деталей с твердостью выше 65 единиц по дюрометру (SHORE A).
Таблица 10
ОБОЗНАЧЕНИЕ НА ЧЕРТЕЖЕ RMA ДЛЯ ДОПУСТИМОЙ НАГРУЗКИ-ПРОГИБА
| Назначение чертежа | Твердость по дюрометру | Допустимый диапазон толщины резиновой стенки 6 мм (0.25 дюймов) или более | Допустимый диапазон толщины резиновой стенки менее 6 мм (0,25 дюйма) | |
| Д1 | Твердость по дюрометру 65 (Шор A) или ниже | ±10% | ±15% | Очень высокая точность. Такой жесткий допуск следует запрашивать только в необычных обстоятельствах. Такой жесткий допуск следует запрашивать только в необычных обстоятельствах. |
| Твердость выше 65 по дюрометру (Шор A) | ±15% | ±20% | ||
| Д2 | Твердость по дюрометру 65 (Шор A) или ниже | от ±11 % до ±14 % | от ±16 % до ±20 % | Точность |
| Твердость выше 65 по дюрометру (Шор А) | от ±16 % до ±19 % | от ±21% до ±26% | ||
| Д3 | Твердость по дюрометру 65 (Шор A) или ниже | ±15% | ±20% | Коммерческий |
| Твердость выше 65 по дюрометру (Шор A) | ±20% | ±25% |
В чем разница между статическими и динамическими нагрузками?
Статические нагрузки отличаются от динамических тем, что сила статической нагрузки остается постоянной. При динамической нагрузке силы, связанные с нагрузкой, изменяются в зависимости от внешних обстоятельств.
При динамической нагрузке силы, связанные с нагрузкой, изменяются в зависимости от внешних обстоятельств.
Статическая нагрузка и динамическая нагрузка
Основное различие между статической и динамической нагрузкой заключается в силе, создаваемой весом объекта. В статике нагрузка остается постоянной и не меняется со временем. При динамической нагрузке какой-то внешний фактор вызывает изменение сил веса груза. Некоторые из факторов, которые могут повлиять на нагрузку и сделать ее динамической, включают:
 В результате большая нагрузка оказывает большее влияние на меньшую нагрузку, возможно, даже приводя к ее дисбалансу.
В результате большая нагрузка оказывает большее влияние на меньшую нагрузку, возможно, даже приводя к ее дисбалансу.Примеры статической и динамической нагрузки
Хорошим примером статической нагрузки является грузовик с грузом внутри, неподвижно стоящий на одном месте. Сила веса груза имеет мало шансов измениться, пока грузовик остается неподвижным. Как только грузовик начинает двигаться, груз становится динамическим, так как сила движения может вызвать смещение груза, изменяя действие силы веса груза.Если грузовик движется слишком быстро, это может даже вызвать сильное смещение сил груза, что приведет к его падению или, по крайней мере, затруднит управление грузовиком по дорожному покрытию. Кроме того, при остановке сила веса груза может смещаться вперед, что затрудняет быструю остановку транспортного средства.
Кроме того, при остановке сила веса груза может смещаться вперед, что затрудняет быструю остановку транспортного средства.
Мост представляет собой еще один пример действия статических и динамических сил. Вес моста является статической нагрузкой, так как он не меняется со временем, пока по нему ничего не движется или внешние силы, такие как ветер, не движутся против него.Грузовик, движущийся по мосту, создает динамическую нагрузку на мост, увеличивая вес моста по мере его пересечения. Ветер, дующий на мост, также может изменять силы веса моста, так как перемещает его из стороны в сторону, создавая динамическую нагрузку на мост. Вот почему важно, чтобы инженеры учитывали все силы, которые могут воздействовать на конкретный мост, чтобы спроектировать устойчивую и безопасную конструкцию. Еще одна важная сила, о которой следует помнить, — это кручение: любое скручивание моста на ветру вызывает дополнительное напряжение конструкции, что, в свою очередь, может повлиять на то, какую нагрузку мост может выдержать.
БОЛЬШЕ ОТ REFERENCE.COM
Произошла ошибка при настройке пользовательского файла cookie
Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка браузера для приема файлов cookie
Существует множество причин, по которым файл cookie не может быть установлен правильно. Ниже приведены наиболее распространенные причины:
- В вашем браузере отключены файлы cookie.Вам необходимо сбросить настройки браузера, чтобы принять файлы cookie, или спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает, хотите ли вы принимать файлы cookie, и вы отказались.
Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файл cookie. - Ваш браузер не поддерживает файлы cookie. Попробуйте другой браузер, если вы подозреваете это.

- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г.,
браузер автоматически забудет файл cookie.Чтобы это исправить, установите правильное время и дату на своем компьютере. - Вы установили приложение, которое отслеживает или блокирует установку файлов cookie.
Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Предоставить доступ без файлов cookie
потребует от сайта создания нового сеанса для каждой посещаемой вами страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в файле cookie; никакая другая информация не фиксируется.
Как правило, в файле cookie может храниться только та информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт
не может определить ваше имя электронной почты, если вы не решите ввести его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступ к
остальной части вашего компьютера, и только сайт, создавший файл cookie, может его прочитать.
Расчетные коэффициенты для динамических нагрузок
Что такое динамические нагрузки?
Проще говоря, динамическая нагрузка — это любая нагрузка, которая перемещается, изменяя величину или направление во времени. Нагрузки в статической системе постоянны и неизменны. Законы движения Ньютона легко согласовывают равновесие в статических системах.
Для целей этой статьи следует учитывать, что термин «динамическая нагрузка» относится к любой нагрузке в движении, изменяющей скорость или направление. Ударные нагрузки, ударные нагрузки и вибрационные нагрузки можно считать динамическими по своей природе, но это не одно и то же.
Основы.
Одно из самых основных уравнений в физике: F=ma . Сила равна произведению массы на ускорение. В этом уравнении любое изменение значений массы или ускорения приводит к пропорциональному изменению силы. Компонент ускорения в этом уравнении подразумевает, что время является связанным фактором; действительно, ускорение — это скорость изменения скорости во времени. Когда объект ускоряется или замедляется, важно изменение его скорости во времени, но F=ma учитывает только мгновенную силу инерционной массы объекта по отношению к скорости его изменения во времени при ускорении с фиксированной скоростью.Упрощенно, если объект ускоряется, то к нему приложена сила. С другой стороны, если объект не ускоряется (ни в состоянии покоя, ни с постоянной скоростью), то на него не действует никакая сила. Это основные положения других формул, которые рассчитывают кинетическую энергию, силу удара и рассеивание энергии.
Самое время.
Мы склонны думать о динамических нагрузках с точки зрения падающего объекта, потому что относительно легко связать ускорение «a» , в F = ma , как силу тяжести. Однако если направление движения не является вертикальным, то мы можем не полностью учитывать динамические нагрузки надлежащим образом, главным образом потому, что гравитация менее интуитивно понятна, когда движение не является вертикальным или направленным вниз.
Однако если направление движения не является вертикальным, то мы можем не полностью учитывать динамические нагрузки надлежащим образом, главным образом потому, что гравитация менее интуитивно понятна, когда движение не является вертикальным или направленным вниз.
Важнее не то, что объект меняет направление или останавливается, а то, как быстро он это делает. Важно не падение, а внезапная остановка в конце. Время решает все: если я могу остановить свое падающее тело за менее внезапный промежуток времени в несколько секунд, то остановка в конце становится менее критической и, безусловно, менее грязной.Удержите эту мысль…
E k =1/2mv 2 — простая формула кинетической энергии. Кинетическая энергия измеряется в джоулях — это работа, затрачиваемая на приложение силы в 1 ньютон (или 1 кг·м/сек 2 ) на расстояние 1 метр. Ньютон (Н) — это сила тяжести, действующая на объект массой (м). Если я вешу 100 кг и этот вес является произведением моей массы на силу тяжести, то моя масса равна 10,2 кг, и с помощью силы тяжести я развиваю силу, равную 10. 2 кг x 9,8 м/сек2 = 10,2*9,8 кг·м/сек2 = 100 Н на поверхности земли. F=ма .
2 кг x 9,8 м/сек2 = 10,2*9,8 кг·м/сек2 = 100 Н на поверхности земли. F=ма .
Аналогичным образом это можно выразить через импульс (P) = масса (m) x скорость при ударе (v), поэтому P = 10,2 Н (4,4 м/сек) = 44,9 кг·м/сек в данный момент времени. Импульс не является силой сам по себе; это произведение, но оно может быть связано со вторым законом Ньютона и, следовательно, с инерцией. В этом уравнении масса (m) относится к инерционной массе или коэффициенту пропорциональности относительно тенденции объекта сопротивляться изменениям в движении.Куда мы катимся со всем этим?
Вернемся к примеру с моим падающим телом: думайте о ударе с точки зрения того, что останавливает мое падение. Если я столкнусь с подушкой безопасности, назовите это трюком; если я попаду на бетонный тротуар, назовите это грязным. Интуитивно это должно выражаться в том, сколько времени требуется для остановки — как быстро поглощается или рассеивается кинетическая энергия. Теперь мы чего-то достигли, и это обо мне!
Теперь мы чего-то достигли, и это обо мне!
Время перемен.
Законы Ньютона предполагают, что любое изменение направления является результатом действия силы, имеющей достаточную величину, чтобы вызвать такое изменение.При проектировании системы, рассчитанной на любую нагрузку, мы должны учитывать конструктивный фактор, чтобы объект, подвергающийся воздействию, был достаточно прочным, чтобы он не вышел из строя или не сломался при воздействии противодействующей силы. Проще говоря, это остановка объекта во время его движения. Подумайте об этом на мгновение — американские горки на извилистой дорожке, Питер Пэн на конце провода — для движения требуется сила, а для изменения направления или остановки требуется противодействующая сила.
В случае американских горок автомобиль должен быть сконструирован таким образом, чтобы изменение направления, вызванное контактом колес с дорожкой, не приводило к смещению или поломке колес.То же самое и в случае человека на проводе. Силы, прилагаемые для остановки движения, должны учитывать не только компонентную прочность материалов, используемых в системе, но также должны учитывать максимальные силы, выдерживаемые человеческим телом без повреждений. Когда система сил не рассматривается должным образом, результаты могут быть смертельными. Проще говоря, если автомобиль с американскими горками или человек слишком быстро меняют направление, реакции инерционных сил могут быть значительными. Если изменение вектора сил постепенное, динамические нагрузки значительно уменьшаются.
Силы, прилагаемые для остановки движения, должны учитывать не только компонентную прочность материалов, используемых в системе, но также должны учитывать максимальные силы, выдерживаемые человеческим телом без повреждений. Когда система сил не рассматривается должным образом, результаты могут быть смертельными. Проще говоря, если автомобиль с американскими горками или человек слишком быстро меняют направление, реакции инерционных сил могут быть значительными. Если изменение вектора сил постепенное, динамические нагрузки значительно уменьшаются.
Обрешетка для труб.
Начнем с напоминания о том, как работает система противовесов с ручным управлением:
Нагрузка на обрешетку уравновешивается противовесом вала, в идеале идеально сбалансированным, но обычно в пределах 50 фунтов равновесия при нормальных условиях эксплуатации.
Когда рабочий трос на этом теоретически сбалансированном наборе тросов тянется оператором, вызывая движение вала вверх или вниз, возникает связанная с этим реакция канатных подъемных тросов на обрешетку, поэтому она перемещается вверх или вниз. Сила для начала движения обычно очень постепенная, так же как и сила для остановки движения (постепенная за счет растушевки рабочей линии, предположительно руками в перчатках). Это ручное действие по своей сути обеспечивает небольшой фактор безопасности, потому что количество трения, которое может быть применено руками в перчатках, напрямую связано со способностью противостоять теплу, выделяемому таким трением. Все это возможно, потому что нагрузку динамического движения или дисбаланса в системе можно контролировать за счет трения, создаваемого рукой человека в перчатке, и возвращать ее почти к равновесию с небольшими усилиями.
Сила для начала движения обычно очень постепенная, так же как и сила для остановки движения (постепенная за счет растушевки рабочей линии, предположительно руками в перчатках). Это ручное действие по своей сути обеспечивает небольшой фактор безопасности, потому что количество трения, которое может быть применено руками в перчатках, напрямую связано со способностью противостоять теплу, выделяемому таким трением. Все это возможно, потому что нагрузку динамического движения или дисбаланса в системе можно контролировать за счет трения, создаваемого рукой человека в перчатке, и возвращать ее почти к равновесию с небольшими усилиями.
С другой стороны (без каламбура), если дисбаланс нагрузки больше, чем может выдержать человеческая рука, и больше, чем может противостоять рабочее трение, тогда силы остаются неуравновешенными, и движение продолжается до тех пор, пока что-то не действует с противодействующей силой на все, что движется. В одном примере, который почти никогда не случается, противовес снимается с вала, когда обрешетка находится в высоком положении, и устраняется трение, вызванное замком веревки или «дядей-приятелем». Происходит дисбаланс нагрузки, равновесие нарушается и движение становится неизбежным.Согласно законам Ньютона, чтобы остановить это движение, нам нужна равная и противодействующая сила. В данном случае упоры на валу (также ласково называемые краш-барами) устанавливают конечный, в некоторой степени эффективный предел движения.
Происходит дисбаланс нагрузки, равновесие нарушается и движение становится неизбежным.Согласно законам Ньютона, чтобы остановить это движение, нам нужна равная и противодействующая сила. В данном случае упоры на валу (также ласково называемые краш-барами) устанавливают конечный, в некоторой степени эффективный предел движения.
Поверь мне: сбежавшая беседка не любит работать в рамках. За секунду-две и при достаточном адреналине оператор может достаточно быстро отпрыгнуть, инстинктивно приняв извечную выразительную позу, означающую только одно: «Я этого не делал, клянусь!» Доли секунды спустя сбежавшая ось решает, что ей все еще не нравится работать в определенных пределах, — она нажимает на упор, который пытается сопротивляться с такой же противодействующей силой, в результате чего обычно что-то ломается.Шокирующе, я знаю.
Есть несколько факторов, которые способствуют этому небольшому беспорядку: площадь удара очень сконцентрирована, сила удара распределяется между очень небольшим количеством компонентов, материалы, используемые для упоров, как правило, совсем не упругие (стальные уголки, бамперы из твердой древесины и действительно большие болты), а время торможения и остановки, необходимое для достижения требуемого равновесия сил, чрезвычайно мало.
Кто-то мог указать расчетный коэффициент 5:1 для стали в этой системе, но это, вероятно, применялось только к нормальным расчетным нагрузкам, возникающим при нормальных условиях эксплуатации.Он не учитывал и не должен учитывать случайные нагрузки, такие как падение полностью нагруженной латы с высокой отделки.
Назад, откуда мы начали.
Эти же принципы применяются при выборе тормоза для моторизованной подъемной системы. Если груз представляет собой структурную раму, рама должна быть спроектирована таким образом, чтобы выдерживать ее остановку в любое время, требуемое расчетным временем активации тормоза. Исследуя динамометрические образцы динамических тестов на тормозную силу, мы увидели, что коэффициенты ударной нагрузки из-за торможения варьируются от 1.от 5 до почти 4, в зависимости от нагрузки и времени реакции тормозного соленоида.
В моторизованных системах, используемых для полетов артистов, эти динамические нагрузки (из-за торможения и изменения направления) могут стать критическими для безопасности артистов. В системе защиты от падения максимальное удерживающее усилие, которое разрешено передавать на человека с привязью, не должно превышать 1800 фунтов. Учтите, что человек весом 200 фунтов, падающий с высоты 4 фута на самоубирающуюся линию жизни с тормозным путем, равным 2, и без амортизатора создает тормозную силу около 4800 фунтов, и это все еще грязно!
В системе защиты от падения максимальное удерживающее усилие, которое разрешено передавать на человека с привязью, не должно превышать 1800 фунтов. Учтите, что человек весом 200 фунтов, падающий с высоты 4 фута на самоубирающуюся линию жизни с тормозным путем, равным 2, и без амортизатора создает тормозную силу около 4800 фунтов, и это все еще грязно!
Понятия динамических нагрузок, инерционной массы, скорости изменения скорости во времени — все они уходят корнями в F=ma .Помните, что это должно быть очень упрощенным обсуждением динамических нагрузок, надеюсь, достаточно, чтобы возбудить ваш аппетит. Не пытайтесь повторить это дома, друзья!
Реализовать трехфазную динамическую нагрузку с активной мощностью и
реактивная мощность как функция напряжения или управляемая от внешнего
вход
Описание
Блок Three-Phase Dynamic Load реализует трехфазную трехпроводную динамическую нагрузку.
нагрузка, у которой активная мощность P и реактивная мощность Q изменяются в зависимости от напряжения прямой последовательности. Токи обратной и нулевой последовательности не моделируются. Таким образом, три тока нагрузки равны
Токи обратной и нулевой последовательности не моделируются. Таким образом, три тока нагрузки равны
сбалансированный, даже в условиях несбалансированного напряжения нагрузки.
Полное сопротивление нагрузки поддерживается постоянным, если напряжение на клеммах
V нагрузки ниже заданного значения Vmin. Когда терминал
напряжение больше, чем значение Vmin, активная мощность P и реактивная
мощность Q нагрузки изменяется следующим образом:
P(s)=P0(VV0)np1+Tp1s1+Tp2sQ(s)=Q0(VV0)nq1+Tq1s1+Tq2s,
где
В 9036 0 это
начальное напряжение прямой последовательности.P 0 и Q или
начальные активная и реактивная мощности при начальном напряжении В o .В — напряжение прямой последовательности.
n p и n q
показатели (обычно от 1 до 3), контролирующие характер
нагрузка.T p 1 и T p 2
постоянные времени, управляющие динамикой активной мощности P .
T q 1 и T q 2
постоянные времени, управляющие динамикой реактивной мощности Q .
Для нагрузки постоянного тока, например, вы устанавливаете n p на
1 и n q к 1, а для постоянных
импеданс нагрузки, который вы установили n p на
2 и n q до 2.
Входы и выходы
Если Внешнее управление PQ
выбран, появляется вход Simulink, помеченный PQ .Этот вход используется для управления активной и реактивной мощностью
нагрузка от вектора двух сигналов [P, Q].
Результат м представляет собой вектор, содержащий следующие
три сигнала:
Динамическая нагрузка на исходном уровне может предсказать рентгенографическое прогрессирование заболевания при остеоартрите медиального отдела коленного сустава
Цель:
Проверить гипотезу о том, что динамическая нагрузка на исходном уровне может предсказать рентгенографическое прогрессирование заболевания у пациентов с медиальным остеоартритом коленного сустава (ОА).
Методы:
В течение 1991-93 гг. были собраны исходные данные путем оценки боли, рентгенографии и анализа походки у 106 пациентов, направленных в больницу с медиальным ОА коленного сустава. Через шесть лет наблюдения 74 пациента были повторно обследованы для оценки рентгенологических изменений. Рентгенологически прогрессирование заболевания определяли как сужение минимальной суставной щели медиального отдела более чем на одну степень.
Результаты:
У 32 пациентов с прогрессированием заболевания боль была более сильной, а момент приведения был выше в начале исследования, чем у пациентов без прогрессирования заболевания (n=42). Сужение медиального отдела суставной щели в течение шестилетнего периода значимо коррелировало с моментом приведения при входе. Момент приведения значительно коррелировал с механической осью (варусное выравнивание) и отрицательно с шириной суставной щели и оценкой боли.Логистический регрессионный анализ показал, что риск прогрессирования ОА коленного сустава увеличился в 6,46 раза при увеличении момента приведения на 1%.
Момент приведения значительно коррелировал с механической осью (варусное выравнивание) и отрицательно с шириной суставной щели и оценкой боли.Логистический регрессионный анализ показал, что риск прогрессирования ОА коленного сустава увеличился в 6,46 раза при увеличении момента приведения на 1%.
Выводы:
Результаты показывают, что исходный момент приведения коленного сустава, отражающий динамическую нагрузку на медиальный отдел, может предсказать рентгенографическое прогрессирование ОА в течение шести лет наблюдения за пациентами с медиальным ОА коленного сустава.
.


 Специальные подшипники FAG, разработанные для вибрационных машин, наилучшим образом подтвердили свою состоятельность на практике.
Специальные подшипники FAG, разработанные для вибрационных машин, наилучшим образом подтвердили свою состоятельность на практике.



