Формула для расчета площади: Формулы площади. Площадь треугольника, квадрата, прямоугольника, ромба, параллелограмма, трапеции, круга, эллипса.
- Формулы площадей 📐 всех фигур
- Площадь треугольника
- Прямоугольного
- Равностороннего треугольника
- Площадь равнобедренного прямоугольного треугольника
- Площадь треугольника через синус
- Площадь треугольника через косинус
- Площадь треугольника через радиус описанной окружности
- Произвольного треугольника
- Площадь треугольника через высоту
- Площадь треугольника через полупериметр
- Площадь тупоугольного треугольника
- Площадь треугольника через радиус вписанной окружности
- Площадь параллелограмма
- Формула площади прямоугольника
- Площадь квадрата
- Площадь четырехугольника
- Площадь многоугольника
- Площадь ромба
- Площадь многогранника
- Площадь пятиугольника
- Площадь закрашенного сектора
- Площадь круга
- Площадь трапеции
- Площадь треугольника
- Формулы геометрии. Площади фигур — материалы для подготовки к ЕГЭ и ОГЭ по Математике
- Площади фигур
- Площади многоугольников
- Формулы площади
- Формулы площади поверхности
- Что такое площадь?
- Формула площади и объема для геометрических фигур
- Список всех площадей Формулы
- Площадь четырехугольной призмы, объем
- Объем капсулы, площадь, окружность
- Объем, площадь поверхности и высота конической усадки
- Объем цилиндрической трубы
- Соотношение сторон и пиксели
- Объем Barell
- Преобразование прямоугольного в полярное
- Объем цилиндра с полусферическими концами
- Апофема правильного многоугольника
- Объем восьмиугольной пирамиды
- Cicumcircle правильного многоугольника
- Окружность правильного многоугольника
- Правильный многоугольник
- Площадь восьмиугольной призмы, объем, площадь поверхности
- Площадь сектора круга
- Площадь трапеции
- Площадь и периметр стадиона
- Объем полого цилиндра, площадь, площадь поверхности, окружность
- Объем аквариума
- Объем трубы
- Длина хорды окружности
- Длина дуги окружности
- Площадь поверхности прямоугольной призмы, объем
- Градус Измерение сектора
- Площадь кольцевого пространства
- LSA квадратной пирамиды
- Диагональ прямоугольника
- Общая площадь прямоугольного правого клина
- Площадь полукруга
- Площадь и периметр масштабного треугольника
- Площадь правильного шестиугольника
- Центральный угол окружности
- Внешние углы выпуклого многоугольника
- Площадь эллипса
- Градиент линии на плоскости
- Площадь сегмента круга
- Радиус вписанной окружности в октаэдре
- Радиус описанной окружности в октаэдре
- Площадь поверхности октаэдра
- Объем октаэдра
- Радиус вписанной окружности в Dod ecahedron
- Площадь a Сегмент окружности
- Боковая площадь наклонной призмы
- Объем наклонной призмы
- Наклонная высота правильной пирамиды
- Площадь боковой поверхности правильной пирамиды с использованием полупериметра
- Площадь боковой поверхности правильной пирамиды с использованием основания и бокового края
- Площадь правильного шестиугольника
- Высота правильной пирамиды
- Площадь боковой поверхности правильной пирамиды
- Общая площадь поверхности регулярной Пирамида
- Объем правильной пирамиды на основе площади основания
- Радиус вписанной окружности
- сегмент длины хорды окружности
- Высота сегмента круга
- Сегмент периметра круга
- Сегмент площади круга
- Общая площадь поверхности наклонной призмы
- Длина дуги Стрелец
- Внутренние углы выпуклости Многоугольник
- Наклонная высота пирамиды
- Наклонная высота квадратной пирамиды
- Высота треугольника шкалы
- Площадь вальмовой крыши
- Площадь трубы
- Площадь поверхности трубы
- Площадь боковой поверхности цилиндра
- Окружность круга
- Высота прямоугольной призмы
- Радиус окружности
- Длина дуги
- Окружность эллипса
- Периметр правого треугольника
- Площадь круга
- Калькулятор объема гиперсферы
- Площадь изогнутой поверхности (CSA) кубоида
- CSA цилиндра
- Додекагон
- Наклонная высота конуса
- Площадь поверхности конуса
- Площадь изогнутой поверхности конуса
- Объем конуса
- Диагональ прямоугольной призмы
- Площадь сегмента круга
- Апофема Пентагона
- Центроид параллелограмма
Формулы площадей 📐 всех фигур
Площадь треугольника
Прямоугольного
Равностороннего треугольника
Площадь равнобедренного прямоугольного треугольника
S = a2/2
Площадь треугольника через синус
Площадь треугольника через косинус
Для нахождения площади треугольника нужно знать все стороны. По теореме косинусов квадрат неизвестной стороны равен:
Следовательно:
Далее используем формулу Герона:
Площадь треугольника через радиус описанной окружности
Произвольного треугольника
Формула Герона
Площадь треугольника через высоту
Площадь треугольника через полупериметр
Формула Герона
является полупериметром.
Площадь тупоугольного треугольника
S = ah/2
Площадь треугольника через радиус вписанной окружности
S = p×r
где p — полупериметр:
Площадь параллелограмма
Через синус
Через стороны и углы
S = a×b×sin(α) = a×b×sin(β)
Через диагонали и угол между ними
Формула площади прямоугольника
S = a×b
Площадь квадрата
S = a2
Площадь четырехугольника
Выпуклого четырехугольника
где
Площадь многоугольника
S = S1 + S2 + S3 + S4
Правильного многоугольника
где n — количество сторон многоугольника.
Площадь ромба
Площадь многогранника
Площадь пятиугольника
Площадь закрашенного сектора
Площадь круга
S = πr2
Площадь трапеции
Через основания и высоту
Через высоту и среднюю линию
S = hm
Через четыре стороны
Через диагонали и угол между ними
Через основания и два угла
Формулы геометрии. Площади фигур — материалы для подготовки к ЕГЭ и ОГЭ по Математике
Чтобы решить задачи по геометрии, надо знать формулы — такие, как площадь треугольника или площадь параллелограмма — а также простые приёмы, о которых мы расскажем.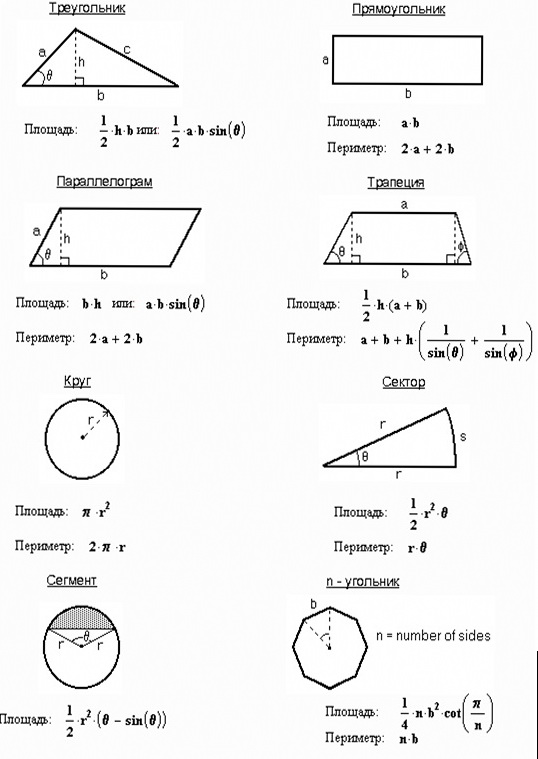
Для начала выучим формулы площадей фигур. Мы специально собрали их в удобную таблицу. Распечатайте, выучите и применяйте!
Конечно, не все формулы по геометрии есть в нашей таблице. Например, для решения задач по геометрии и стереометрии во второй части профильного ЕГЭ по математике применяются и другие формулы площади треугольника. О них мы обязательно расскажем.
Ты нашел то, что искал? Поделись с друзьями!
А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ.
1. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.
Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .
Ответ: .
2. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.
Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .
Ответ: .
3. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .
На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.
Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.
Ответ: .
Читайте также о задачах на тему «Координаты и векторы». Для их решения вспомните, что такое абсцисса точки (это ее координата по ) и что такое ордината (координата по ). Пригодятся также такие понятия, как координаты вектора и длина вектора (она находится по теореме Пифагора), синус и косинус угла, угловой коэффициент прямой, уравнение прямой, а также сумма, разность и скалярное произведение векторов, угол между векторами.
Площади фигур
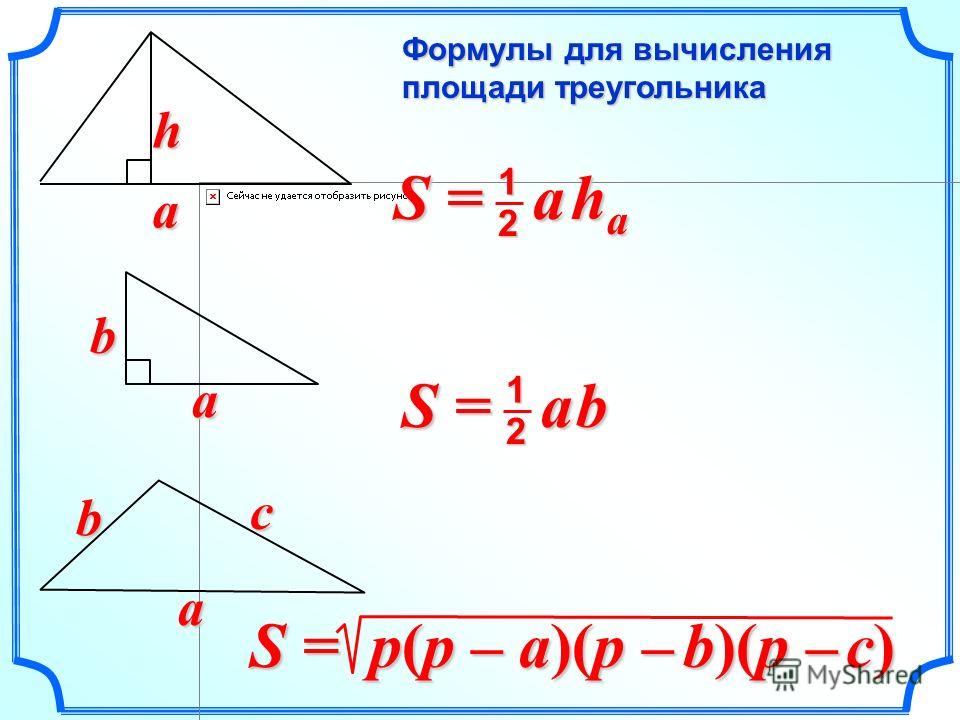
Формула площади треугольника
Площадь треугольника (S):
h — высота треугольника;
a — основание.
Площадь прямоугольного треугольника по катетам
Формула площади прямоугольного треугольника, (S):
a, b — катеты треугольника.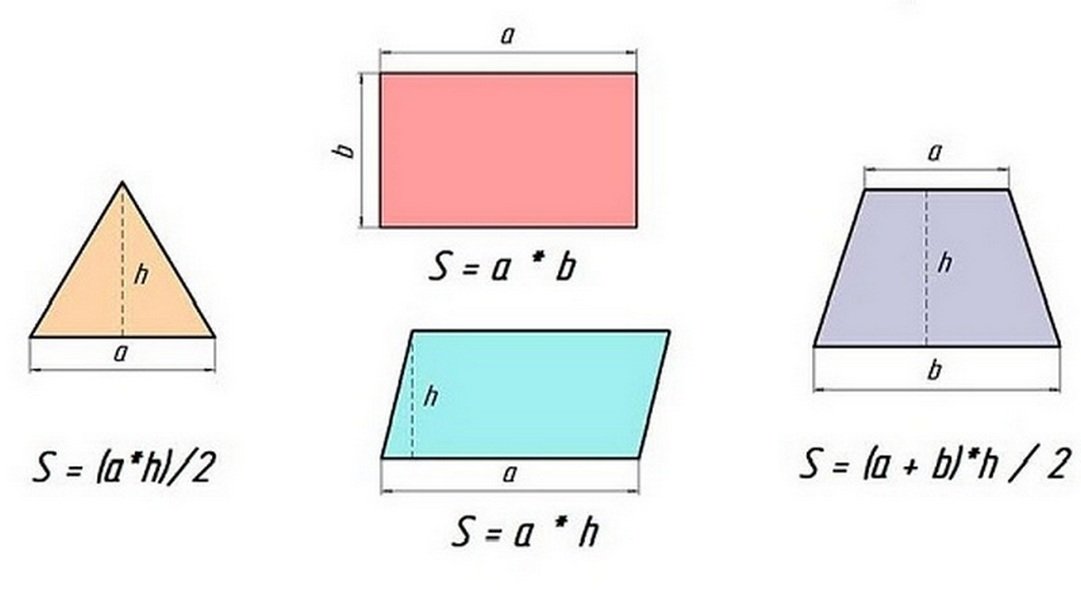
Площадь треугольника, формула Герона
Формула (Герона) площади треугольника через полупериметр (S):
a, b, c — стороны треугольника
p — полупериметр, p=(a+b+c)/2
Площадь равнобедренного треугольника
Площадь треугольника с двумя одинаковыми сторонами.
b — основание треугольника
a — равные стороны
h — высота
Формула площади треугольника через высоту h и основание b, (S):
Формула площади треугольника через, стороны a, b, (S):
Площадь равностороннего треугольника равна:
Формулы расчета, площади равностороннего треугольника.
a — сторона треугольника
h — высота
Площадь квадрата через диагональ
Как рассчитать площадь квадрата через диагональ
a — сторона квадрата
c — диагональ
Формула площади параллелограмма через сторону и высоту
a, b — стороны параллелограмма
Hb — высота на сторону b
Ha — высота на сторону a
Формула площади ромба
S = a · H
где: H — высота ромба.
a — сторона ромба
Площадь неравнобедренной трапеции :
a — нижнее основание;
b — верхнее основание;
h — высота трапеции.
Формула площади правильного многоугольника
a — сторона многоугольника
n — количество сторон
Записи по теме
Площади кругов и окружностей
Формулы площадей для кругов и окружностей: площадь круга, площадь сегмента круга, площадь кольца, площадь сектора кольца.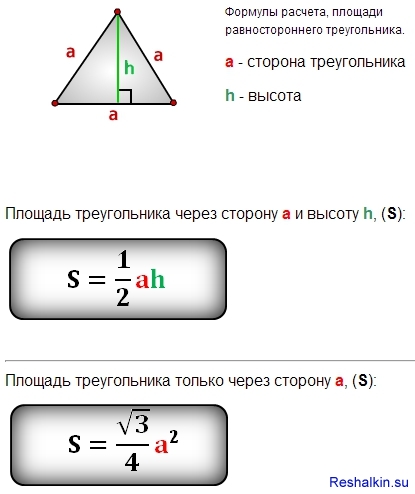
Площади поверхностей
Формулы площади поверхностей объёмных фигур. Формулы для расчёта площади поверхности куба, прямоугольного параллелепипеда, правильной и усечённой пирамид, усечённого конуса.
Площади многоугольников
\[{\Large{\text{Основные факты о площади}}}\]
Можно сказать, что площадь многоугольника — это величина, обозначающая часть плоскости, которую занимает данный многоугольник. За единицу измерения площади принимают площадь квадрата со стороной \(1\) см, \(1\) мм и т. 2 \Rightarrow
2 \Rightarrow
S_{\text{пр-к}}=ab \end{multline*}\)
Определение
Высота параллелограмма — это перпендикуляр, проведенный из вершины параллелограмма к стороне (или к продолжению стороны), не содержащей эту вершину.
Например, высота \(BK\) падает на сторону \(AD\), а высота \(BH\) — на продолжение стороны \(CD\):
Теорема: площадь параллелограмма
Площадь параллелограмма равна произведению высоты и стороны, к которой проведена эта высота.
Доказательство
Проведем перпендикуляры \(AB’\) и \(DC’\), как показано на рисунке. Заметим,что эти перпендикуляры равны высоте параллелограмма \(ABCD\).
Тогда \(AB’C’D\) – прямоугольник, следовательно, \(S_{AB’C’D}=AB’\cdot
AD\).
Заметим, что прямоугольные треугольники \(ABB’\) и \(DCC’\) равны. Таким образом,
\(S_{ABCD}=S_{ABC’D}+S_{DCC’}=S_{ABC’D}+S_{ABB’}=S_{AB’C’D}=AB’\cdot
AD. \)
\)
\[{\Large{\text{Площадь треугольника}}}\]
Определение
Будем называть сторону, к которой в треугольнике проведена высота, основанием треугольника.
Теорема
Площадь треугольника равна половине произведения его основания на высоту, проведенную к этому основанию.
Доказательство
Пусть \(S\) – площадь треугольника \(ABC\). Примем сторону \(AB\) за основание треугольника и проведём высоту \(CH\). Докажем, что \[S = \dfrac{1}{2}AB\cdot CH.\] Достроим треугольник \(ABC\) до параллелограмма \(ABDC\) так, как показано на рисунке:
Треугольники \(ABC\) и \(DCB\) равны по трем сторонам (\(BC\) – их общая сторона, \(AB = CD\) и \(AC = BD\) как противоположные стороны параллелограмма \(ABDC\)), поэтому их площади равны. Следовательно, площадь \(S\) треугольника \(ABC\) равна половине площади параллелограмма \(ABDC\), то есть \(S = \dfrac{1}{2}AB\cdot CH\).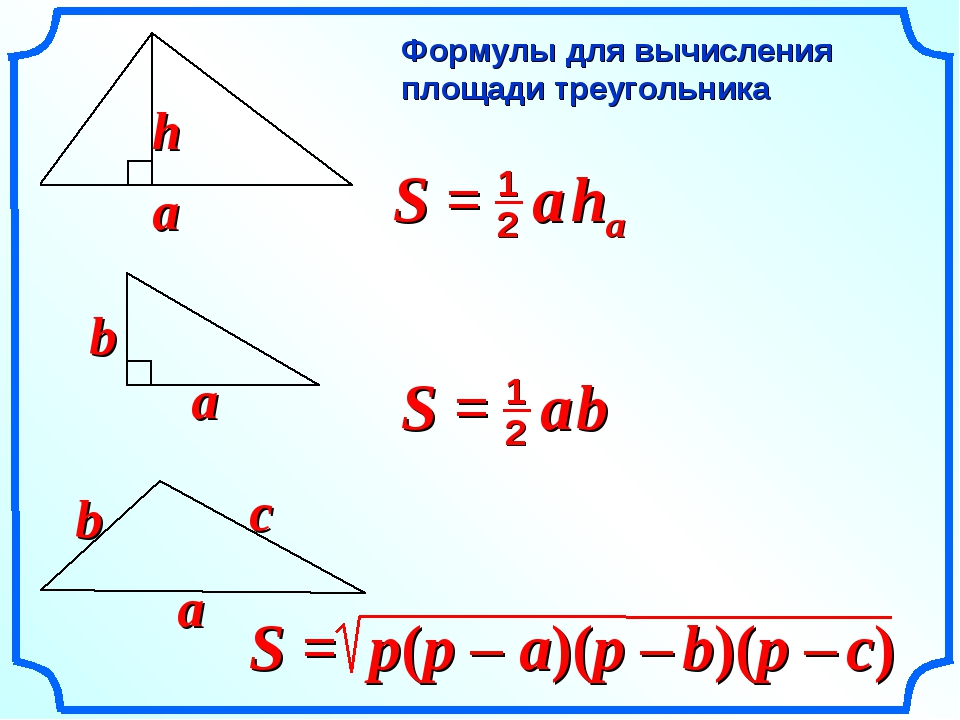
Теорема
Если два треугольника \(\triangle ABC\) и \(\triangle A_1B_1C_1\) имеют равные высоты, то их площади относятся как основания, к которым эти высоты проведены.
Следствие
Медиана треугольника делит его на два треугольника, равных по площади.
Теорема
Если два треугольника \(\triangle ABC\) и \(\triangle A_2B_2C_2\) имеют по равному углу, то их площади относятся как произведения сторон, образующих этот угол.
Доказательство
Пусть \(\angle A=\angle A_2\). Совместим эти углы так, как показано на рисунке (точка \(A\) совместилась с точкой \(A_2\)):
Проведем высоты \(BH\) и \(C_2K\).
Треугольники \(AB_2C_2\) и \(ABC_2\) имеют одинаковую высоту \(C_2K\), следовательно: \[\dfrac{S_{AB_2C_2}}{S_{ABC_2}}=\dfrac{AB_2}{AB}\]
Треугольники \(ABC_2\) и \(ABC\) имеют одинаковую высоту \(BH\), следовательно: \[\dfrac{S_{ABC_2}}{S_{ABC}}=\dfrac{AC_2}{AC}\]
Перемножая последние два равенства, получим: \[\dfrac{S_{AB_2C_2}}{S_{ABC}}=\dfrac{AB_2\cdot AC_2}{AB\cdot AC} \qquad \text{ или
} \qquad \dfrac{S_{A_2B_2C_2}}{S_{ABC}}=\dfrac{A_2B_2\cdot
A_2C_2}{AB\cdot AC}\]
Теорема Пифагора
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов:
Верно и обратное: если в треугольнике квадрат длины одной стороны равен сумме квадратов длин других двух сторон, то такой треугольник прямоугольный.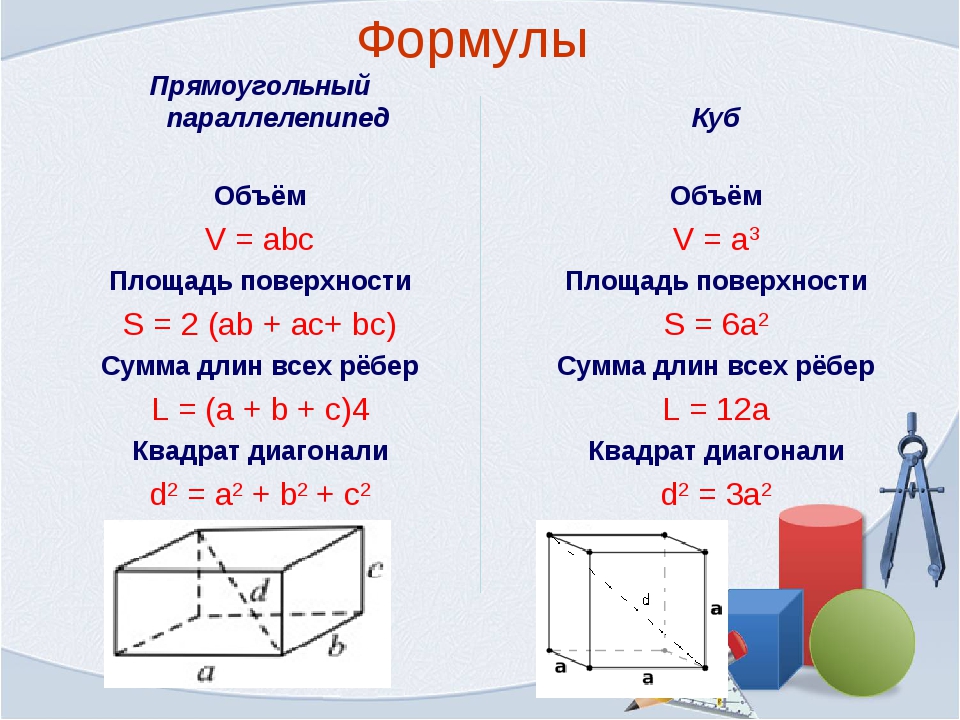
Теорема
Площадь прямоугольного треугольника равна половине произведения катетов.
Теорема: формула Герона
Пусть \(p\) – полупериметр треугольника, \(a\), \(b\), \(c\) – длины его сторон, тогда его площадь равна \[S_{\triangle}=\sqrt{p(p — a)(p —
b)(p — c)}\]
\[{\Large{\text{Площадь ромба и трапеции}}}\]
Замечание
Т.к. ромб является параллелограммом, то для него верна та же формула, т.е. площадь ромба равна произведению высоты и стороны, к которой проведена эта высота.
Теорема
Площадь выпуклого четырехугольника, диагонали которого перпендикулярны, равна половине произведения диагоналей.
Доказательство
Рассмотрим четырехугольник \(ABCD\). Обозначим \(AO=a, CO=b, BO=x,
DO=y\):
Заметим, что данный четырехугольник составлен из четырех прямоугольных треугольников, следовательно, его площадь равна сумме площадей этих треугольников:
\(\begin{multline*}
S_{ABCD}=\frac12ax+\frac12xb+\frac12by+\frac12ay=\frac12(ax+xb+by+ay)=\\
\frac12((a+b)x+(a+b)y)=\frac12(a+b)(x+y)\end{multline*}\)
Следствие: площадь ромба
Площадь ромба равна половине произведения его диагоналей: \[S_{\text{ромб}}=\dfrac12 d_1\cdot d_2\]
Определение
Высота трапеции – это перпендикуляр, проведенный из вершины одного основания к другому основанию.
Теорема: площадь трапеции
Площадь трапеции равна произведению полусуммы оснований на высоту.
Доказательство
Рассмотрим трапецию \(ABCD\) с основаниями \(BC\) и \(AD\). Проведем \(CD’\parallel AB\), как показано на рисунке:
Тогда \(ABCD’\) – параллелограмм.
Проведем также \(BH’\perp AD, CH\perp AD\) (\(BH’=CH\) – высоты трапеции).
Тогда \(S_{ABCD’}=BH’\cdot AD’=BH’\cdot BC, \quad S_{CDD’}=\dfrac12CH\cdot D’D\)
Т.к. трапеция состоит из параллелограмма \(ABCD’\) и треугольника \(CDD’\), то ее площадь равна сумме площадей параллелограмма и треугольника, то есть:
\[S_{ABCD}=S_{ABCD’}+S_{CDD’}=BH’\cdot BC+\dfrac12CH\cdot
D’D=\dfrac12CH\left(2BC+D’D\right)=\] \[=\dfrac12
CH\left(BC+AD’+D’D\right)=\dfrac12 CH\left(BC+AD\right)\]
Формулы площади
( пи
= = 3,141592 . ..)
..)
Площадь
Формулы
Примечание: «ab» означает «а»
умножить на «б». «a 2 » означает «квадрат»,
что то же самое, что «а» умножить на «а».
Будьте осторожны !! Количество единиц. Используйте то же самое
единиц для всех измерений. Примеры
квадрат = a 2
прямоугольник = ab
параллелограмм = bh
трапеция = h / 2 (b 1 + b 2 )
круг pi r 2
эллипс = pi r 1 r 2
| треугольник = | половина длины основания, умноженная на высоту треугольник |
| равносторонний треугольник = |
треугольник с учетом SAS (две стороны и противоположный угол)
= (1/2) a b sin C
треугольник, заданный a, b, c = [s (s-a) (s-b) (s-c)]
когда s = (a + b + c) / 2 (формула Герона)
правильный многоугольник = (1/2) n sin (360 ° / n) S 2
когда n = количество сторон и S = длина от центра до угла
Квартир
Площадь измеряется в «квадратных» единицах.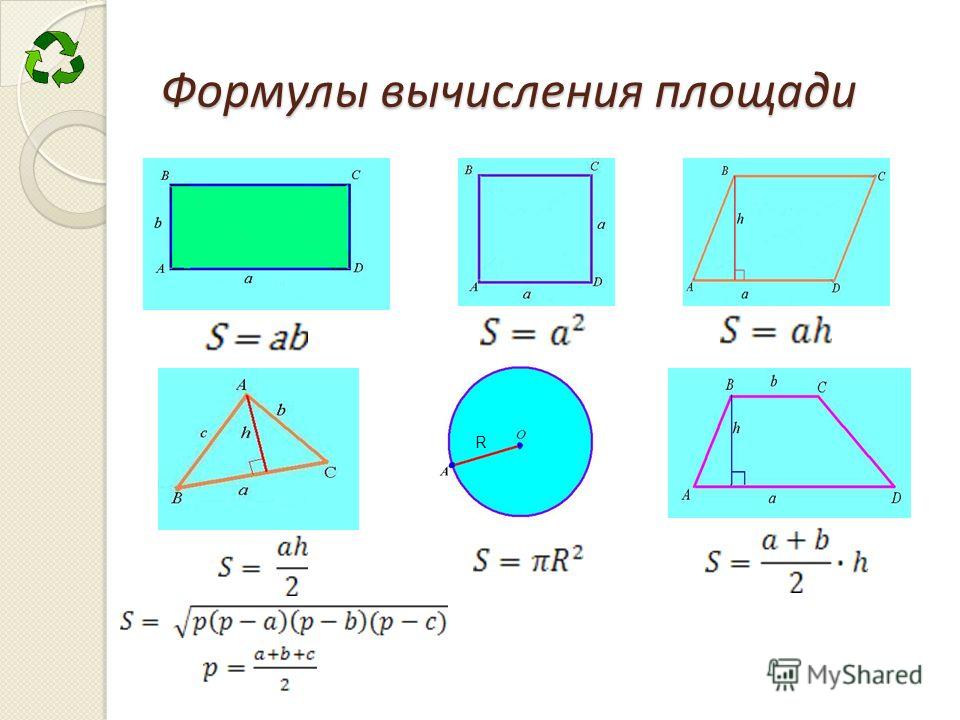 Площадь фигуры
Площадь фигуры
количество квадратов, необходимых для его полного покрытия, как плитки на
пол.
Площадь квадрата = сторона, умноженная на сторону. Поскольку каждая сторона квадрата — это
то же самое, это может быть просто длина одной стороны в квадрате.
Если у квадрата одна сторона 4 дюйма, площадь будет равна 4 дюймам.
4 дюйма или 16 квадратных дюймов. (Квадратные дюймы также можно записать в 2 .)
Обязательно используйте одни и те же единицы для всех измерений. Нельзя умножить футы на дюймы, квадрат не получается.
измерение.
Площадь прямоугольника — это длина сбоку.
раз больше ширины. Если ширина 4 дюйма, а длина 6 футов, что
это площадь?
НЕ ПРАВИЛЬНО …. 4 раза 6 = 24
ПРАВИЛЬНО …. 4 дюйма равны 1/3 фута. Площадь 1/3 фута
умножить на 6 футов = 2 квадратных фута. (или 2 кв. фута, или 2 фута 2 ).
(или 2 кв. фута, или 2 фута 2 ).
Формулы площади поверхности
| Формулы площади поверхности |
| (Математика | Геометрия | Формулы площади поверхности) |
( пи
= = 3,141592 …)
Поверхность
Формулы площади
В общем, площадь поверхности представляет собой сумму
все области всех форм, которые покрывают поверхность объекта.
Куб | Прямоугольный
Призма | Призма | Сфера
| Цилиндр | Единицы
Примечание: «ab» означает
«а», умноженное на «б». «а 2 » означает
«в квадрате», что то же самое, что «а» умножить на «а».
Будьте осторожны !! Количество единиц.
Используйте одни и те же единицы для всех измерений. Примеры
Примеры
| Площадь поверхности куба = 6 а 2 |
(а — длина стороны
каждый край куба)
Проще говоря, площадь поверхности куба — это площадь шести квадратов, которые
накрой это.Площадь одного из них a * a, или 2 . Поскольку эти
одинаковы, вы можете умножить одно из них на шесть, так что поверхность
площадь куба в 6 раз больше квадрата одной из сторон.
| Площадь поверхности прямоугольника Призма = 2ab + 2bc + 2ac |
(a, b и c —
длины трех сторон)
Проще говоря, площадь поверхности прямоугольной призмы равна площади шести
прямоугольники, которые его покрывают. Но нам не нужно вычислять все шесть, потому что
Но нам не нужно вычислять все шесть, потому что
мы знаем, что верх и низ одинаковы, передняя и задняя — это
то же самое, и левая и правая стороны одинаковы.
Площадь верха и низа (длины сторон a и
в) = а * с. Поскольку их два, вы получаете 2ac. Спереди и сзади
имеют длину стороны b и c. Площадь одного из них b * c, а там
их два, поэтому площадь поверхности этих двух равна 2bc. Левая и
правая сторона имеет длину сторон a и b, поэтому площадь поверхности одного из
их это а * б.Опять же, их два, поэтому их общая площадь поверхности
это 2ab.
| Площадь любой призмы |
(б — форма
концов)
Площадь поверхности = Боковая площадь + Площадь двух концов
(Боковая площадь) = (периметр формы b ) * L
Площадь поверхности = (периметр формы b ) * L + 2 * (Площадь формы b )
| Площадь поверхности сферы = 4 пи r 2 |
(r — радиус окружности)
| Площадь поверхности цилиндра = 2 pi r 2 + 2 pi r h |
(h — высота
цилиндра, r — радиус вершины)
Площадь поверхности = Области сверху и снизу + Площадь сбоку
Площадь поверхности = 2 (Площадь верха) + (периметр верха) * высота
Площадь поверхности = 2 ( пи r 2 ) + (2 пи r) * ч
На словах проще всего представить банку. Площадь поверхности — это
Площадь поверхности — это
площади всех частей, необходимых для закрытия банки. Это верх, низ,
и бумажная этикетка, которая оборачивается по центру.
Вы можете найти область вверху (или внизу). Это формула
для площади круга ( пи р 2 ). Так как есть и верх, и
дно, которое умножается на два.
Сторона похожа на этикетку банки. Если отклеить и положить
плоский это будет прямоугольник.Площадь прямоугольника — это произведение
с двух сторон. Одна сторона — это высота банки, другая —
периметр круга, так как этикетка один раз оборачивается вокруг банки. Так
площадь прямоугольника (2 пи r) * h.
Сложите эти две части вместе, и вы получите формулу поверхности.
площадь цилиндра.
Площадь поверхности = 2 ( пи r 2 ) + (2 пи r) * ч
Совет! Не забывайте единицы. |
Эти уравнения дадут вам правильные ответы, если вы будете держать единицы прямо.
Например — найти площадь поверхности куба со стороной 5 дюймов,
уравнение:
Площадь поверхности = 6 * (5 дюймов) 2
= 6 * (25 квадратных дюймов)
= 150 кв. Дюймов
Что такое площадь?
Площадь — это размер поверхности!
Пример:
У всех этих фигур одинаковая площадь 9:
Это помогает представить , сколько краски покроет форму.
Площадь простых форм
Для определенных форм существуют специальные формулы:
Пример: Какова площадь этого прямоугольника?
Формула:
Площадь = Ш × В
Ш = Ширина
В = Высота
Ширина равна 5, а высота равна 3, поэтому мы знаем, что w = 5 и h = 3 :
Площадь = 5 × 3 = 15
Узнайте больше в Area of Plane Shapes.
Площадь по счету квадратов
Также можно нанести фигуру на сетку и посчитать количество квадратов:
Прямоугольник имеет площадь 15
Пример: Когда каждый квадрат равен 1 метр со стороны, тогда площадь будет 15 м 2 (15 квадратных метров)
Квадратный метр против Квадратного метра
Базовая единица площади в метрической системе — квадратный метр. — квадрат, каждая сторона которого имеет 1 метр:
1 квадратный метр
Будьте осторожны, говоря «квадратные метры», а не «квадратные метры»:
Существуют также «квадратные мм», «квадратные см» и т. Д., Подробнее см. Метрическая площадь.
Приблизительная площадь при подсчете квадратов
Иногда квадраты не совсем соответствуют форме, но мы можем получить «приблизительный» ответ.
В одну сторону:
- больше чем половина квадрата считается как 1
- меньше чем половина квадрата считается как 0
Как это:
Этот пятиугольник имеет площадь приблизительно 17
Или мы можем сосчитать один квадрат, когда кажется, что областей в сумме дают .
Пример: Здесь область, отмеченная « 4 », кажется равной примерно 1 целому квадрату (также для « 8 »):
Этот круг имеет площадь приблизительно 14
Но лучше всего использовать формулу (когда это возможно):
Пример: круг имеет радиус 2,1 метра:
Формула:
Площадь = π × r 2
Где:
Радиус 2.1м , итого:
Площадь = 3,1416 … × (2,1 м) 2
= 3,1416 … × (2,1 м × 2,1 м)
= 13,854 … м 2
Итак, круг имеет площадь 13,85 квадратных метров (с точностью до 2 знаков после запятой)
Область сложных форм
Иногда мы можем разбить фигуру на две или более простые формы:
Пример: Какова площадь этой формы?
Разобьем область на две части:
Часть А — квадрат:
Площадь A = a 2 = 20 м × 20 м = 400 м 2
Часть B представляет собой треугольник. При взгляде сбоку он имеет основание 20 м и высоту 14 м.
При взгляде сбоку он имеет основание 20 м и высоту 14 м.
Площадь B = ½b × h = ½ × 20 м × 14 м = 140 м 2
Итак общая площадь:
Площадь = Площадь A + Площадь B
Площадь = 400 м 2 + 140 м 2
Площадь = 540м 2
Площадь путем сложения треугольников
Мы также можем разбить фигуру на треугольники:
Затем измерьте основание ( b ) и высоту ( h ) каждого треугольника:
Затем рассчитайте каждую площадь
(используя Area = ½b × h) и сложите их все.
Площадь по координатам
Когда мы знаем координаты каждой угловой точки, мы можем использовать метод «Площадь неправильных многоугольников».
Есть область многоугольника с помощью инструмента рисования, который тоже может помочь.
Формула площади и объема для геометрических фигур
пи (π) = 3,1415926535 . ..
..
9005 9
Формула периметра | |
| Квадрат | 4 × сторона |
| Прямоугольник | 2 × (длина + ширина) |
| Параллелограмм | 2 × (сторона1 + сторона2) |
| Треугольник | сторона1 + сторона2 + сторона3 |
| Правильный n-многоугольник | n × сторона |
| Трапеция | высота × (base1 + base2) / 2 |
| Trapezoid | base1 + base2 + height × [ csc (theta1) + csc (theta2)] |
| Окружность | 2 × pi × радиус |
| Эллипс | 4 × radius1 × E (k, pi / 2) E (k, pi / 2) — полный эллиптический интеграл второго рода k = (1 / radius1) × sqrt (radius1 2 — radius2 2 ) |
Формула площади | |
| Квадрат | сторона 2 |
| Прямоугольник | длина × ширина |
| Параллелограмм | основание × высота |
| Треугольник | основание × высота / 2 |
| Правильный n-многоугольник | (1/4) × n × сторона 2 × кроватка (pi / n) |
| Трапеция | высота × (base1 + base2) / 2 |
| Окружность | pi × радиус 2 |
| Эллипс | пи × радиус1 × радиус2 |
| Куб (поверхность) | 6 × сторона 2 |
| Сфера (поверхность) | 4 × пи × радиус 2 |
| Цилиндр ( вс r сторона стороны) | периметр круга × высота |
| 2 × pi × радиус × высота | |
| Цилиндр (вся поверхность) | Области верхнего и нижнего кругов + Площадь стороны |
| 2 (пи × радиус 2 ) + 2 × пи × радиус × высота | |
| Конус (поверхность) | пи × радиус × сторона |
| Тор (поверхность) | pi 2 × (радиус2 2 — радиус1 2 ) |
Формула объема | |
| Куб | сторона 3 |
| Прямоугольная призма | сторона1 × сторона2 × сторона3 |
| Сфера | (4 / 3) × пи × радиус 3 |
| Эллипсоид | (4/3) × пи × радиус1 × радиус2 × радиус3 |
| Цилиндр | пи × радиус 2 × высота |
| Конус | (1/3) × пи × радиус 2 × высота |
| Пирамида | (1/3) × (площадь основания) × высота |
| Тор | (1/4) × pi 2 × (r1 + r2) × (r1 — r2) 2 |
Источник: Spiegel, Murray R. Математический справочник формул и таблиц.
Математический справочник формул и таблиц.
Серия набросков Шаума по математике. McGraw-Hill Book Co., 1968.
Список всех площадей Формулы
Площадь четырехугольной призмы, объем
Используемая формула:
A L = P B x h
T A = A L + 2 x A B
В = A B x h
Где
A L = боковая область
P B = периметр основания
h = Высота
V = Объем
A B = Площадь основания
T A = Общая площадь
Связанный калькулятор:
Объем капсулы, площадь, окружность
Используемая формула:
Объем (V) = π r 2 ((4/3) r + a)
Площадь поверхности (S) = 2 π r (2 r + a)
Окружность (C) = 2 π r
Соответствующий калькулятор:
Объем, площадь поверхности и высота конической усадки
Используемая формула:
Объем V = (1/3) π h (r1 2 + r2 2 + (r1 * r2))
Высота наклона S = √ ( (r1 — r2) 2 + h 2 )
Площадь боковой поверхности L = π (r1 + r2) s
Площадь верхней поверхности T = π r1 2
Площадь базовой поверхности B = π r2 2
Общая площадь поверхности A = π (r1 2 + r2 2 + (r1 * r2) * s)
Соответствующий калькулятор:
Объем цилиндрической трубы
Формула:
Объем цилиндрической трубы = (h * PI * (r0 2 — r1 2 ))
Где,
h = Высота трубы,
r0, r1 = Радиусы трубы.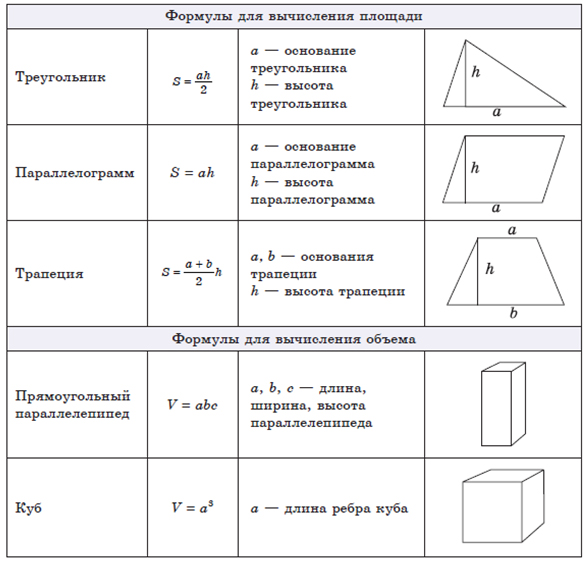
Связанный калькулятор:
Соотношение сторон и пиксели
Формула для определения соотношения сторон:
Соотношение сторон = a / b
пикселей = a * b
где,
a = Ширина изображения
b = Высота изображения
Связанный калькулятор:
Объем Barell
Формула:
Объем бочки = (h * PI * (2 * r1 2 + r2 2 ) / 3)
Где,
H = Высота ствол
r2, r2 = Радиусы ствола
Соответствующий калькулятор:
Преобразование прямоугольного в полярное
Используемая формула:
R = sqrt (х * х + у * у),
угол = атан (y / x)
Где,
Координаты прямоугольника:
x и y — горизонтальные и вертикальные расстояния от начала координат.
Полярные координаты (r, q):
r — расстояние от начала координат до точки.
q — угол, отсчитываемый от положительной оси x до точки.
t — угол (в градусах).
Связанный калькулятор:
Объем цилиндра с полусферическими концами
Формула:
Объем цилиндра = (PI * r 2 * h) + ((4/3) * PI * r 3 )
Где,
r = радиус цилиндра,
h = высота цилиндра.
Связанный калькулятор:
Апофема правильного многоугольника
Формула:
r = a / [2 tan (π / n)]
[или]
r = R cos (π / n)
Апофема правильного многоугольника
R = Окружной радиус
π = 3.14159
a = длина стороны
n = Число сторон
Соответствующий калькулятор:
Объем восьмиугольной пирамиды
Формула:
Объем восьмиугольной пирамиды = (B × h) / 3
Где
База (B) = 2 × s² (1 + √2)
s = длина стороны
h = Высота пирамиды
Связанный калькулятор:
Cicumcircle правильного многоугольника
Формула:
Circumradius (r) = l / (2 x sin (π / n))
Площадь многоугольника = (nxl 2 ) / (4 x tan (π / n))
Площадь окружности правильного многоугольника = 3.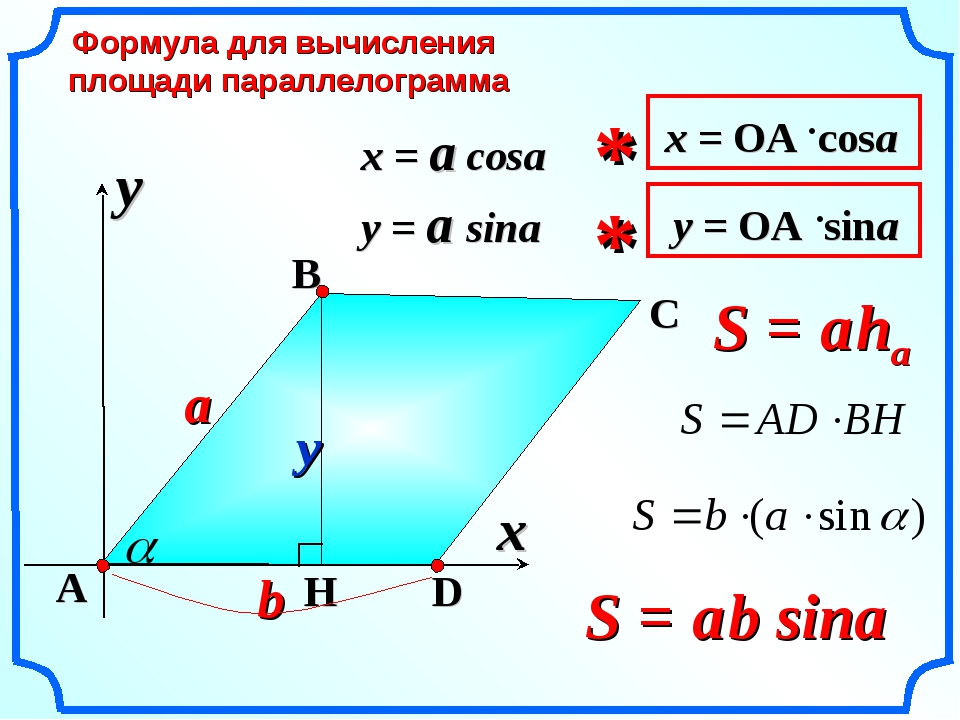 14 x r 2
14 x r 2
Где,
n = количество сторон многоугольника,
r = радиус описанной окружности,
l = длина стороны многоугольника
Связанный калькулятор:
Окружность правильного многоугольника
Используемая формула:
Inradius = l / 2 * tan (PI / n)
Площадь многоугольника = 0,5 * n * l * r
Площадь вписанной окружности = PI * r 2
Где,
n = количество сторон многоугольника,
r = Inradius,
l = длина стороны многоугольника
Связанный калькулятор:
Правильный многоугольник
Используемая формула:
Длина стороны многоугольника = 2 * r * sin (PI / n)
Площадь многоугольника = 0.5 * n * r 2 * sin (2PI / n)
Площадь круга = PI * r 2
Где,
n = количество сторон многоугольника,
r = Окружной радиус многоугольника
Соответствующий калькулятор:
Площадь восьмиугольной призмы, объем, площадь поверхности
Формула:
A = 2 × a × d
V = A × l
SA = (2 × A) + ( 8 × a × l)
Где,
a = длина стороны
l = высота
d = Расстояние
Связанный калькулятор:
Площадь сектора круга
Используемая формула:
Площадь сектора = 1/2 × радиус окружности × угол сектора
Связанный калькулятор:
Площадь трапеции
Используемая формула:
Площадь трапеции = (b1 + b2) / 2 × h
Связанный калькулятор:
Площадь и периметр стадиона
Используемая формула:
Площадь (A) = π r 2 + 2 r a
Периметр (P) = 2 (π r + a)
Связанный калькулятор:
Объем полого цилиндра, площадь, площадь поверхности, окружность
Используемая формула:
Окружность (C):
C1 = 2 π r1
C2 = 2 π r2
Площадь боковой поверхности (L):
L1 = 2 π r1 ч
L2 = 2 π r2 ч
Площадь (A):
A1 = π r1 2
A2 = π r2 2
А = А1 — А2
Объем (В):
V1 = π r1 2 ч
V2 = π r2 2 ч
В = V1 — V2
Толщина стенки трубы (т):
т = t1 — t2
Связанный калькулятор:
Объем аквариума
Формула:
Объем прямоугольника = l x b x h
где,
l = длина
b = ширина
h = высота
Объем цилиндра = π r 2 h
где,
r = радиус
h = высота
Соответствующий калькулятор:
Объем трубы
Используемая формула:
Объем трубы = π r 2 x высота
Соответствующий калькулятор:
Длина хорды окружности
Формула:
Длина хорды = 2√r 2 — d 2
где,
r = радиус окружности
d = перпендикулярное расстояние от хорды до центра окружности
Соответствующий калькулятор:
Длина дуги окружности
Формула:
Длина дуги окружности (S) = 2 x π xr (центральный угол / 360)
Где ,
r — Радиус дуги
Связанный калькулятор:
Площадь поверхности прямоугольной призмы, объем
Формула:
Площадь поверхности = 2 (wl + lh + hw)
Объем = w x l x h
Где,
w = ширина
l = длина
h = высота
Соответствующий калькулятор:
Градус Измерение сектора
Формула
Угол сектора = (A x 360) / π r 2
Где,
A = площадь сектора
r = радиус сектора
Соответствующий калькулятор:
Площадь кольцевого пространства
Формула:
A = π × (R 2 — H 2 )
Где,
A = Площадь кольцевого пространства (кольцевого)
R = радиус внешнего круга
H = радиус внутреннего круга
Связанный калькулятор:
LSA квадратной пирамиды
Формула:
L = a x √ (4h 2 + a 2 )
Где,
L = площадь боковой поверхности
h = Высота пирамиды
a = Сторона пирамиды
Связанный калькулятор:
Диагональ прямоугольника
Формула:
d = √ (w 2 + h 2 )
Где,
d = диагональ прямоугольника
w = Ширина
h = Высота
Соответствующий калькулятор:
Общая площадь прямоугольного правого клина
Формула:
S L = (1/2) * (a + c) * √ ((4 * h) + b 2 ) + (b * √ (h 2 + (ac) 2 ))
S B = ab
S = S L + S B
Где,
a = Сторона основания
b = ширина основания
c = Верхний край
h = высота
S L = площадь боковой поверхности
S B = Площадь основания
S = Общая площадь прямоугольного правого клина
Соответствующий калькулятор:
Площадь полукруга
Площадь полукруга Формула:
A = (1/2) * π * r 2
Где,
A = Площадь полукруга
r = Радиус
Соответствующий калькулятор:
Площадь и периметр масштабного треугольника
Формула:
Площадь = √ (s (sa) (sb) (sc))
s = (a + b + c) / 2
Периметр = a + b + c
где,
s — полупериметр.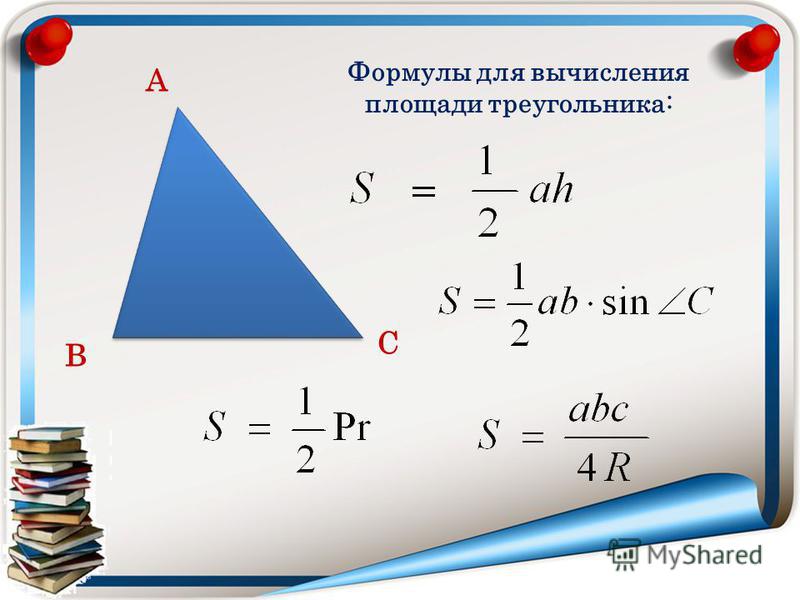
Связанный калькулятор:
Площадь правильного шестиугольника
Формула:
A = 3√3 (a 2 ) / 2
Где,
a = Длина стороны
A = Площадь
Связанный калькулятор:
Центральный угол окружности
Формула
Центральный угол = (Длина дуги x 180) / (3,142 x Радиус)
Связанный калькулятор:
Внешние углы выпуклого многоугольника
Формула:
N = 360 / (180-I)
Внешний угол в градусах = 180 — I
Где,
N = количество сторон выпуклого многоугольника
I = внутренний угол в градусах
Соответствующий калькулятор:
Площадь эллипса
Формула:
s = π (ab)
Где,
s = Площадь
a = Большая полуось (a)
b = Малая полуось (b)
Связанный калькулятор:
Градиент линии на плоскости
Формула:
k = (y 2 -y 1 ) / (x 2 -x 1 )
Где,
k = Гардиент линии
x1, x2, y1, y2 = Точка координат
Связанный калькулятор:
Площадь сегмента круга
Формула:
S = r 2 /2 (α π / 180 — sin α)
Где,
s = Площадь сегмента круга
α = центральный угол в градусах
r = радиус
sin = Sine
Связанный калькулятор:
Радиус вписанной окружности в октаэдре
Формула:
r = a√6 / 6
Где,
r = радиус вписанной окружности
a = Edge
Связанный калькулятор:
Радиус описанной окружности в октаэдре
Формула:
R = A √2 / 2
Где,
R = радиус описанной окружности
A = Длина кромки
Связанный калькулятор:
Площадь поверхности октаэдра
Формула:
S = 2a 2 √3
Где,
a = Edge
S = Площадь поверхности
Связанный калькулятор:
Объем октаэдра
Формула :
V = (A 3 √2) / 3
Где,
V = объем октаэдра
A = Edge
Связанный калькулятор:
Радиус вписанной окружности в Dod ecahedron
Формула:
r = a √ (10 (25 + 11√5)) / 2
Где,
r = радиус вписанной окружности
a = Edge
Соответствующий калькулятор:
Площадь a Сегмент окружности
Формула:
S = (R 2 /2) × (X-sin X)
Где,
S = Площадь отрезка окружности
R = Радиус
X = Центральный угол
Связанный калькулятор:
Боковая площадь наклонной призмы
Формула:
s = p * l
Где,
s = Боковая площадь наклонной призмы
p = периметр
l = боковой край
Связанный калькулятор:
Объем наклонной призмы
Формула:
v = bh
Где,
v = Объем призмы
b = Площадь базы
h = Высота
Соответствующий калькулятор:
Наклонная высота правильной пирамиды
Формула:
m = √ (b 2 — (a 2 /4))
Где,
м = наклонная высота
b = боковой край
a = Сторона основания
Связанный калькулятор:
Площадь боковой поверхности правильной пирамиды с использованием полупериметра
Формула:
S L = Полупериметр x (√ (b 2 — (a 2 /4)) )
Где,
S L = площадь боковой поверхности
b = боковой край
a = Сторона основания
Соответствующий калькулятор:
Площадь боковой поверхности правильной пирамиды с использованием основания и бокового края
Формула:
S L = 1/4 × n × a √ (4b 2 — a 2 )
Где,
n = Количество сторон
a = Сторона основания
b = боковой край
S L = Площадь боковой поверхности
Соответствующий калькулятор:
Площадь правильного шестиугольника
Формула:
S = (L / 2) * r
Где,
S = Площадь
L = периметр
r = Радиус вписанной окружности
Связанный калькулятор:
Высота правильной пирамиды
Формула:
Высота правильной пирамиды = (√ (4b 2 sin 2 (π / n) — a 2 )) / 2 sin (π / n)
Где,
b = боковой край
n = Количество сторон
a = Сторона основания
Связанный калькулятор:
Площадь боковой поверхности правильной пирамиды
Формула:
S L = (1/2) (периметр x наклонная высота)
Связанный калькулятор:
Общая площадь поверхности регулярной Пирамида
Формула:
S L = (1/4) xnx Длина основания x √ (4b 2 — Длина основания 2 )
S B = Полупериметр x Радиус
S = S L + S B
Где,
S = Общая площадь поверхности (TSA)
S B = Площадь основания
S L = Площадь боковой поверхности (LSA)
n = Количество сторон
b = Боковой край
Связанный калькулятор:
Объем правильной пирамиды на основе площади основания
Формула:
S B = Полупериметр x Радиус
V = (1/3) S B x Высота
Где,
V = объем правильной пирамиды
S B = Площадь основания
Соответствующий калькулятор:
Радиус вписанной окружности
Формула:
R = √ ((d1 2 d2 2 ) — (a — b) 2 (a + b) — p) 2 ) / (2p)
Где,
r = радиус вписанной окружности
d1, d2 = диагонали
a, b = стороны четырехугольника
p = периметр
Связанный калькулятор:
сегмент длины хорды окружности
Формула:
a = 2 √ (2hR — h 2 )
Где,
a = Хорда
h = Высота сегмента
R = радиус круга
Связанный калькулятор:
Высота сегмента круга
Формула:
h = R- (1/2) √ (4R 2 — a 2 )
Где,
h = Высота сегмента
R = радиус окружности
a = Хорда
Связанный калькулятор:
Сегмент периметра круга
Формула:
a = 2 √ (2hR — h 2 )
L = s + a
Где,
L = периметр
s = длина дуги
a = Хорда
h = Высота сегмента
R = радиус окружности
Связанный калькулятор:
Сегмент площади круга
Формула:
a = 2 √ (2hR — h 2 )
S = (1/2) * [sR — a (R — h) ]
Где,
S = Площадь
a = Хорда
s = длина дуги
R = радиус окружности
h = высота сегмента
Соответствующий калькулятор:
Общая площадь поверхности наклонной призмы
Формула:
s = pl + 2b
Где,
s = Общая площадь
p = периметр
l = боковой край
b = Площадь основания
Соответствующий калькулятор:
Длина дуги Стрелец
Формула:
Длина Стрельца = Радиус ± √ (Радиус 2 -Половина длины хорды 2 )
Связанный калькулятор:
Внутренние углы выпуклости Многоугольник
Формула:
N = 360 / E
Внутренний угол в градусах = 180 — E
Где,
N = количество сторон выпуклого многоугольника
E = внешний угол в градусах
Соответствующий калькулятор:
Наклонная высота пирамиды
Формула:
Наклонная высота = √ (h 2 + (b / 2) 2 )
Где,
h = высота пирамиды
b = основание пирамиды
Связанный калькулятор:
Наклонная высота квадратной пирамиды
Формула:
s 2 = h 2 + (1/4) a 2
Где,
s = наклонная высота квадратной пирамиды
h = высота
a = Длина стороны
Соответствующий калькулятор:
Высота треугольника шкалы
Формула:
h = (2 * k) / База
Где,
h = Высота масштабного треугольника
k = Площадь
База = длина основания
Соответствующий калькулятор:
Площадь вальмовой крыши
Формула:
H = (B x tan α) / 2
Обычные стропила = B / (2 x cos α)
Hip Rafters = √ (H 2 + (B 2 /2))
Площадь вальмовой крыши = 2 x Обычные стропила x Длина основания крыши
Где,
H = подъем крыши
B = Ширина основания крыши
α = Шаг крыши
tan = Касательная
cos = косинус
Связанный калькулятор:
Площадь трубы
Формула:
S = (2 * π * r 2 ) + (2 * π * h * r)
Где,
S = Площадь трубы
r = радиус
h = высота
Соответствующий калькулятор:
Площадь поверхности трубы
Формула:
S = (2π * (R 2 — r 2 )) + (2πh * (R + r))
Где,
S = Площадь поверхности трубы
R = Внешний радиус
r = внутренний радиус
h = Высота
Соответствующий калькулятор:
Площадь боковой поверхности цилиндра
Формула:
S = 2 x π x r x h
Где,
S = площадь боковой поверхности цилиндра
r = радиус
h = Высота
Соответствующий калькулятор:
Окружность круга
Формула:
C = 2 * 3.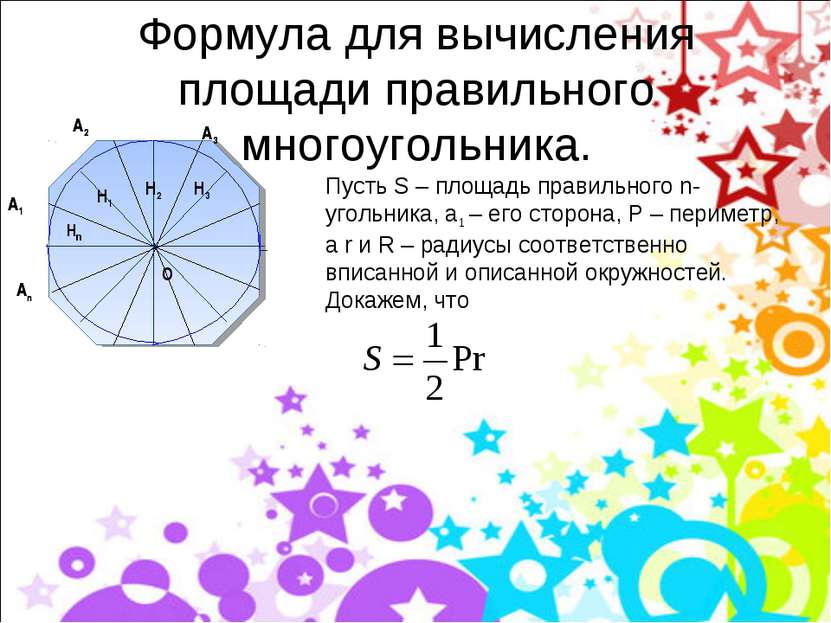 14 * r
14 * r
Где,
C = Окружность круга
r = радиус окружности
Соответствующий калькулятор:
Высота прямоугольной призмы
Формула:
h = v / a 2
Где,
h = высота / высота прямоугольной призмы
v = Объем
a = Площадь
Связанный калькулятор:
Радиус окружности
Формула:
r = c / (2 * π)
Где,
r = радиус круга
π = 3.14
c = Окружность круга
Связанный калькулятор:
Длина дуги
Формула:
r = (h / 2) + (w 2 / (8h))
C = 2 tan -1 (w / (2 × (rh)))
если (C <0)
C = 360 + C
l = C × 2 Π r / 360
Где,
r = радиус дуги
h = высота дуги
w = ширина дуги
C = центральный угол дуги
l = длина дуги
Соответствующий калькулятор:
Окружность эллипса
Формула:
C = 2 * π * √ ((a 2 + b 2 ) / 2)
Где
C = окружность эллипса
a = большая ось
b = вспомогательная ось
Связанный калькулятор:
Периметр правого треугольника
Формула:
P = a + b + √ (a 2 + b 2 )
Где,
p = периметр прямоугольного треугольника
a = высота
b = основание
Соответствующие Калькулятор:
Площадь круга
Формула круга:
Площадь круга = πr²
Диаметр круга = 2r
Окружность круга = 2 πr = πd
Площадь сектора = πr² (θ / 360)
Где,
r = радиус
Связанный калькулятор:
Калькулятор объема гиперсферы
Формула:
V = (1/2) * π 2 * r 4
Где,
V = объем гиперсферы
r = Радиус сферы
Соответствующий калькулятор:
Площадь изогнутой поверхности (CSA) кубоида
Формула:
A = 2h (l + b)
Где,
A = площадь криволинейной поверхности кубоида
h = высота
l = длина
b = ширина
Связанный калькулятор:
CSA цилиндра
Формула:
Площадь изогнутой поверхности = 2 × π × r × h
Где,
r = Радиус
h = Высота
Связанный калькулятор:
Додекагон
Формула:
Площадь = 3 × S 2 × (2 + √3)
Где,
s = Длина стороны
Связанный калькулятор:
Наклонная высота конуса
Формула :
Наклонная высота = √ ((r 2 ) + (h 2 ))
Где,
r = радиус
h = Высота
Соответствующий калькулятор:
Площадь поверхности конуса
Формула:
t = π × r × (l + r)
l = √ (r 2 + h 2 )
Где ,
t = Общая площадь поверхности
r = радиус
h = высота
l = наклонная высота
Соответствующий калькулятор:
Площадь изогнутой поверхности конуса
Формула:
c = π × r × l
l = √ (r 2 + h 2 )
Где,
c = изогнутая площадь поверхности
r = радиус
h = высота
l = наклонная высота
Соответствующий калькулятор:
Объем конуса
Формула:
Объем конуса = 1/3 × π × (r 2 × h)
Где,
r = радиус
h = Высота
Соответствующий калькулятор:
Диагональ прямоугольной призмы
Формула:
d = √l 2 + w 2 + h 2
Где,
d = Диагональ прямоугольной призмы
l = длина прямоугольной призмы
w = Ширина прямоугольной призмы
h = Высота прямоугольной призмы
Соответствующий калькулятор:
Площадь сегмента круга
Формула:
A = R² × (θ — sin (θ)) / 2
Где,
R = радиус
A = Площадь сегмента круга
θ = Центральный угол
Соответствующий калькулятор:
Апофема Пентагона
Формула:
Апофема Пентагона = a / [2 tan (π / n)]
Где,
a = длина стороны
n = 5
Связанный калькулятор:
Центроид параллелограмма
Формула:
X c = 0.

 Примеры
Примеры 