Формула объема тела: Все формулы объемов геометрических тел
- Геометрические фигуры ℹ️ формулы вычисления объема всех фигур и многогранников, обозначения и единицы измерения величины
- Урок 11. понятие объема — Геометрия — 11 класс
- Объемы геометрических тел – статья – Корпорация Российский учебник (издательство Дрофа – Вентана)
- Вычисление объемов тел вращения с помощью определенного интеграла
- Формулы объема
- формул объема для геометрических фигур.
- Калькулятор телесного жира
- Калькулятор площади поверхности тела
Геометрические фигуры ℹ️ формулы вычисления объема всех фигур и многогранников, обозначения и единицы измерения величины
Объём — это аддитивная функция от множества (мера), характеризующая вместимость области пространства, которую оно занимает. Изначально возникло и применялось без строгого определения в отношении тел трёхмерного евклидова пространства. Первые точные определения были даны Пеано (1887) и Жорданом (1892). Впоследствии понятие было обобщено Лебегом на более широкий класс множеств.
Для определения объёма существует несколько существенно различных подходов, которые дополняют друг друга и согласованы по конечному результату на «хороших множествах». Обычно под понятием объёма понимается мера Жордана, но иногда мера Лебега. Для римановых многообразий понятие объёма вводится аналогично понятию площади поверхности.
Все формулы объема геометрических тел
Объем куба
Объем куба равен кубу длины его грани.
Формула объема куба:
V = a 3
где:
V — объем куба,
a — длина грани куба.
Объем призмы
Объем призмы равен произведению площади основания призмы, на высоту.
Формула объема призмы:
где:
V- объем призмы,
So — площадь основания призмы,
h — высота призмы.
Объем параллелепипеда
Объем параллелепипеда равен произведению площади основания на высоту.
Формула объема параллелепипеда:
где:
V- объем параллелепипеда,
So — площадь основания,
h — длина высоты.
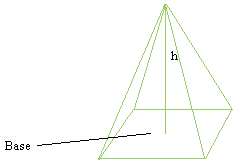
Объем пирамиды
Объем пирамиды равен одной трети произведения площади основания S (ABCDE) на высоту h (OS).
Формула объема пирамиды:
где:
V — объем пирамиды,
So — площадь основания пирамиды,
h — длина высоты пирамиды.
Объем усеченной пирамиды
Объем усеченной пирамиды равен одной трети произведения высоты h (OS) на сумму площадей верхнего основания S1(abcde), нижнего основания усеченной пирамиды S2 (ABCDE) и средней пропорциональной между ними.
Формула объема усеченной пирамиды:
Где:
S1 — площадь верхнего основания усеченной пирамиды,
S2 — площадь нижнего основания усеченной пирамиды,
h — высота усеченной пирамиды.
Объем цилиндра
Объем цилиндра равен произведению площади его основания на высоту.
Формула объема цилиндра:
V= π R2 h
V= Sоh
Где:
V — объем цилиндра,
So — площадь основания цилиндра,
R — радиус цилиндра,
h — высота цилиндра,
π = 3.141592
Объем правильной треугольной пирамиды
Объем правильной треугольной пирамиды равен одной трети произведения площади правильного треугольника, являющегося основанием S (ABC) на высоту h (OS).
Формула объема правильной треугольной пирамиды:
Где:
V — объем пирамиды;
h — высота пирамиды;
a — сторона основания пирамиды.
Объем конуса
Объем круглого конуса равен трети произведения площади основания S на высоту H.
Формула объема конуса:
Где:
V — объем конуса;
R — радиус основания;
H — высота конуса;
I — длина образующей;
S — площадь боковой поверхности конуса.
Объем усеченного конуса
Объем усеченного конуса равен разности объемов двух полных конусов.
Формула объема усеченного конуса:
Где:
V — объем усеченного конуса;
H — высота усеченного конуса;
R и R2 — радиусы нижнего и верхнего оснований.
Объем тетраэдра
Объем тетраэдра рассчитывается по классической формуле объема пирамиды. В нее нужно подставить высоту тетраэдра и площадь правильного (равностороннего) треугольника.
Формула тетраэдра:
Где:
V — объем тетраэдра;
a — ребро тетраэдра.
Объем шара
Объем шара равен четырем третьим от его радиуса в кубе перемноженного на число пи.
Формула объема шара:
Где:
V — объем шара;
R — радиус шара;
S — площадь сферы.
Объем шарового сегмента и сектора
Шаровый сегмент — это часть шара отсеченная плоскостью. В данном примере, плоскостью ABCD.
Формула объема шарового сегмента:
Где:
R — радиус шара
H — высота сегмента
π ≈ 3,14
Формула объема шарового сектора:
Где:
h — высота сегмента
R — радиус шара
π ≈ 3,14
Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
Формула объема прямоугольного параллелепипеда:
Где:
V — объем прямоугольного параллелепипеда,
a — длина,
b — ширина,
h — высота.
Урок 11. понятие объема — Геометрия — 11 класс
Геометрия, 11 класс
Урок №11
Понятие объёма
Перечень вопросов, рассматриваемых на уроке:
Понятие объёма.
Свойства объёмов.
Объём прямоугольного параллелепипеда.
Формула объёма прямоугольного параллелепипеда.
Тезаурус
Объём тела– величина, характеризующая часть пространства, занимаемую телом, и определяемая формой и линейными размерами этого тела.
Основные свойства объёма:
— равные тела имеют равные объёмы;
— если тело составлено из нескольких тел, то его объём равен сумме объёмов этих тел.
Основная литература:
Атанасян Л. С. и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10–11 классы [текст]: учеб. для общеобразоват. организаций: базовый и углубл. уровни – М.: Просвещение, 2014. – 255 с. С. 130–133.
Теоретический материал для самостоятельного изучения
С понятием объёмного тела, отличающегося от плоской фигуры, мы познакомились ещё в начальной школе.
Объёмом принято называть положительную величину, характеризующую часть пространства, занимаемую телом, и определяемую формой и линейными размерами этого тела.
Мы можем вычислить объём тела точно так же, как ранее находили площадь фигуры. Объём принято измерять в единицах измерения объёма (единицах измерения размера пространства, занимаемого телом), то есть в кубических метрах, сантиметрах, миллиметрах и так далее. За единицу измерения объёма можно принять куб с ребром 1 см, то есть, кубический сантиметр (обозначение: см3). По аналогии, можно за единицу измерения объёма принять кубический миллиметр (1 мм3), кубический метр (1 м3) и тому подобное.
Объём выражается в положительных числах. Это число показывает, сколько единиц измерения содержится в теле. Например, сколько кубических миллиметров в аквариуме, сколько кубических метровв бассейне и так далее.
Объём обозначается заглавной латинской буквой V.
Пример:
Объём книги400 кубических сантиметров запишут: V = 400см3.
Рассмотрим свойства объёмов.
Свойство № 1. Равные тела имеют равные объёмы. Это означает, что если два тела идентичны, то есть имеют равное количество единиц измерения и частей, то равны и их объёмы. Например, 2 одинаковых пакета молока равны в объёме.
Свойство № 2. Если тело составлено из нескольких тел, то его объём равен сумме объёмов этих тел.
Следствие из основных свойств объёмов.
Объём куба с ребром 1/n равен 1/n3
Доказательство. Рассмотрим куб, объём которого принят за единицу измерения объёмов, тоесть равный некоторому числукубических сантиметров. Его ребро равно единице измерения отрезков. Разобьём каждое ребро этого куба на произвольное количество частей – nтак, чтобы провести плоскости, перпендикулярные к этому ребру.
По второму свойству объёмов, сумма объёмов всех кубиков равна объёму всего куба (1 см3). Следовательно, поскольку мы разбили каждое ребро на n частей, то каждый маленький куб внутри большого куба будет иметь ребро
Объём каждого из маленьких кубиков при этом будет равен 1/n3.
Объём прямоугольного параллелепипеда
Теорема
Объём прямоугольного параллелепипеда равен произведению трёх его измерений.
Доказательство
Обозначимизмеренияпрямоугольного параллелепипеда P буквами a,b,c, его объём буквой V, и докажем, что V = a ∙ b ∙ c.
Рассмотрим два возможных случая.
Случай первый. Измерения a, b и c представляют собой конечные десятичные дроби, у которых число знаков после запятой не превосходит n (можно считать, что n больше или равно 1). В этом случае числа a ∙10n, b∙10n, c∙10n, являются целыми. Разобьём каждое ребро параллелепипеда на равные части длины: 1/10n и через точки разбиения проведём плоскости, перпендикулярные к этому ребру. Параллелепипед P разобьётся на abc∙103n равных кубов с ребром 1/10n. Так как объём каждого куба равен 1/103n, что мы доказали ранее, то объём всего параллелепипеда P = abc, что и требовалось доказать.
Случай второй.
Хотя бы одно из измерений a, b, c представляет собой бесконечную десятичную дробь. Рассмотрим конечные десятичные дроби: an, bn, cn, которые получаются из чисел a, b, c, если отбросить в каждом из них все цифры после запятой, начиная с n + 1. Очевидно, an ≤ a ≤ an’, где an’ = an+1 : 10n. Аналогичные неравенства справедливы для b и c. Перемножив эти неравенства, получим произведение anbncn ≤ abc ≤ an’bn’cn’, где bn’= bn+1 : 10n, cn’ = cn+1 : 10n
По доказанному в первом случае, левая часть неравенства представляет собой объём Vn прямоугольного параллелепипеда Pn с измерениями an, bn, cn, а правая часть – это объём Vn’ прямоугольного параллелепипеда Pn’ с измерениями an’, bn’, cn’. Так как параллелепипед P содержит в себе параллелепипед Pn, а сам содержится в параллелепипеде Pn’, то объём V параллелепипеда P заключён между Vn, = anbncn и Vn’= an’bn’cn’. Будем неограниченно увеличивать n. Тогда 1/10n будет становиться сколь угодно малым, и поэтому произведение an’bn’cn’ будет сколь угодно мало отличаться от числа, выраженного произведением anbncn. Отсюда следует, что число V сколь угодно мало отличается от числа, выраженного произведением anbncn, а значит, они равны.V = abc, что и требовалось доказать.
Примеры и разбор решения заданий тренировочного модуля.
№1.Длины сторон основания прямоугольного параллелепипеда равны 15 см и 20 см. Высота параллелепипеда равна диагонали основания. Найдите объём этого параллелепипеда.
Решение:
Найдём длину диагонали основания, для этого воспользуемся теоремой Пифагора:
А теперь найдём объём параллелепипеда:
V = 15 ∙ 20 ∙ 25 = 7500 см3
Ответ: V = 7500 см3.
№2.
Найдите площадь закрашенной фигуры, если объём прямоугольного параллелепипеда равен 960 см3, AB = 8 см, АА1= 20 см.
Варианты ответов:
220 см2
100 см2
400 см2
200 см2
Решение.
Найдём длину АD:
AD = 960 : 8 : 20 = 6 см
Найдём АС, воспользовавшись теоремой Пифагора:
Закрашенная фигура – прямоугольник. Вычислим его площадь: 10∙20= 200 см2.
Ответ: площадь закрашенной фигуры 200 см2.
Верный ответ: 200 см2.
Объемы геометрических тел – статья – Корпорация Российский учебник (издательство Дрофа – Вентана)
Объемы геометрических тел
Раньше для определения объемов геометрических тел традиционно использовались интегралы. Сегодня есть и другие подходы, которые подробно представлены в учебниках нашей корпорации. В одном из вебинаров «Российского учебника» учитель высшей категории Алексей Доронин рассказал о методах определения объема разных геометрических тел с помощью принципа Кавальери и других аксиом.
Определение объема
Объем можно определить как функцию V на множестве многогранников, удовлетворяющую следующим аксиомам:
- V сохраняется при движениях.
- V удовлетворяет принципу Кавальери.
- Если внутренности многогранников M и N не пересекаются, то V(M ∪ N) = V(M) + V(N).
- Объем прямоугольного параллелепипеда V = abc.
Принцип Кавальери (итальянского математика, ученика Галилея). Если при пересечении двух тел плоскостями, параллельными одной и той же плоскости, в сечениях этих тел любой из плоскостей получаются фигуры, площади которых относятся как m : n, то объемы данных тел относятся как m : n.
В открытом банке заданий ЕГЭ есть много задач для отработки этого способа определения объема.
Примеры
Задача 1. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.
Задача 2. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Задача 3. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Разберем, как можно вычислять объемы изучаемых в школе фигур.
Объем призмы
В представленном случае известны площадь основания и высота призмы. Чтобы найти объем, используем принцип Кавальери. Рядом с призмой (Ф2) поместим прямоугольный параллелепипед (Ф1), в основании которого — прямоугольник с такой же площадью, как у основания призмы. Высота у параллелепипеда такая же, как у наклонного ребра призмы. Обозначим третью плоскость (α) и рассмотрим сечение. В сечении виден прямоугольник с площадью S и, во втором случае, многоугольник тоже с площадью S. Далее вычисляем по формуле:
V Sосн h
Математика. Геометрия. Углублённый уровень. 11 класс. Задачник.
Задачник является Частью УМК для 10-11 классов, предназначенного для изучения предмета на углубленном уровне, и содержит более 1000 задач разной степени трудности, помогающих изучению и усвоению материала, изложенного в учебнике.
Пособие соответствует Федеральному государственному образовательному стандарту среднего (полного) общего образования.
Купить
Объем пирамиды
Лемма: две треугольные пирамиды с равновеликими основаниями и равными высотами равновелики. Докажем это, используя принцип Кавальери.
Возьмем две пирамиды одинаковой высоты и заключим их между двумя параллельными плоскостями α и β. Обозначим также секущую плоскость и треугольники в сечениях. Заметим, что отношения площадей этих треугольников связаны непосредственно с отношением оснований.
V 1/V2 = 1 <=> V1 = V2
Известно, что объем любой пирамиды равен одной трети произведения площади основания на высоту. Данной теоремой апеллируют довольно часто. Однако откуда в формуле объема пирамиды появляется коэффициент 1/3? Чтобы понять это, возьмем призму и разобьем ее на 3 треугольные пирамиды:
V1 = V2
V2 = V3
Vпризмы S h = 3V
V = 1/3 Sh
Объем цилиндра
Возьмем прямой круговой цилиндр, в котором известны радиус основания и высота. Рядом поместим прямоугольный параллелепипед, в основании которого лежит квадрат. Рассмотрим:
Vцил = πh × R2
Объем конуса
Конус лучше всего сравнивать с пирамидой. Например, с правильной четырехугольной пирамидой с квадратом в основании. Две фигуры с равными высотами заключаем в две параллельные плоскости. Обозначив третью плоскость, в сечении получаем круг и квадрат. Представления о подобиях приводят к числу π.
SФ1/SФ2 = π
Vконуса = 1/3 πR2 h
Что ещё почитать?
Объем шара
Объем шара — одна из наиболее сложных тем. Если предыдущие фигуры можно продуктивно разобрать за один урок, то шар лучше отложить на последующее занятие.
Чтобы найти объем шара, шар часто предлагается сравнить со сложным геометрическим телом, которое связано с конусом и цилиндром. Но не стоит строить цилиндр, из которого вырезан конус, или вроде того. Возьмем половину шара с высотой R и радиусом R, а также конус и цилиндр с аналогичными высотами и радиусами оснований. Обратимся к полезным материалам на сайте
«Математические этюды», где объем шара рассматривается с использованием весов Архимеда. Цилиндр располагается на одной стороне уравновешенных весов, конус и половина шара — на другой.
Заключаем геометрические фигуры в две параллельные плоскости и смотрим, что получается в сечении. У цилиндра — круг с площадью πR2. Как известно, если внутренности геометрических тел не пересекаются, то объем их объединения равен сумме объемов. Пусть в конусе и в половине шара расстояние до плоскости сечения будет x. Радиус — тоже x. Тогда площадь сечения конуса — π ∙ x2. Расстояние от середины верха половины шара к краю сечения — R. Площадь сечения половины шара: π(R2 — x2).
Заметим, что: πR2 + πR2 — πR2 = πR2
Vцил = πR2 × R = πR3 = 1/3 R3 π + Vшара
Vшара = 4/3 πR3
Итак, чтобы найти объем нового, не изученного геометрического тела, нужно сравнить его с тем телом, которое наиболее на него похоже. Многочисленные примеры заданий из открытого банка задач показывают, что в работе с фигурами имеет смысл использовать представленные формулы и аксиомы.
#ADVERTISING_INSERT#
Вычисление объемов тел вращения с помощью определенного интеграла
Тип урока:
комбинированный.
Цель урока: научиться вычислять объемы тел вращения с помощью
интегралов.
Задачи:
- закрепить умение выделять криволинейные трапеции из ряда геометрических
фигур и отработать навык вычислений площадей криволинейных трапеций; - познакомиться с понятием объемной фигуры;
- научиться вычислять объемы тел вращения;
- способствовать развитию логического мышления, грамотной математической
речи, аккуратности при построении чертежей; - воспитывать интерес к предмету, к оперированию математическими понятиями
и образами, воспитать волю, самостоятельность, настойчивость при достижении
конечного результата.
Ход урока
I. Организационный момент.
Приветствие группы. Сообщение учащимся целей урока.
Рефлексия.
Спокойная мелодия.
– Сегодняшний урок мне бы хотелось начать с притчи. “Жил мудрец, который знал
все. Один человек захотел доказать, что мудрец знает не все. Зажав в ладонях
бабочку, он спросил: “Скажи, мудрец, какая бабочка у меня в руках: мертвая или
живая?” А сам думает: “Скажет живая – я ее умертвлю, скажет мертвая – выпущу”.
Мудрец, подумав, ответил: “Все в твоих руках”. (Презентация.
Слайд)
– Поэтому давайте сегодня плодотворно поработаем, приобретем новый багаж
знаний, и полученные умения и навыки будем применять в дальнейшей жизни и в
практической деятельности. “Все в Ваших руках”.
II. Повторение ранее изученного материала.
– Давайте вспомним основные моменты ранее изученного материала. Для этого
выполним задание “Исключите лишнее слово”. (Слайд.)
(Учащийся выходит к И.Д.с помощью ластика убирает лишнее слово.)
– Правильно “Дифференциал”. Попробуйте
оставшиеся слова назвать одним общим словом. (Интегральное исчисление.)
– Давайте вспомним основные этапы и понятия связанные с интегральным
исчислением..
“Математическая гроздь”.
Задание. Восстановите пропуски. (Студент выходит и вписывает ручкой
необходимые слова.)
– Реферат о применении интегралов мы заслушаем позже.
Работа в тетрадях.
– Формулу Ньютона-Лейбница вывели английский физик Исаака Ньютона (1643–1727)
и немецкий философ Готфрида Лейбница (1646–1716). И это не удивительно, ведь
математика – язык, на котором говорит сама природа.
– Рассмотрим, как при решении практических заданий используется эта формула.
Пример 1:
Вычислить площадь фигуры, ограниченной линиями
Решение:
Построим на координатной плоскости графики функций
.
Выделим площадь фигуры, которую надо найти.
III. Изучение нового материала.
– Обратите внимание на экран. Что изображено на первом рисунке? (Слайд)
(На рисунке представлена плоская фигура.)
– Что изображено на втором рисунке? Является ли эта фигура плоской?
(Слайд) (На рисунке представлена объемная фигура.)
– В космосе, на земле и в повседневной жизни мы встречаемся не только с
плоскими фигурами, но и объемными, а как же вычислить объем таких тел? Например
объем планеты, каметы, метеорита, и т.д.
– Об объеме задумываются и строя дома, и переливая воду из одного сосуда в
другой. Правила и приёмы вычисления объёмов должны были возникать, другое дело,
насколько они были точны и обоснованны.
Сообщение студентки. (Тюрина Вера.)
1612 год был для жителей австрийского города Линц, где жил тогда известный
астроном Иоганн Кеплер очень урожайным, особенно на виноград. Люди заготовляли
винные бочки и хотели знать, как практически определить их объёмы. (Слайд 2)
– Таким образом, рассмотренные работы Кеплера положили начало целому потоку
исследований, увенчавшихся в последней четверти XVII в. оформлением в трудах И.
Ньютона и Г.В. Лейбница дифференциального и интегрального исчисления. Математика
переменных величии заняла с этого времени ведущее место в системе математических
знаний.
– Вот сегодня мы с вами и займемся такой практической деятельностью,
следовательно,
Тема нашего урока: “Вычисление объемов тел вращения с помощью определенного
интеграла”. (Слайд)
– Определение тела вращения вы узнаете, выполнив следующее задание.
“Лабиринт”.
Лабиринт (греческое слово) означает ход в подземелье. Лабиринт– запутанная
сеть дорожек, ходов, сообщающихся друг с другом помещений.
Но определение “разбилось”, остались подсказки в виде стрелок.
Задание. Найдите выход из запутанного положения и запишите определение.
Слайд. “Карта инструктаж” Вычисление объемов.
При помощи определенного интеграла можно вычислить объем того или иного тела,
в частности, тела вращения.
Телом вращения называется тело, полученное вращением криволинейной трапеции
вокруг ее основания (рис. 1, 2)
Объем тела вращения вычисляется по одной из формул:
1.,
если вращение криволинейной трапеции вокруг оси ОХ.
2. ,
если вращение криволинейной трапеции вокруг оси ОУ.
Карту инструктаж получает каждый студент. Преподаватель подчеркивает основные
моменты.
– Преподаватель объясняет решение примеров на доске.
Пример.
Рассмотрим отрывок из известной сказки А. С. Пушкина “Сказка о царе Салтане,
о сыне его славном и могучем богатыре князе Гвидоне Салтановиче и о прекрасной
царевне Лебеде” (Слайд 4):
…..
И привез гонец хмельной
В тот же день приказ такой:
“Царь велит своим боярам,
Времени не тратя даром,
И царицу и приплод
Тайно бросить в бездну вод”.
Делать нечего: бояре,
Потужив о государе
И царице молодой,
В спальню к ней пришли толпой.
Объявили царску волю –
Ей и сыну злую долю,
Прочитали вслух указ,
И царицу в тот же час
В бочку с сыном посадили,
Засмолили, покатили
И пустили в окиян –
Так велел-де царь Салтан.
(Слайд 5):
Какими же должен быть объем бочки, чтобы в ней поместились царица и её сын?
– Рассмотрим следующие задания
1. Найти объем тела, получаемого вращением вокруг оси ординат криволинейной
трапеции, ограниченной линиями: x2 + y2
= 64, y = -5, y = 5, x = 0.
Решение.
Ответ : 1163 cm3.
Найти объем тела, получаемого вращением параболической трапеции, вокруг оси
абсцисс y =
, x = 4, y = 0.
Решение .
IV. Закрепление нового материала
Пример 2. Вычислить объем тела, образованного вращением лепестка, вокруг оси
абсцисс y = x2, y2
= x.
Решение .
Построим графики функции. y = x2, y2
= x. График y2 = x
преобразуем к виду y =
.
Имеем V = V1 – V2
Вычислим объем каждой функции
– Теперь, давайте, рассмотрим башню для
радиостанции в Москве на Шаболовке, построенной по проекту замечательного
русского инженера, почётного академика В. Г. Шухова. Она состоит из частей –
гиперболоидов вращения. Причём, каждый из них изготовлен из прямолинейных
металлических стержней, соединяющих соседние окружности (рис.8, 9).
– Рассмотрим задачу.
Найти объем тела, получаемого вращением дуг гиперболы
вокруг
ее мнимой оси, как показано на рис. 8, где
Решение.
куб. ед.
Задания по группам. Учащиеся вытягивают жребий с задачами, рисунки
выполняют на ватмане, один из представителей группы защищает работу.
1-я группа.
Удар! Удар! Ещё удар!
Летит в ворота мячик – ШАР!
А это– шар арбузный
Зелёный, круглый, вкусный.
Вглядитесь лучше – шар каков!
Он сделан из одних кругов.
Разрежьте на круги арбуз
И их попробуйте на вкус.
Найти объем тела, получаемого вращением вокруг оси ОХ функции, ограниченную
Решение.
Ошибка! Закладка не определена.
– Скажите, пожалуйста, где мы встречаемся с данной фигурой?
Дом. задание для 1 группы. ЦИЛИНДР (слайд) .
«Цилиндр – что такое?» – спросил я у папы.
Отец рассмеялся: Цилиндр – это шляпа.
Чтобы иметь представление верное,
Цилиндр, скажем так, это банка консервная.
Труба парохода – цилиндр,
Труба на нашей крыше – тоже,
Все трубы на цилиндр похожи.
А я привёл пример такой –
Калейдоскоп любимый мой,
Глаз от него не оторвёшь,
И тоже на цилиндр похож.
– Задание. Домашняя работа составить график функции и вычислить объем .
2-я группа. КОНУС
(слайд).
Сказала мама: А сейчас
Про конус будет мой рассказ.
В высокой шапке звездочёт
Считает звёзды круглый год.
КОНУС – шляпа звездочёта.
Вот какой он. Понял? То-то.
Мама у стола стояла,
В бутылки масло разливала.
– Где воронка? Нет воронки.
Поищи. Не стой в сторонке.
– Мама, с места я не тронусь,
Формулы объема
Здесь мы предлагаем вам формулы объема для некоторых распространенных трехмерных фигур, а также для эллипсоида и полого цилиндра, которые встречаются не так часто.
Куб:
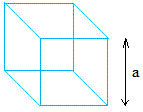 |
Объем = a 3 = a × a × a
Цилиндр:
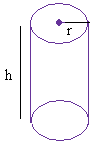 |
Объем = π × r 2 × h
π = 3.14
h — высота
r — радиус
Прямоугольное тело или кубоид:
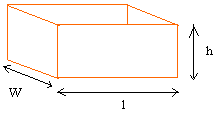 |
Объем = l × w × h
l — длина
w — ширина
h — высота
Сфера:
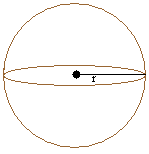 |
Объем = (4 × π × r 3 ) / 3
π = 3,14
r — радиус
Конус:
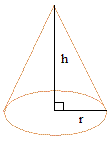 |
Объем = (π × r 2 × h) / 3
pi = 3.14
r — радиус
h — высота
Пирамида:
 |
Объем = (B × h) / 3
B — площадь основания
h — высота
Немного менее распространенные формулы объема
Эллипсоид: 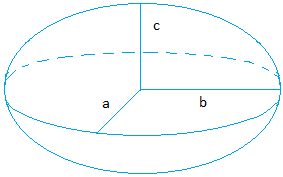
Объем = (4 × π × a × b × c) / 3
Используйте π = 3,14
Полый цилиндр: 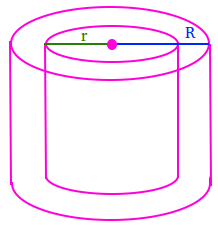
Объем = π × R 2 × h — π × r 2 × h
Объем = π × h (R 2 — r 2 )
Используйте π = 3.14.
Как использовать формулы объема для расчета объема.
Куб
Длина стороны = a = 2 см
Объем = (2 см) = 2 см × 2 см × 2 см = 8 см 3
Цилиндр
Высота 8 дюймов и радиус 2 дюйма.
Объем = π × r 2 × h = 3,14 × (2 дюйма) 2 × 8 дюймов = 3,14 × 4 × 8 дюймов = 3,14 × 4 × 8 дюймов 3
Объем = 3,14 × 32 дюймов 3 = 100,48 дюймов 3
Прямоугольный цельный или прямоугольный
Длина 6 см, ширина 3 см и высота 5 см.
Объем = д × ш × в = 6 × 3 × 5 = 90 см 3
Сфера
Радиус = r = 20
Объем = (4 × π × r 3 ) / 3 = [4 × 3,14 × (20) 3 ] / 3 = 3,14 × (20) 3 × 4
Объем = 3,14 × 8000 × 4 = 3,14 × 32000 = 100480
Конус
Радиус равна 3, а высота равна 4.
Объем = (π × r 2 × h) / 3 = [3,14 × (3) 2 × 4] / 3 = 3.14 × 9 × 4
Объем = 3,14 × 36 = 113,04
Пирамида
Пирамида имеет высоту 6 футов. Если основание пирамиды представляет собой квадрат длиной 2 фута, найдите объем.
Объем = (B × h) / 3
B = площадь основания = 2 фута × 2 фута = 4 фута 2
Объем = (4 × 6) / 3 фута 3 = 24/3 фута 3 = 8 футов 3
Эллипсоид
Радиусы эллипсоида составляют 1 см, 2, см и 3 см.
Объем = (4 × π × a × b × c) / 3 = (4 × 3,14 × 1 × 2 × 3) / 3
Объем = (3,14 × 4 × 6) / 3 = (3,14 × 24) / 3 = 81,64 / 3 = 25,12 см 3
Полый цилиндр
Внешний радиус 8, внутренний радиус 6 и высота 10.
Объем = π × h (R 2 — r 2 ) = π × 10 (8 2 — 6 2 ) = π × 10 (64 — 36)
Объем = π × 10 (28) = π × 280 = 879,2
Классные математические уловки
7 окт, 20 13:37

Хотите произвести впечатление на своих друзей? Ознакомьтесь с этими классными математическими приемами, которые помогут вам без особых усилий решать сложные базовые математические задачи.
Подробнее
Новые уроки математики
Ваша электронная почта в безопасности. Мы будем использовать его только для информирования вас о новых уроках математики.
.
формул объема для геометрических фигур.
Объем
— это объем пространства, занимаемого объектом; измеряется в кубических единицах.
Объем куба
Объем куба равен длине его ребра куба.
Формула объема куба:
В = а 3
где V — объем куба,
а — длина ребра.
Объем призмы
Объем призмы равен произведению площади основания на высоту призмы.
Формула объема призмы:
V = A b h
где V — объем призмы,
A b — площадь основания призмы,
h — высота призмы.
Объем параллелепипеда
Объем параллелепипеда равен произведению площади основания на высоту параллелепипеда.
Формула объема параллелепипеда:
V = A b · h
где V — объем параллелепипеда,
A b — площадь основания параллелепипеда,
ч — высота параллелепипеда.
Объем прямоугольной призмы
Объем прямоугольной призмы равен произведению ее длины, ширины и высоты.
Формула объема прямоугольной призмы:
V = a · b · h
где V — объем прямоугольной призмы,
а — длина,
б — ширина,
h — высота.
Объем пирамиды
Объем пирамиды равен одной трети произведения площади ее основания на высоту.
Формула объема пирамиды:
где V — объем пирамиды,
A b — площадь основания пирамиды,
ч — высота пирамиды.
Объем тетраэдра
Объемные формулы тетраэдра:
где V — объем тетраэдра,
а — длина кромки.
Объем правого кругового цилиндра
Объем правого кругового цилиндра равен произведению площади его основания на высоту.
Формула объема правого кругового цилиндра:
V = π R 2 ч
V = A b h
где V — объем цилиндра,
A b — площадь основания,
R — радиус основания,
h — высота,
π = 3,141592.
Объем правого кругового конуса
Объем правого кругового конуса равен одной трети произведения площади его основания на высоту.
Формула объема правого кругового конуса:
где V — объем конуса,
A b — площадь основания,
R — радиус основания,
h — высота,
π = 3,141592.
Объем сферы (твердый)
Объем сферы равен четырем третям ее куба радиуса, умноженным на число пи.
Формула объема шара (твердого тела):
где V — объем шара,
R — радиус шара,
π = 3.141592.
.
Калькулятор телесного жира
Калькулятор жира в организме можно использовать для оценки общего жира в организме на основе конкретных измерений. Используйте вкладку «Метрические единицы», если вам удобнее пользоваться Международной системой единиц (СИ). Чтобы получить наилучшие результаты, измеряйте с точностью до 0,5 см (1/4 дюйма). Этот расчет основан на методе ВМС США, но также включает расчет процентного содержания жира в организме с использованием метода ИМТ (оба из которых описаны ниже).
Результат
Жир: 15.3%
| 15,3% |
| Жир (метод ВМС США) | 15,3% |
| Категория жира тела | Фитнес |
| Жировая масса тела | 23,2 фунта |
| Безжировая масса тела | 128,8 фунта |
| Идеальный жир для данного возраста (Джексон и Поллард) | 10,5% |
| Потеря жира для достижения идеала | 7.2 фунта |
| Жир (метод ИМТ) | 15,4% |
Связанный калькулятор BMI | Калькулятор калорий | Калькулятор идеального веса
Артикул
Диапазоны телесного жира 1
| Описание | Женщины | Мужчины |
| Рекомендуемое количество | 20-25% | 8-14% |
| Взрослые в США, в среднем | 22-25% | 15-19% |
| Ожирение | 30 +% | 25 +% |
Американский совет по классификации жировых отложений при упражнениях
| Описание | Женщины | Мужчины |
| Незаменимый жир | 10-13% | 2-5% |
| Спортсмены | 14-20% | 6-13% |
| Фитнес | 21-24% | 14-17% |
| Среднее значение | 25-31% | 18-25% |
| Ожирение | 32 +% | 25 +% |
Джексон & Pollard Идеальное процентное содержание жира в организме
| Возраст | Женщины | Мужчины |
| 20 | 17.7% | 8,5% |
| 25 | 18,4% | 10,5% |
| 30 | 19,3% | 12,7% |
| 35 | 21,5% | 13,7% |
| 40 | 22,2% | 15,3% |
| 45 | 22,9% | 16,4% |
| 50 | 25,2% | 18,9% |
| 55 | 26,3% | 20,9% |
Жир, избыточный вес и ожирение
Научный термин для обозначения телесного жира — «жировая ткань».«Жировая ткань выполняет ряд важных функций. Ее основная цель — накапливать липиды, из которых тело вырабатывает энергию. Кроме того, она выделяет ряд важных гормонов и обеспечивает тело некоторой амортизацией, а также изоляцией. 1
Телесный жир включает основной телесный жир и накопленный телесный жир. Незаменимый жир тела — это базовый уровень жира, который содержится в большинстве частей тела. Это необходимый жир, поддерживающий жизнь и репродуктивные функции. Количество незаменимого жира различается между мужчинами и женщинами и обычно составляет около 2-5% у мужчин и 10-13% у женщин.Здоровый диапазон жировых отложений для мужчин обычно составляет 8-19%, а для женщин — 21-33%. Хотя избыток жира в организме может иметь множество пагубных последствий для здоровья человека, недостаток жира в организме сам по себе может иметь негативные последствия для здоровья, и поддержание процентного содержания жира в организме ниже или даже на уровне необходимого процентного содержания жира в организме — это тема, которую следует обсудить. обсуждается с медицинским работником.
Накопленный жир — это жир, который накапливается в жировой ткани, будь то подкожный жир (глубоко под дермой и обернутый вокруг жизненно важных органов) или висцеральный жир (жир, расположенный внутри брюшной полости, между органами), и ссылки на телесный жир обычно относятся к этому тип жира.Хотя немного жировых отложений является идеальным вариантом, их избыточное количество может иметь серьезные негативные последствия для здоровья.
Избыток жира в организме приводит к избыточному весу и, в конечном итоге, к ожирению, учитывая, что не принимаются достаточные меры для сдерживания увеличения жировых отложений. Обратите внимание, что лишний вес не обязательно указывает на избыток жира в организме. Масса тела человека складывается из множества факторов, включая (но не ограничиваясь) жировые отложения, мышцы, плотность костей и содержание воды.Таким образом, людей с высокой мускулатурой часто относят к категории полных.
Скорость накопления жира в организме у разных людей разная и зависит от многих факторов, включая генетические факторы, а также поведенческие факторы, такие как недостаток физических упражнений и чрезмерное потребление пищи. Из-за различных факторов некоторым людям может быть труднее уменьшить жировые отложения, накопленные в области живота. Однако было доказано, что соблюдение диеты и физических упражнений снижает накопленный жир. Обратите внимание, что и женщины, и мужчины накапливают жир по-разному, и это может измениться со временем.После 40 лет (или после менопаузы в некоторых случаях для женщин) снижение половых гормонов может привести к избытку жира в области живота у мужчин или вокруг ягодиц и бедер у женщин.
Возможные осложнения излишка жира в организме
Всемирная организация здравоохранения (ВОЗ) классифицирует ожирение как одну из основных предотвратимых причин смерти во всем мире, от которой, по оценкам, умирает от 111 909 до 365 000 смертей в год в США 1 Это вызывает растущую обеспокоенность, поскольку 36.По данным Центров по контролю и профилактике заболеваний, 5% взрослого населения США страдают ожирением. 2
Ожирение связано со снижением качества жизни, ухудшением психического здоровья, обструктивным апноэ во сне, а также с множеством основных причин смерти во всем мире, такими как сердечно-сосудистые заболевания, инсульт, некоторые виды рака и диабет. 2 Все эти потенциальные осложнения могут сокращать продолжительность жизни человека, и поэтому ожирение — это заболевание, которое изучается многими исследователями.
Как упоминалось ранее, жир производит ряд основных гормонов, влияющих на организм человека. Избыток или недостаток критических гормонов может иметь негативные последствия, мешающие нормальному функционированию организма. Кстати, исследования показали, что избыток жира в организме, особенно в области живота, нарушает нормальный баланс и функцию некоторых из этих гормонов. Кроме того, телесный жир, особенно висцеральный жир, играет роль в высвобождении специфических цитокинов, которые представляют собой широкую категорию белков, участвующих в передаче сигналов клеток, которые потенциально могут увеличивать риск сердечно-сосудистых заболеваний.Висцеральный жир также напрямую связан с более высоким уровнем холестерина липопротеинов низкой плотности (ЛПНП), более низким уровнем холестерина липопротеинов высокой плотности (ЛПВП) и резистентностью к инсулину. 3 Холестерин ЛПНП обычно называют «плохим холестерином», тогда как ЛПВП называют «хорошим холестерином». Высокий уровень холестерина ЛПНП может закупорить артерии и привести к осложнениям, включая сердечные приступы. Инсулинорезистентность включает клетки, не отвечающие должным образом на гормон инсулин, что может привести к высокому уровню сахара в крови и, в конечном итоге, к диабету 2 типа. 1 Как видно, избыток висцерального жира может иметь ощутимые негативные последствия для здоровья человека.
Измерение процентного содержания жира в организме
ВМС США Метод:
Для измерения жира в организме используется множество специальных методов. В приведенном выше калькуляторе используется метод, включающий уравнения, разработанные в Исследовательском центре военно-морского здравоохранения Ходждоном и Беккетом в 1984 году. Метод измерения соответствующих частей тела, а также конкретные используемые уравнения представлены ниже:
- Измерьте окружность талии испытуемого на горизонтальном уровне вокруг пупка для мужчин и на уровне наименьшей ширины для женщин.Убедитесь, что испытуемый не втягивает живот внутрь, чтобы получить точные измерения.
- Измерьте окружность шеи испытуемого, начиная ниже гортани, с лентой, спускающейся вниз к передней части. Испытуемый не должен расширять шею наружу.
- Только для женщин: Измерьте окружность бедер испытуемого по наибольшему горизонтальному размеру.
После получения этих измерений используйте следующие формулы для расчета оценки содержания жира в организме.Предусмотрены два уравнения, в одном используется обычная система США (USC), в которой используются дюймы, а в другом — Международная система единиц, в частности, единица измерения в сантиметрах:
Формула процентного содержания жира в организме (BFP) для мужчин:
| Единицы USC: | ||||||
| BFP = 86,010 × log 10 (живот-шея) — 70,041 × log 10 (высота) + 36,76 | ||||||
| SI, метрические единицы: | ||||||
|
Формула процентного содержания жира в организме (BFP) для женщин:
| Единицы USC: | ||||||
| BFP = 163,205 × log 10 (пояс + бедро-шея) — 97,684 × (log 10 (высота)) + 36,76 | ||||||
| SI, метрические единицы: | ||||||
|
Обратите внимание, что результаты этих расчетов являются приблизительными, поскольку они основаны на множестве различных предположений, чтобы сделать их максимально применимыми к как можно большему количеству людей. Для более точного измерения жира в организме необходимо использование таких инструментов, как анализ биоэлектрического импеданса или гидростатическое измерение плотности.
Формула массы жира (FM):
FM = BF × Вес
Формула сухой массы (LM):
LM = Вес — FM
Метод BMI:
Другой метод расчета процентного содержания жира в организме использует ИМТ. Обратитесь к калькулятору ИМТ, чтобы получить оценку ИМТ для использования с методом ИМТ, а также дополнительные сведения о том, как рассчитывается ИМТ, его значение и ограничения.Вкратце, оценка ИМТ включает использование формул, требующих измерения роста и веса человека. Учитывая ИМТ, следующие формулы можно использовать для оценки процентного содержания жира в организме человека.
Формула процентного содержания жира в организме (BFP) для взрослых мужчин:
BFP = 1,20 × ИМТ + 0,23 × Возраст — 16,2
Формула процентного содержания жира в организме (BFP) для взрослых женщин:
BFP = 1,20 × ИМТ + 0,23 × Возраст — 5,4
Формула процентного содержания жира в организме (BFP) для мальчиков:
BFP = 1.51 × ИМТ — 0,70 × Возраст — 2,2
Формула процентного содержания жира в организме (BFP) для девочек:
BFP = 1,51 × ИМТ — 0,70 × Возраст + 1,4
- Wikipedia.org
- «Избыточный вес и ожирение». Центры по контролю и профилактике заболеваний . www.cdc.gov/obesity/data/index.html
- «Абдоминальный жир и что с этим делать». Harvard Health Publishing: Гарвардская медицинская школа . www.health.harvard.edu/staying-healthy/abdominal-fat-and-what-to-do-about-it
.
Калькулятор площади поверхности тела
Калькулятор ниже вычисляет общую площадь поверхности человеческого тела, называемую площадью поверхности тела (BSA). Прямое измерение BSA затруднено, и поэтому было опубликовано множество формул для оценки BSA. Калькулятор ниже предоставляет результаты для некоторых из самых популярных формул.
Калькулятор Связанной Площади | Калькулятор площади поверхности
Таблица средних значений BSA
| футов 2 | м 2 | |
| Новорожденный | 2.69 | 0,25 |
| Двухлетний ребенок | 5,38 | 0,5 |
| Десятилетний ребенок | 12,27 | 1,14 |
| Взрослая женщина | 17,22 | 1,6 |
| Взрослый мужчина | 20,45 | 1,9 |
BSA часто используется в клинических целях по сравнению с массой тела, поскольку это более точный индикатор метаболической массы (потребности организма в энергии), где метаболическую массу можно оценить как жир -свободная масса, поскольку жировые отложения метаболически не активны. 1 BSA используется в различных клинических условиях, таких как определение сердечного индекса (чтобы связать работу сердца человека с размером его тела) или дозировки для химиотерапии (категория лечения рака). Хотя дозировка для химиотерапии часто определяется с использованием BSA пациента, существуют аргументы против использования BSA для определения дозировок лекарств с узким терапевтическим индексом — сравнение количества вещества, необходимого для оказания терапевтического эффекта, с количеством, которое вызывает токсичность.
Ниже приведены некоторые из наиболее популярных формул для оценки BSA и ссылки на ссылки по каждой из них для получения более подробной информации об их выводе. Наиболее широко используемой из них является формула Дюбуа, которая, в отличие от индекса массы тела, оказалась эффективной для оценки жировых отложений как у пациентов с ожирением, так и у пациентов без ожирения. Если BSA представлен в м 2 , W — это вес в кг , а H — это высота в см , формулы имеют следующий вид:
Формула Дюбуа:
BSA = 0.007184 × Ш 0,425 × В 0,725
Du Bois D, Du Bois EF (июнь 1916 г.). «Формула для оценки приблизительной площади поверхности, если известны рост и вес». Архив внутренней медицины 17 (6): 863-71. PMID 2520314. Проверено 9 сентября 2012 г.
Формула Мостеллера:
BSA = = 0,016667 × Ш 0,5 × В 0,5
Mosteller RD. «Упрощенный расчет площади поверхности тела». N Engl J Med 1987; 317: 1098. PMID 3657876.
Формула Хейкока:
BSA = 0,024265 × Ш 0,5378 × В 0,3964
Haycock GB, Schwartz GJ, Wisotsky DH «Геометрический метод измерения площади поверхности тела: формула роста и веса, проверенная на младенцах, детях и взрослых» J Pediatr 1978, 93: 62-66.
Формула Гехана и Джорджа:
BSA = 0,0235 × W 0,51456 × H 0,42246
Gehan EA, George SL, Cancer Chemother Rep 1970, 54: 225-235
Формула Бойда:
BSA = 0.03330 × Ш (0,6157 — 0,0188 × log10 (Ш) × В 0,3
Бойд, Эдит (1935). Рост площади поверхности человеческого тела. Университет Миннесоты. Институт защиты детей, серия монографий, № x. Лондон: Oxford University Press
Формула Фудзимото:
BSA = 0,008883 × Ш 0,444 × В 0,663
Фудзимото С., Ватанабэ Т., Сакамото А., Юкава К., Моримото К. Исследования площади физической поверхности японцев.18. Расчетные формулы в три этапа для всех возрастов. Nippon Eiseigaku Zasshi 1968; 5: 443-50.
Формула Такахира:
BSA = 0,007241 × Ш 0,425 × В 0,725
Фудзимото С., Ватанабэ Т., Сакамото А., Юкава К., Моримото К. Исследования площади физической поверхности японцев. 18. Расчетные формулы в три этапа для всех возрастов. Nippon Eiseigaku Zasshi 1968; 5: 443-50.
Формула Шлиха:
Женщины BSA = 0.000975482 × Ш 0,46 × В 1,08
Мужчины BSA = 0,000579479 × Ш 0,38 × В 1,24
Schlich E, Schumm M, Schlich M: «3D-сканирование тела als anthropometrisches Verfahren zur Bestimmung der spezifischen Korperoberflache». Эрнахрунгс Умшау 2010; 57: 178-183
1. Гринберг, JA., Boozer, CN. 1999. «Метаболическая масса, скорость метаболизма, ограничение калорийности и старение у самцов крыс Fischer 344». Elsevier 113 (2000): 37-48
.

