Х в кубе х 0: Решить уравнение x в кубе плюс x равно ноль
3+ 1$.
1. Составим таблицу значений:
2. Построим точки. Мы видим, что эти точки симметричны относительно точки с координатами (0,1). В итоге получаем кубическую параболу, смещенную вверх по оси OY (см. рис. 3).
- Президент Кубы призвал коммунистов выйти на улицы и отреагировать на «провокации»
- Ученые РФ изучат биоразнообразие Арктики в крупнейшей с 1990-х гг. экспедиции | 11.02.22
- От Loon до «Полярной звезды»
- Обучающие игрушки | kaup24.ee
- СПАРК — Проверка контрагента, узнать сведения об организации по ИНН, анализ рынка в системе СПАРК-Интерфакс
- Докажите, что х в кубе — 3х в квадрате у + 3xy в квадрате — y в кубе = (х
- Решение квадратных уравнений методом факторинга
- Выразите многочлен как произведение линейных коэффициентов
- Видео Вопрос: Нахождение множества нулей кубической функции
- — MathPapa
- Математическая сцена — Уравнения III- Урок 2
Президент Кубы призвал коммунистов выйти на улицы и отреагировать на «провокации»
США предостерегли власти Кубы от насилия в отношении протестующих кубинцев. Вашингтон также обеспокоен «призывами к оружию», исходящими от властей «острова свободы». Ранее на фоне пандемии COVID-19, проблем с подачей электричества и невиданной с 1990-х годов нехваткой еды на Кубе начались массовые, многотысячные протесты. Президент республики Мигель Диас-Канель уже назвал демонстрантов «наймитами империалистов из США».
Помощник президента США по нацбезопасности Джейк Салливан заявил, что американское руководство предостерегает власти Кубы от насильственного подавления акций протеста, начавшихся на острове. Об этом чиновник написал в своем Twitter.
«США поддерживают свободу выражения мнений и свободу собраний на Кубе и решительным образом осудят любое насилие или действия, направленные против мирных протестующих, которые отстаивают свои общечеловеческие права», — сказал Салливан.
Он также сообщил, что Вашингтон беспокоят «призывы к оружию» президента Кубы Мигеля Диаса-Канеля. Тот в своем воззвании ранее обратился ко «всем коммунистам и защитникам революции», заявив о необходимости «выйти на улицы Кубы и отреагировать на провокации».
Протесты против действующего руководства Кубы начались 11 июля на фоне роста заболеваемости COVID-19, перебоев с подачей электроэнергии и нехватки продовольствия в магазинах. В этот день в стране было отмечено рекордное количество новых случаев коронавируса. По данным французских СМИ,
демонстранты наводнили улицы Гаваны и других городов, выступая против коммунистической диктатуры. Среди их лозунгов — «Свободу», «Долой коммунизм», «Родина и жизнь» и призывы дать людям лекарства, еду и вакцину от коронавируса.
Cuba est gritando LIBERTAD!!!!! #SOSCuba pic.twitter.com/6Du4dp6WmR
— Yusnaby Prez (@Yusnaby) July 11, 2021
По данным кубинского гостелевидения, в некоторых городах произошли беспорядки, были разгромлены магазины — полки даже нетронутых магазинов остаются практически пустыми. На улицах Гаваны появились военные и полицейские автомобили с пулеметами. По словам президента Диас-Канеля, «власти не позволят контреволюционным наймитам, продавшимся империи американцев, устроить провокации и дестабилизацию ситуации».
На улицах Гаваны появились военные и полицейские автомобили с пулеметами. По словам президента Диас-Канеля, «власти не позволят контреволюционным наймитам, продавшимся империи американцев, устроить провокации и дестабилизацию ситуации».
Кроме того, глава Кубы заявил, что «это те янки, которые всегда поддерживали блокаду, требуют «гуманитарной интервенции» и сеют слухи, что правительство не справляется с эпидемией».
«Пока есть ром и сигары»
На Кубе наблюдается «тотальный дефицит», написал ранее в личном Telegram-канале главред издания Baza Никита Могутин, побывавший недавно на «острове свободы».
«Вы покидаете отель, но вас заранее просят: вы не могли бы перед отъездом оставить свои лекарства нам? Вы удивляетесь: ну зачем вам мои таблетки? А вам отвечают: «На Кубе очень тяжело достать лекарства, аптек мало и там маленький выбор, нет даже необходимых лекарств». Поэтому все русские передают по цепочке одну и ту же фразу: «Ребят, оставляйте лекарства в отелях местным – им реально нужно», — говорится в одном из его постов о ситуации на Кубе.
Проблемы на острове наблюдаются, по словам Могутина, и с продовольствием.
«Сидя в отеле на Кубе, ты жалуешься на скудную еду – рыба, тыква, курица, сосиски, рис. Ты приезжаешь в Гавану, заходишь в магазин, видишь зубные щетки и тебе снова становится стыдно. Можно, конечно, купить продукты на черном рынке – но нужны знакомые. Особенно тяжело, говорят, стало во время изоляции. Очень многие остались без средств к существованию, на улицах стало больше нищих и пьяных людей», — пишет журналист.
Практически везде, добавил он, наблюдается продуктовый дефицит. «Очереди – пожалуй, это первое, на что обращаешь внимание, когда выезжаешь за пределы курортных зон на Кубе. Очереди везде. Стоят в продовольственные и обувные, стоят за одеждой, иногда стоят просто так, – даже не зная, за чем именно», — отмечается в постах Могутина.
Сейчас на Кубе действует комендантский час — он наступает в 21:00 по местному времени. На улицах появляются военные патрули и полицейские блокпосты.
«Местные русские часто повторяют одну и ту же мантру: «Коммунисты держатся, пока есть ром и сигары». И добавляют: «Но скоро все изменится». Все уверены, что в стране полным ходом идет перестройка по российскому сценарию: все, что есть государственного – тайком раздадут ближнему кругу, откроют рынок и дадут людям повариться в собственном соку под чутким контролем силовиков», — сообщил также Могутин.
Новая экономическая модель
В апреле на Кубе сменилось руководство — о своем уходе в отставку объявил 89-летний Рауль Кастро. Его преемнику Мигелю Диас-Канелю досталась страна с ВВП, упавшим за минувший год на 11%. Кубинская экономика серьезно пострадала от введенных администрацией 45-го президента США Дональда Трампа экономических санкций — несмотря на некоторое потепление отношений при президенте Бараке Обаме.
Доцент экономического факультета РУДН Магомед Кодзоев ранее заявил «Газете.Ru», что повлияли на благосостояние Кубы не только санкции Трампа, но и пандемия коронавируса.
«Главный удар пришелся по туристической отрасли, второй статье доходов кубинского бюджета (после медицинского обслуживания). После учащения случаев заболеваний в конце прошлого года стало понятно, что пока Кубе рано открывать двери туризма», — отмечал он. Восстанавливаться отношения с США при Джо Байдене будут долго, предположил Кодзоев, но здесь дело в подходе демократов к Латинской Америке — Белый дом при Байдене не считает региональную тему приоритетной.
«По крайней мере, ужесточения санкционной политики в отношении Кубы можно не бояться», — отмечал эксперт в апреле.
Ученые РФ изучат биоразнообразие Арктики в крупнейшей с 1990-х гг. экспедиции | 11.02.22
Ученые четырех институтов СО РАН при поддержке «Норильского никеля» («Норникель») в 2022 году проведут впервые с 1990-х годов масштабные комплексные исследования биоразнообразия на территориях деятельности компании на Кольском полуострове, на севере Красноярского края и в Забайкальском крае. Об этом сообщил в пятницу в пресс-центре ТАСС руководитель проекта, директор Института систематики и экологии животных СО РАН Виктор Глупов.
Об этом сообщил в пятницу в пресс-центре ТАСС руководитель проекта, директор Института систематики и экологии животных СО РАН Виктор Глупов.
«Экология — наука, изучающая взаимоотношения в сообществах, и биоразнообразие — критерий сообщества, чем выше уровень биоразнообразия, тем стабильнее экосистема, это по сути индекс жизни. Мы с большой радостью приняли предложение «Норникеля» о проведении базовых исследований биоразнообразия. Это уникальнейшая экспедиция, которых после развала Советского Союза не было», — сказал Глупов.
Как уточнил на пресс-конференции вице-президент по экологии и промышленной безопасности ПАО «ГМК «Норильский никель» Станислав Селезнев, данные исследования беспрецедентны по масштабам и пройдут на территориях Норильского промышленного узла, Забайкалья, Кольского полуострова и Северного морского пути.
«Помимо традиционных инициатив по поддержке заповедников и производству рыб, «Норникель» будет планомерно выстраивать комплексную систему управления в области биоразнообразия в соответствии с ведущими международными стандартами, будут созданы программы по сохранению и мониторингу биоразнообразия. Я уверен, что эти исследования внесут весомый вклад в научную деятельность всей страны и лягут в основу корпоративной системы управления воздействия на биоразнообразие», — сказал он.
Я уверен, что эти исследования внесут весомый вклад в научную деятельность всей страны и лягут в основу корпоративной системы управления воздействия на биоразнообразие», — сказал он.
Глупов уточнил, что уникальность экспедиции заключается в том числе в ее комплексности — в последний раз комплексные исследования данных территорий проводились в начале 1990-х, но даже они не охватывали такой процент экосистем российской Арктики. Этап исследований, посвященный основам биоразнообразия, пройдет в течение 2022 года, к работе будут привлекаться от 30 до 60 зоологов, ихтиологов, гидробиологов, почвоведов и ботаников Института систематики и экологии животных, Института биофизики Федерального исследовательского центра «Красноярский научный центр», Центрального сибирского ботанического сада, а также института почвоведения и агрохимии СО РАН, а также приглашенных мировых и местных экспертов.
В 2020 году СО РАН впервые за последние годы направило на Таймыр по приглашению «Норникеля» большую научную экспедицию для масштабного изучения территории и оценки влияния разлива топлива на Норильской ТЭЦ-3 на окружающую среду. Проект получил название «Большая норильская экспедиция».
Проект получил название «Большая норильская экспедиция».
Информационное агентство России ТАСС
От Loon до «Полярной звезды»
Крылатую ракету Loon (полная копия V-1) американцы собирались использовать против Японии, но та капитулировала раньше, чем «Гагары» были подготовлены к применению. Затем на вооружение ВВС США поступила КРНБ MGM-1 «Матадор» с ядерной БЧ и дальностью стрельбы тысяча километров. В конце 50-х годов ее сменила MGM-13 «Мэйс» также в ядерном оснащении и с дальностью до 2,4 тысячи километров. В начале 70-х ее сняли с вооружения, линия развития КРНБ на некоторое время прервалась в пользу ракет баллистических. Для ВМС США на основе V-1 была создана КРМБ «Регулус», ее могли запускать как с ПЛ (но только из надводного положения), так и с надводных кораблей. Она несла ядерную БЧ, дальность стрельбы достигала 900 километров. В середине 60-х эти КРМБ были сняты с вооружения (также в пользу баллистических ракет).
На вооружение сухопутных войск США в 1953 году начала поступать неуправляемая баллистическая ракета Honest John с дальностью полета 25 километров, затем американцы увеличили дистанцию выстрела до 45 километров.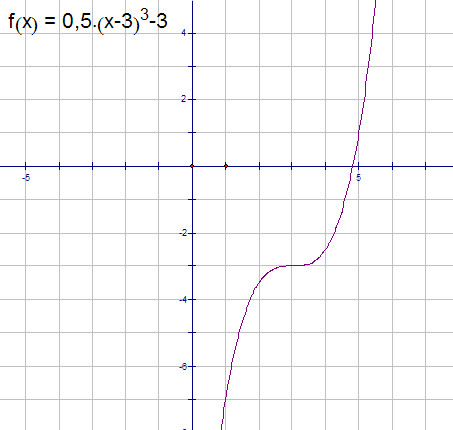 Ракета могла нести как ядерную, так и обычную БЧ, экспортировалась ближайшим союзникам США. Была она весьма примитивной, однако в Греции, Турции, Республике Корея «Честный Джон» состояла на вооружении до конца 90-х годов. Первой армейской управляемой БР стала MGM-5 «Капрал». Несла ядерную БЧ на дальность до 130 километров. В середине 60-х была заменена на MGM-29 «Сержант», которая могла использоваться и в обычном оснащении. В конце 70-х годов эту ракету сменила MGM-52 «Ланс», которая могла нести обычную БЧ на дальность 70–80 или ядерную на 110–120 километров. Состояла также на вооружении ВС Израиля и армий ряда стран НАТО. В США снята с вооружения в начале 90-х.
Ракета могла нести как ядерную, так и обычную БЧ, экспортировалась ближайшим союзникам США. Была она весьма примитивной, однако в Греции, Турции, Республике Корея «Честный Джон» состояла на вооружении до конца 90-х годов. Первой армейской управляемой БР стала MGM-5 «Капрал». Несла ядерную БЧ на дальность до 130 километров. В середине 60-х была заменена на MGM-29 «Сержант», которая могла использоваться и в обычном оснащении. В конце 70-х годов эту ракету сменила MGM-52 «Ланс», которая могла нести обычную БЧ на дальность 70–80 или ядерную на 110–120 километров. Состояла также на вооружении ВС Израиля и армий ряда стран НАТО. В США снята с вооружения в начале 90-х.
Практически все перечисленные ракеты, как крылатые, так и баллистические, после списания использовались в качестве мишеней для ПВО и ПРО США.
“ Высокоточное оружие широко применялось уже в ходе операции «Буря в пустыне», а начиная с интервенции в Ирак в 2003 году США по сути используют уже только вооружение высокой точности ”
Самую большую дальность среди армейских БВ США имела MGM-31А «Першинг-1А» – 740 километров. Несла ядерную БЧ. Состояла на вооружении с конца 60-х годов, в начале 90-х была уничтожена по ДРСМД.
Несла ядерную БЧ. Состояла на вооружении с конца 60-х годов, в начале 90-х была уничтожена по ДРСМД.
В конце 50-х годов в США были созданы две ядерные БРСД (дальность – 2400 километров) – PGM-17 «Тор» для ВВС и армейская PGM-19 «Юпитер». Их развертывание в Европе стало важнейшей причиной Карибского кризиса (СССР развернул аналогичное по назначению оружие на Кубе). После вывода советских ракет с Кубы как «Торы», так и «Юпитеры» были сняты с вооружения. Одной из причин отказа от них (кроме «размена» с СССР) стало принятие на вооружение гораздо более совершенных БРПЛ «Поларис», которые размещались на 41 американской ПЛАРБ и на четырех ПЛАРБ ВМС Великобритании (по 16 БРПЛ на ПЛАРБ). Всего было выпущено 509 моноблочных «Полярных звезд» А1/2 (дальность полета – 2,2–2,8 тыс. км), а затем 644 «Поларис» А3 (в том числе 133 для ВМС Великобритании) с дальностью 4600 километров и тремя БЧ по 200 килотонн. БРПЛ «Посейдон» имела ту же дальность, что и «Поларис» А3, но могла нести до 10 ядерных БЧ по 50 килотонн. «Посейдоны», которых выпущено 619, заменили «Поларисы» на 31 американской ПЛАРБ. Все эти ПЛАРБ (из которых 12 еще успели перевооружиться на «Трайдент-1») и оба типа БРПЛ были ликвидированы в конце 80-х – начале 90-х в соответствии с Договорами СНВ.
«Посейдоны», которых выпущено 619, заменили «Поларисы» на 31 американской ПЛАРБ. Все эти ПЛАРБ (из которых 12 еще успели перевооружиться на «Трайдент-1») и оба типа БРПЛ были ликвидированы в конце 80-х – начале 90-х в соответствии с Договорами СНВ.
В конце 50-х годов на вооружение ВВС США поступила первая ядерная моноблочная МБР «Атлас» (дальность – 10,2 тыс. км). Максимальное количество одновременно развернутых «Атласов» составляло 129 единиц, уже к середине 60-х их списали и переделали в ракеты-носители (РН) для космических запусков. Вместо них приняли на вооружение МБР LGM-25 «Титан» с дальностью полета 15 тысяч километров и БЧ мощностью 9 мегатонн. Одновременно развертывалось до 60 «Титанов», последние были сняты с вооружения в середине 80-х годов, некоторые были также использованы как РН, остальные уничтожены по Договору о СНВ.
После этого основными МБР наземного (шахтного, как у «Атласа» и «Титана») базирования стали «Минитмены». МБР LGM-30А/В «Минитмен-1» и LGM-30F «Минитмен-2» имели дальность полета 9–11 тысяч километров и несли ядерную БЧ мегатонного класса. КВО, как и у предыдущих МБР, составляла один – три километра. Было выпущено примерно 930 «Минитменов-1» (из них 385 использованы в испытательных пусках) и 668 «Минитменов-2» (использованы 189). Эти МБР сняты с вооружения в рамках СНВ, при этом в США делали попытки использовать первые ступени «Минитменов-2» для создания ракет системы ПРО. В 1970 году на вооружение поступил LGM-30G «Минитмен-3», дальность полета была повышена до 13 тысяч километров, КВО не превышало 500 метров, ракета несла три ядерные БЧ (170-475 кт). Было выпущено 830 «Минитменов-3», примерно 300 израсходовано в испытательных пусках. Максимальное количество одновременно развернутых «Минитменов» составляло 1000 (450 «Минитмен-2», 550 «Минитмен-3»), именно столько было построено шахт. В настоящее время на вооружении остается только «Минитмен-3», ракета прошла через множество модернизаций.
КВО, как и у предыдущих МБР, составляла один – три километра. Было выпущено примерно 930 «Минитменов-1» (из них 385 использованы в испытательных пусках) и 668 «Минитменов-2» (использованы 189). Эти МБР сняты с вооружения в рамках СНВ, при этом в США делали попытки использовать первые ступени «Минитменов-2» для создания ракет системы ПРО. В 1970 году на вооружение поступил LGM-30G «Минитмен-3», дальность полета была повышена до 13 тысяч километров, КВО не превышало 500 метров, ракета несла три ядерные БЧ (170-475 кт). Было выпущено 830 «Минитменов-3», примерно 300 израсходовано в испытательных пусках. Максимальное количество одновременно развернутых «Минитменов» составляло 1000 (450 «Минитмен-2», 550 «Минитмен-3»), именно столько было построено шахт. В настоящее время на вооружении остается только «Минитмен-3», ракета прошла через множество модернизаций.
Постепенное уменьшение размеров ракет, совершенствование двигателей, систем наведения, других компонентов привели к созданию различных классов этого оружия. Так, еще в 50-е годы появились первые противотанковые управляемые ракеты с кумулятивной БЧ. США долгое время отставали и вынуждены были использовать французские ПТУР. Лишь в 60-е создан американский ПТРК BGM-71 «Тоу» (TOW – Tube-launched Optically-tracked Wire-guided), оказавшийся весьма удачным. Как следует из приведенного английского названия, наведение ПТУР является оптическим полуавтоматическим, осуществляется по проводам. Дальность стрельбы составляет от 65 до 3750 метров. ПТРК «Тоу» прошел через множество модернизаций. Начиная с варианта BGM-71Е «Тоу-2А» ПТУР этого типа имеет тандемную БЧ для пробития активной и/или разнесенной брони. ПТРК «Тоу» применялся во множестве войн, до сих пор находится в производстве, общее количество произведенных ПТУР имеет шанс достичь миллиона единиц. Кроме переносной ПУ, может размещаться на джипах, БМП, БТР, вертолетах. В ряде стран «Тоу» выпускались по лицензии, в Иране производятся без лицензии (под названием «Туфан»). Почти одновременно с «Тоу» на вооружение был принят ПТРК FGM-77 «Дракон» с аналогичной системой наведения, но меньшей дальностью стрельбы (до километра), который применялся только в переносном варианте.
Так, еще в 50-е годы появились первые противотанковые управляемые ракеты с кумулятивной БЧ. США долгое время отставали и вынуждены были использовать французские ПТУР. Лишь в 60-е создан американский ПТРК BGM-71 «Тоу» (TOW – Tube-launched Optically-tracked Wire-guided), оказавшийся весьма удачным. Как следует из приведенного английского названия, наведение ПТУР является оптическим полуавтоматическим, осуществляется по проводам. Дальность стрельбы составляет от 65 до 3750 метров. ПТРК «Тоу» прошел через множество модернизаций. Начиная с варианта BGM-71Е «Тоу-2А» ПТУР этого типа имеет тандемную БЧ для пробития активной и/или разнесенной брони. ПТРК «Тоу» применялся во множестве войн, до сих пор находится в производстве, общее количество произведенных ПТУР имеет шанс достичь миллиона единиц. Кроме переносной ПУ, может размещаться на джипах, БМП, БТР, вертолетах. В ряде стран «Тоу» выпускались по лицензии, в Иране производятся без лицензии (под названием «Туфан»). Почти одновременно с «Тоу» на вооружение был принят ПТРК FGM-77 «Дракон» с аналогичной системой наведения, но меньшей дальностью стрельбы (до километра), который применялся только в переносном варианте. В настоящее время в США ПТРК «Дракон» практически снят с вооружения.
В настоящее время в США ПТРК «Дракон» практически снят с вооружения.
В конце 70-х – начале 80-х годов на вооружение поступила ПКР «Гарпун» (AGM-84 – в авиационном варианте, RGM-84 – в корабельном, UGM-84 – при запуске с ПЛ). Ракета имеет активную радиолокационную ГСН, дальность составляет 150 километров (в модификации D – 220 км).
В начале 80-х годов на вооружение ВС США поступили КР большой дальности с системой наведения TERCOM (по заранее заложенным цифровым картам местности), которая на поздних модификациях дополнена коррекцией по сигналам навигационной системы GPS. Эти ракеты были способны лететь к цели на предельно малой высоте (с огибанием рельефа), при этом имели крайне низкую ЭПР. Сочетание обоих факторов делало для ПВО противника крайне сложной задачей обнаружение КР, а большая дальность полета обеспечивала практически полную безопасность для их носителей. Основным недостатком является дозвуковая скорость полета, поэтому на максимальную дальность им нужно лететь два-три часа. При этом нет никаких средств противодействия ПВО, кроме малой заметности.
При этом нет никаких средств противодействия ПВО, кроме малой заметности.
На вооружение ВВС поступила КРВБ AGM-86 ALCM, в ядерном варианте она имеет дальность полета 2,4 тысячи километров и 1,2 тысячи – в обычном снаряжении («Удар «Гремучей змеи»). «Родственной» ракетной морского и наземного базирования стала КР BGM-109 «Томагавк» с теми же, что у AGM-86, дальностью полета и системой наведения. Ядерных ракет BGM-109G «Грифон» в наземном варианте было выпущено до 560 единиц, все они ликвидированы по ДРСМД. КРМБ «Томагавк», запускаемые с ПЛА, крейсеров и эсминцев, были изначально созданы в трех вариантах: А – в ядерном снаряжении, В (она же TSAM) – ПКР (активное радиолокационное наведение, дальность полета – 450 км), С (она же TLAM) – с обычной БЧ для поражения наземных целей. Всего было выпущено примерно четыре тысячи КРМБ трех вариантов. Позже появилась КРМБ BGM-109D с кассетной БЧ, а почти все КРМБ вариантов А и В переделали в модификации С и D.
В начале ХХI века на вооружение поступили КРМБ BGM-109Е «Тактический Томагавк», коих уже произведено более четырех тысяч единиц. Около 200 «Томагавков», в том числе 65 «Тактических Томагавков», получили ВМС Великобритании (применяются только с ПЛА). В ходе различных военных кампаний израсходовано не менее 2,3 тысячи «Томагавков». Соответственно сейчас ВМС США могут иметь до двух тысяч BGM-109A/B/C/D и около четырех тысяч BGM-109Е. Именно эти КРМБ, а не авианосная авиация, являются главной ударной силой американского флота.
Около 200 «Томагавков», в том числе 65 «Тактических Томагавков», получили ВМС Великобритании (применяются только с ПЛА). В ходе различных военных кампаний израсходовано не менее 2,3 тысячи «Томагавков». Соответственно сейчас ВМС США могут иметь до двух тысяч BGM-109A/B/C/D и около четырех тысяч BGM-109Е. Именно эти КРМБ, а не авианосная авиация, являются главной ударной силой американского флота.
Кроме ОТР «Першинг-1А» и КРНБ BGM-109G «Грифон», жертвой ДРСМД стала ядерная БРСД MGM-31С «Першинг-2», имевшая дальность полета около 1,8 тысячи километров и очень высокую точность (КВО составляло всего 30 метров). Были произведены 384 такие ракеты. После их ликвидации единственной американской нестратегической БР наземного базирования остается MGM-140 АТАСМS, принятая на вооружение в начале 90-х (заменила «Ланс»). Она несет кассетную БЧ на дальность 150–300 километров, наведение корректируется по GPS. ПУ для нее являются РСЗО М270 MLRS (1 или 2 ATACMS на ПУ) или М142 HIMARS (1 ATACMS на ПУ).
Наиболее современной американской МБР стала LGM-118А «Миротворец», более известная, как МХ. Была принята на вооружение в конце 80-х, несла до 10 БЧ по 300 килотонн на дальность 9,6 тысячи километров, при этом КВО не превышало 90 метров. Было выпущено 114 таких МБР, одновременно развертывалось 50. В испытательных запусках израсходована как минимум 51 МБР. По Договору СНВ-2 данная МБР была снята с вооружения, ее БЧ частично переставлены на «Минитмены-3». Сами ракеты переделываются в космические РН «Минотавр» (на данный момент произведено не менее шести запусков этих ракет).
Основу СЯС США по-прежнему составляют БРПЛ и их ядерные БЧ. UGM-96 «Трайдент-1» несла шесть БЧ по 100 килотонн на дальность 7,4 тысячи километров (при меньшей дальности могла нести до 14 БЧ). Устанавливалась вместо «Посейдонов» на 12 ПЛАРБ ранних серий, а также на первых 8 ПЛАРБ типа «Огайо» (по 24 БРПЛ на каждой ПЛАРБ). Было произведено 595 БРПЛ, из них 168 использованы при испытательных пусках. В начале ХХI века были сняты с вооружения и полностью заменены на БРПЛ UGM-133А «Трайдент-2», которые начали поступать на вооружение ПЛАРБ типа «Огайо» с начала 90-х. Эта БРПЛ способна нести от 8 до 14 ядерных БЧ при КВО не более 120 метров, дальность полета может достигать 11,3 тысячи километров. Изготовлено не менее 857 «Трайдентов-2», в том числе 72 для Великобритании (на замену «Поларисам»). Как минимум 186 БРПЛ израсходовано в ходе испытательных пусков, соответственно ВМС США в настоящее время могут иметь около 600 «Трайдентов-2», из которых одновременно могут быть развернуты до 288.
Эта БРПЛ способна нести от 8 до 14 ядерных БЧ при КВО не более 120 метров, дальность полета может достигать 11,3 тысячи километров. Изготовлено не менее 857 «Трайдентов-2», в том числе 72 для Великобритании (на замену «Поларисам»). Как минимум 186 БРПЛ израсходовано в ходе испытательных пусков, соответственно ВМС США в настоящее время могут иметь около 600 «Трайдентов-2», из которых одновременно могут быть развернуты до 288.
Поскольку СЯС остаются «оружием Судного дня», которое неприменимо в обычных войнах, в Штатах активно совершенствуется неядерное ракетное оружие. При этом основной тенденцией его развития стало максимальное повышение точности, которое должно обеспечить поражение цели первым же боеприпасом. Подобное оружие широко применялось уже в ходе операции «Буря в пустыне», а начиная с интервенции в Ирак в 2003 году США по сути используют уже только высокоточное оружие. В первую очередь, впрочем, оно является авиационным. Пример наземного высокоточного оружия – принятый на вооружение в середине 90-х годов ПТРК FGM-148 «Джавелин» с инфракрасной ГСН. Имеет тандемную кумулятивную БЧ, после пуска совершает «горку» и поражает цель в менее защищенную верхнюю полусферу. Дальность стрельбы – до трех километров.
Имеет тандемную кумулятивную БЧ, после пуска совершает «горку» и поражает цель в менее защищенную верхнюю полусферу. Дальность стрельбы – до трех километров.
В связи с тем, что ВС США от «борьбы с международным терроризмом» вновь переориентируются на борьбу с равными по силам противниками (Россией и Китаем), значение такого оружия для них еще более возрастет. Будут активно разрабатываться ракеты большой дальности различных классов, обеспечивающие подавление и/или преодоление мощной ПВО и поражение широкого спектра целей, в том числе наиболее сложных. Ведутся работы по программе Precision Strike Missile (PrSM) с целью создания ОТР дальностью до 700 километров для замены АТАСМS. Причем этих новых ракет на ПУ должно размещаться вдвое больше, то есть четыре на М270 и две на HIMARS. Универсальной гиперзвуковой ракетой может стать С-НGB с дальностью две – четыре тысячи километров. Ее планируют использоваться как полезная нагрузка наземной системы Long Range Hypersonic Weapon (LRHW), батарея этой системы будет включать четыре ПУ, по две БРСД на каждой. Возможно, эту систему создадут и в морском варианте для ПЛА типа «Вирджиния». Судьба еще нескольких перспективных ракетных проектов ВС США пока неясна.
Возможно, эту систему создадут и в морском варианте для ПЛА типа «Вирджиния». Судьба еще нескольких перспективных ракетных проектов ВС США пока неясна.
Обучающие игрушки | kaup24.ee
Обучающие игрушки
Очень приятно и полезно, когда игрушки развивают определенные навыки ребенка, стимулируют воображение, творческие способности и имеют больше возможностей во время игры, пользуясь игрушкой. Игрушка является более ценной, если во время игры, увеличивается возможность применения ума ребенка, физической моторики и использования его творческого потенциала. Развивающие игрушки обычно изготавливаются из экологических материалов, с виду это простые и ничем не выделяющиеся игрушки, но они очень важные потому, что поощряют творческие способности ребенка. В этом и есть зацепка, которая помогает самим детям создавать нечто интересное.
Интернет магазин Kaup24.ee предлагает дешевле очень широкий выбор развивающих игрушек для детей разного возраста. Выбирая игрушку, надо обратить внимание на интересы ребенка, что ему больше нравится — лепить, рисовать, клеить, конструировать. Для детей младшего возраста предлагаем игрушки, которые помогают развивать творческие способности, и дают возможность создавать разные истории. Моделированная лепка или творческие наборы, позволяющие клеить веселые животные, разнообразные фигуры и пр. из наклеек для этого возраста, помогают развивать воображение ребенка. Для детей 3 – 7 лет предлагаем пазлы, мозаики, конструкторы, логические игры, наборы для творческого развития ребенка. Также, основными развивающими играми данного периода являются пластилин, карандаши, цветная бумага и ножницы. Детям дошкольного возраста очень нравятся конструкторы. Конструктор – это необходимый строительный материал для творческой игры ребенка.
Выбирая игрушку, надо обратить внимание на интересы ребенка, что ему больше нравится — лепить, рисовать, клеить, конструировать. Для детей младшего возраста предлагаем игрушки, которые помогают развивать творческие способности, и дают возможность создавать разные истории. Моделированная лепка или творческие наборы, позволяющие клеить веселые животные, разнообразные фигуры и пр. из наклеек для этого возраста, помогают развивать воображение ребенка. Для детей 3 – 7 лет предлагаем пазлы, мозаики, конструкторы, логические игры, наборы для творческого развития ребенка. Также, основными развивающими играми данного периода являются пластилин, карандаши, цветная бумага и ножницы. Детям дошкольного возраста очень нравятся конструкторы. Конструктор – это необходимый строительный материал для творческой игры ребенка. Конструкторы незаменимые и для развития мышления, интеллекта, воображения и творческих способностей. Кроме всего этого, конструкторы, помогают формировать такие свойства, как умение сконцентрироваться, общению с партнером, и главное быть уверенным в себя. Не менее важная цель конструктора – научить детей терпению и трудоспособности. Конструирование это и игра, и работа. Во время игры у ребенка формируется понятие формы, размера, связи пространственных предметов.
Конструкторы незаменимые и для развития мышления, интеллекта, воображения и творческих способностей. Кроме всего этого, конструкторы, помогают формировать такие свойства, как умение сконцентрироваться, общению с партнером, и главное быть уверенным в себя. Не менее важная цель конструктора – научить детей терпению и трудоспособности. Конструирование это и игра, и работа. Во время игры у ребенка формируется понятие формы, размера, связи пространственных предметов.
При выборе игрушки не забывайте про интересы вашего ребенка. Следует подчеркнуть, что в данное время развивающие игрушки составляют очень большой ассортимент и почти все соответствуют определенным требованиям. И так, остается только дополнить, что если вы хотите пополнить корзинку детских игрушек вашего ребенка развивающими игрушками, точно назовите интересы и выбирайте игрушки, соответствующие интересам вашего ребенка. Зачем это делать? Все очень просто – если игрушка будет соответствовать интересам ребенка, она еще больше возбудит его заинтересованность. Закажите по интернету игрушки прямо сейчас! У нас часто проходят разнообразные акции, поэтому заплатите самую низкую цену!
Закажите по интернету игрушки прямо сейчас! У нас часто проходят разнообразные акции, поэтому заплатите самую низкую цену!
СПАРК — Проверка контрагента, узнать сведения об организации по ИНН, анализ рынка в системе СПАРК-Интерфакс
| 1 |
Москва | 134,15 | 81 790 650,20 | 33,32 % | |
| 2 |
Санкт-Петербург | 91,82 | 21 966 175,41 | 8,95 % | |
| 3 |
Московская область | 91,34 | 17 507 467,77 | 7,13 % | |
| 4 |
Тюменская область | 141,29 | 10 731 908,63 | 4,37 % | |
| 5 |
Краснодарский край | 63,93 | 6 982 851,96 | 2,84 % | |
| 6 |
Свердловская область | 55,70 | 6 544 378,94 | 2,67 % | |
| 7 |
Республика Татарстан | 57,01 | 5 912 056,28 | 2,41 % | |
| 8 |
Нижегородская область | 66,63 | 5 108 443,77 | 2,08 % | |
| 9 |
Красноярский край | 75,79 | 4 602 145,74 | 1,87 % | |
| 10 |
Самарская область | 51,39 | 4 555 909,94 | 1,86 % | |
| 11 |
Башкортостан (Республика) | 54,74 | 4 143 430,64 | 1,69 % | |
| 12 |
Ростовская область | 50,42 | 3 706 578,69 | 1,51 % | |
| 13 |
Кемеровская область | 97,45 | 3 559 172,22 | 1,45 % | |
| 14 |
Челябинская область | 47,14 | 3 516 332,30 | 1,43 % | |
| 15 |
Новосибирская область | 35,84 | 3 401 496,76 | 1,39 % | |
| 16 |
Пермский край | 50,19 | 2 862 888,77 | 1,17 % | |
| 17 |
Приморский край | 48,74 | 2 578 156,83 | 1,05 % | |
| 18 |
Иркутская область | 51,45 | 2 551 634,44 | 1,04 % | |
| 19 |
Воронежская область | 52,35 | 2 345 212,33 | 0,96 % | |
| 20 |
Ленинградская область | 70,54 | 2 302 998,03 | 0,94 % | |
| 21 |
Белгородская область | 76,66 | 2 276 358,24 | 0,93 % | |
| 22 |
Калининградская область | 54,25 | 1 942 842,15 | 0,79 % | |
| 23 |
Вологодская область | 52,38 | 1 749 852,03 | 0,71 % | |
| 24 |
Хабаровский край | 49,13 | 1 660 687,74 | 0,68 % | |
| 25 |
Калужская область | 72,14 | 1 615 457,73 | 0,66 % | |
| 26 |
Волгоградская область | 42,42 | 1 464 757,15 | 0,60 % | |
| 27 |
Ярославская область | 43,31 | 1 439 430,46 | 0,59 % | |
| 28 |
Алтайский край | 32,26 | 1 430 455,77 | 0,58 % | |
| 29 |
Ставропольский край | 40,13 | 1 422 899,05 | 0,58 % | |
| 30 |
Оренбургская область | 49,78 | 1 406 729,61 | 0,57 % | |
| 31 |
Саратовская область | 34,80 | 1 400 069,26 | 0,57 % | |
| 32 |
Липецкая область | 72,20 | 1 374 978,35 | 0,56 % | |
| 33 |
Удмуртская Республика | 41,31 | 1 374 187,91 | 0,56 % | |
| 34 |
Тульская область | 51,16 | 1 364 418,82 | 0,56 % | |
| 35 |
Томская область | 50,40 | 1 293 777,11 | 0,53 % | |
| 36 |
Владимирская область | 46,36 | 1 227 037,27 | 0,50 % | |
| 37 |
Мурманская область | 88,47 | 1 212 648,17 | 0,49 % | |
| 38 |
Омская область | 30,93 | 1 135 973,43 | 0,46 % | |
| 39 |
Саха (Республика) (Якутия) | 50,29 | 1 072 922,52 | 0,44 % | |
| 40 |
Коми (Республика) | 67,63 | 1 021 277,56 | 0,42 % | |
| 41 |
Рязанская область | 40,83 | 976 300,88 | 0,40 % | |
| 42 |
Тверская область | 33,99 | 962 786,05 | 0,39 % | |
| 43 |
Смоленская область | 40,55 | 957 554,23 | 0,39 % | |
| 44 |
Курская область | 52,17 | 924 692,72 | 0,38 % | |
| 45 |
Кабардино-Балкарская Республика | 90,92 | 900 663,54 | 0,37 % | |
| 46 |
Пензенская область | 36,16 | 770 981,00 | 0,31 % | |
| 47 |
Тамбовская область | 52,61 | 744 194,46 | 0,30 % | |
| 48 |
Кировская область | 26,73 | 740 951,77 | 0,30 % | |
| 49 |
Брянская область | 44,82 | 723 485,40 | 0,29 % | |
| 50 |
Ульяновская область | 31,12 | 720 926,67 | 0,29 % | |
| 51 |
Республика Крым | 22,41 | 694 382,85 | 0,28 % | |
| 52 |
Сахалинская область | 48,83 | 653 304,08 | 0,27 % | |
| 53 |
Архангельская область | 33,54 | 649 333,35 | 0,26 % | |
| 54 |
Ивановская область | 23,93 | 615 981,93 | 0,25 % | |
| 55 |
Чувашская Республика-Чувашия | 29,30 | 584 117,98 | 0,24 % | |
| 56 |
Амурская область | 42,41 | 571 451,56 | 0,23 % | |
| 57 |
Астраханская область | 39,63 | 508 055,20 | 0,21 % | |
| 58 |
Дагестан (Республика) | 16,79 | 491 514,98 | 0,20 % | |
| 59 |
Новгородская область | 44,42 | 485 394,55 | 0,20 % | |
| 60 |
Орловская область | 39,88 | 474 230,56 | 0,19 % | |
| 61 |
Мордовия (Республика) | 41,12 | 473 335,20 | 0,19 % | |
| 62 |
Карелия (Республика) | 24,90 | 457 107,43 | 0,19 % | |
| 63 |
Бурятия (Республика) | 22,21 | 436 127,23 | 0,18 % | |
| 64 |
Магаданская область | 113,14 | 433 443,68 | 0,18 % | |
| 65 |
Камчатский край | 45,46 | 423 624,64 | 0,17 % | |
| 66 |
Марий Эл (Республика) | 36,26 | 400 294,82 | 0,16 % | |
| 67 |
Псковская область | 33,72 | 397 313,30 | 0,16 % | |
| 68 |
Забайкальский край | 29,53 | 373 109,88 | 0,15 % | |
| 69 |
Костромская область | 26,00 | 339 066,17 | 0,14 % | |
| 70 |
Курганская область | 27,01 | 310 943,06 | 0,13 % | |
| 71 |
Хакасия (Республика) | 39,49 | 303 267,57 | 0,12 % | |
| 72 |
Чеченская Республика | 22,61 | 224 494,95 | 0,09 % | |
| 73 |
Севастополь | 18,35 | 195 965,46 | 0,08 % | |
| 74 |
Карачаево-Черкесская Республика | 32,06 | 184 881,47 | 0,08 % | |
| 75 |
Чукотский автономный округ | 149,17 | 163 039,91 | 0,07 % | |
| 76 |
Северная Осетия-Алания (Республика) | 17,94 | 157 057,85 | 0,06 % | |
| 77 |
Алтай (Республика) | 31,24 | 151 552,92 | 0,06 % | |
| 78 |
Адыгея (Республика) (Адыгея) | 23,69 | 144 104,55 | 0,06 % | |
| 79 |
Тыва (Республика) | 14,27 | 50 890,17 | 0,02 % | |
| 80 |
Калмыкия (Республика) | 14,55 | 50 805,52 | 0,02 % | |
| 81 |
Еврейская автономная область | 18,69 | 43 913,11 | 0,02 % | |
| 82 |
Ингушетия (Республика) | 8,60 | 43 447,69 | 0,02 % |
Докажите, что х в кубе — 3х в квадрате у + 3xy в квадрате — y в кубе = (х
Другие вопросы по Алгебре
Решите уравнение: а)4 в степени х = 1/16 б)7 в степени х = 1/343 в)(1/6) в степени х = 36 г)0,2 в степени х = 0,00032. 3, если a = -1 1\8, b = 1 1\2…
3, если a = -1 1\8, b = 1 1\2…
Алгебра
08.03.2019 16:10
Чтобы добраться домой с дачи автомобилисту нужно было преодолеть путь длиной 240 км. когда автомобилист проехал половину пути, он понял, что не успевает в срок и увеличил скорость…
Алгебра
08.03.2019 23:20
Многолетняя проверка показала, что всхожесть семян огурцов определенного сорта составляет 90%.посеяли 200 семян. какое число проросших семян следует ожидать?…
Алгебра
10.03.2019 00:20
Для приготовления одного литра апельсинового сока требуется m кг. апельсин. сколько граммов апельсин требуется для приготовления 200 мл. апельсинового сока? (1 литр= 1000мл)…
Алгебра
10.03.2019 03:20
Последовательность b(n)- прогрессия. найдите сумму первых пяти ее членов, если b3=8, b4=16….
Алгебра
10.03.2019 10:40
5(3х-2)-4(7-2х)=6х (1+5х)(5х-1)-10(х-2)=19…
Алгебра
10. 2 > x(x+10) №3 з…
2 > x(x+10) №3 з…
Алгебра
11.03.2019 19:50
Товарному поезду до города необходимо проехать 72 км. отправление поезда задержалось на 4 ч. чтобы приехать в город вовремя, скорость поезда увеличили на 9 км/ч. какой должна была…
Алгебра
11.03.2019 21:04
Найти число, 12% которого равны 240…
Алгебра
12.03.2019 04:00
3 «.
Шаг за шагом Решение:
Шаг 1:
Шаг 2:
Вытягивание подобного Условия:
2.1 Вытащить как факторы:
x 3 — x = x • (x 2 — 1)
Пытаться к фактору как разница квадратов:
2.2 Факторинг: x 2 — 1
Теория: Разница двух идеальных квадратов, 2 — B 2 разложить на (A+B)•(AB)
Доказательство : (A+B)• (AB) =
A 2 — AB + BA — B 2 =
A 2 =
+ 0 — AB 2 B 2 =
A 2 — B 2Примечание: AB = BA является коммутативным свойством умножения.

Примечание. — AB + AB равно нулю и поэтому исключается из выражения.
Проверка: 1 – квадрат 1
Проверка : x 2 – квадрат x 1Факторизация: (x + 1) • (x — 1) шаг в конце уравнения
900 2 :х • (х + 1) • (х - 1) = 0Шаг 3 :
Теория – корни произведения:
3.1 Произведение нескольких членов равно нулю.
Если произведение двух или более слагаемых равно нулю, то хотя бы одно из слагаемых должно быть равно нулю.
Теперь мы будем решать каждый термин = 0 отдельно
Другими словами, мы собираемся решить столько уравнений, сколько членов в произведении
Любое решение термина = 0 также решает произведение = 0.
Уравнение одного переменного уравнения:
3.2 Решить: x = 0
Раствор представляет собой X = 0
Уравнение одного переменного уравнения:
3.3 Решить: X + 1 = 0
Вычтите 1 с обеих сторон уравнения :
x = -1Решение уравнения с одной переменной :
3.
3-7x-6= 0 | Wyzant Спросите эксперта
К сожалению, для разложения кубического многочлена на множители не существует простого правила «подключи и пыхни». Единственное, что мы можем сказать для 90 125 любого полинома 90 126, это то, что если x=r является корнем полиномиального выражения, одним из его множителей будет (x-r). Когда мы имеем дело с кубическим уравнением, мы ожидаем три корня — назовем их r 1 , r 2 и r 3 .
Это может показаться произвольным (потому что это так), но один из самых быстрых способов найти корни — это просто угадать и проверить простые значения.Я попробую 0, 1, 2 и 3:
f(x)= x 3 -7x-6
f(0)= 0 3 -7*0-6 = 0-0-6 = -6 x=0 не является корнем, поэтому (x-0)=x не является множителем.
f(1)= 1 3 -7*1-6 = 1-7-6 = -12 x=1 не является корнем, поэтому (x-1) не является множителем.

f(2)= 2 3 -7*2-6 = 8-14-6 = -12 x=2 не является корнем, поэтому (x-2) не является множителем.
f(3)= 3 3 -7*3-6 = 27-21-6 = 0 x=3 — корень, поэтому (x-3) — множитель.
Мы знаем, что x 3 -7x-6 делит на что-то похожее на (x-3)(……..). Отсюда у нас есть два варианта:
- Выполните полиномиальное деление, чтобы выяснить, что осталось: (…….)=(x 3 -7x-6)/(x-3). Однако полиномиальное деление запутано, и если бы мы могли избежать этого, было бы неплохо.
- Продолжайте гадать, чтобы найти больше корней!
Мы нашли несколько корней, соответствующих положительному x, поэтому давайте посмотрим в другую сторону:
f(-1)= (-1) 3 -7*(-1)-6 = -1+7-6 = 0 x=-1 — корень.(x+1) является фактором.
f(-2)= (-2) 3 -7*(-2)-6 = -8+14-6 = 0 x=-2 — корень.
(x+2) является фактором.
Нам повезло, и угадывание и проверка нашли корни довольно быстро. Мы заключаем, что x 3 -7x-6=(x-3)(x+2)(x+1) .
Просто ради этого перемножьте факторизованный многочлен еще раз, чтобы убедиться, что мы получили приемлемый ответ.
(х-3)(х+2)(х+1)
(х 2 +2х-3х-6)(х+1)
(х 2 -х-6)(х+1)
(х 2 -х-6)х + (х 2 -х-6)1
x 3 -x 2 -6x+x 2 -x-6
x 3 -7x-6
Решение квадратных уравнений методом факторинга
Пурпурная математика
Этот урок охватывает множество способов решения квадратных уравнений, таких как извлечение квадратных корней, завершение квадрата и использование формулы квадратного уравнения.
Но начнем мы с решения факторингом.
(Прежде чем перейти к решению квадратных уравнений, вы должны уже знать, как разложить квадратные выражения на множители. Если нет, сначала просмотрите, как разложить квадратные уравнения на множители.)
Вы уже разобрали квадратные выражения. Новым здесь является то, что квадратное выражение является частью уравнения, и вам предлагается найти значения переменной, которые делают уравнение верным. Вот как это работает:
Справка по математике.ком
Решите (
x – 3)( x – 4) = 0 с помощью факторизации.

Хорошо, этот квадрат уже учтен для меня.Но как мне использовать эту факторизацию для решения уравнения?
Для решения квадратичных уравнений с помощью факторизации мы используем то, что называется «Свойство нулевого произведения». Это свойство говорит о чем-то, что кажется довольно очевидным, но только после того, как нам на него укажут; а именно:
Свойство нулевого произведения: если мы умножаем две (или более) вещи вместе и результат равен нулю, то мы знаем, что по крайней мере одна из тех вещей, которые мы умножили, также должна быть равна нулю.Иными словами, единственный способ получить ноль при умножении двух (или более) множителей — это сделать так, чтобы один из множителей был равен нулю.
Итак, если мы умножаем два (или более) множителя и получаем нулевой результат, то мы знаем, что хотя бы один из множителей сам был равен нулю. В частности, мы можем положить каждый из сомножителей равным нулю, а полученное уравнение решить за одно решение исходного уравнения.
В частности, мы можем положить каждый из сомножителей равным нулю, а полученное уравнение решить за одно решение исходного уравнения.
Мы можем сделать полезный вывод о множителях (а именно, что один из этих множителей должен быть равен нулю, поэтому мы можем установить множители равными нулю), если само произведение равно нулю.Если произведение факторов равно любому ненулевому, то мы не можем сделать любого утверждения о значениях факторов.
Следовательно, при решении квадратных уравнений с помощью факторизации мы должны всегда иметь уравнение в форме «(квадратичное выражение) равно (нулю)», прежде чем мы попытаемся решить квадратное уравнение с помощью факторизации.
Возврат к упражнению:
Принцип нулевого фактора говорит мне, что по крайней мере один из факторов должен быть равен нулю.Так как хотя бы один из множителей должен быть равен нулю, то я могу установить каждых множителей равными нулю:
x – 3 = 0 или x – 4 = 0
Это дает мне простые линейные уравнения, и их легко решить:
И эти два значения являются решением, которое они ищут:
Обратите внимание, что « x = 3, 4″ означает то же самое, что и « x = 3 или x = 4″; разница только в форматировании. Формат « x = 3, 4″ является более распространенным.
Формат « x = 3, 4″ является более распространенным.
Решите
x 2 + 5 x + 6 = 0 и проверьте.
Это уравнение уже имеет вид «(квадратичное) равно (нулю)», но, в отличие от предыдущего примера, оно еще не разложено на множители. Сначала я ДОЛЖЕН факторизовать квадратное число, потому что только когда я УМНОЖАЮ и получаю ноль, я могу что-то сказать о множителях и решениях.Я не могу сделать вывод об отдельных членах нефакторизованного квадратичного числа (например, 5 90 265 x 90 266 или 6), потому что я могу добавить много вещей, которые в сумме равны нулю.
Итак, первое, что я должен сделать, это фактор:
x 2 + 5 x + 6 = ( x + 2)( x + 3)
Теперь я могу переформулировать исходное уравнение в терминах произведения множителей, причем это произведение равно нулю:
Теперь я могу найти каждый множитель, приравняв каждый из них к нулю и решив получившиеся линейные уравнения:
x + 2 = 0 или x + 3 = 0
x = –2 или x = – 3
Эти два значения являются решением исходного квадратного уравнения. Так что мой ответ:
Так что мой ответ:
Однако я еще не закончил, потому что в исходном упражнении мне было сказано «проверить», а это значит, что мне нужно подставить свои ответы обратно в исходное уравнение и убедиться, что оно получается правильным. В этом случае я подставлю выражение в левой части исходного уравнения и проверю, что в итоге получу правую часть; а именно с 0:
проверка x = –3:
[–3] 2 + 5[–3] + 6
9 – 15 + 6
9 + 6 – 15
15 – 15
0
проверка x = –2:
[–2] 2 + 5[–2] + 6
4 – 10 + 6
4 + 6 – 10
10 – 10
0
Когда в упражнении указано, что вы должны решить «и проверить» вышеприведенное упражнение «подключи и пыхни», они ищут вас, чтобы показать, что вы подключили свой ответ к исходному упражнению и получили правильное решение. Выше, где я показал свои чеки, это все, что им нужно. Но делайте свою работу аккуратно!
Выше, где я показал свои чеки, это все, что им нужно. Но делайте свою работу аккуратно!
Кстати, вы можете использовать эту технику «проверки», чтобы проверить свои ответы на любое «решающее» упражнение. Так, например, если вы не уверены в своем ответе на вопрос «сомножить и решить» в следующем тесте, попробуйте подставить свои ответы в исходное уравнение и убедиться, что ваши решения приводят к верным утверждениям.
Это уравнение не в форме «(квадратичное) равно (нулю)», поэтому я пока не могу его решить.Первое, что мне нужно сделать, это переставить все члены с одной стороны и с нулем с другой. Только тогда я могу разложить и решить:
х 2 – 3 = 2 х
х 2 – 2 х – 3 = 0
( х – 3)( х + 1) = 0
х – 3 = 0, х + 1 = 0
х = 3, х = –1
Тогда мое решение:
Решите (
х + 2)( х + 3) = 12.

Студенты очень часто видят уравнение такого типа и говорят:
«Круто! Это уже учтено! Так что я установлю множители равными 12 и решу, чтобы получить x = 10 и x = 9. Это было легко!»
Да, это было легко; это тоже было неправильно. Очень, очень неправильно.
Помимо того факта, что ни (10 + 2)(10 + 3), ни (9 + 2)(9 + 3) не равны 12, мы никогда не должны забывать, что мы должны иметь «(квадратичное) равно (ноль)», прежде чем мы сможем решить факторингом.
Возврат к упражнению:
Каким бы заманчивым это ни казалось, я не могу приравнять каждый из факторов в левой части уравнения к другой части уравнения и решить. Это дало бы мне совершенно неправильный беспорядок.
Вместо этого я сначала должен умножить и упростить левую часть, затем вычесть 12 из левой части и провести рефакторинг. Только тогда я могу решить.
Только тогда я могу решить.
( х + 2)( х + 3) = 12
х 2 + 5 х + 6 = 12
х 2 + 5 х – 6 = 0
( х + 6)( х – 1) = 0
х + 6 = 0, х – 1 = 0
х = –6, х = 1
Тогда мое решение:
Этот двухчленный квадратик легче разложить на множители, чем предыдущие квадратичные числа: я сразу вижу, что могу разложить на множители x из обоих членов, вынеся x впереди.Это дает мне:
Очень распространенная ошибка, которую допускают учащиеся на этом этапе, заключается в том, что они «решают» уравнение для « x + 5 = 0» путем деления на x . Но это неверный шаг. Почему? Потому что мы не можем делить на ноль. Как это вступает в игру здесь?
Но это неверный шаг. Почему? Потому что мы не можем делить на ноль. Как это вступает в игру здесь?
Деление на коэффициент x делает неявное предположение, что x не равно нулю.Для такого предположения нет абсолютно никаких оснований! И если мы сделаем это предположение, мы потеряем половину нашего решения этого уравнения.
Возврат к упражнению:
Мне нужно помнить, что фактор может содержать только переменную, не добавляясь к другим терминам; в частности, « x » является вполне допустимым фактором. Мне нужно установить обоих множителей равными нулю, а затем решить два получившихся линейных уравнения:
х ( х + 5) = 0
х = 0, х + 5 = 0
х = 0, х = –5
Тогда мое решение:
В предыдущем примере было два термина, и его было легко разложить на множители. Есть еще один случай двухчленных квадратичных уравнений, который мы можем решить с помощью факторизации. Только немного сложнее:
Есть еще один случай двухчленных квадратичных уравнений, который мы можем решить с помощью факторизации. Только немного сложнее:
Это уравнение находится в форме «(квадратичное) равно (нулю)», так что я готов решить его с помощью факторизации. Но как мне это учесть? Заметив, что это разность квадратов. Я применю формулу разности квадратов, которую выучил наизусть:
х 2 – 4 = 0
( х — 2)( х + 2) = 0
х – 2 = 0, х + 2 = 0
х = 2, х = –2
Тогда мое решение:
Примечание. Приведенное выше решение также можно отформатировать как « x = ± 2».Это произносится как « x равно плюс-минус 2».
Последний приведенный выше пример подводит нас к тому, как решать, извлекая квадратный корень, на следующей странице.
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в решении квадратных уравнений с помощью факторизации. Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите кнопку и выберите «Решить с помощью факторинга», чтобы сравнить свой ответ с ответом Mathway. (Или перейдите на следующую страницу.)
(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.)
URL-адрес: https://www.purplemath.com/modules/solvquad.htm
Выразите многочлен как произведение линейных коэффициентов
Объяснение:
Мы начинаем с попытки найти любые рациональные корни, используя теорему о рациональных корнях, которая утверждает, что возможные рациональные корни являются положительными или отрицательными версиями возможных дробных комбинаций, образованных путем помещения множителя постоянного члена в числитель и множитель старшего коэффициента в знаменателе.
В одном предложении было много слов, так что давайте разберем это. Начнем с нашего многочлена.
Постоянный терм — это терм без переменной (простое число). В нашем случае константа равна 60. Каковы возможные коэффициенты 60?
Старший коэффициент — это число перед наибольшей степенью переменной. Когда термины перечислены в порядке убывания (от наибольшей степени к наименьшей), старший коэффициент всегда является первым числом.В нашем случае старший коэффициент трудно обнаружить. Поскольку перед нет числа, коэффициент по умолчанию равен 1.
Это хорошо, потому что единственный множитель 1 хорошо… 1.
Затем мы создаем все возможные дроби с коэффициентом константы в числителе и коэффициентом старшего коэффициента в знаменателе. На самом деле это не так плохо, как могло бы быть, поскольку наш единственный возможный знаменатель равен 1. Любая дробь со знаменателем, равным 1, является просто числителем.Следовательно, наши возможные «дроби» равны просто
.
Однако мы должны рассмотреть их положительные и отрицательные версии, поэтому наш окончательный список возможных рациональных корней таков:
К сожалению, здесь процесс (по крайней мере, без помощи графического калькулятора) становится менее увлекательным. Используя синтетическое деление, мы должны просто пробовать каждый возможный корень, пока не добьемся успеха. На самом деле не существует последовательного правила, которое говорило бы нам, с чего начать. Обычно лучше всего начинать с меньших целых чисел, потому что синтетическое деление проще.Следовательно, мы могли бы начать с , затем перейти к и т. д.
Чтобы сделать это объяснение как можно короче, я сразу перейду к пункту 2, где мы сначала добьемся успеха.
Следовательно, 2 — это корень. Однако всегда важно проверить, действительно ли корень является двойным корнем (это работает дважды). Поэтому попробуем еще раз.
2 на самом деле работает дважды и, таким образом, является двойным корнем. Поскольку у нас осталось только три термина, мы можем преобразовать синтетическое выражение обратно в алгебраическое.
Поскольку у нас осталось только три термина, мы можем преобразовать синтетическое выражение обратно в алгебраическое.
Затем мы можем разложить на множители.
Запись нашего корня из 2 в виде алгебраического выражения дает . Так как у нас есть двойной корень, нам нужно два из них. Следовательно, наше окончательное факторизованное выражение таково.
Видео Вопрос: Нахождение множества нулей кубической функции
Стенограмма видео
Найдите множество нулей функции 𝑓 от 𝑥 равно 𝑥 в кубе плюс пять 𝑥 в квадрате минус девять 𝑥 минус 45.
Это полиномиальная функция. В частности, это кубическая функция. И мы собираемся найти нули этой функции, пытаясь разложить на множители имеющееся у нас кубическое выражение. Мы можем разделить члены этого кубического выражения на две группы. Одна из них равна 𝑥 в кубе плюс пять 𝑥 в квадрате, а другая — минус девять 𝑥 минус 45. Мы можем заметить, что обе группы имеют множитель 𝑥 плюс пять. 𝑥 в кубе плюс пять 𝑥 в квадрате равно 𝑥 в квадрате, умноженному на 𝑥 плюс пять, а минус девять 𝑥 минус 45 равно минус девяти, умноженному на 𝑥 плюс пять.
𝑥 в кубе плюс пять 𝑥 в квадрате равно 𝑥 в квадрате, умноженному на 𝑥 плюс пять, а минус девять 𝑥 минус 45 равно минус девяти, умноженному на 𝑥 плюс пять.
Теперь, когда у нас есть две вещи с общим множителем, мы можем объединить их, чтобы получить 𝑥 в квадрате минус девять, умноженное на 𝑥 плюс пять. Таким образом, мы несколько умножили 𝑓 из 𝑥; мы записали его как произведение двух факторов. Но мы замечаем, что множитель 𝑥 в квадрате минус девять — это разница в два квадрата, и поэтому его можно разложить на множители. 𝑥 в квадрате минус девять равно 𝑥 плюс три, умноженное на 𝑥 минус три. Итак, 𝑓 из 𝑥 равно 𝑥 плюс три раза 𝑥 минус три раза 𝑥 плюс пять.
Теперь, когда мы полностью разложили 𝑓 из 𝑥, мы можем найти его множество нулей.Мы хотели найти множество значений 𝑥, для которых 𝑓 of 𝑥 равно нулю. Используя факторизованную форму 𝑓 из 𝑥, мы получаем, что 𝑥 плюс три раза 𝑥 минус три раза 𝑥 плюс пять равно нулю. У нас есть произведение трех чисел, равное нулю, и это может произойти только в том случае, если одно из этих чисел равно нулю. Таким образом, либо 𝑥 плюс три равно нулю, либо 𝑥 минус три равно нулю, либо 𝑥 плюс пять равно нулю. Итак, 𝑥 равно минус трем, или 𝑥 равно трем, или 𝑥 равно минус пяти.
Таким образом, либо 𝑥 плюс три равно нулю, либо 𝑥 минус три равно нулю, либо 𝑥 плюс пять равно нулю. Итак, 𝑥 равно минус трем, или 𝑥 равно трем, или 𝑥 равно минус пяти.
В вопросе нас просят указать набор нулей. Итак, нам нужно поместить эти три значения в набор. 𝑥 находится в наборе, который содержит отрицательную пятерку, тройку и отрицательную тройку. Порядок, в котором мы пишем элементы набора, не имеет значения. Если 𝑥 является нулем функции 𝑓 от 𝑥, то это либо отрицательная пятерка, либо тройка, либо отрицательная тройка.
Итак, набор нулей 𝑓 of 𝑥, который, в конце концов, и есть то, что мы ищем, — это набор минус пять, три и минус три.
Учебное пособие по алгебраическому калькулятору
— MathPapa
Это учебное пособие о том, как использовать алгебраический калькулятор , пошаговый калькулятор для алгебры.
Решение уравнений
Сначала перейдите на главную страницу алгебраического калькулятора. В текстовом поле калькулятора вы можете ввести математическую задачу, которую хотите вычислить. (Показатель: «возведён в степень»)
(Показатель: «возведён в степень»)
График
Чтобы построить график уравнения, введите уравнение, начинающееся с «y=» или «x=».2.
Вычисление выражений
Алгебра Калькулятор может вычислять выражения, содержащие переменную x.
Чтобы вычислить выражение, содержащее x, введите выражение, которое вы хотите вычислить, затем знак @ и значение, которое вы хотите подставить вместо x.
Например, команда 2x @ 3 оценивает выражение 2x для x=3, что равно 2*3 или 6.
Алгебра Калькулятор также может вычислять выражения, содержащие переменные x и y.Чтобы вычислить выражение, содержащее x и y, введите выражение, которое вы хотите вычислить, затем знак @ и упорядоченную пару, содержащую ваши значения x и y. Вот пример вычисления выражения xy в точке (3,4): xy@(3,4).
Проверка ответов для решения уравнений
Точно так же, как алгебраический калькулятор можно использовать для вычисления выражений,
Калькулятор алгебры также можно использовать для проверки ответов при решении уравнений, содержащих x.
В качестве примера предположим, что мы решили 2x+3=7 и получили x=2.Если мы хотим снова подставить 2 в исходное уравнение, чтобы проверить нашу работу, мы можем сделать так: 2x+3=7 @ 2. Поскольку ответ правильный, алгебраический калькулятор показывает зеленый знак равенства.
Если вместо этого мы попробуем значение, которое не работает, скажем, x=3 (попробуйте 2x+3=7 @ 3), алгебраический калькулятор вместо этого покажет красный знак «не равно».
Чтобы проверить ответ на систему уравнений, содержащих x и y, введите два уравнения, разделенные точкой с запятой, затем знак @ и упорядоченную пару, содержащую ваши значения x и y.Пример: х+у=7; х+2у=11@(3,4).
Режим планшета
Если вы используете планшет, например iPad, войдите в режим планшета, чтобы отобразить сенсорную клавиатуру.
Статьи по теме
Назад к Алгебра Калькулятор »
Математическая сцена — Уравнения III- Урок 2
| 2008 Расмус Эф и Джанн Сак Птурссон | Уравнения III |
Урок 2 Уравнения кубической и четвертой степени
Как мы можем решить уравнения, такие как кубическое уравнение
показано здесь?
x 3 − x 2 4x + 4 = 0
Существует чрезвычайно сложная формула для решения
кубические уравнения. Некоторые калькуляторы имеют встроенную формулу и поэтому могут
Некоторые калькуляторы имеют встроенную формулу и поэтому могут
использовать для решения кубических уравнений.
Мы собираемся узнать, как эти уравнения могут быть решены с помощью
факторизация. Если уравнение имеет решения, представляющие собой целые числа a,
b и c, то мы можем факторизовать уравнение следующим образом:
x 3 − x 2 4x + 4 = (x
— а)(х — б)(х — с) = 0
Перемножая скобки, мы видим, что константа
термин 4 должен быть числом, которое мы получаем, когда мы умножаем a, b и c вместе.
абв = 4
Все решения a, b и c должны быть в 4 раза больше, поэтому
не так много целых чисел, которые нам нужно рассмотреть.
У нас есть только следующие возможности:
1, 2 и 4
Хорошо изучите каждое из этих чисел, чтобы определить, какие из них
являются решениями уравнения.
f(1) = 1 3 − 1 2 4×1 +
4 = 0 1 – решение
f(−1) = (−1) 3 − (−1) 2
4×(−1) + 4 = 6
f(2) = 2 3 − 2 2 4×2 +
4 = 0 2 – решение
f(−2) = (−2) 3 − (−2) 2
4×(−2) + 4 = 0 −2 является решением
Теперь мы нашли три решения, поэтому нам не нужно
попробуйте 4 и −4 в качестве куба
уравнение имеет не более трех решений.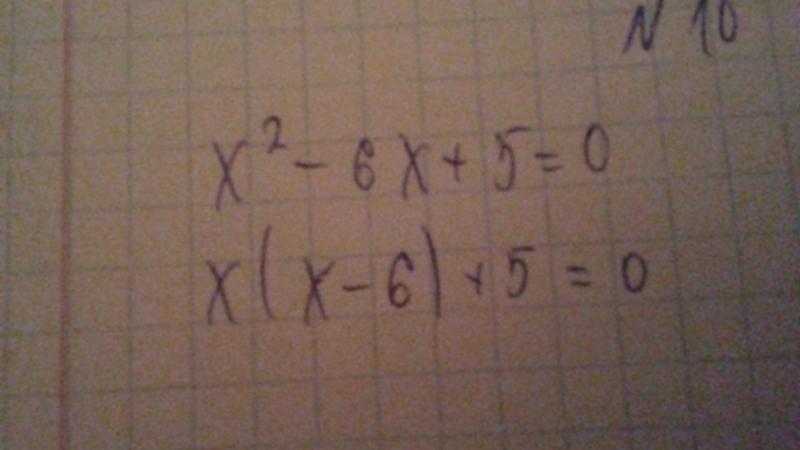
Эти три числа дают нам значения a, b и c и
мы можем факторизовать уравнение.
x 3 − x 2 4x + 4 = (x
− 1)(x − 2)(x + 2) = 0
Этот метод включает в себя нахождение целых чисел, которые являются факторами
(можно разделить на) постоянный член, а затем проверить, являются ли эти
целые числа являются решениями уравнения.
К сожалению, мы не можем считать, что решения уравнения третьей степени
все целые числа.
Однако, если мы можем найти одно целочисленное решение, скажем, это x = a, то по
теореме об остатках, мы знаем, что (x − a) является фактором уравнения. Мы
можно найти другой множитель, квадратичный множитель, путем деления. Затем мы можем решить квадратное уравнение, используя
формула решения квадратного уравнения.
Пример 1
Решите уравнение x 3 − 3x 2 2x + 4 = 0
Складываем числа, делящиеся на 4
в уравнение, чтобы увидеть, является ли какое-либо из них правильным.
f(1) = 1 3 − 3×1 2
2×1 + 4 = 0 1 — решение
f(−1) = (−1) 3 − 3×(−1) 2
2×(−1) + 4 = 2
f(2) = 2 3 − 3×2 2
2×2 + 4 = −4
f(−2) = (−2) 3 − 3×(−2) 2
2×(−2) + 4 = −12
f(4) = 4 3 − 3×4 2
2×4 + 4 = 12
f(−4) = (−4) 3 − 3×(−4) 2
2×(−4) + 4 = −100
Единственным целочисленным решением является x = 1.Когда мы
нашли одно решение, нам действительно не нужно проверять какие-либо другие числа, потому что
теперь мы можем решить уравнение, разделив на (x — 1) и попытавшись решить
квадратичный получается из деления.
Теперь мы можем факторизовать наш
выражение следующим образом:
x 3 − 3x 2 2x + 4 =
(х — 1)(х 2 —
2х — 4) = 0
Теперь нам осталось решить квадратное
уравнение.
x 2 − 2x − 4 = 0
Используем формулу квадратичного уравнения с a = 1, b =
−2 и c = −4.
Теперь мы нашли все три решения задачи.
уравнение x 3 − 3x 2 2x + 4 =
0. Это: eftirfarandi:
х = 1
х = 1 + 5
х = 1 − 5
Пример 2
Мы можем легко использовать тот же метод для решения
уравнение четвертой степени или уравнения еще более высокой степени.Решите уравнение f(x) = x 4 − x 3 − 5x 2 + 3x + 2 = 0,
Сначала находим целые множители
постоянный член, 2. Целые множители 2 равны 1
и 2.
f(1) = 1 4 − 1 3 − 5×1 2 + 3×1 + 2 = 0
1 — решение
f(−1) = (−1) 4 − (−1) 3 − 5×(−1) 2 + 3×(−1) + 2 = −4
f(2) = 2 4 − 2 3 − 5×2 2 + 3×2 + 2 = −4
f(−2) = (−2) 4 − (−2) 3 − 5×(−2) 2 + 3×(−2) + 2 = 0 нашел второй
решение.
Два найденных нами решения 1 и −2 означают, что мы можем делить на x −
1 и х + 2 и остатка не будет. Ну сделайте это в два шага.
Первое деление на x + 2
Теперь разделите полученное
кубический коэффициент на x − 1,
Теперь мы разложили
f(x) = x 4 — x 3 — 5x 2 + 3x + 2 —
f(x) = (x
f(x) 1)(x 2 − 2x − 1) и только
осталось решить квадратное уравнение
х 2 — 2х — 1 = 0.Мы используем
формула с a = 1, b = −2 и c = −1.
Всего мы нашли четыре решения.
Они:
х = 1
х = −2
х = 1 +
х = 1 −
Иногда мы можем решить
уравнение третьей степени, заключая в скобки члены два на два и находя множитель
что у них общего.Давайте посмотрим на пример этого.
Пример 3.
Решите уравнение x 3 − 2x 2 − 4x + 8 = 0
x 3 − 2x 2 − 4x + 8 = 0 (х 3 − 2х 2 ) [х 2 (х — 2) — 4 (х — 2)] = 0 (х — 2) [х 2 — 4] = 0 (х — 2)(х | Здесь скобка (x − 2) является общим делителем и может быть вынесена за общий кронштейн. |
Обратите внимание, что скобка (x
− 2) встречается дважды, когда мы закончили факторизацию. х = 2 это
поэтому двойное решение и у нас есть только два разных.Их:
х = 2 и х = -2 .
Лоуснир: x = 2 og x = −2 .
Все примеры, которые мы рассмотрели до сих пор,
уравнения, где член с наибольшей степенью имеет коэффициент 1,
Как мы
иметь дело с уравнениями, где этот коэффициент является каким-то другим числом?
Общая форма f(x)
= ax 3 + bx 2 + cx + d, где a, b, c и d — целые числа.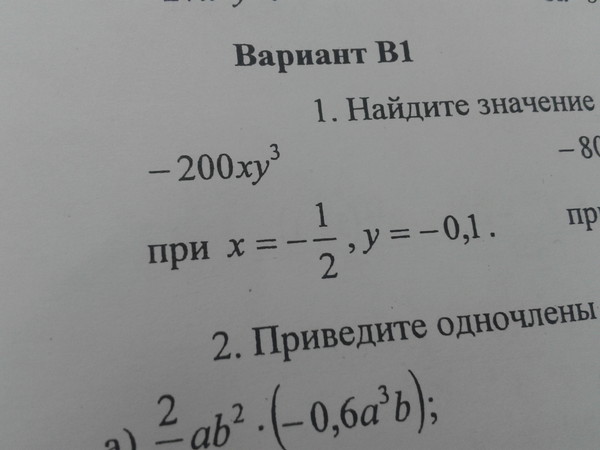
Мы можем искать целочисленные решения в том же
как и раньше, путем проверки факторов постоянного члена d. Если мы найдем
целочисленное решение, то мы можем разделить и найти другие решения, как и раньше.
Если ни один из факторов d не дает нам решения
затем мы ищем решения, которые являются дробями.
Предположим, что есть решение, которое является дробью, и назовем это
решение x = t/n.
Это означает, что x − t/n является фактором
f(x), или, если мы умножим на n, то xn − t будет множителем.
Теперь давайте предположим, что мы разделили f(x) на xn
− t и нашли квадратичный множитель, мы можем назвать его
Ax 2 + Bx + C.
Теперь у нас есть результат, что
ах 3 + бх 2 + сх + д = (хп
− t)(Ax 2 + Bx + C)
сравнивая коэффициенты х 3 на
обе части уравнения мы видим, что a = nA и, следовательно, n должен быть фактором
а.
Аналогично, сравнивая постоянные члены, мы видим, что
d = −tC и, следовательно, t является множителем d.
Заключаем любую дробь, являющуюся решением
кубическое уравнение топор 3 +
bx 2 + cx + d должен иметь вид t/n, где t – множитель числа d, а n –
множитель числа а.
Обобщение для функции степени n:
f(x)
= a n x n + a n-1 x n-1 +
× × × × + а 1 х
+ 0
с коэффициентами а 0 ,
а 1 , а 2 , × × × × × а n−2 ,
n-1 и n .
Если эта функция имеет рациональное решение,
скажем, t/n, тогда t является коэффициентом a 0 , а n является коэффициентом a n .
Пример 4
Решить уравнение f(x) = 2x 3 − 7x 2 + 4x + 3 = 0,
Возможные целые корни f (x) — это
множители 3, они равны 1
и 3.
Дроби, которые могут быть корнями, — это эти четыре числа, разделенные на множители
2.Итак, полный список рациональных чисел, которые нам нужно рассмотреть, это , 1 , 3 / 2 и 3 .
Сразу видно, что нам не нужно
рассмотреть любые отрицательные значения, так как все они будут давать отрицательные значения для f(x), а не
0.
Теперь давайте попробуем другие возможности
f() = 2() 3 − 7() 2 + 4× + 3 = 3
f(1) = 2×1 3 − 7× 2 + 4×1 + 3 = 2
f( 3 / 2 )
= 2 ( 3 / 2 ) 3
— 7 ( 3 / 2 ) 2 + 4 × 3 / 2 + 3 = 0 Итак, мы нашли решение.
x = 3 / 2 является решением, поэтому (x − 3 / 2 ) является множителем.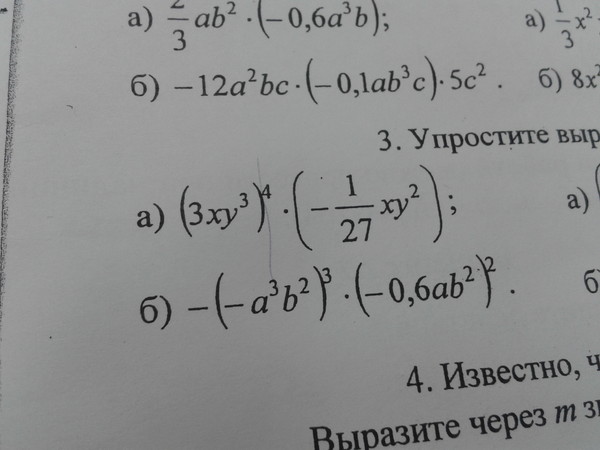
Деление на (x − 3 / 2 ) может быть затруднено. Поэтому мы умножаем на 2 и вместо этого делим на (2x − 3). Если (х
− 3 / 2 ) есть
фактор
, тогда (2x — 3) .
Теперь нам нужно решить уравнение x 2 — 2x — 1 = 0.Мы уже решили это уравнение в примере 2.
Решения были 1 + 2 og 1 — 2,
Итак, мы нашли три решения. Они:
х = 3 / 2 = 1
х = 1 + 2
х = 1 − 2
Попробуйте пройти викторину 2 по уравнениям III.
Не забудьте использовать контрольный список для
следить за своей работой.
.


 3-7x-6= 0 | Wyzant Спросите эксперта
3-7x-6= 0 | Wyzant Спросите эксперта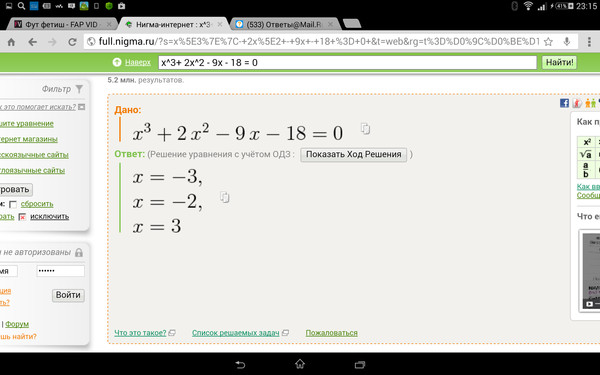
 (x+2) является фактором.
(x+2) является фактором.  Но начнем мы с решения факторингом.
Но начнем мы с решения факторингом.
