Как посчитать объем раствора: Калькулятор по расчету состава раствора для кладочных работ
- Калькулятор расчёта объёма бетона / РБК
- Расчеты при приготовлении водных растворов
- Калькулятор расчета объёма жидкости в цистерне онлайн
- Концентрация раствора — Знаешь как
- процентов (%) решений — PhysiologyWeb
- Исчисление I — Объемы вращающихся тел / Метод колец
- Как рассчитать концентрации при приготовлении разбавлений
- Исчисление I — Дополнительные задачи по объему
Калькулятор расчёта объёма бетона / РБК
 8 (8362) 43-11-12
8 (8362) 43-11-12
- ГЛАВНАЯначало сайта
- ПРОДУКЦИЯкаталог
- ЖЕЛЕЗОБЕТОННЫЕ ИЗДЕЛИЯ
- Ж/б перемычки
- Ж/б кольца
- Блоки фундаментные
- ФБС 9.3.6т (0,88*0,3*0,58)
- ФБС 9.4.6т (0,88*0,4*0,58)
- ФБС 9.5.6т (0,88*0,5*0,58)
- ФБС 9.6.6т (0,88*0,6*0,58)
- ФБС 12.3.6т (1,18*0,3*0,58)
- ФБС 12.4.6т (1,18*0,4*0,58)
- ФБС 12.5.6т (1,18*0,5*0,58)
- ФБС 12.6.6т (1,18*0,6*0,58)
- ФБС 24.3.6т (2,38*0,3*0,58)
- ФБС 24.4.6т (2,38*0,4*0,58)
- ФБС 24.5.6т (2,38*0,5*0,58)
- ФБС 24.6.6т (2,38*0,5*0,58)
- Плиты перекрытия колодцев
- Плиты днища колодцев
- Лестничные ступени ЛС 11
- ТОВАРНЫЙ БЕТОН АКЦИЯ!выберите марку:
- КЕРАМЗИТОБЕТОН
- РАСТВОРЫ АКЦИЯ!выберите марку:
- ПЕСЧАНО-ЦЕМЕНТНАЯ СМЕСЬвыберите марку:
- ИНЕРТНЫЕ МАТЕРИАЛЫ АКЦИЯ!
- СЕТКА АРМАТУРНАЯ АКЦИЯ!
- ПРОСТРАНСТВЕННЫЕ КАРКАСЫ
- ЖЕЛЕЗОБЕТОННЫЕ ИЗДЕЛИЯ
- УСЛУГИнаши услуги
- ПРАЙС-ЛИСТЫцены и доставка
- СПЕЦТЕХНИКАаренда
- ВОСХОДстроительство
- ИНФОРМАЦИЯконтакты и отзывы
- О КОМПАНИИо компании РБК
Расчеты при приготовлении водных растворов
Приблизительные растворы. При приготовлении приблизительных растворов количества веществ, которые должны быть взяты для этого, вычисляют с небольшой точностью. Атомные веса элементов для упрощения расчетов допускается брать округленными иногда до целых единиц. Так, для грубого подсчета атомный вес железа можно принять равным 56 вместо точного —55,847; для серы — 32 вместо точного 32,064 и т. д.
Вещества для приготовления приблизительных растворов взвешивают на технохимических или технических весах.
Принципиально расчеты при приготовлении растворов совершенно одинаковы для всех веществ.
Количество приготовляемого раствора выражают или в единицах массы (г, кг), или в единицах объема (мл, л), причем для каждого из этих случаев вычисление количества растворяемого вещества проводят по-разному.
Пример. Пусть требуется приготовить 1,5 кг 15%-ного раствора хлористого натрия; предварительно вычисляем требуемое количе-ство соли. Расчет проводится согласно пропорции:
т. е. если в 100 г раствора содержится 15 г соли (15%), то сколько ее потребуется для приготовления 1500 г раствора?
Расчет показывает, что нужно отвесить 225 г соли, тогда воды иужио взять 1500 — 225 = 1275 г. ¦
Если же задано получить 1,5 л того же раствора, то в этом случае по справочнику узнают его плотность, умножают последнюю на заданный объем и таким образом находят массу требуемого количества раствора. Так, плотность 15%-нoro раствора хлористого натрия при 15 0C равна 1,184 г/см3. Следовательно, 1500 мл составляет
Следовательно, количество вещества для приготовления 1,5 кг и 1,5 л раствора различно.
Расчет, приведенный выше, применим только для приготовления растворов безводных веществ. Если взята водная соль, например Na2SO4-IOh3O1 то расчет несколько видоизменяется, так как нужно принимать во внимание и кристаллизационную воду.
Пример. Пусть нужно приготовить 2 кг 10%-ного раствора Na2SO4, исходя из Na2SO4 *10h3O.
Молекулярный вес Na2SO4 равен 142,041, a Na2SO4*10h3O 322,195, или округленно 322,20.
Расчет ведут вначале па безводную соль:
Следовательно, нужно взять 200 г безводной соли. Количество десятиводной соли находят из расчета:
Воды в этом, случае нужно взять: 2000 — 453,7 =1546,3 г.
Так как раствор не всегда готовят с пересчетом на безводную соль, то на этикетке, которую обязательно следует наклеивать на сосуд с раствором, нужно указать, из какой соли приготовлен раствор, например 10%-ный раствор Na2SO4 или 25%-ный Na2SO4*10h3O.
Часто случается, что приготовленный ранее раствор нужно разбавить, т. е. уменьшить его концентрацию; растворы разбавляют или по объему, или по массе.
Пример. Нужно разбавить 20%-ный раствор сернокислого аммония так, чтобы получить 2 л 5%-иого раствора. Расчет ведем следующим путем. По справочнику узнаем, что плотность 5%-ного раствора (Nh5)2SO4 равна 1,0287 г/см3. Следовательно, 2 л его должны весить 1,0287*2000 = 2057,4 г. В этом количестве должно находиться сернокислого аммония:
Теперь можно подсчитать, сколько нужно взять 20%-ного рас* твора, чтобы получить 2 л 5%-ного раствора.
Полученную массу раствора можно пересчитать на объем его. Для этого массу раствора делят на его плотность (плотность 20%-ного раствора равна 1.1149 г/см3), т. е.
Учитывая, что при отмеривании могут произойти потери, нужно взять 462 мл и довести их до 2 л, т. е. добавить к ним 2000—462 = = 1538 мл воды.
Если же разбавление проводить по массе, расчет упрощается. Но вообще разбавление проводят из расчета на объем, так как жидкости, особенно в больших количествах, легче отмерить по объему, чем взвесить.
Нужно помнить, что при всякой работе как с растворением, так и с разбавлением никогда не следует выливать сразу всю воду в сосуд. Водой ополаскивают несколько раз ту посуду, в которой проводилось взвешивание или отмеривание нужного вещества, и каждый раз добавляют эту воду в сосуд для раствора.
Когда не требуется особенной точности, при разбавлении растворов или смешивании их для получения растворов другой концентрации можно пользоваться следующим простым и быстрым способом.
Возьмем разобранный уже случай разбавления 20%-ного раствора сернокислого аммония до 5%-ного. Пишем вначале так:
где 20 — концентрация взятого раствора, 0 — вода и 5’—-требуемая концентрация. Теперь из 20 вычитаем 5 и полученное значение пишем в правом нижнем углу, вычитая же нуль из 5, пишем цифру в правом верхнем углу. Тогда схема примет такой вид:
Это значит, что нужно взять 5 объемов 20%-ного раствора и 15 объемов воды. Конечно, такой расчет не отличается точностью.
Если смешивать два раствора одного и того же вещества, то схема сохраняется та же, изменяются только числовые значения. Пусть смешением 35%-ного раствора и 15%-ного нужно приготовить 25%-ный раствор. Тогда схема примет такой вид:
т. е. нужно взять по 10 объемов обоих растворов. Эта схема дает приблизительные результаты и ею можно пользоваться только тогда, когда особой точности не требуется.Для всякого химика очень важно воспитать в себе привычку к точности в вычислениях, когда это необходимо, и пользоваться приближенными цифрами в тех случаях, когда это не повлияет на результаты работы.Когда нужна большая точность при разбавлении растворов, вычисление проводят по формулам.
Разберем несколько важнейших случаев.
Приготовление разбавленного раствора. Пусть с — количество раствора, m%—концентрация раствора, который нужно разбавить до концентрации п%. Получающееся при этом количество разбавленного раствора х вычисляют по формуле:
а объем воды v для разбавления раствора вычисляют по формуле:
Смешивание двух растворов одного и того же вещества различной концентрации для получения раствора заданной концентрации. Пусть смешиванием а частей m%-ного раствора с х частями п%-ного раствора нужно получить /%-ный раствор, тогда:
Точные растворы. При приготовлении точных растворов вычисление количеств нужных веществ проверят уже с достаточной степенью точности. Атомные весы элементов берут по таблице, в которой приведены их точные значения. При сложении (или вычитании) пользуются точным значением слагаемого с наименьшим числом десятичных знаков. Остальные слагаемые округляют, оставляя после запятой одним знаком больше, чем в слагаемом с наименьшим числом знаков. В результате оставляют столько цифр после запятой, сколько их имеется в слагаемом с наименьшим числом десятичных знаков; при этом производят необходимое округление. Все расчеты производят, применяя логарифмы, пятизначные или четырехзначные. Вычисленные количества вещества отвешивают только на аналитических весах.
Взвешивание проводят или на часовом стекле, или в бюксе. Отвешенное вещество высыпают в чисто вымытую мерную колбу через чистую сухую воронку небольшими порциями. Затем из промывалки несколько раз небольшими порциями воды обмывают над воронкой бнже или часовое стекло, в котором проводилось взвешивание. Воронку также несколько раз обмывают из промывалки дистиллированной водой.
Для пересыпания твердых кристаллов или порошков в мерную колбу очень удобно пользоваться воронкой, изображенной на рис. 349. Такие воронки изготовляют емкостью 3, 6, и 10 см3. Взвешивать навеску можно непосредственно в этих воронках (негигроскопические материалы), предварительно определив их массу. Навеска из воронки очень легко переводится в мерную колбу. Когда навеска пересыпается, воронку, не вынимая из горла колбы, хорошо обмывают дистиллированной водой из промывалки.
Как правило, при приготовлении точных растворов и переведении растворяемого вещества в мерную колбу растворитель (например, вода) должен занимать не более половины емкости колбы. Закрыв пробкой мерную колбу, встряхивают ее до полного растворения твердого вещества. После этого полученный раствор дополняют водой до метки и тщательно перемешивают.
Молярные растворы. Для приготовления 1 л 1 M раствора какого-либо вещества отвешивают на аналитических весах 1 моль его и растворяют, как указано выше.
Пример. Для приготовления 1 л 1 M раствора азотнокислого серебра находят в таблице или подсчитывают молекулярную массу AgNO3, она равна 169,875. Соль отвешивают и растворяют в воде.
Если нужно приготовить более разбавленный раствор (0,1 или 0,01 M), отвешивают соответственно 0,1 или 0,01 моль соли.
Если же нужно приготовить меньше 1 л раствора, то растворяют соответственно меньшее количество соли в соответствущем объеме воды.
Нормальные растворы готовят аналогично, только отвешивая не 1 моль, а 1 грамм-эквивалент твердого вещества.
Если нужно приготовить полунормальный или децинормальный раствор, берут соответственно 0,5 или 0,1 грамм-эквивалента. Когда готовят не 1 л раствора, а меньше, например 100 или 250 мл, то берут1/10 или 1/4 того количества вещества, которое требуется для приготовления I л, и растворяют в соответствующем объеме воды.
Рис 349. Воронки для пересыпания навески а колбу.
После приготовления раствора его нужно обязательно проверить титрованием соответствующим раствором другого вещества с известной нормальностью. Приготовленный раствор может не отвечать точно той нормальности, которая задана. В таких случаях иногда вводят поправку.
В производственных лабораториях иногда готовят точные растворы «по определяемому веществу». Применение таких растворов облегчает расчеты при анализах, так как достаточно умножить объем раствора, пошедший на титрование, на титр раствора, чтобы получить содержание искомого вещества (в г) во взятом для анализа количестве какого-либо раствора.
Расчет при приготовлении титрованного раствора по определяемому веществу ведут также по грамм-эквиваленту растворяемого вещества, пользуясь формулой:
Пример. Пусть нужно приготовить 3 л раствора марганцовокислого калия с титром по железу 0,0050 г/мл. Грамм-эквивалент KMnO4 равен 31,61., а грамм-эквивалент Fe 55,847.
Вычисляем по приведенной выше формуле:
Стандартные растворы. Стандартными называют растворы с разными, точно определенными концентрациями, применяемые в колориметрии, например растворы, содержащие в 1 мл 0,1, 0,01, 0,001 мг и т. д. растворенного вещества.
Кроме колориметрического анализа, такие растворы бывают нужны при определении рН, при нефелометрических определениях и пр. Иногда стандартные растворы» хранят в запаянных ампулах, однако чаще приходится готовить их непосредственно перед применением. Стандартные растворы готовят в объеме не больше 1 л, а ча ще — меньше. Только при большом расходе стандартного раствори можно готовить несколько литров его и то при условии, что стандартный раствор не будет храниться длительный срок.
Количество вещества (в г), необходимое для получения таких растворов, вычисляют по формуле:
Пример. Нужно приготовить стандартные растворы CuSO4 • 5h3O для колориметрического определения меди, причем в 1 мл первого раствора должно содержаться 1 мг меди, второго — 0,1 мг, третьего —0,01 мг, четвертого — 0,001 мг. Вначале готовят достаточное количество первого раствора, например 100 мл.
В данном случае Mi = 249,68; АСu = 63,54; следовательно, для приготовления 100 мл раствора, 1 мл которого содержал бы 1 мг меди (Т = 0,001 г/мл), нужно взять
Навеску соли переносят в мерную колбу емкостью 100 мл и добавляют воду до метки. Другие растворы готовят соответствующим разбавлением приготовленного.
Эмпирические растворы. Концентрацию этих растворов чаще всего выражают в г/л или г/мл. Для приготовления эмпирических растворов применяют очищенные перекристаллизацией вещества или реактивы квалификации ч. д. а. или х. ч.
Пример. Нужно приготовить 0,5 л раствора CuSO4, содержашего Cu 10 мг/мл. Для приготовления раствора применяют CuSO4 • 5h3O.
Чтобы подсчитать, сколько следует взять этой солн для приготовления раствора заданного объема, подсчитывают, сколько Cu должно содержаться в нем. Для этого объем умножают на заданную концентрацию, т. е.
500*10 = 5000 мг, или 5,0000 г
После этого, зная молекулярный вес соли, подсчитывают нужное количество ее:
На аналитических весах отвешивают в бюксе точно 19,648 г чистой соли, переводят ее в мерную колбу емкостью 0,5 л. Растворение проводят, как указано выше.
К оглавлению
см. также
- Основные понятия о растворах
- Классификация растворов
- Концентрация растворов
- Техника приготовления растворов
- Расчеты при приготовлении водных растворов
- Растворы солей
- Растворы щелочей
- Растворы кислот
- Фиксаналы
- Некоторые замечания о титровании и точных растворах
- Расчеты при титровании с помощью весовых бюреток
- Рациональные величины
- Растворение жидкостей
- Растворение газов
- Индикаторы
- Автоматическое титрование
- Неводные растворы
- Растворение в органических растворителях
- Обесцвечивание растворов
Калькулятор расчета объёма жидкости в цистерне онлайн
Инструкция для калькулятора количества и объема жидкости в цистерне
Размеры вводите в миллиметрах:

D – диаметр емкости можно замерить рулеткой. Необходимо помнить что диаметр – это отрезок наибольшей длины, соединяющий две точки на окружности и проходящий через ее центр.
H – уровень жидкости замеряют, используя метршток, но если такого инструмента нет под рукой, воспользуйтесь обычным стержнем из проволоки или деревянной планкой подходящей длины. Соблюдая меры безопасности, опустите строго вертикально стержень в цистерну до дна, отметьте на нем уровень, достаньте и измерьте рулеткой. Также определить H можно, измерив, расстояние от верха цистерны до поверхности жидкости и отняв этот показатель от значения диаметра.
L – длина емкости.
Если необходим чертеж в бумажном виде, целесообразно отметить пункт «Черно-белый чертеж». Вы получите контрастное изображение и сможете его распечатать, не расходуя зря цветную краску или тонер.
Нажмите «Рассчитать» и получите следующие данные:
Объём емкости – этот параметр характеризует полный объём цистерны, т.е. какое максимальное количество жидкости в кубических метрах или литрах может в нее поместиться.
Количество жидкости – сколько вещества находится в цистерне на данный момент.
Свободный объём позволяет оценить, сколько жидкости еще можно залить в емкость.
В результате, Вы получаете расчет не только объема цистерны, но и объема жидкости в неполной цистерне.
Изделия из металла следует периодически красить, тогда срок их службы значительно возрастет. Зная площадь передней поверхности, площадь боковой поверхности и общую площадь емкости легко оценить необходимое количество лакокрасочных материалов для обработки всей емкости или ее отдельных частей.
Концентрация раствора — Знаешь как
Содержание статьи

Весовая процентная концентрация показывает, какой процент от общего веса раствора составляет растворенное вещество.
■ 18. Сколько нитрата калия нужно взять для приготовления 300 г 2% раствора соли?
19? Сколько воды и сахара требуется для приготовления 250 г 10% раствора?
20. Сколько хлорида бария потребуется для приготовления 50 г 0,5% раствора? (См. Ответ)
В лабораторной практике часто приходится иметь дело с кристаллогидратами — солями, содержащими кристаллизационную воду, например CuSО4 ·5H2O, FeSО4 · 7H2О и т. д. В этом случае следует уметь учитывать кристаллизационную воду.
Пример 1. Сколько соли нужно для приготовления 500 г 3% ее раствора? | |
Дано: 500 г. 3% раствора соли | Решение: Если сказано, что имеется 3% раствор, это значит, что в любом количестве этого раствора содержится 3% соли. Чтобы рассчитать, сколько нужно соли для приготовления 500 г такого раствора, следует найти 3% от 500 г: (500 · 3) : 100 = 15г Следовательно, соли нужно 15 г, а воды 500— 15 = 485 г. |
Пример 2. Сколько кристаллогидрата медного купороса нужно взвесить, чтобы получить 200 г 5% раствора сульфата меди? Сколько воды нужно для этого взять? | |
Дано: 200 г 5% CuSO4 | Решение: Сначала требуется определить, сколько сульфата меди CuSО4 нужно для приготовления заданного количества раствора: (200 · 5) :100 = 10 г. CuSO4. Далее делаем пересчет на кристаллогидрат: грамм-молекула CuSO4 весит 160 г, а грамм-молекула CuSO4 · 5H2О весит 250 г. Следовательно, мы можем составить пропорцию: 160 г CuSO4— в 250 г CuSO4 · 5H2О 10» CuSО4 — » х » CuSO4· 5Н2О X=(250 · 10) : 160 = 15,625 г. Воды для приготовления раствора требуется 200— 16,6 15= 184,375 г. |
■ 21. Сколько кристаллогидрата Na2SO4 · 10H2O понадобится для приготовления 2 кг 34 раствора Na2SО4?
22. Сколько кристаллогидрата железного купороса FeSO4·7h3O потребуется для приготовления 30 кг 0,5% раствора FeSO4?
23. Сколько кристаллогидрата CaCl2 · 6H2O потребуется для приготовления 500 г 10% раствора СаСl2?
24. Сколько кристаллогидрата ZnSO4· 7H2O потребуется для приготовления 400 г 0,1 % раствора ZuSО4? (См. Ответ)
Иногда приходится приготовлять растворы определенной процентной концентрации, пользуясь для этого другими, более концентрированными растворами. Особенно часто с этим приходится сталкиваться в лаборатории при получении растворов кислот разной концентрации.
Пример 3. Сколько требуется 80% серной кислоты для приготовления 200 г 10% раствора этой кислоты?. Обозначим массу первого раствора m1, массу второго — m2, концентрацию первого раствора С1, концентрацию второго раствора C2. | |
Дано: m1 = 200г C1 = 10% C2 = 80%
| Прежде всего нужно выяснить, сколько чистой безводной серной кислоты потребуется для приготовления 200 г. 10% раствора: (200 · 10) : 100 = 20 г. Определяем, в каком количестве 80% серной кислоты содержится 20 г чистой кислоты, рассуждая так: в 100 г 80% H2SО4 — 80 г чистой H2SО4 » х » 80% H2SО4 —20 » »H2SО4. Отсюда х = (100 · 20) : 80 = 25 г 80% раствора. Следовательно, для нашей цели нужно 25 г 80% раствора H2SО4 и 200—25 = 175 г воды. |
■ 25. Сколько потребуется 80% фосфорной кислоты для приготовления 2 кг 5% раствора?
26. Сколько потребуется 20% щелочи для приготовления 5 кг. 1 % раствора?
27. Сколько потребуется 15% азотной кислоты для приготовления 700 г 5% раствора?
28. Сколько потребуется 40% серной кислоты для приготовления 4 кг 2% раствора?
29. Сколько потребуется 10% соляной кислоты для приготовления 500 г 0,5% раствора? (См. Ответ)
Однако произвести правильный расчет — это для лаборанта еще не все. Нужно уметь не только рассчитать, но и приготовить раствор кислоты. Но кислоты нельзя взвешивать на весах, их можно только отмерять при помощи мерной посуды. Мерная же посуда предназначена для измерений объема, а не веса. Поэтому нужно суметь вычислить объем найденного количества раствора. Этого нельзя сделать, не зная удельного веса (плотности) раствора.
Обратимся снова к примеру 3, приведен ному на стр 67. Из таблицы (приложение III, п. 3, стр. 394) видно, что 80% серная кислота имеет плотность d=1,7, а масса раствора Р =25 г. Следовательно, по формуле
V = P : d находим: V = 25 : 1,7 = 14,7 мл.
Плотность воды практически считаем равной единице. Следовательно, 175 г воды займут объем 175 мл. Таким образом, чтобы приготовить 200 г 10% раствора из 80% серной кислоты, следует взять 175 мл воды и налить в нее 14,7 мл 80% серной кислоты. Смешивание можно производить в любой химической посуде.
■ 30. Сколько миллилитров 50% серной кислоты следует взять для приготовления 2 кг 10% раствора этой кислоты?
31. Сколько миллилитров 40% серной кислоты следует взять для приготовления 5 л 4% серной кислоты?
32. Сколько миллилитров 34% едкого кали потребуется для приготовления 10 л 10% раствора?
33. Сколько миллилитров 30% соляной кислоты потребуется для приготовления 500 мл 2% соляной кислоты? (См. Ответ)
Примеры расчетов, которые мы разбирали до сих пор, были посвящены определению веса или объема раствора, а также количества вещества, содержащегося в нем. Однако бывают случаи, когда нужно определить концентрацию раствора. Рассмотрим простейший случай.
Пример 4, Рассчитайте, какова процентная концентрация раствора, если смешано 45 г воды и 5 г соли. | |
Дано: mh3O = 45г mсоли = 5г
| Решение: Сначала определяем общее количество раствора: 45 г + 5 г = 50 г. Затем определяем процентную концентрацию: (5 : 50) · 100 = 10% Следовательно раствор 10%. |
■ 34 Смешано 25 г соли и 35 г воды. Какова процентная концентрация раствора?
35. Смешано 5 г кислоты и 75 г воды. Какова процентная концентрация раствора? (См. Ответ)
Довольно часто приходится разбавлять, упаривать и смешивать растворы, после чего определять их концентрацию.
Пример 5. К 250 г 10% раствора добавили 150 г воды Какой стала концентрация раствора? | |
Дано: m1 = 250г C1 = 10% mh3O = 150г
| Решение: Сначала рассчитываем содержи ние вещества в 250 г раствора: (250 · 10) : 100 = 25 г. Определяем общее количество получившегося раствора: 250 + 150 = 400 г. Поскольку мы к раствору приливали только воду, а растворенное вещество не добавляли, то его количество осталось, очевидно, таким же. Следовательно, в 400 г полученного раствора содержится 25 г вещества, а его процентная концентрация (25 : 400) · 100 = 6,25% |
■ 36. К 2 кг 20% раствора прилили 500 г воды. Какой стала концентрация раствора?
37. К 5 а 36% соляной кислоты прилили 1 л воды. Какой стала концентрация раствора?
38. Смешали 40 кг 2% и 10 кг 3% растворов одного и того же вещества. Какой стала концентрация полученного раствора?
39. Смешали 4 л 28% серной кислоты и 500 мл 60% серной кислоты. Какова концентрация полученного раствора?
40. 3 кг 20% раствора едкого натра упарили до 2 кг. Какова концентрация полученного раствора?
41. Сколько воды нужно прибавить к 500 мл 30% раствора (плотность 1,224 г/см3), чтобы получить 5% раствор? (См. Ответ)
Для определения, в каком соотношении следует смешать растворы разных концентраций, чтобы получить раствор искомой концентрации, можно применять так называемое «правило смешивания», или «диагональную
схему»
Пример 6. В каком весовом соотношении следует смешать 40% и 15% растворы, чтобы получить 35% раствор? |
Решение. Для решения составляют диагональную схему: 40→20 \ / 35 / \ 15→5 В центре пишут искомую концентрацию. У левого конца каждой диагонали пишут данные концентрации. Затем по диагонали производят вычитание: 35—15 = 20 40 — 35 = 5 (вычитают всегда из большей величины меньшую). Результат вычитания проставляют у правого конца соответствующей диагонали. Получилось, что смешать требуется 5 в. ч. 15% и 20 в. ч. 40% раствора, т. е. в соотношении 1:4. Если в смешивании участвует вода, ее концентрация берется равной 0%. |
■ 42. Рассчитайте по диагональной схеме, в каком соотношении следует смешать растворы:
а) 20% и 3% для получения 10%;
б) 70% и 17% для получения 25%;
в) 25% и воду для получения 6% (См. Ответ)
Объемная концентрация растворов. Молярная концентрация
При определении объемной концентрации растворов расчеты производят применительно к 1 л раствора. Молярная концентрация, например, показывает сколько грамм-молекул (молей) растворенного вещества содержится в 1 л раствора.
Если вы не помните, что такое грамм-молекула, обратитесь к приложению на стр. 374.
Например, если в 1л раствора содержится 1 моль вещества, то такой раствор называется одномолярным (1 М), если 2 моля, то двумолярным(2 М), если 0,1 моля, тo раствор децимолярный (0,1 М), если 0,01 моля, то раствор сантимолярный (0,01 М) и т. д. Для приготовления растворов молярной концентрации необходимо знать формулу вещества.
Пример 7. Сколько нужно взять едкого натра, чтобы приготовить 200 мл 0,1 М раствора едкого натра NaOH. | |
Дано: V = 200 мл С = 0,1 М
| Решение: Прежде; всего вычислим вес грамм-молекулы едкого натра NaOH. 23 + 16 + 1 = 40 г. Так как раствор 0,1 М, то в 1 л раствора содержится 0,1 грамм-молекулы NaOH, т. е. 4 г, а в 200 мл или в 0,2 л, раствора будет содержаться неизвестное количество NaOH. Составляем пропорцию: в 1 л 0,1 М раствора — 4 г NaOH » 0.2 » » — х » NaOH Отсюда 1 : 0,2 = 4 : x x = (4 · 0,2) : 1 = 0,8 г. т. е. для приготовления 200 мл 0,1 М раствора нужно 0,8 г NaOH. |
Молярная концентрация очень удобна тем, что в равных объемах растворов с одинаковой молярностью содержится одинаковое количество молекул, так как в грамм-молекуле любого вещества содержится одно и то же число молекул.
Готовят раствор молярной концентрации в мерных колбах определенного объема. На шейке такой колбы имеется отметка, точно ограничивающая нужный объем, а надпись на колбе указывает, на какой объем рассчитана данная мерная колба.
■ 43. Рассчитайте, какое количество вещества требуется для приготовления следующих растворов:
а) 5 л 0,1 М раствора серной кислоты;
б) 20 мл 2 М раствора соляной кислоты;
в) 500 мл 0,25 М раствора сульфата алюминия;
г) 250 мл 0,5 М раствора хлорида кальция. (См. Ответ)
Растворы кислот молярной концентрации нередко приходится готовить из процентных растворов.
Пример 8. Сколько требуется 98 % серной кислоты для приготовления 5 л 0,1 М раствора. | |
Дано: V1= 5 л С1= 0,1 М С2 = 98%
| Решение: Определяем содержание чистой серной кислоты в 5 л 0,1 М раствора. 1 моль H2SО4 = 98 г; 0,1 моля H2SО4 = 9,8 г. Для приготовления 5 л 0,1 М раствора H2SО4 необходимо 9,8 · 5 = 49 г чистой H2SО4. Далее найдем, сколько 98% раствора серной кислоты потребуется для приготовления 5 л 0,1 М раствора. Составим пропорцию: в 100 г раствора содержится 98 г h3SО4 » х » » » 49 » H2SO4. Отсюда х = (49 · 100) : 98 = 50 г. |
■ 44. Сколько потребуется 50% азотной кислоты для приготовления 500 мл 0,5 М раствора.
45. Какой объем 98% серной кислоты необходим для приготовления 10 л 3 М раствора?
46. Вычислите молярность следующих растворов:
а) 20% серной кислоты;
б) 4% едкого натра;
в) 10% азотной кислоты;
г) 50% едкого кали. (См. Ответ)
Нормальная концентрация растворов
Нормальная концентрация растворов выражается количеством грамм-эквивалентов растворенного вещества в 1 л раствора. Для того чтобы произвести расчет для Приготовления раствора нормальной концентрации, нужно знать, что такое эквивалент. Слово «эквивалентный» означает «равноценный».
Эквивалентом называется весовое количество элемента, которое может соединяться с 1 весовой частью водорода или замещать ее в соединениях.
Если в молекуле воды Н2О содержится два атома водорода, весящих в сумме 2 у. е., и один атом кислорода, весящий 16 у. е., то на 1 у. е. водорода приходится 8 у. е. кислорода, что и будет эквивалентом кислорода. Если мы возьмем какой-нибудь окисел, например закись железа FeO, то в нем водорода нет, но зато есть кислород, а мы нашли из предыдущего расчета, что 8 у. е. кислорода эквивалентны 1 у. е. водорода. Следовательно, достаточно найти количество железа, способное соединиться с 8 у. е. кислорода, и это также будет его эквивалентом. Атомный вес железа 56. В окисле 56 у. е. Fe приходится на 16 у. е. кислорода, а на 8 у. е. кислорода железа придется вдвое меньше.
Можно найти эквивалент и для сложных веществ, например для серной кислоты H2SО4. В серной кислоте на 1 у. е. водорода приходится половина молекулы кислоты (включая, конечно, и водород), так как кислота двухосновная, т. е. эквивалент серной кислоты равен ее молекулярному весу (98 у. е.), деленному на 2, т. е. 49 у. е.
Эквивалент для основания можно найти, разделив его молекулярный вес на валентность металла Например, эквивалент NaOH равен молекулярному весу (40 у. е.), деленному на 1, т. е. на валентность натрия. Эквивалент NaOH равен 40 у. е. Эквивалент гидроокиси кальция Са(ОН)2 равен молекулярному весу (74 у. е.), деленному на валентность кальция, а именно на 2, т. е. 37 у, е.
Для того чтобы найти эквивалент для какой-нибудь соли, нужно молекулярный вес ее разделить на валентность металла и количество его атомов. Так, молекулярный вес сульфата алюминия Al2(SO4)3 равен 342 у. е. Эквивалент его равен: 342 : (3 · 2) = 57 у.е. где 3 — валентность алюминия, а 2 — количество атомов алюминия.
■ 47. Рассчитайте эквиваленты следующих соединений; а) фосфорной кислоты; б) гидроокиси бария; в) сульфата натрия;г) нитрата алюминия. (См. Ответ)
Грамм-эквивалентом называется количество граммов вещества, численно равное эквиваленту.
Если в 1 л раствора содержится 1 грамм-эквивалент (г-экв) растворенного вещества, то раствор является одно-нормальным (1 н.), если 0,1 грамм-эквивалента, то деци-нормальным (0,1 н.), если 0,01 грамм-эквивалента, то сантинормальным (0,01 н.) и т. д. Для расчета нормальной концентрации растворов также необходимо знать формулу вещества.
Пример 9. Приготовить 300 мл 0,1 н. раствора серной кислоты H2SО4. | |
Дано: V = 300 мл С = 0,1 н.
| Решение: Молекулярный вес H2SО4 равен 98 у. е., эквивалент H2SО4 равен 98 : 2 = 49 у. е., грамм-эквивалент равен 49 г. Так как раствор 0,1 н., то в 1 л его содержится 0,1 г-экв т. е. 4,9 г, нужно же приготовить 300 мл или 0,3 л этого раствора. Поэтому составим пропорцию: 1 : 0,3 = 4,9 : x x = (4,9 · 0,3) : 5 = 1,47 г. т. е. на приготовление 300 мл 0,1 н. раствора серной кислоты пойдет 1,47 г H2SО4. |
Растворы нормальной концентрации, как и молярные, готовят в мерных колбах.
■ 48. Сколько серной кислоты необходимо для приготовления 2 л 0,1 н. раствора?
49. Сколько нужно взять нитрата алюминия, чтобы приготовить 200 мл 0,5 н. раствора? (См. Ответ)
Нередко приходится готовить растворы нормальной концентрации из концентрированных растворов процентной концентрации. Это делается так же, как и при приготовлении растворов молярной концентрации, но рассчитывается не грамм-молекулярный, а грамм-эквивалентный вес .
Сколько нужно взять 60% азотной кислот, чтобы приготовить 200 мл 3 н. раствора? 61. Какой объем 20% серной кислоты необходим для приготовления 20 л 0,1 н. раствора?
Нормальная концентрация очень удобна, так как если растворы имеют одинаковую нормальность, то в равных объемах этих растворов содержатся эквивалентные количества растворенных веществ. Поэтому вещества, содержащиеся в равных объемах таких растворов, реагируют нацело (если, разумеется, вообще могут между собой реагировать). Например, если взять 1,5 л 0,1 н. раствора едкого натра и 0,1 н. раствор соляной кислоты, то для реакции с едким натром потребуется также 1,5 л раствора соляной кислоты.
Чем выше концентрация раствора, тем меньший его объем требуется для реакции, т. е. между объемами растворов реагирующих веществ и их концентрациями существует обратная зависимость, которую можно выразить формулой:

где V — объем, а С — концентрация раствора.
Исходя из этой формулы, можно определить любую из четырех величин, если известны три остальные.
Пример 10. Какова нормальность соляной кислоты, если на нейтрализацию 20 мл ее пошло 30 мл 0,1 и. едкого натра. | |
Дано: V1 = 20 мл V2 = 30 мл С2 = 0,1 н.
| Решение: Подставляя данные задачи в фор мулу, получаем V1 : V2 = C2 : C1 20 : 30 = 0,1 : C1 ; C1 = (0,1 · 30) : 20 = 0,15 н. Следовательно, концентрация соляной кислоты 0,15 н. |
■ 52. На нейтрализацию 10 мл 0,2 н. раствора кислоты пошло 8 мл раствора едкого кали. Какова нормальность раствора едкого кали?
53. Какой объем 0,1 н. раствора едкого натра будет затрачен на реакцию с 25 мл 0,5 н. раствора хлорида железа (III)?
54. Сколько граммов серной кислоты содержится в 300 мл раствора, если на нейтрализацию 5 мл его израсходовано 8 мл 1 н. раствора едкого натра? (См. Ответ)
Подобные расчеты широко применяются в количественном анализе.
Нередко лаборанту нужно знать процентное содержание вещества в растворе той или иной объемной концентрации. В этом случае необходимо научиться производить перерасчет раствора объемной концентрации на весовую и наоборот.
Пример 11. Рассчитать нормальность 10% раствора едкого натра. Плотность раствора 1,115 г/см3. | |
Дано: CNaOH = 10% dNaOH = 1,115
| Решение: Грамм-эквивалент NaOH = 40 : 1 = 40 г. В 100 г раствора содержится 10 г NaOH, что равно = 0,25 г·экв. Объем 100 раствора равен 100 : 1,115 мл, следовательно в 100 : 1,115 мл — 0,25 г · экв NaOH » 1000 » -x » NaOH Отсюда х = (0,25 · 1000 · 1,115) : 100 = 2,7875 н. |
■ 55. Рассчитайте нормальность следующих растворов:
а) 28% раствора едкого кали;
б) 8% раствора едкого натра;
в) 18% раствора соляной кислоты.
56. Смешано 500 мл 20%, 20 мл 0,2 н. и 300 мл 0,5 М растворов серной кислоты. Рассчитайте нормальность и молярность образовавшегося раствора.
57. Какова молярность 40% раствора едкого натра?
58. Какова нормальность 6% раствора едкого кали?
59. Какова нормальность соляной кислоты, если на нейтрализацию 20 мл ее израсходовано 40 мл 0,2 н. раствора гидроокиси кальция?
60. В каких соотношениях надо смешать 20% и 5% растворы одного и того же вещества, чтобы получился 12% раствор?
61. Какой объем 80% раствора серной Кислоты нужно взять, чтобы приготовить 2 л 2н. раствора этой кислоты? (См. Ответ)
Статья на тему Концентрация раствора
Калькулятор
процентов (%) решений — PhysiologyWeb
Расчет процентов (%) решений

Предназначенный для использования как в учебной, так и в исследовательской лаборатории, этот калькулятор (см. Ниже) может использоваться для выполнения ряда различных расчетов для приготовления процентов (%) растворов , начиная с твердого или жидкого материала. Очень часто концентрацию растворов выражают в процентах.Процент означает на 100 частей, где для растворов часть означает меру массы (мкг, мг, г, кг и т. Д.) Или объема (мкл, мл, л и т. Д.). В процентах растворов количество (вес или объем) растворенного вещества выражается в процентах от общего веса или объема раствора. Процентные растворы могут иметь форму % по весу / объему (% по весу / объему или% по весу / объему), % по весу / весу (% по весу или% по весу) или % по объему / объему (об. / об.% или об. / об.%). В каждом случае процентная концентрация рассчитывается как доля веса или объема растворенного вещества, относящаяся к общей массе или объему раствора.
Поскольку процентные решения могут быть выражены тремя различными способами, совершенно необходимо явно указать тип процентного решения. Если эта информация не предоставлена, конечному пользователю остается «угадать», было ли использовано вес / объем%, вес / вес% или объем / объем%. Каждое процентное решение подходит для ряда различных приложений. Например, коммерческие водные реагенты, такие как концентрированные кислоты и основания, обычно выражаются в виде растворов в процентах по массе. Например, коммерчески доступная концентрированная соляная кислота (HCl) составляет 37% по массе (% мас. / Мас.).С другой стороны, многие разбавленные растворы, используемые для биологических исследований, выражаются в процентах по массе / объему (например, 1% додецилсульфат натрия, SDS). Объем / объем% растворенных веществ также являются обычными и используются, когда используются чистые растворенные вещества в жидкой форме. Например, 70% -ный (об. / Об.) Раствор этанола может быть приготовлен растворением 70 мл 100% (то есть 200-процентного) этанола в общем объеме раствора 100 мл.
Другие факторы также могут быть важны при выборе типа процентного раствора для приготовления.Например, если рассматриваемый процентный раствор должен использоваться при сильно различающихся температурах, то лучше приготовить раствор в виде раствора в процентах по весу, поскольку его концентрация не будет зависеть от изменений температуры окружающей среды.
Сделаем важное замечание. Здесь мы использовали «вес» вместо «масса» просто для того, чтобы соответствовать традициям и популярному использованию. Таким образом, растворов мас. / Об.% Следует правильно обозначать как мас. / Об.% .Аналогично, растворы масс. / Масс.% следует обозначать как масс / масс.% или просто масс.% .
Процентное решение уравнений
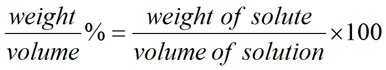 | (уравнение 1) |
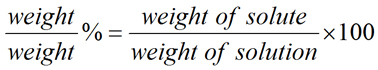 | (уравнение 2) |
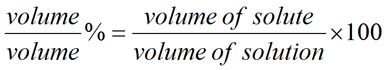 | (Ур.3) |
Как отмечалось выше, вес относится к массе (т. Е. Измеряется на весах). Изучая уравнение для каждого из приведенных выше процентов растворов, очень важно отметить, что во всех случаях знаменатель относится к массе или объему раствора , а не только к массе или объему растворителя. Таким образом, масса раствора — это объединенная масса растворенного вещества и растворителя, а объем раствора — это объединенный объем растворенного вещества и растворителя.
Последнее замечание необходимо при рассмотрении решений объем / объем%.Когда разные объемы одного и того же раствора складываются вместе, конечный объем всегда будет точной суммой добавленных отдельных порций. Например, добавление 50 мл воды к 50 мл воды приведет к общему объему 100 мл, а добавление 75 мл 100% этанола к 75 мл 100% этанола приведет к общему объему 150 мл. Однако при смешивании смешиваемых жидкостей (таких как вода и этанол) конечный объем раствора не точно равен сумме отдельных объемов. Например, добавление 50 мл этанола к 50 мл воды приведет к получению общего объема менее 100 мл.На самом деле это ближе к 96 мл. Следовательно, при приготовлении растворов объем / объемный процент всегда лучше растворить растворенное вещество в растворителе, а затем добавить дополнительный растворитель, чтобы довести общий объем раствора до желаемого конечного значения.
Калькулятор процентного решения
Каждая ячейка калькулятора, показанная ниже, соответствует члену в приведенной выше формуле. Введите соответствующие значения во все ячейки, кроме той, которую вы хотите вычислить. Следовательно, по крайней мере две ячейки должны иметь значения, и не более одной ячейки может быть пустым .Значение пустой ячейки будет рассчитано на основе других введенных значений. После выполнения вычисления вычисленная ячейка будет выделена, и последующие вычисления будут вычислять значение выделенной ячейки (без требования иметь пустую ячейку). Однако пустая ячейка имеет приоритет над выделенной ячейкой.
Комментарии и / или инструкции по приготовлению
Размещено: 5 октября 2013 г., суббота
Последнее обновление: 23 декабря 2017 г.
.
Исчисление I — Объемы вращающихся тел / Метод колец
Онлайн-заметки Павла
Заметки
Быстрая навигация
Скачать
- Перейти к
- Заметки
Проблемы с практикой
Проблемы с назначением
- Показать / Скрыть
- Показать все решения / шаги / и т. Д.
- Скрыть все решения / шаги / и т. Д.
- Разделы
- Площадь между кривыми
- Объемы твердых тел вращения / Метод цилиндров
- Разделы
- Интегралы
- Дополнительно
- Классы
Алгебра
- Исчисление I
Исчисление II
Исчисление III
Дифференциальные уравнения
- Дополнительно
Алгебра и триггерный обзор
Распространенные математические ошибки
Праймер для комплексных чисел
Как изучать математику
Шпаргалки и таблицы
- Разное
- Свяжитесь со мной
- Справка и настройка MathJax
- Мои студенты
- Заметки Загрузки
- Полная книга
- Текущая глава
- Текущий раздел
- Practice Problems Загрузок
- Полная книга — Только проблемы
- Полная книга — Решения
- Текущая глава — Только проблемы
- Текущая глава — Решения
- Текущий раздел — Только проблемы
- Текущий раздел — Решения
- Проблемы с назначением Загрузок
- Полная книга
- Текущая глава
- Текущий раздел
- Прочие товары
- Получить URL для загружаемых элементов
- Распечатать страницу в текущем виде (по умолчанию)
- Показать все решения / шаги и распечатать страницу
- Скрыть все решения / шаги и распечатать страницу
- Дом
- Классы
- Алгебра
- Предварительные мероприятия
- Целочисленные экспоненты
- Рациональные экспоненты
- Радикалы
- Полиномы
- Факторинговые многочлены
- Рациональные выражения
- Комплексные числа
- Решение уравнений и неравенств
- Решения и наборы решений
- Линейные уравнения
- Приложения линейных уравнений
- Уравнения с более чем одной переменной
- Квадратные уравнения — Часть I
- Квадратные уравнения — Часть II
- Квадратные уравнения: сводка
- Приложения квадратных уравнений
- Уравнения, сводимые к квадратичным в форме
- Уравнения с радикалами
- Линейные неравенства
- Полиномиальные неравенства
- Рациональные неравенства
- Уравнения абсолютных значений
- Предварительные мероприятия
.
Как рассчитать концентрации при приготовлении разбавлений
- Образование
- Наука
- Химия
- Как рассчитать концентрации при приготовлении разбавлений
Питер Дж. Микулецки, Крис Хрен
Реальные химики в реальной жизни лаборатории не делают все решения с нуля. Вместо этого они делают концентрированные исходных растворов , а затем делают разведения из этих исходных растворов по мере необходимости для данного эксперимента.
Чтобы сделать разбавление, вы просто добавляете небольшое количество концентрированного исходного раствора к количеству чистого растворителя. Полученный раствор содержит количество растворенного вещества, первоначально взятого из исходного раствора, но диспергирует это растворенное вещество по большему объему. Следовательно, конечная концентрация ниже; конечный раствор менее концентрированный и более разбавленный.
Как узнать, какое количество исходного раствора использовать и какое количество чистого растворителя использовать? Это зависит от концентрации исходного раствора, а также от концентрации и объема конечного раствора, который вы хотите.Вы можете ответить на подобные насущные вопросы, используя уравнение разбавления, которое связывает концентрацию (C) и объем ( V ) между начальным и конечным состояниями:
C 1 V 1 = C 2 V 2
Вы можете использовать уравнение разбавления с любыми единицами концентрации, при условии, что вы используете одни и те же единицы во всех расчетах.Поскольку молярность является распространенным способом выражения концентрации, уравнение разбавления иногда выражается следующим образом, где M 1 и M 2 относятся к начальной и конечной молярности, соответственно:
M 1 V 1 = M 2 V 2
Например, , как приготовить 500 мл 0,200 M NaOH ( водн. ) из исходного раствора 1.5 M NaOH?
Начните с использования уравнения разбавления,
M 1 V 1 = M 2 V 2
Начальная молярность M 1 происходит от исходного раствора и, следовательно, составляет 1,5 M . Конечная молярность — это та молярность, которую вы хотите получить в своем окончательном растворе, которая составляет 0,200 M . Последний объем — тот, который вам нужен для окончательного решения, 500.мл, что эквивалентно 0,500 л. Используя эти известные значения, вы можете рассчитать начальный объем: В 1 :
Расчетный объем эквивалентен 67 мл. Конечный объем водного раствора должен составлять 500 мл, из которых 67 мл приходится на исходный раствор. Остальное, 500 мл — 67 мл = 433 мл, поступает из чистого растворителя (в данном случае воды). Итак, чтобы приготовить раствор, добавьте 67 мл исходного раствора 1,5 M к 433 мл воды .Смешайте и наслаждайтесь!
T Другая проблема: Какова конечная молярная концентрация раствора, полученного разбавлением 2,50 мл 3,00 M KCl ( водн. ) до конечного объема 0,175 л?
Вы можете использовать уравнение разбавления,
M 1 V 1 = M 2 V 2
В этой задаче начальная молярность равна 3.00 M , начальный объем составляет 2,50 мл или 2,50 x 10 –3 л, а конечный объем составляет 0,175 л. Используйте эти известные значения для расчета окончательной молярности, M 2 :
Итак, конечная молярная концентрация раствора составляет
4,29 x 10 –2 M
Об авторе книги
Кристофер Хрен — учитель химии в средней школе, бывший тренер по легкой атлетике и футболу. Питер Дж. Микулеки, доктор философии, преподает биологию и химию в Учебном центре Fusion и Академии Fusion.
.
Исчисление I — Дополнительные задачи по объему
Онлайн-заметки Павла
Заметки
Быстрая навигация
Скачать
- Перейти к
- Заметки
Проблемы с практикой
Проблемы с назначением
- Показать / Скрыть
- Показать все решения / шаги / и т. Д.
- Скрыть все решения / шаги / и т. Д.
- Разделы
- Объемы твердых тел вращения / Метод цилиндров
- Работа
- Разделы
- Интегралы
- Дополнительно
- Классы
Алгебра
- Исчисление I
Исчисление II
Исчисление III
Дифференциальные уравнения
- Дополнительно
Алгебра и триггерный обзор
Распространенные математические ошибки
Праймер для комплексных чисел
Как изучать математику
Шпаргалки и таблицы
- Разное
- Свяжитесь со мной
- Справка и настройка MathJax
- Мои студенты
- Заметки Загрузки
- Полная книга
- Текущая глава
- Текущий раздел
- Practice Problems Загрузок
- Полная книга — Только проблемы
- Полная книга — Решения
- Текущая глава — Только проблемы
- Текущая глава — Решения
- Текущий раздел — Только проблемы
- Текущий раздел — Решения
- Проблемы с назначением Загрузок
- Полная книга
- Текущая глава
- Текущий раздел
- Прочие товары
- Получить URL для загружаемых элементов
- Распечатать страницу в текущем виде (по умолчанию)
- Показать все решения / шаги и распечатать страницу
- Скрыть все решения / шаги и распечатать страницу
- Дом
- Классы
- Алгебра
- Предварительные мероприятия
- Целочисленные экспоненты
- Рациональные экспоненты
- Радикалы
- Полиномы
- Факторинговые многочлены
- Рациональные выражения
- Комплексные числа
- Решение уравнений и неравенств
- Решения и наборы решений
- Линейные уравнения
- Приложения линейных уравнений
- Уравнения с более чем одной переменной
- Квадратные уравнения — Часть I
- Квадратные уравнения — Часть II
- Квадратные уравнения: сводка
- Приложения квадратных уравнений
- Уравнения, сводимые к квадратичным в форме
- Уравнения с радикалами
- Линейные неравенства
- Полиномиальные неравенства
- Рациональные неравенства
- Уравнения абсолютных значений
- Предварительные мероприятия
.
