Модуль упругости стали в лире: Страница не найдена
- Lira Учебное пособие — Стр 18
- Приложение 3 физические характеристики материалов
- Расчёт рамы в Лире — Оптимизация сечений
- Модуль упругости стали и других материалов
- Модуль упругости для стали, а также для других материалов
- Модули упругости и коэффициенты Пуассона для некоторых материалов 013
- Модуль упругости Юнга для металлов и сплавов
- Эластичность, упругие свойства
- Что такое модуль упругости? (с рисунками)
- МЕХАНИЧЕСКИЕ СВОЙСТВА МЕТАЛЛОВ И СПЛАВОВ
Lira Учебное пособие — Стр 18
ПРИМЕР 7. Нелинейный расчет двухпролетной балки с учетом ползучести бетона
Формирование типов жесткости
С помощью меню
Жесткости Жесткости элементов (кнопка на панели инструментов) вызовите диалоговое окно
Жесткости элементов
(рис.7.11).
В этом окне щелкните по кнопке Добавить для того, чтобы вывести список стандартных типов сечений.
Выберите двойным щелчком мыши на элементе графического списка тип сечения Тавр_Т.
В диалоговом окне Задание
стандартного сечения
(рис.7.12) задайте
параметры сечения Тавр_Т: | Рис.7.11 Диалоговое окно Жесткости элементов |
|
геометрические размеры – В = 30 см;
Н = 60 см; В1 = 70 см; Н1 = 20 см;
удельный вес материала – Rо = 2. 75 т/м3.
75 т/м3.
Далее установите флажок Учет нелинейности.
Для задания материала щелкните по кнопке Параметры материала.
Вызывается диалоговое окно
Законы нелинейного деформирования материалов
(рис.7.13).
В этом окне, для основного материала, в раскрывающемся списке Закон нелинейного деформирования выберите строку 25 – экспоненциальный
(нормативная прочность) закон деформирования.
В таблице Параметры закона нелинейного деформирования,
после двойного щелчка по ячейке значений задайте параметры основного материала (бетона):
класс бетона – В25; тип бетона – ТБ.
Рис.7.12 Диалоговое окно
Задание стандартного сечения
© 2011 ЛИРА САПР 2011 | 171 |
ПК ЛИРА–САПР 2011. Учебное пособие
Рис.7.13 Диалоговое окно Законы нелинейного деформирования материалов
для основного материала
Далее в этом же окне установите флажок Учитывать армирующий материал (рис. 7.14) и перейдите на закладку Армирующий материал.
7.14) и перейдите на закладку Армирующий материал.
В раскрывающемся списке Закон нелинейного деформирования выберите строку 11 –
экспоненциальный закон деформирования.
В таблице Параметры закона нелинейного деформирования задайте следующие параметры (при английской раскладке клавиатуры):
модуль упругости – Ео(-) = 2е7 т/м2;
модуль упругости – Ео(+) = 2е7 т/м2;
| предельное напряжение | (-) = -36000 т/м2; |
| предельное напряжение | (+) = 36000 т/м2. |
172 | © 2011 ЛИРА САПР 2011 |
ПРИМЕР 7. Нелинейный расчет двухпролетной балки с учетом ползучести бетона
Рис.7.14 Диалоговое окно Законы нелинейного деформирования материалов
для армирующего материала
Далее в этом же окне установите флажок Учитывать ползучесть бетона (рис. 7.15) и перейдите на закладку Ползучесть бетона.
7.15) и перейдите на закладку Ползучесть бетона.
В раскрывающемся списке Закон ползучести бетона выберите строку 41 – степенной закон ползучести (EuroCode prEN 1992-1-1).
В таблице Параметры закона нелинейного деформирования задайте следующие параметры:
теоретический коэффициент ползучести – φо =2;
коэффициент – βH =657.82.
Для ввода данных щелкните по кнопке Подтвердить.
Рис.7.15 Диалоговое окно Законы нелинейного деформирования материалов
для ползучести бетона
© 2011 ЛИРА САПР 2011 | 173 |
ПК ЛИРА–САПР 2011. Учебное пособие
Для задания расположения и площади арматуры, в диалоговом окне Задание стандартного сечения (рис.7.12) щелкните по кнопке Параметры арматуры. Вызывается диалоговое окно
Характеристики физической нелинейности стержней (рис.7.16).
В этом окне, для выбора арматурных включений, щелкните по кнопке Точечная арматура.
Задайте параметры арматуры для первого слоя арматуры:
площадь арматуры – Fa = 6 см2;
координаты привязки – у = 0 см; z = 6 см.
В раскрывающемся списке Номер слоя арматуры выберите номер 2.
Задайте параметры арматуры для второго слоя арматуры:
площадь арматуры – Fa = 1.5 см2;
координаты привязки – у = 0 см; z = 54 см.
Для выбора типа дробления поперечного сечения, щелкните по кнопке Дробление на
элементарные полосы.
Чтобы увидеть эскиз сечения щелкните по кнопке Нарисовать.
Для ввода данных щелкните по кнопке Подтвердить.
Рис.7.16 Диалоговое окно Характеристики физической нелинейности стержней
После этого в диалоговом окне Задание стандартного сечения щелкните по кнопке –
Подтвердить.
В диалоговом окне Жесткости элементов (рис.7.11) в cписке типов жесткостей с помощью курсора выделите строку 1*.Тавр_Т 30х60 и щелкните по кнопке Копирование.
После этого в списке типов жесткостей выделите строку 2*. Тавр_Т 30х60 и щелкните по кнопке Изменить.
Тавр_Т 30х60 и щелкните по кнопке Изменить.
174 | © 2011 ЛИРА САПР 2011 |
ПРИМЕР 7. Нелинейный расчет двухпролетной балки с учетом ползучести бетона
В диалоговом окне Задание стандартного сечения щелкните по кнопке Параметры арматуры. Вызывается диалоговое окно Характеристики физической нелинейности стержней (рис.7.17).
В закладке Тип арматурных включений выбран тип Точечная арматура.
Задайте параметры арматуры для первого слоя арматуры:
площадь арматуры – Fa = 1.5 см2;
координаты привязки – у = 0 см; z = 6 см.
В раскрывающемся списке Номер слоя арматуры выберите номер 2.
Задайте параметры арматуры для второго слоя арматуры:
площадь арматуры – Fa = 9 см2;
координаты привязки – у = 0 см; z = 54 см.
Для ввода данных щелкните по кнопке Подтвердить.
Рис.7.17 Диалоговое окно Характеристики физической нелинейности стержней
После этого в диалоговом окне Задание стандартного сечения щелкните по кнопке –
Подтвердить.
© 2011 ЛИРА САПР 2011 | 175 |
ПК ЛИРА–САПР 2011. Учебное пособие
Смена типа конечных элементов
Выполните пункт меню Выбор Отметка горизонтальных элементов (кнопка на панели инструментов).
С помощью курсора выделите все элементы балки.
Выполните пункт меню Схема Корректировка Смена типа конечного элемента (кнопка на панели инструментов).
В диалоговом окне Смена типа конечного элемента
(рис.7.18) с помощью курсора выделите строку
Тип 210 – физически нелинейный универсальный пространственный стержневой КЭ.
Щелкните по кнопке – Применить.
Рис.7.18 Диалоговое окно
Смена типа конечного элемента
Назначение жесткостей элементам балки
Выполните пункт меню Жесткости Жесткости элементов (кнопка на панели инструментов).
В диалоговом окне Жесткости элементов в списке типов жесткостей выделите курсором тип жесткости 1*. Тавр_Т 30х60.
Тавр_Т 30х60.
Щелкните по кнопке Установить как текущий тип (при этом выбранный тип записывается в окне редактирования Текущий тип жесткости. Можно назначить текущий тип жесткости двойным щелчком на строке списка).
С помощью курсора выделите элементы № 1, 2, 3, 6, 7 и 8.
В диалоговом окне Жесткости элементов щелкните по кнопке Назначить.
В диалоговом окне Жесткости элементов в списке типов жесткостей выделите курсором тип жесткости 2*.Тавр_Т 30х60.
Щелкните по кнопке Установить как текущий тип.
С помощью курсора выделите элементы № 4 и 5.
В диалоговом окне Жесткости элементов щелкните по кнопке Назначить.
Этап 5. Задание нагрузок
Формирование загружения № 1
Выполните пункт меню Нагрузки Добавить собственный вес.
В диалоговом окне Добавить собственный вес (рис.7.19), при включенной радио-кнопке все элементы и заданном коэф. надежности по нагрузке равном 1, щелкните по кнопке – Применить.
Рис.7. 19 Диалоговое окно
19 Диалоговое окно
Добавить собственный вес
176 | © 2011 ЛИРА САПР 2011 |
ПРИМЕР 7. Нелинейный расчет двухпролетной балки с учетом ползучести бетона
Формирование загружения № 2
Смените номер текущего загружения, вызвав диалоговое окно Активное загружение (рис.7.20) с помощью меню Нагрузки Выбор загружения
(кнопка на панели инструментов).
В этом диалоговом окне задайте номер загружения 2.
|
| Рис.7.20 Диалоговое окно |
Щелкните по кнопке | – Подтвердить. | Активное загружение |
Выделите все элементы.
Вызовите диалоговое окно Задание нагрузок (рис.7.21) с помощью меню Нагрузки Нагрузка на узлы и элементы (кнопка на панели инструментов).
В этом окне перейдите на закладку Нагрузки на стержни (по умолчанию указана система координат Глобальная, направление – вдоль оси Z).
Щелчком по кнопке равномерно распределенной нагрузки вызовите диалоговое окно Параметры.
В этом окне задайте интенсивность нагрузки р = 0.3 т/м (рис.7.22).
Щелкните по кнопке – Подтвердить.
После этого в диалоговом окне Задание нагрузок
щелкните по кнопке – Применить.
Рис.7.21 Диалоговое окно | Рис.7.22 Диалоговое окно Параметры |
Задание нагрузок |
|
Формирование загружения № 3
Смените номер текущего загружения, вызвав диалоговое окно Активное загружение с
помощью меню Нагрузки Выбор загружения (кнопка на панели инструментов).
В этом диалоговом окне смените номер загружения на 3.
Щелкните по кнопке – Подтвердить.
С помощью курсора выделите элементы первого пролета № 1, 2, 3 и 4.
© 2011 ЛИРА САПР 2011 | 177 |
ПК ЛИРА–САПР 2011. Учебное пособие
Учебное пособие
В диалоговом окне Задание нагрузок щелчком по кнопке равномерно распределенной нагрузки вызовите диалоговое окно Параметры.
В этом окне задайте интенсивность нагрузки р = 0.87 т/м.
Щелкните по кнопке – Подтвердить.
После этого в диалоговом окне Задание нагрузок щелкните по кнопке – Применить.
Формирование загружения № 4
Смените номер текущего загружения, вызвав диалоговое окно Активное загружение с
помощью меню Нагрузки Выбор загружения (кнопка на панели инструментов).
В этом диалоговом окне смените номер загружения на 4.
Щелкните по кнопке – Подтвердить.
С помощью курсора выделите элементы второго пролета № 5, 6, 7 и 8.
В диалоговом окне Задание нагрузок щелкните по кнопке – Применить.
Этап 6. Моделирование нелинейных загружений с учетом ползучести бетона
Для того чтобы получить расчет балки с полезной нагрузкой в разных пролетах необходимо выполнить две последовательности приложения нагрузок.
Формирование первой последовательности
Чтобы получить первую последовательность 1, 2 и 3 загружения (полезная нагрузка в первом пролете), с помощью пункта меню Нагрузки Моделирование нелинейных загружений
(кнопка на панели инструментов) вызовите диалоговое окно Моделирование нелинейных загружений конструкции (рис.7.23).
В этом окне для создания первой последовательности приложения нагрузок щелкните по кнопке – Добавить (в левой части окна в поле История добавляется первая история нагружений и автоматически выделяется строка загружения обозначенная знаком вопроса).
Далее для первого загружения задайте следующие параметры:
№ загружения – 1;
в раскрывающемся списке Метод расчета выберите строку (1) Простой шаговый;
включите радио-кнопку Равномерные шаги и задайте количество шагов 5;
в раскрывающемся списке Печать выберите строку Перемещения и усилия после каждого шага.
Щелкните по кнопке – Применить.
178 | © 2011 ЛИРА САПР 2011 |
ПРИМЕР 7. Нелинейный расчет двухпролетной балки с учетом ползучести бетона
Нелинейный расчет двухпролетной балки с учетом ползучести бетона
Рис.7.23 Диалоговое окно Моделирование нелинейных загружений конструкции
После этого, для того чтобы добавить строки задания параметров второго и третьего загружений, при выделенной строке первого загружения дважды щелкните по кнопке –
Добавить.
Затем с помощью курсора мыши выделите вторую строку загружения, которая обозначена знаком вопроса и задайте следующие параметры:
№ загружения – 2;
в раскрывающемся списке Метод расчета выберите строку (1) Простой шаговый;
при включенной радио-кнопке Равномерные шаги задайте количество шагов 30;
в раскрывающемся списке Печать выберите строку Перемещения и усилия после каждого шага.
Щелкните по кнопке – Применить.
Далее выделите третью строку загружения, которая обозначена знаком вопроса и задайте следующие параметры:
№ загружения – 3;
в раскрывающемся списке Метод расчета выберите строку (1) Простой шаговый;
при включенной радио-кнопке Равномерные шаги задайте количество шагов 30;
в раскрывающемся списке Печать выберите строку Перемещения и усилия после каждого шага.
Щелкните по кнопке – Применить.
Формирование второй последовательности
Чтобы получить вторую последовательность 1, 2 и 4 загружения (полезная нагрузка во
втором пролете), в диалоговом окне Моделирование нелинейных загружений
© 2011 ЛИРА САПР 2011 | 179 |
ПК ЛИРА–САПР 2011. Учебное пособие
конструкции (рис.7.24) в поле История выделите первую историю нагружений и щелкните по кнопке – Добавить.
Далее при выделенной строке обозначенной знаком вопроса задайте следующие параметры:
№ загружения – 1;
в раскрывающемся списке Метод расчета выберите строку (1) Простой шаговый;
при включенной радио-кнопке Равномерные шаги задайте количество шагов 5;
в раскрывающемся списке Печать выберите строку Перемещения и усилия после каждого шага.
Щелкните по кнопке – Применить.
Рис.7.24 Диалоговое окно Моделирование нелинейных загружений конструкции
После этого, для того чтобы добавить строки задания параметров второго и четвертого загружений, при выделенной строке первого загружения второй истории нагружений дважды щелкните по кнопке – Добавить.
Затем выделите вторую строку загружения, которая обозначена знаком вопроса и задайте следующие параметры:
№ загружения – 2;
в раскрывающемся списке Метод расчета выберите строку (1) Простой шаговый;
при включенной радио-кнопке Равномерные шаги задайте количество шагов 30;
в раскрывающемся списке Печать выберите строку Перемещения и усилия после каждого шага.
Щелкните по кнопке – Применить.
180 | © 2011 ЛИРА САПР 2011 |
Приложение 3 физические характеристики материалов
Таблица
63
Физические характеристики
материалов для стальных конструкций
Характеристика | Значение |
Плотность |
|
проката и стальных отливок | 7850 |
отливок из чугуна | 7200 |
Коэффициент | 0,12 · 10-4 |
Модуль |
|
прокатной стали и стальных отливок | 2,06 · 105 |
отливок из чугуна марок: |
|
СЧ15 | 0,83 · 105 |
СЧ20, СЧ25, СЧ30 | 0,98 · 105 |
пучков и прядей параллельных | 1,96 · 105 |
канатов стальных: |
|
спиральных и закрытых несущих | 1,67 · 105 |
двойной свивки | 1,47 · 105 |
двойной свивки с неметаллическим | 1,27 · 105 |
Модуль | 0,78 |
Коэффициент | 0,3 |
Примечание.
Значения модуля упругости даны для
канатов, предварительно вытянутых
усилием не менее 60 % разрывного усилия
для каната в целом.
Таблица
64
Физические характеристики
проводов и проволоки
Наименование материалов | Марка и | Модуль | Коэффициент |
Алюминиевые | А, АКП; | 0,630 · 105 | 0,23 · 10-4 |
Медные | М; 4-800 | 1,300 · 105 | 0,17 · 10-4 |
Сталеалюминиевые | АС, АСК; |
|
|
6-6,25 | 10 и более | 0,825 · 105 | 0,192 · 10-4 |
0,65 | 95 | 1,460 · 105 | 0,139 · 10-4 |
4,29-4,39 | 120 и более | 0,890 · 105 | 0,183 · 10-4 |
7,71-8,04 | 150 и более | 0,770 · 105 | 0,198 · 10-4 |
1,46 | 185 и более | 1,140 · 105 | 0,155 · 10-4 |
12,22 | 330 | 0,665 · 105 | 0,212 · 10-4 |
18,2-18,5 | 400 и 500 | 0,665 · 105 | 0,212 · 10-4 |
Биметаллическая | БСМ 1 |
|
|
1,6-4 | 2,0-12,5 | 1,870 · 105 | 0,127 · 10-4 |
6 | 28,2 | 1,900 · 105 | 0,124 · 10-4 |
Примечание.
Значение массы проводов и проволоки
следует принимать по ГОСТ
839-80*Е и ГОСТ
3822-79*.
Расчёт рамы в Лире — Оптимизация сечений
В прошлой статье Расчёт рамы в Лире ч.5 — Прочностной расчёт мы подобрали сечения, теперь попробуем их оптимизировать.
Оптимизация конструкции
Несмотря на то, что решение в принципе рабочее, возможно оно не вполне обосновано экономически. Наша дальнейшая задача проработать другие варианты конструкции, чтобы она была как можно меньше по стоимости. Начнем мы оптимизацию с балки.
Есть несколько вариантов оптимизации:
1) Изменить схему (например ввести дополнительную стойку по центру, изменить закрепление с колонной и т.д.). В рамках этой задачи мы не будем пока этим заниматься, но в дальнейшем сравним схемы с другими;
2) Изменить сортамент металлопроката. Т.к. у нас сечение балки подбирается по изгибающему моменту, то если поменять профиль на профиль имеющий примерно такой же момент сопротивления сечения (Wx), при этом имеющую массу меньше, то скорее всего это будет экономичнее (необходимо еще проверить на прогиб и другие параметры).
3) Увеличить марку стали. Марка стали у нас принята минимально требуемая С245, но мы же можем увеличить её. Тогда при увеличении прочности стали уменьшится профиль и, соответственно расход стали и нагрузки от веса балки на нижележащие конструкции. Конечно более прочная марка стали будет дороже, но для изгибаемых элементов это, как правило, оправданно.
Таблица результатов
Чтобы понять какой метод оптимизации нам подходит или не подходит необходимо просмотреть по каким параметрам программа подобрала нам белку. Т.е. что является критическим при подборе. Для этого нам необходимо просмотреть таблицу результатов для наших элементов.
Проверка подбора балки
С помощью команды Отметка элементов выбираем все элементы балки (от 5 до 12) и по вкладке Конструирование жмем на кнопку Документация -> Таблица результатов для стали.
Выбираем Проверка и нажимаем на Зеленую галочку
Получаем следующую таблицу:
Балки
| Элемент | НС | Группа | Шаг ребер, м | Фb min | Проценты исчерпания несущей способности балки по сечениям, % | Длина элемента, м | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| нор | тау | с1 | УБ | Прг | УС | УП | 1ПС | 2ПС | М. У У | ||||||
| Сечение: 2.1.1. Двутавр 55Б1 | |||||||||||||||
| Профиль: 55Б1; СТО АСМЧ 20-93 | |||||||||||||||
| Сталь: ВСт3Гпс5; ГОСТ 380-71* | |||||||||||||||
| Сортамент: СТО АСМЧ 20-93. Нормальные двутавры | |||||||||||||||
| 5 | 1 | КБ1 | 0.00 | 1.00 | 0 | 16 | 11 | 0 | 92 | 52 | 0 | 16 | 92 | 52 | 6.03 |
| 5 | 2 | КБ1 | 0.00 | 1.00 | 8 | 16 | 12 | 0 | 92 | 52 | 33 | 16 | 92 | 52 | 6.03 |
| 5 | 3 | КБ1 | 0.00 | 1.00 | 15 | 16 | 16 | 0 | 92 | 52 | 33 | 16 | 92 | 52 | 6.03 |
| 5 | 4 | КБ1 | 0.00 | 1.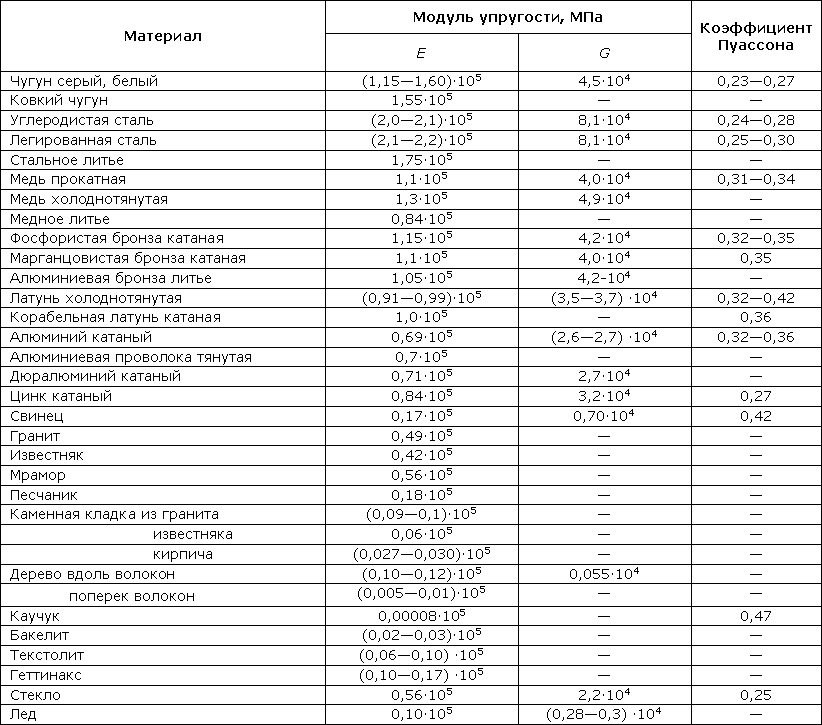 00 00 | 23 | 16 | 20 | 0 | 92 | 52 | 33 | 23 | 92 | 52 | 6.03 |
| 5 | 5 | КБ1 | 0.00 | 1.00 | 31 | 16 | 25 | 0 | 92 | 52 | 33 | 31 | 92 | 52 | 6.03 |
| 6 | 1 | КБ1 | 0.00 | 1.00 | 31 | 11 | 24 | 0 | 92 | 52 | 33 | 31 | 92 | 52 | 6.03 |
| 6 | 2 | КБ1 | 0.00 | 1.00 | 36 | 11 | 28 | 0 | 92 | 52 | 33 | 36 | 92 | 52 | 6.03 |
| 6 | 3 | КБ1 | 0.00 | 1.00 | 42 | 11 | 32 | 0 | 92 | 52 | 33 | 42 | 92 | 52 | 6. 03 03 |
| 6 | 4 | КБ1 | 0.00 | 1.00 | 47 | 11 | 36 | 0 | 92 | 52 | 33 | 47 | 92 | 52 | 6.03 |
| 6 | 5 | КБ1 | 0.00 | 1.00 | 53 | 11 | 40 | 0 | 92 | 52 | 33 | 53 | 92 | 52 | 6.03 |
| 7 | 1 | КБ1 | 0.00 | 1.00 | 53 | 7 | 40 | 0 | 92 | 52 | 33 | 53 | 92 | 52 | 6.03 |
| 7 | 2 | КБ1 | 0.00 | 1.00 | 56 | 7 | 42 | 0 | 92 | 52 | 33 | 56 | 92 | 52 | 6.03 |
| 7 | 3 | КБ1 | 0.00 | 1.00 | 59 | 7 | 45 | 0 | 92 | 52 | 33 | 59 | 92 | 52 | 6.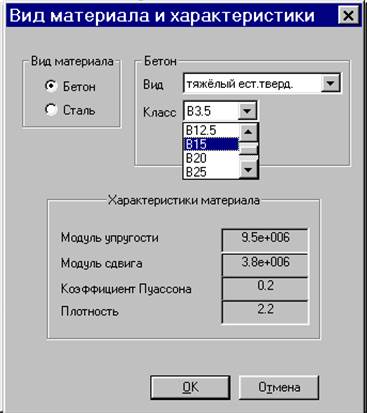 03 03 |
| 7 | 4 | КБ1 | 0.00 | 1.00 | 63 | 7 | 47 | 0 | 92 | 52 | 33 | 63 | 92 | 52 | 6.03 |
| 7 | 5 | КБ1 | 0.00 | 1.00 | 66 | 7 | 50 | 0 | 92 | 52 | 33 | 66 | 92 | 52 | 6.03 |
| 8 | 1 | КБ1 | 0.00 | 1.00 | 66 | 2 | 49 | 0 | 92 | 52 | 33 | 66 | 92 | 52 | 6.03 |
| 8 | 2 | КБ1 | 0.00 | 1.00 | 67 | 2 | 50 | 0 | 92 | 52 | 33 | 67 | 92 | 52 | 6.03 |
| 8 | 3 | КБ1 | 0.00 | 1.00 | 68 | 2 | 51 | 0 | 92 | 52 | 34 | 68 | 92 | 52 | 6. 03 03 |
| 8 | 4 | КБ1 | 0.00 | 1.00 | 69 | 2 | 52 | 0 | 92 | 52 | 34 | 69 | 92 | 52 | 6.03 |
| 8 | 5 | КБ1 | 0.00 | 1.00 | 70 | 2 | 53 | 0 | 92 | 52 | 34 | 70 | 92 | 52 | 6.03 |
| 9 | 1 | КБ2 | 0.00 | 1.00 | 0 | 16 | 11 | 0 | 92 | 52 | 0 | 16 | 92 | 52 | 6.03 |
| 9 | 2 | КБ2 | 0.00 | 1.00 | 8 | 16 | 12 | 0 | 92 | 52 | 33 | 16 | 92 | 52 | 6.03 |
| 9 | 3 | КБ2 | 0.00 | 1.00 | 15 | 16 | 16 | 0 | 92 | 52 | 33 | 16 | 92 | 52 | 6. 03 03 |
| 9 | 4 | КБ2 | 0.00 | 1.00 | 23 | 16 | 20 | 0 | 92 | 52 | 33 | 23 | 92 | 52 | 6.03 |
| 9 | 5 | КБ2 | 0.00 | 1.00 | 31 | 16 | 25 | 0 | 92 | 52 | 33 | 31 | 92 | 52 | 6.03 |
| 10 | 1 | КБ2 | 0.00 | 1.00 | 31 | 11 | 24 | 0 | 92 | 52 | 33 | 31 | 92 | 52 | 6.03 |
| 10 | 2 | КБ2 | 0.00 | 1.00 | 36 | 11 | 28 | 0 | 92 | 52 | 33 | 36 | 92 | 52 | 6.03 |
| 10 | 3 | КБ2 | 0.00 | 1.00 | 42 | 11 | 32 | 0 | 92 | 52 | 33 | 42 | 92 | 52 | 6. 03 03 |
| 10 | 4 | КБ2 | 0.00 | 1.00 | 47 | 11 | 36 | 0 | 92 | 52 | 33 | 47 | 92 | 52 | 6.03 |
| 10 | 5 | КБ2 | 0.00 | 1.00 | 53 | 11 | 40 | 0 | 92 | 52 | 33 | 53 | 92 | 52 | 6.03 |
| 11 | 1 | КБ2 | 0.00 | 1.00 | 53 | 7 | 40 | 0 | 92 | 52 | 33 | 53 | 92 | 52 | 6.03 |
| 11 | 2 | КБ2 | 0.00 | 1.00 | 56 | 7 | 42 | 0 | 92 | 52 | 33 | 56 | 92 | 52 | 6.03 |
| 11 | 3 | КБ2 | 0.00 | 1.00 | 59 | 7 | 45 | 0 | 92 | 52 | 33 | 59 | 92 | 52 | 6. 03 03 |
| 11 | 4 | КБ2 | 0.00 | 1.00 | 63 | 7 | 47 | 0 | 92 | 52 | 33 | 63 | 92 | 52 | 6.03 |
| 11 | 5 | КБ2 | 0.00 | 1.00 | 66 | 7 | 50 | 0 | 92 | 52 | 33 | 66 | 92 | 52 | 6.03 |
| 12 | 1 | КБ2 | 0.00 | 1.00 | 66 | 2 | 49 | 0 | 92 | 52 | 33 | 66 | 92 | 52 | 6.03 |
| 12 | 2 | КБ2 | 0.00 | 1.00 | 67 | 2 | 50 | 0 | 92 | 52 | 33 | 67 | 92 | 52 | 6.03 |
| 12 | 3 | КБ2 | 0.00 | 1.00 | 68 | 2 | 51 | 0 | 92 | 52 | 34 | 68 | 92 | 52 | 6. 03 03 |
| 12 | 4 | КБ2 | 0.00 | 1.00 | 69 | 2 | 52 | 0 | 92 | 52 | 34 | 69 | 92 | 52 | 6.03 |
| 12 | 5 | КБ2 | 0.00 | 1.00 | 70 | 2 | 53 | 0 | 92 | 52 | 34 | 70 | 92 | 52 | 6.03 |
Пояснения что означают обозначения в таблице можно посмотреть нажав в программа F1 и пройды по ссылке Таблица результатов (пояснения) или в таблице ниже:
Таблицы результатов (пояснения)
ЭЛЕМЕНТ | Номер конечного элемента |
НC | Номер сечения по длине конечного элемента |
ГРУППА | Группа унификации элемента, конструктивный элемент |
ШАГ РЕБЕР (РЕШЕТКИ) | Шаг поперечных ребер жесткости или соединительной решетки (планок — в свету) |
ШАГ ПЛАНОК | Шаг поперечных соединительных планок в свету |
Фb min | Минимальный коэффициент поперечного изгиба |
Далее следуют проценты исчерпания несущей способности по проверкам СНиП: | |
нор | нормальные напряжения |
тау | касательные напряжения |
с1 | приведенные напряжения |
УБ | общая устойчивость балки |
УY1 | устойчивость относительно оси Y1 |
УZ1 | устойчивость относительно оси Z1 |
УYZ | устойчивость колонны, сжатой в 2-х плоскостях |
ГY1 | предельная гибкость относительно оси Y1 |
ГZ1 | предельная гибкость относительно оси Z1 |
Г>Г* | Соотношение гибкостей или прогиб. В колонне с решеткой – большее из двух отношений: гибкости сквозной колонны к гибкости ветви на участке между узлами или гибкости ветви на участке между узлами к 80. max(lef / l, l /80) В колонне с планками – отношение гибкости ветви к 40: l / 40 В балке – прогиб. |
УС | местная устойчивость стенки |
УП | местная устойчивость сжатого пояса |
Прг | относительный прогиб балки |
1ПС | Сводный процент использования сечения по 1-му предельному состоянию |
2ПС | Сводный процент использования сечения по 2-му предельному состоянию |
М.У | Сводный процент использования сечения по местной устойчивости |
ДЛИНА ЭЛЕМЕНТ | Геометрическая длина конструктивного элемента |
Как видим критическим фактором в нашем случае является прогиб балки. Прогиб зависит от нагрузки, модуля упругости и момента инерции сечения. Однако более оптимального профиля, который имел бы необходимый момент инерции сечения и при этом весил бы меньше, я не нашел. Поэтому оставляем профиль для балки 55Б1.
Прогиб зависит от нагрузки, модуля упругости и момента инерции сечения. Однако более оптимального профиля, который имел бы необходимый момент инерции сечения и при этом весил бы меньше, я не нашел. Поэтому оставляем профиль для балки 55Б1.
Изменять марку стали на более прочную не имеет смысла т.к. прогиб из-за этого не измениться, а запас по прочности у нас и так 30%.
Проверка подбора колонны
Далее проверим колонну. Тут складывается интересная ситуация. Если мы попробуем подобрать профиль, то нам программа посоветует выбрать профиль 20К1
Как же так получилось, что изначально профиль не подходил, а теперь после замены профиля балки, профиль 20К1 для колонны стал подходить? Я сравнил напряжения в этих 2-х случаях и заметил, что до замены профиля балки изгибающий момент в колонне был выше, чем после замены балки. Это вызвано деформациями, которые были при использовании профиля балки 20Б1, но при замене профиля на 55Б1 изгибающий момент снизился т. к. уже нет этих деформаций. Поэтому после замены профиля балки профиль колонны также можно изменить на 20К1. Давайте поменяем и проверим.
к. уже нет этих деформаций. Поэтому после замены профиля балки профиль колонны также можно изменить на 20К1. Давайте поменяем и проверим.
Во панели Создание и редактирование, вкладке Жесткости и связи нажимаем на кнопку Жесткости. Выбираем двутавр 25К1 и жмем кнопку Изменить.
Выбираем профиль 20К1 и жмем ОК
Далее в панели Расчёт нажимаем на кнопку Выполнить расчёт. Выбираем колонны с помощью инструмента Отметка элементов и в панели Конструирование во вкладке Документация нажимаем на кнопку Таблица результатов стали. Выбираем Проверка и жмем на зеленую галочку.
Получается следующая таблица:
Колонны
| Элемент | НС | Группа | Шаг решетки (ребер), м | Проценты исчерпания несущей способности колонны по сечениям, % | Длина элемента, м | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| нор | УY1 | УZ1 | УYZ | ГY1 | ГZ1 | УС | УП | 1ПС | 2ПС | М.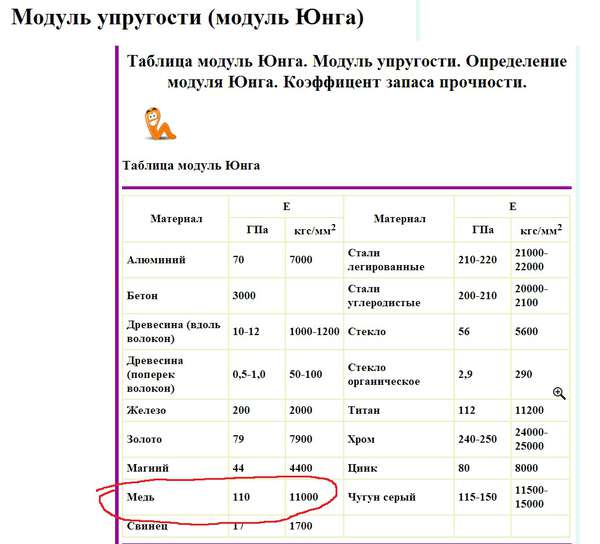 У У | |||||
| Сечение: 1.1.2. Двутавр 20К1 | |||||||||||||||
| Профиль: 20К1; СТО АСЧМ 20-93 | |||||||||||||||
| Сталь: ВСт3Гпс5; ГОСТ 380-71* | |||||||||||||||
| Сортамент: СТО АСЧМ 20-93. Колонные двутавры | |||||||||||||||
| 1 | 1 | 0.00 | 39 | 29 | 42 | 0 | 86 | 73 | 26 | 45 | 42 | 86 | 45 | 5.50 | |
| 1 | 2 | 0.00 | 26 | 27 | 27 | 0 | 86 | 73 | 26 | 45 | 27 | 86 | 45 | 5.50 | |
| 1 | 3 | 0.00 | 14 | 27 | 22 | 0 | 86 | 73 | 26 | 45 | 27 | 86 | 45 | 5.50 | |
| 1 | 4 | 0.00 | 11 | 27 | 21 | 0 | 86 | 73 | 27 | 45 | 27 | 86 | 45 | 5. 50 50 | |
| 1 | 5 | 0.00 | 10 | 27 | 21 | 0 | 86 | 73 | 27 | 30 | 27 | 86 | 30 | 5.50 | |
| 2 | 1 | 0.00 | 42 | 29 | 45 | 0 | 86 | 73 | 26 | 45 | 45 | 86 | 45 | 5.50 | |
| 2 | 2 | 0.00 | 26 | 27 | 27 | 0 | 86 | 73 | 26 | 45 | 27 | 86 | 45 | 5.50 | |
| 2 | 3 | 0.00 | 13 | 27 | 22 | 0 | 86 | 73 | 26 | 45 | 27 | 86 | 45 | 5.50 | |
| 2 | 4 | 0.00 | 11 | 27 | 21 | 0 | 86 | 73 | 27 | 45 | 27 | 86 | 45 | 5. 50 50 | |
| 2 | 5 | 0.00 | 10 | 27 | 21 | 0 | 86 | 73 | 27 | 30 | 27 | 86 | 30 | 5.50 | |
Как видим загрузка колонны 86% по предельной гибкости по оси Z. Пояснения к этой таблице смотрите выше.
Учет эксцентриситета нагрузки
Теперь, когда мы знаем сечение колонны необходимо также добавить эксцентриситет от нагрузки стеновых сэндвич-панелей и основной балки т.к. нагрузка от них приложена не по-центру профиля.
Эксцентриситет от нагрузки веса стеновых панелей вы добавим через равномерно-нагруженную изгибающую нагрузку.
Для начала необходимо выберем нагрузку №1 где мы учитывали вес конструкции, чтобы в него внести корректировки. Для этого на нижней панели убедимся что выбрана нужная нагрузка.
Величину нагрузки считаем следующим образом:
Толщина панели 120 мм, высота профиля колонны 200 мм. Соответственно плечо нагрузки это расстояние между центром профиля и центром панели:
Соответственно плечо нагрузки это расстояние между центром профиля и центром панели:
a=(120+200)/2=160 мм.
Нагрузка от веса панелей: 26 кг/м²*6м=156 кг/м.
Высота 5,5 м.
Изгибающий момент в точке заделки колонны равен: 156*0,16*5,5=137,3 кг*м
К сожалению в моей версии Лиры нет возможности задать равномерно-распределенную изгибающую нагрузку как в SCAD, поэтому я прикладываю изгибающий момент ближе к точке заделки фундамента где изгибающий момент будет максимальный.
Выделяем элемент №1 (левую колонну), нажимаем на кнопку Нагрузка на стержни, ось должна быть Y, и выбираем изгибающий момент на стержень.
Вбиваем высчитанную нагрузку со знаком плюс т.к. у нас нагрузка будет направлена против часовой стрелки и делаем небольшое плечо чтобы мы могли эту нагрузку увидеть на схеме (хотя плечо не имеет значение в данном случае).
Жмем два раза галочку. Если у вас стоит галочка напротив Нагрузки в панели Флаги Рисования (3-я панель), то появится такой значок у колонны.
Далее делаем тоже самое для правой колонны, только нагрузка будет уже со знаком минус
Сохранять нагрузку нет необходимости, она уже сохранилась.
Далее чтобы учесть эксцентриситет нагрузки от балки необходимо добавить жесткую вставку.
Выделяем элементы 5 и 9 (крайние элементы балки) и в панели Стержни жмем кнопку Жесткие вставки стержней
Далее добавляем жесткую вставку размером 0,1м (профиль колонны 200 мм, соответственно от центра колонны до края 100 мм) в узел №1 по оси X.
Жесткая вставка на схеме имеет визуализацию утолщения.
Проводим расчёт и смотрим итоги. Подбор сечения не выдал нам других результатов. А если посмотреть загрузку профиля, то там практически ничего не изменилось. В нашем случае эксцентриситет не повлиял на результаты и можно сказать, что можно рассчитывать схему без его учета добавив его когда будет подобрано сечение колонны.
Далее рассмотрим вариант с шарнирным креплением колонны к фундаменту и жестким креплением к ригелю см.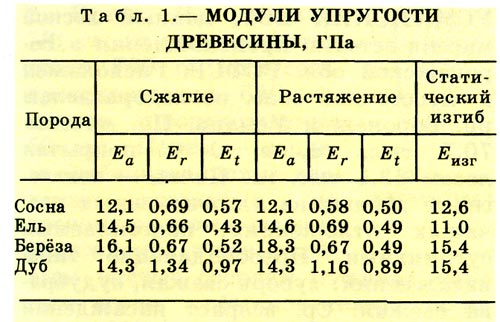 статью Расчёт рамы с жестким закреплением к ригелю ч.1
статью Расчёт рамы с жестким закреплением к ригелю ч.1
Модуль упругости стали и других материалов
Развитие металлургии и других сопутствующих направлений по изготовлению предметов из металла обязано созданию оружия. Сначала научились выплавлять цветные металлы, но прочность изделий была относительно невысокой. Только с появлением железа и его сплавов началось изучение их свойств.
Первые мечи для придания им твердости и прочности делали довольно тяжелыми. Воинам приходилось брать их в обе руки, чтобы управляться с ними. Со временем появились новые сплавы, разрабатывались технологии производства. Легкие сабли и шпаги пришли на замену тяжеловесному оружию. Параллельно создавались орудия труда. С повышением прочностных характеристик совершенствовались инструменты и способы производства.
Виды нагрузок
При использовании металлов прилагаются разные нагрузки статического и динамического воздействия. В теории прочности принято определять нагружения следующих видов.
- Сжатие – действующая сила сдавливает предмет, вызывая уменьшение длины вдоль направления приложения нагрузки. Такую деформацию ощущают станины, опорные поверхности, стойки и ряд других конструкций, выдерживающих определённый вес. Мосты и переправы, рамы автомобилей и тракторов, фундаменты и арматура, – все эти конструктивные элементы находятся при постоянном сжатии.
- Растяжение – нагрузка стремится удлинить тело в определенном направлении. Подъемно-транспортные машины и механизмы испытывают подобные нагружения при подъеме и переноске грузов.
- Сдвиг и срез – такое нагружение наблюдается в случае действия сил, направленных вдоль одной оси навстречу друг другу. Соединительные элементы (болты, винты, заклепки и другие метизы) испытывают нагрузку подобного вида. В конструкции корпусов, металлокаркасов, редукторов и других узлов механизмов и машин обязательно имеются соединительные детали. От их прочности зависит работоспособность устройств.

- Кручение – если на предмет действует пара сил, находящихся на определенном расстоянии друг от друга, то возникает крутящий момент. Эти усилия стремятся произвести скручивающую деформацию. Подобные нагружения наблюдаются в коробках передач, валы испытывают именно такую нагрузку. Она чаще всего непостоянная по значению. В течение времени величина действующих сил меняется.
- Изгиб – нагрузка, которая изменяет кривизну предметов, считается изгибающей. Мосты, перекладины, консоли, подъемно-транспортные механизмы и другие детали испытывают подобное нагружение.
Понятие о модуле упругости
В середине XVII века одновременно в нескольких странах начались исследования материалов. Предлагались самые разные методики по определению прочностных характеристик. Английский исследователь Роберт Гук (1660 г.) сформулировал основные положения закона по удлинению упругих тел в результате приложения нагрузки (закона Гука). Введены и понятия:
Введены и понятия:
- Напряжения σ, которое в механике измеряется в виде нагрузки, приложенной к определенной площади (кгс/см², Н/м², Па).
- Модуля упругости Е, который определяет способность твердого тела деформироваться под действием нагружения (приложения силы в заданном направлении). Единицы измерения также определяются в кгс/см² (Н/м², Па).
Формула по закону Гука записывается в виде ε = σz/E, где:
- ε – относительное удлинение;
- σz – нормальное напряжение.
Демонстрация закона Гука для упругих тел:
Из приведенной зависимости выводится значение Е для определенного материала опытным путем, Е = σz/ε.
Модуль упругости – это постоянная величина, характеризующая сопротивление тела и его конструкционного материала при нормальной растягивающей или сжимающей нагрузке.
В теории прочности принято понятие модуль упругости Юнга. Это английский исследователь дал более конкретное описание способам изменения прочностных показателей при нормальных нагружениях.
Значения модуля упругости для некоторых материалов приведены в таблице 1.
Таблица 1: Модуль упругости для металлов и сплавов
| Наименование материала | Значение модуля упругости, 10¹²·Па |
| Алюминий | 65…72 |
| Дюралюминий | 69…76 |
| Железо, содержание углерода менее 0,08 % | 165…186 |
| Латунь | 88…99 |
| Медь (Cu, 99 %) | 107…110 |
| Никель | 200…210 |
| Олово | 32…38 |
| Свинец | 14…19 |
| Серебро | 78…84 |
| Серый чугун | 110…130 |
| Сталь | 190…210 |
| Стекло | 65…72 |
| Титан | 112…120 |
| Хром | 300…310 |
Модуль упругости для разных марок стали
Металлурги разработали несколько сотен марок сталей. Им свойственны разные значения прочности. В таблице 2 показаны характеристики для наиболее распространенных сталей.
Им свойственны разные значения прочности. В таблице 2 показаны характеристики для наиболее распространенных сталей.
Таблица 2: Упругость сталей
| Наименование стали | Значение модуля упругости, 10¹²·Па |
| Сталь низкоуглеродистая | 165…180 |
| Сталь 3 | 179…189 |
| Сталь 30 | 194…205 |
| Сталь 45 | 211…223 |
| Сталь 40Х | 240…260 |
| 65Г | 235…275 |
| Х12МФ | 310…320 |
| 9ХС, ХВГ | 275…302 |
| 4Х5МФС | 305…315 |
| 3Х3М3Ф | 285…310 |
| Р6М5 | 305…320 |
| Р9 | 320…330 |
| Р18 | 325…340 |
| Р12МФ5 | 297…310 |
| У7, У8 | 302…315 |
| У9, У10 | 320…330 |
| У11 | 325…340 |
| У12, У13 | 310…315 |
Видео: закон Гука, модуль упругости.
Модули прочности
Кроме нормального нагружения, существуют и иные силовые воздействия на материалы.
Модуль сдвига G определяет жесткость. Эта характеристика показывает предельное значение нагрузки изменению формы предмета.
Модуль объемной упругости К определяет упругие свойства материала изменить объем. При любой деформации происходит изменение формы предмета.
Коэффициент Пуассона μ определяет изменения отношение величины относительного сжатия к растяжению. Эта величина зависит только от свойств материала.
Для разных сталей значения указанных модулей приведены в таблице 3.
Таблица 3: Модули прочности для сталей
| Наименование стали | Модуль упругости Юнга, 10¹²·Па | Модуль сдвига G, 10¹²·Па | Модуль объемной упругости, 10¹²·Па | Коэффициент Пуассона, 10¹²·Па |
| Сталь низкоуглеродистая | 165…180 | 87…91 | 45…49 | 154…168 |
| Сталь 3 | 179…189 | 93…102 | 49…52 | 164…172 |
| Сталь 30 | 194…205 | 105…108 | 72…77 | 182…184 |
| Сталь 45 | 211…223 | 115…130 | 76…81 | 192…197 |
| Сталь 40Х | 240…260 | 118…125 | 84…87 | 210…218 |
| 65Г | 235…275 | 112…124 | 81…85 | 208…214 |
| Х12МФ | 310…320 | 143…150 | 94…98 | 285…290 |
| 9ХС, ХВГ | 275…302 | 135…145 | 87…92 | 264…270 |
| 4Х5МФС | 305…315 | 147…160 | 96…100 | 291…295 |
| 3Х3М3Ф | 285…310 | 135…150 | 92…97 | 268…273 |
| Р6М5 | 305…320 | 147…151 | 98…102 | 294…300 |
| Р9 | 320…330 | 155…162 | 104…110 | 301…312 |
| Р18 | 325…340 | 140…149 | 105…108 | 308…318 |
| Р12МФ5 | 297…310 | 147…152 | 98…102 | 276…280 |
| У7, У8 | 302…315 | 154…160 | 100…106 | 286…294 |
| У9, У10 | 320…330 | 160…165 | 104…112 | 305…311 |
| У11 | 325…340 | 162…170 | 98…104 | 306…314 |
| У12, У13 | 310…315 | 155…160 | 99…106 | 298…304 |
Для других материалов значения прочностных характеристик указывают в специальной литературе. Однако, в некоторых случаях проводят индивидуальные исследования. Особенно актуальны подобные исследования для строительных материалов. На предприятиях, где выпускают железобетонные изделия, регулярно проводят испытания по определению предельных значений.
Модуль упругости для стали, а также для других материалов
Перед тем, как использовать какой-либо материал в строительных работах, следует ознакомиться с его физическими характеристиками для того, чтобы знать как с ним обращаться, какое механическое воздействие будет для него приемлемым, и так далее. Одной из важных характеристик, на которые очень часто обращают внимание, является модуль упругости.
Ниже рассмотрим само понятие, а также эту величину по отношению к одному из самых популярных в строительстве и ремонтных работах материалу — стали. Также будут рассмотрены эти показатели у других материалов, ради примера.
Модуль упругости — что это?
Модулем упругости какого-либо материала называют совокупность физических величин, которые характеризуют способность какого-либо твёрдого тела упруго деформироваться в условиях приложения к нему силы. Выражается она буквой Е. Так она будет упомянута во всех таблицах, которые будут идти далее в статье.
Невозможно утверждать, что существует только один способ выявления значения упругости. Различные подходы к изучению этой величины привели к тому, что существует сразу несколько разных подходов. Ниже будут приведены три основных способа расчёта показателей этой характеристики для разных материалов:
- Модуль Юнга (Е) описывает сопротивление материала любому растяжению или сжатию при упругой деформации. Определяется вариант Юнга отношением напряжения к деформации сжатия. Обычно именно его называют просто модулем упругости.
- Модуль сдвига (G), называемый также модулем жёсткости. Этот способ выявляет способность материала оказывать сопротивление любому изменению формы, но в условиях сохранения им своей нормы. Модуль сдвига выражается отношением напряжения сдвига к деформации сдвига, которая определяется в виде изменения прямого угла между имеющимися плоскостями, подвергающимися воздействию касательных напряжений. Модуль сдвига, кстати, является одной из составляющих такого явления, как вязкость.
- Модуль объёмной упругости (К), которые также именуется модулем объёмного сжатия. Данный вариант обозначает способность объекта из какого-либо материала изменять свой объём в случае воздействия на него всестороннего нормального напряжения, являющимся одинаковым по всем своим направлениям. Выражается этот вариант отношением величины объёмного напряжения к величине относительного объёмного сжатия.
- Существуют также и другие показатели упругости, которые измеряются в других величинах и выражаются другими отношениями. Другими ещё очень известными и популярными вариантами показателей упругости являются параметры Ламе или же коэффициент Пуассона.
Таблица показателей упругости материалов
Перед тем, как перейти непосредственно к этой характеристике стали, рассмотрим для начала, в качестве примера и дополнительной информации, таблицу, содержащую данные об этой величине по отношению к другим материалам.4 МПа
Значения показателей упругости стали разнятся, так как существуют сразу несколько модулей, которые исчисляются и высчитываются по-разному. Можно заметить тот факт, что в принципе сильно показатели не разнятся, ч
Модули упругости и коэффициенты Пуассона для некоторых материалов 013
|
Материал |
Модули упругости, МПа |
Коэффициент Пуассона | |
|
Модуль Юнга E |
Модуль сдвига G | ||
|
Чугун белый, серый Чугун ковкий |
(1,15…1,60)·105 1,55·105 |
4,5·104 — |
0,23…0,27 — |
|
Сталь углеродистая Сталь легированная |
(2,0…2,1)·105 (2,1…2,2)·105 |
(8,0…8,1)·104 (8,0…8,1)·104 |
0,24…0,28 0,25…0,30 |
|
Медь прокатная Медь холоднотянутая Медь литая |
1,1·105 1,3·105 0,84·105 |
4,0·104 4,9·104 — |
0,31…0,34 — — |
|
Бронза фосфористая катаная Бронза марганцовистой катаная Бронза алюминиевая литая |
1,15·105 1,1·105 1,05·105 |
4,2·104 4,0·104 4,2·104 |
0,32…0,35 0,35 — |
|
Латунь холоднотянутая Латунь корабельная катаная |
(0,91…0,99)·105 1,0·105 |
(3,5…3,7)·104 — |
0,32…0,42 0,36 |
|
Алюминий катаный Проволока алюминиевая тянутая Дюралюминий катаный |
0,69·105 0,7·105 0,71·105 |
(2,6…2,7)·104 — 2,7·104 |
0,32…0,36 — — |
|
Цинк катаный |
0,84·105 |
3,2·104 |
0,27 |
|
Свинец |
0,17·105 |
0,7·104 |
0,42 |
|
Лед |
0,1·105 |
(0,28…0,3)·104 |
— |
|
Стекло |
0,56·105 |
0,22·104 |
0,25 |
|
Гранит |
0,49·105 |
— |
— |
|
Известняк |
0,42·105 |
— |
— |
|
Мрамор |
0,56·105 |
— |
— |
|
Песчаник |
0,18·105 |
— |
— |
|
Каменная кладка из гранита Каменная кладка из известняка Каменная кладка из кирпича |
(0,09…0,1)·105 0,06·105 (0,027…0,030)·105 |
— — — |
— — — |
|
Бетон при пределе прочности, МПа: 10 15 20 |
(0,146…0,196)·105 (0,164…0,214)·105 (0,182…0,232)·105 |
— — — |
0,16…0,18 0,16…0,18 0,16…0,18 |
|
Древесина вдоль волокон Древесина поперек волокон |
(0,1…0,12)·105 (0,005…0,01)·105 |
0,055·104 — |
— — |
|
Каучук |
0,00008·105 |
— |
0,47 |
|
Текстолит |
(0,06…0,1)·105 |
— |
— |
|
Гетинакс |
(0,1…0,17)·105 |
— |
— |
|
Бакелит |
(2…3)·103 |
— |
0,36 |
|
Висхомлит (ИМ-44) |
(4,0…4,2)·103 |
— |
0,37 |
|
Целлулоид |
(1,43…2,75)·103 |
— |
0,33…0,38 |
Модуль упругости Юнга для металлов и сплавов
Эластичность материала удобно выражать с помощью отношения напряжения к деформации, параметра, также называемого модулем упругости при растяжении или модулем Юнга материала — обычно с символом — E .
- Модуль Юнга можно использовать для прогнозирования удлинения или сжатия объекта.
Модуль упругости для некоторых распространенных металлов при различных температурах в соответствии с ASME B31.1-1995:
- 1 фунт / дюйм (фунт / дюйм 2 ) = 1 фунт / дюйм (фунт / дюйм 2 ) = 144 фунт / дюйм (фунт / дюйм f / фут 2 ) = 6 894,8 Па (Н / м 2 ) = 6,895×10 -3 Н / мм 2
- T ( o C) = 5/9 [T ( o F) — 32]
Для полный стол с более высокими температурами — поворот экрана!
5 9014 9014 9015 9014 9015 9014 9014 9014 27,1 26,5
4 9015 — 9 Никелевые стали 29% Никелевые стали
C, C, C, C, C, 13,7
Сплавы из монель N04400)| Модуль упругости Юнга — E — (10 6 psi) | |||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Металл | Температура ( o C) | ||||||||||||||||||||||||||||||
| -200 | -129 | -73 | 21 | 93 | 149 | 204 | 260 | 316 | 371 | 427 | 482 | 538 | 593 | 649 | |||||||||||||||||
| Температура ( o F) | |||||||||||||||||||||||||||||||
| -325 | -200 | -100 | 70 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | 1000 | 1100 | 1200 | |||||||||||||||||
| Чугун | |||||||||||||||||||||||||||||||
| Серый чугун | 13 .4 | 13,2 | 12,9 | 12,6 | 12,2 | 11,7 | 11,0 | 10,2 | |||||||||||||||||||||||
| Сталь | Углеродистая сталь | 30,2 | 29,5 | 28,8 | 28,3 | 27,7 | 27,3 | 26,7 | 25,5 | 24,2 | 22,4 | 20.4 | 18,0 | ||||||||||||||||||
| Углеродистая сталь C => 0,3% | 31,2 | 30,6 | 30,0 | 29,3 | 28,6 | 28,1 | 27,5 | 28,1 | 27,5 | ||||||||||||||||||||||
| 22,2 | 20,2 | 17,9 | 15,4 | ||||||||||||||||||||||||||||
| Углерод-молибденовая сталь | 31,1 | 30,5 | 29,9 | 29,2 | 28.5 | 28,0 | 27,4 | 27,0 | 26,4 | 25,3 | 23,9 | 22,2 | 20,1 | 17,8 | 15,3 | 17,8 | 15,3 | ||||||||||||||
| 28,5 | 27,8 | 27,1 | 26,7 | 26,1 | 25,7 | 25,2 | 24,6 | 23,0 | |||||||||||||||||||||||
| 31 Cr / 2 стали | 6 | 31,0 | 30,4 | 29,7 | 29,0 | 28,5 | 27,9 | 27,5 | 26,9 | 26,3 | 25,5 | 24,8 | 24,8 | стали Cr 2 1/4% — 3% | 32,6 | 32,0 | 31,4 | 30,6 | 29,8 | 29,4 | 28,8 | 28,3 | 27,7 | 27.1 | 26,3 | 25,6 | 24,6 | 23,7 | 22,5 | ||
| Cr-Mo стали Cr 5% — 9% | 32,9 | 32,3 | 31,7 | 30,9 90,19 29,0 | 28,6 | 28,0 | 27,3 | 26,1 | 24,7 | 22,7 | 20,4 | 18,2 | |||||||||||||||||||
| Хромистые стали Cr 12%, 17%, 27% 31148 | 2 | 30,7 | 30,1 | 29,2 | 28,5 | 27,9 | 27,3 | 26,7 | 26,1 | 25,6 | 24,7 | 23,2 | |||||||||||||||||||
| 23,2 | |||||||||||||||||||||||||||||||
| TP304, 310, 316, 321, 347) | 30,3 | 29,7 | 29,1 | 28,3 | 27,6 | 27,0 | 26,5 | 25,8 | 25.3 | 24,8 | 24,1 | 23,5 | 22,8 | 22,1 | 21,2 | ||||||||||||||||
| Медь и медные сплавы | |||||||||||||||||||||||||||||||
| Сравн. и этилированной Sn-бронзы (C83600, C92200) | 14,8 | 14,6 | 14,4 | 14,0 | 13,7 | 13,4 | 13,2 | 12,9 | 12,5 | латунь Si & Al бронза (C46400, C65500, C95200, C95400) | 15.9 | 15,6 | 15,4 | 15,0 | 14,6 | 14,4 | 14,1 | 13,8 | 13,4 | 12,8 | |||||||||||
| 16,0 | 15,6 | 15,4 | 15,0 | 14,7 | 14,2 | ||||||||||||||||||||||||||
| Медно-красный латунь Al-14200, C10200, C10200, C10200, C10200, C10200 ) | 18.0 | 17,7 | 17,5 | 17,0 | 16,6 | 16,3 | 16,0 | 15,6 | 15,1 | 14,5 | |||||||||||||||||||||
| 27,8 | 27,3 | 26,8 | 26,0 | 25,4 | 25,0 | 24,7 | 24,3 | 24,1 | 23.7 | 23,1 | 22,6 | 22,1 | 21,7 | 21,2 | |||||||||||||||||
| Титан | |||||||||||||||||||||||||||||||
| Нелегированный титан марок 1, 2, 3 и 7 | |||||||||||||||||||||||||||||||
| 14,0 | 13,3 | 12,6 | 11,9 | 11,2 | |||||||||||||||||||||||||||
| Алюминий и алюминиевые сплавы | |||||||||||||||||||||||||||||||
| Сплавы 443, 1060, 1100, 30063, 3008 904, 601 | 10,8 | 10,5 | 10,0 | 9,6 | 9,2 | 8,7 | |||||||||||||||||||||||||
- 900b / 1 фунт / кв. 2 (Па)
- T ( o C) = 5/9 [T ( o F) — 32]
Примечание! Вы можете использовать конвертер единиц давления для переключения единиц модуля упругости.
Эластичность, упругие свойства
Объемные упругие свойства материала определяют, насколько он будет сжиматься при заданной величине внешнего давления.Отношение изменения давления к дробному объему сжатия называется объемным модулем материала.
Репрезентативная стоимость для большого количества , а для воды — . Величина, обратная модулю объемной упругости, называется сжимаемостью вещества. Величина сжатия |
Модуль объемной упругости твердого тела влияет на скорость звука и других механических волн в материале.Это также фактор количества энергии, хранящейся в твердом материале земной коры. Это накопление упругой энергии может сильно высвободиться при землетрясении, поэтому знание модулей объемной массы для материалов земной коры является важной частью изучения землетрясений. Объемный модуль упругости является фактором скорости сейсмических волн от землетрясений.
Распространено утверждение, что вода — несжимаемая жидкость. Это не совсем так, о чем свидетельствует его конечный модуль объемной упругости, но степень сжатия очень мала.На дне Тихого океана на глубине около 4000 метров давление около 4 x 10 7 Н / м 2 . Даже при таком огромном давлении относительное объемное сжатие составляет всего около 1,8%, а для стали — всего около 0,025%. Так что будет справедливо сказать, что вода почти несжимаема. Ссылка: Холлидей, Резник, Уокер, 5-е изд. Расширенный.
Джон Херманс указывает, что для более точной картины сжимаемости воды необходимо учитывать температуру.Причина, по которой сжатие 1,8% может быть указано выше, состоит в том, что сжимаемость воды при 20 ° C на поверхности примерно такая же, как сжимаемость на глубине 4000 м, если температура на дне составляет 5 ° C. Сжимаемость при таком давлении и глубине имеет более высокое значение из-за более низкой температуры, чем было бы при 20 ° C. Используя подробные данные о сжимаемости воды из компиляции Fine & Millero, можно увидеть, что если бы температура на дне составляла 5 ° C, сжатие было бы примерно 1.82%, но если бы это было 20 ° C, степень сжатия составила бы около 1,66%.
900 ° C
| Температура ° C | Давление Атм | Сжимаемость на мбар | % Сжатие при 400 бар |
| 20 ° C | 0 | 45,895 | |
| 400 | 45,498 | 1,82% | |
| 20 ° C | 400 | 41,492 | 1.66% |
Другой способ заявить, что если температура дна составляет 5 ° C, сжимаемость уменьшится только на 0,9% от поверхности к глубине, тогда как, если температура дна также будет 20 ° C, сжимаемость снизится примерно на 9,6%.
Интерес Hermance к этой подробной картине сжимаемости исходит из приложения к сжимаемости грунтовых вод в недрах Земли. Эти грунтовые воды могут иметь более высокую температуру, и изменение сжимаемости имеет большое значение для понимания процессов хранения и высвобождения грунтовых вод из трещин и пор в породе, а также последствий гидроразрыва пласта, землетрясений и т. Д., в верхней коре Земли.
Ссылка: Fine, R. A. и Millero, F. J., 1973. «Сжимаемость воды как функция температуры и давления», Journal of Chemical Physics 59 (10): 5529-5536. DOI: 10,1063 / 1,1679903.
Что такое модуль упругости? (с рисунками)
Модуль упругости, также известный как модуль упругости или модуль Юнга, является мерой того, как материал или конструкция будут деформироваться и деформироваться при воздействии напряжения. Материалы деформируются по-разному при приложении нагрузок и напряжений, и соотношение между напряжением и деформацией обычно меняется.Способность материала сопротивляться или передавать напряжение важна, и это свойство часто используется для определения того, подходит ли конкретный материал для определенной цели.
Инженеры должны понимать прочность и эластичность конструкций и материалов.
Это свойство часто определяется в лаборатории с помощью экспериментального метода, известного как испытание на растяжение , которое обычно проводится на образце материала определенной формы и размеров.Доступны различные испытательные устройства, которые прикладывают очень точные нагрузки и напряжения к образцу, а также точно измеряют и записывают любую результирующую деформацию в материале. Модуль упругости известен для самых разных конструкционных материалов, включая металлы, дерево, стекло, резину, керамику, бетон и пластмассы.
Типовое измерение, модуль упругости может использоваться для определения того, сколько бетона может выдержать напряжение, затвердевшее до разрушения или деформации.
Модуль упругости описывает соотношение между напряжением, приложенным к материалу, и его соответствующей деформацией. Напряжение определяется как сила, приложенная к единице площади, с типичными единицами измерения фунтов на квадратный дюйм (фунт / кв. Дюйм) или ньютонов на квадратный метр, также известных как паскалях (Па). Деформация — это мера степени деформации материала при приложении напряжения, которая рассчитывается путем измерения степени деформации под напряжением по сравнению с исходными размерами материала.Модуль упругости основан на законе упругости Гука и может быть рассчитан путем деления напряжения на деформацию.
Для многих материалов при низких уровнях напряжения и при растяжении напряжение и деформация пропорциональны — это означает, что они постоянно увеличиваются и уменьшаются относительно друг друга.Деформация материала, возникающая при пропорциональном поведении напряжения и деформации, известна как упругая деформация или упругая деформация . Модуль упругости описывает взаимосвязь между напряжением и деформацией в этих условиях.
Эластичность — это способность материала возвращаться в исходное состояние или размеры после снятия нагрузки или напряжения.Упругая деформация обратима, то есть деформация исчезнет после снятия напряжения и материал вернется в исходное состояние. Материалы, которые подвергаются интенсивным уровням напряжения, могут деформироваться до такой степени, что напряжение и деформация больше не будут вести себя пропорционально, и материал не вернется к своим первоначальным размерам. Это называется пластической деформацией или пластической деформацией .
МЕХАНИЧЕСКИЕ СВОЙСТВА МЕТАЛЛОВ И СПЛАВОВ
Механические свойства имеют первостепенное значение в более крупных промышленных применениях металлов, поэтому они требуют большого внимания при их изучении.
Прочность. — Прочность материала — это свойство сопротивления внешним нагрузкам или напряжениям без повреждения конструкции. Термин «предел прочности » относится к удельному напряжению (фунты на квадратный дюйм), развиваемому в материале в результате максимальной медленно прикладываемой нагрузки, которой материал может выдержать без разрыва при испытании на растяжение. Испытание на растяжение наиболее часто применяется к металлам, потому что оно говорит об их свойствах гораздо больше, чем любое другое отдельное испытание.В металлургии о разрушении часто говорят как об отказе, разрыве или разрушении; перелом металла — это название, данное поверхности, на которой произошел перелом.
Прочность металлов и сплавов зависит от двух факторов, а именно, прочности кристаллов, из которых они состоят, и прочности сцепления между этими кристаллами. Самое сильное известное вещество — это вольфрамовая проволока электрических ламп накаливания. Чистое железо непрочно, но когда сталь легируется углеродом для получения стали, она может быть прочнее любого из чистых металлов, кроме вольфрама.
Напряжение и деформация. — Напряжение — это сила внутри тела, которая сопротивляется деформации из-за приложенной извне нагрузки. Если эта нагрузка действует на поверхность единичной площади, она называется единичной силой, а сопротивление ей — единиц. Таким образом, количественно напряжение — это сила на единицу площади; на европейском континенте он выражается в килограммах на квадратный миллиметр, в Соединенных Штатах — фунтах на квадратный дюйм, а в Англии обычно используются длинные тонны на квадратный дюйм.
Когда внешняя сила действует на эластичный материал, материал деформируется, и деформация пропорциональна нагрузке. Это искажение или деформация составляет деформаций, единиц деформации, которая измеряется в Соединенных Штатах и в Англии в дюймах на дюйм, в то время как в Европе она измеряется в сантиметрах на сантиметр. Единичная деформация — это отношение расстояний или длин.
Эластичность. — Любой материал, подверженный внешней нагрузке, деформирован или деформирован.Упруго напряженные материалы возвращаются к своим первоначальным размерам при снятии нагрузки, если она не слишком велика. Такое искажение или деформация пропорциональна величине нагрузки до определенной точки, но когда нагрузка слишком велика, материал постоянно деформируется, а при дальнейшем увеличении нагрузки до определенной точки материал разрушается. Свойство восстановления исходных размеров после снятия внешней нагрузки известно как эластичность .
Модуль упругости. — В пределах упругости отношение напряжения к деформации известно как модуль упругости (то есть мера упругости).
Модуль упругости выражает жесткость материала. Для стали и большинства металлов это постоянное свойство, на которое мало влияет термическая обработка, горячая или холодная обработка или фактический предел прочности металла. Их модули упругости показывают, что, когда стержни из стали и алюминия одинакового размера подвергаются одинаковой нагрузке, возникающая в результате упругая деформация в алюминии будет почти в три раза больше, чем в стальном стержне.
Пропорциональный предел упругости. — Металлы обычно не эластичны во всем диапазоне нагрузок. Предел пропорциональности напряжения к деформации известен как предел пропорциональности . Предел упругости — это максимальное удельное напряжение, которое испытываемый образец будет выдерживать и все еще возвращаться к своим исходным размерам после снятия нагрузки. Предел пропорциональности и предел упругости в металлах очень близки друг к другу, настолько, что их часто путают, и теперь принято объединять их в один термин «Предел пропорциональности». Это важное свойство, напряжение, которое нельзя превышать при проектировании.
Природа эластичности. — Эластичность металлического вещества является функцией сопротивления его атомов разделению, сжатию или вращению друг относительно друга и, таким образом, является фундаментальным свойством материала. Итак, эластичность демонстрируется как функция атомных сил. Это объясняет, почему модуль упругости прочной и хрупкой термообработанной легированной стали точно такой же, как у сравнительно слабой и вязкой отожженной стали.
Предел текучести. — Это точка на кривой «напряжение-деформация», в которой напряжение выравнивается или фактически уменьшается, а напряжение продолжается. Этот термин строго применим только к малоуглеродистым сталям, поскольку определяющая его характеристика не встречается в других металлах, легированных сталях или даже холоднодеформированных или нормализованных низкоуглеродистых сталях.
Максимальная сила. — Наибольшая нагрузка, которую выдерживает образец, деленная на первоначальную площадь поперечного сечения, называется пределом прочности на разрыв или пределом прочности детали.
Пластичность. — Пластичность — это способность металла постоянно деформироваться при растяжении без разрушения. В частности, этот термин обозначает емкость, которую нужно тянуть от проволоки большего диаметра к меньшему. Такая операция, очевидно, включает в себя как удлинение, так и уменьшение площади, и значения этих двух характеристик металла, определенные при испытании на растяжение, обычно принимаются в качестве меры пластичности металла.
Прочность. — Вязкость определяется как свойство поглощения значительной энергии до разрушения. Это мера общей способности материала поглощать энергию, включая энергию как упругой, так и пластической деформации при постепенно прикладываемой нагрузке. Одним из наиболее распространенных тестов на ударную вязкость является «испытание на удар», в котором измеряется энергия, поглощенная при разрушении образца внезапным ударом.
Природа прочности. — Прочность металла определяется степенью скольжения, которая может происходить внутри кристаллов, не приводя к разрыву металла.Возможно, это результат попеременного проскальзывания и расклинивания каждой клиновидной кристаллографической плоскости, удерживаемой до приложения большего напряжения. Хрупкий металл или сплав либо не перестанет скользить после достижения упругой деформации, либо остановится только на короткое время перед разрушением. Очевидно, что последовательная остановка и проскальзывание вызовут деформацию; поэтому вязкие металлы и сплавы часто являются наиболее пластичными и пластичными.
Иногда кристаллы металла могут быть прочными, но границы кристаллов могут содержать примеси, так что наименьшая деформация кристаллической массы может вызвать растрескивание через хрупкий материал границ зерен.Это верно для стали, содержащей значительное количество фосфора, и для меди, содержащей висмут.
Ковкость. — Ковкость — это свойство металла, которое допускает остаточную деформацию при сжатии без разрушения. В частности, это означает способность раскатывать или забивать тонкие листы. Свойство пластичности похоже, но не то же самое, что и пластичность, и разные металлы не обладают этими двумя свойствами в одинаковой степени: хотя свинец и олово относительно высоки в порядке пластичности, им не хватает необходимой прочности на разрыв. быть втянутым в тонкую проволоку.Большинство металлов обладают повышенной ковкостью и пластичностью при более высоких температурах. Например, железо и никель очень пластичны при ярко-красном огне (1000 ° C).
Хрупкость. — Хрупкость подразумевает внезапный отказ. Это свойство ломаться без предупреждения, то есть без видимой остаточной деформации. Это противоположность ударной вязкости в том смысле, что хрупкое тело имеет небольшое сопротивление разрыву после достижения предела упругости. Хрупкость противоположна пластичности в том смысле, что она предполагает разрыв без значительной деформации.Часто твердые металлы хрупкие, но эти термины не следует путать или использовать как синонимы.
Усталостный отказ. — Если металл подвергается частым повторяющимся нагрузкам, он в конечном итоге сломается и выйдет из строя.
Чередование стресса приведет к неудаче быстрее, чем повторение стресса. Под «чередованием напряжений» подразумевается попеременное растяжение и сжатие в любом волокне. Разрушение металлов и сплавов под действием повторяющихся или переменных нагрузок, слишком малых, чтобы вызвать даже остаточную деформацию при статическом применении, называется усталостным разрушением .
Коррозионная усталость. — Если элемент подвергается также воздействию коррозионных агентов, таких как влажная атмосфера или масло, не очищенное от кислоты, нагрузка, необходимая для выхода из строя, намного ниже. Самые прочные стали не выдерживают усталости и коррозии при удельном напряжении волокна не более 24000 фунтов на квадратный дюйм, даже если их предел прочности может указывать на то, что они могут выдерживать гораздо более высокое напряжение. Интересно отметить, что удельное напряжение чрезвычайно прочной термически обработанной легированной стали, подверженной коррозионной усталости, будет не больше, чем у относительно слабой конструкционной стали.Очевидна важность защиты поверхностей усталостных элементов от коррозии с помощью цинкования, гальванизации и т. Д., Если и когда это возможно.
Твердость. — Качество твердости является комплексным, и подробное исследование показало, что это сочетание ряда физических и механических свойств. Его чаще определяют в терминах метода, используемого для его измерения, и обычно означает сопротивление вещества вдавливанию. Твердость также может быть определена с точки зрения устойчивости к царапинам и, таким образом, связана с износостойкостью.Термин твердость иногда используется для обозначения жесткости или состояния деформируемых изделий, поскольку твердость металла при вдавливании тесно связана с его пределом прочности при растяжении.
В инженерной практике сопротивление металла проникновению твердого инструмента для вдавливания обычно принимается как определяющее свойство твердости. Был разработан ряд стандартизированных испытательных машин и пенетраторов, наиболее распространенными из которых являются машины Бринелля, Роквелла и Виккерса.
В испытании Бринелля шарик из закаленной стали диаметром 10 мм вдавливается в поверхность испытываемого материала под нагрузкой 500 или 3000 кг и измеряется площадь вдавливания.Затем твердость по Бринеллю выражается как отношение приложенной нагрузки к площади слепка.
В тестах Rockwell используется ряд различных масштабов тестирования с использованием различных пенетраторов и нагрузок. Наиболее часто используемые шкалы — это шкала «C», в которой используется алмазный конусный пенетратор при основной нагрузке 150 кг, и шкала «B», в которой используется закаленный стальной шар диаметром 1/16 дюйма при основной нагрузке 100 кг. кг. В этом испытании в качестве меры твердости принимается разница глубины проникновения между глубиной проникновения малой нагрузки в 10 кг и приложенной основной нагрузкой.
В тесте Виккерса используется квадратный индентор в виде ромбовидной пирамиды, который может быть нагружен от 1 до 120 кг. Как и в тесте Бринелля, твердость выражается через приложенную нагрузку, деленную на площадь поверхности пирамидального отпечатка.
Тест Бринелля обычно используется только для довольно толстых срезов, таких как прутки и поковки, в то время как тест Роквелла обычно используется как для толстых, так и для тонких срезов, таких как полосы и трубки. Поверхностный Роквелл можно использовать для деталей толщиной до 0.010 дюймов. Тестер Виккерса чаще всего используется как лабораторный прибор для очень точных измерений твердости, а не как инструмент производственного контроля.
Склероскоп Шора измеряет упругость, а не твердость, хотя они взаимосвязаны. Склероскоп измеряет отскок падающего молотка от испытательной поверхности, и число твердости выражается как высота отскока в терминах максимального отскока от полностью закаленной высокоуглеродистой стали.
Природа твердости и мягкости. — Сопротивление металла проникновению другим телом, очевидно, частично зависит от силы сопротивления его межатомных связей. На это указывает почти точная параллель порядка твердости металлов и их модулей упругости.