Объемы формулы: Формулы объема геометрических фигур
- Формулы объема и программы для расчета объема
- Формулы объема геометрических фигур.
- Как найти Объем Параллелепипеда?
- Формулы площадей и объемов геометрических фигур
- Формулы площадей
- Формулы объемов
- Площадь многоугольника
- Площадь треугольника
- Площадь квадрата
- Площадь прямоугольника
- Площадь параллелограмма
- Площадь ромба
- Площадь трапеции
- Площадь четырехугольника
- Площадь круга
- Площадь кругового сектора, длина дуги
- Площадь эллипса
- Объем куба
- Объем параллелепипеда
- Объем призмы
- Объем пирамиды
- Объем усеченной пирамиды
- Объем цилиндра
- Объем правильной треугольной пирамиды
- Объем конуса
- Объем усеченного конуса
- Объем тетраэдра
- Объем шара
- Объем шарового сегмента и сектора
- 4.
- Достаточно знать всего одну формулу, чтобы вычислять и площади, и объемы различных фигур (Формула Симпсона) | Строю для себя
- Урок 11. понятие объема — Геометрия — 11 класс
- Периметр, площадь и объем
- Формулы объема
- Объемные формулы – вывод, примеры
- Объем — определение, формула, калькулятор, примеры
- Часто задаваемые вопросы о искусственном вскармливании: сколько и как часто (для родителей)
- Исчисление I — Формулы площади и объема
- Произошла ошибка при настройке пользовательского файла cookie
Формулы объема и программы для расчета объема
Содержание:
Объём геометрической фигуры — количественная характеристика пространства, занимаемого телом или веществом.
В простейших случаях объём измеряется числом умещающихся в теле единичных кубов, т. е. кубов с ребром, равным единице длины.
Объём тела или вместимость сосуда определяется его формой и линейными размерами.
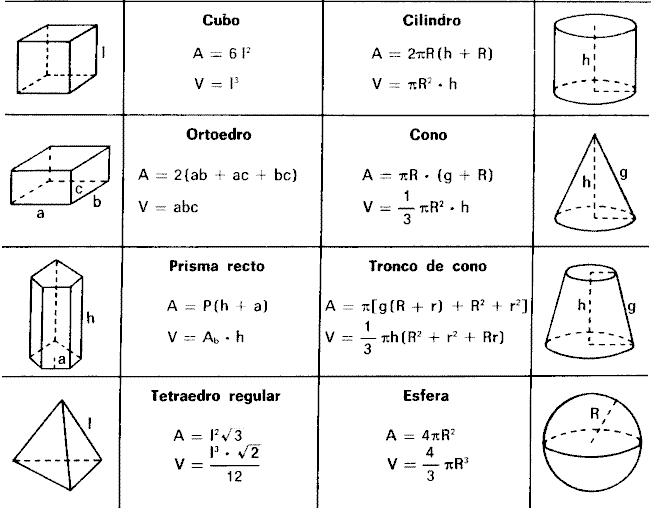
Формула объема куба
1) Объем куба равен кубу его ребра.
V — объем куба
H — высота ребра куба
См. также: Программа для расчета объема куба.
Формула объема пирамиды
1) Объем пирамиды равен одной трети произведения площади основания S (ABCD) на высоту h (OS).
V — объем пирамиды
S — площадь основания пирамиды
h — высота пирамиды
См. также: Программа для расчета объема пирамиды.
Формулы объема конуса
1) Объем конуса равен одной трети произведения площади основания на высоту.
2) Объем конуса равен одной трети произведения числа пи (3.1415) на квадрат радиуса основания на высоту.
V — объем конуса
S — площадь основания конуса
h — высота конуса
π — число пи (3.1415)
r — радиус конуса
См. также: Программа для расчета объема конуса.
Формулы объема цилиндра
1) Объем цилиндра равен произведению площади основания на высоту.
2) Объем цилиндра равен произведению числа пи (3.1415) на квадрат радиуса основания на высоту.
V — объем цилиндра
S — площадь основания цилиндра
h — высота цилиндра
π — число пи (3.1415)
r — радиус цилиндра
См. также: Программа для расчета объема цилиндра.
также: Программа для расчета объема цилиндра.
Формула объема шара
1) Объем шара вычисляется по приведенной ниже формуле.
V — объем шара
π — число пи (3.1415)
R — радиус шара
См. также: Программа для расчета объема шара.
Формула объема тетраэдра
1) Объем тетраэдра равен дроби в числителе которой корень квадратный из двух помноженный
на куб длины ребра тетраэдра, а в знаменателе двенадцать.
V — объем тетраэдра
a — длина ребра тетраэдра
См. также: Программа для расчета объема тетраэдра.
Мы помогли уже 4 372 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Формулы объема геометрических фигур.
Объем геометрической фигуры
— количественная характеристика пространства, занимаемого телом или веществом. Объём тела или вместимость сосуда определяется его формой и линейными размерами.
Объём тела или вместимость сосуда определяется его формой и линейными размерами.
Объем куба
Объем куба равен кубу длины его грани.
Формула объема куба:
V = a3
где V — объем куба,
a — длина грани куба.
Объем призмы
Объем призмы равен произведению площади основания призмы, на высоту.
Формула объема призмы:
V = So h
где V — объем призмы,
So — площадь основания призмы,
h — высота призмы.
Объем параллелепипеда
Объем параллелепипеда равен произведению площади основания на высоту.
Формула объема параллелепипеда:
V = So · h
где V — объем параллелепипеда,
So — площадь основания,
h — длина высоты.
Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
Формула объема прямоугольного параллелепипеда:
V = a · b · h
где V — объем прямоугольного параллелепипеда,
a — длина,
b — ширина,
h — высота.
Объем пирамиды
Объем пирамиды равен трети от произведения площади ее основания на высоту.
Формула объема пирамиды:
где V — объем пирамиды,
So — площадь основания пирамиды,
h — длина высоты пирамиды.
Объем правильного тетраэдра
Формула объема правильного тетраэдра:
где V — объем правильного тетраэдра,
a — длина ребра правильного тетраэдра.
Объем цилиндра
Объем цилиндра равен произведению площади его основания на высоту.
Формулы объема цилиндра:
где V — объем цилиндра,
So — площадь основания цилиндра,
R — радиус цилиндра,
h — высота цилиндра,
π = 3.141592.
Объем конуса
Объем конуса равен трети от произведению площади его основания на высоту.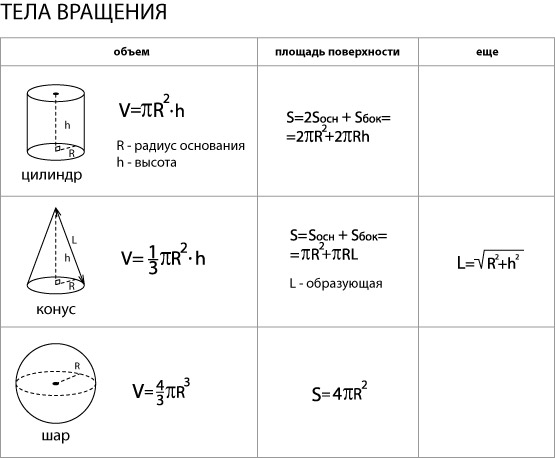
Формулы объема конуса:
где V — объем конуса,
So — площадь основания конуса,
R — радиус основания конуса,
h — высота конуса,
π = 3.141592.
Объем шара
Объем шара равен четырем третьим от его радиуса в кубе помноженного на число пи.
Формула объема шара:
где V — объем шара,
R — радиус шара,
π = 3.141592.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Как найти Объем Параллелепипеда?
Понятие объема
Чтобы без труда вычислить объём любой фигуры, нужно разобраться с определениями.
Объём — это количественная характеристика пространства, занимаемого телом или веществом.
Другими словами, это то, сколько места занимает предмет.
Объём измеряется в единицах измерения размера пространства, занимаемого телом, то есть в кубических метрах, кубических сантиметрах, кубических миллиметрах.
За единицу измерения объёма можно принять куб с ребром 1 см, то есть, кубический сантиметр (см3), кубический миллиметр (1 мм3), кубический метр (1 м3).
Объём всегда выражается в положительных числах. Это число показывает, какое именно количество единиц измерения есть в теле. Например, сколько воды в бассейне, сока в графине, земли в клумбе.
Два свойства объёма
|
Любое объемное тело имеет объем. Получается, при желании мы можем вычислить объем кружки, смартфона, вазы, кота — чего угодно.
Объем прямоугольного параллелепипеда
Параллелепипед — это многогранник с шестью гранями, каждая из которых является параллелограммом.
Прямоугольным параллелепипедом называют параллелепипед, у которого все грани являются прямоугольниками.
Формула объема прямоугольного параллелепипеда Чтобы вычислить объем прямоугольного параллелепипеда, найдите произведение его длины, ширины и высоты: V = a × b × h |
Чтобы не запутаться в формулах, запоминайте табличку с условными обозначениями.
a | длина параллелепипеда |
b | ширина параллелепипеда |
h | высота параллелепипеда |
P (осн) | периметр основания |
S (осн) | площадь основания |
S (бок) | площадь боковой поверхности |
S (п. | площадь полной поверхности |
V | объем |
Пример 1. Чему равен объем параллелепипеда со сторонами 9 см, 6 см, 3 см.
a = 9 см
b = 6 см
h = 3 см
V = a × b × h
V = 9 × 6 × 3 = 162 см3.
Ответ: объем прямоугольного параллелепипеда равен 162 см3.
Следствие Объем параллелепипеда равен произведению площади основания на высоту. V = Sосн × h |
Из этого следствия выведем формулу нахождения площади основания параллелепипеда.
Sосн = V : h
Пример 2. Найдите площадь основания параллелепипеда, если его объем равен 96 см3, а высота 8 см.
V = 96 см3
h = 8 см
V = Sосн × h
Sосн = V : h
Sосн = 82 см3 : 8 см = 12 см2.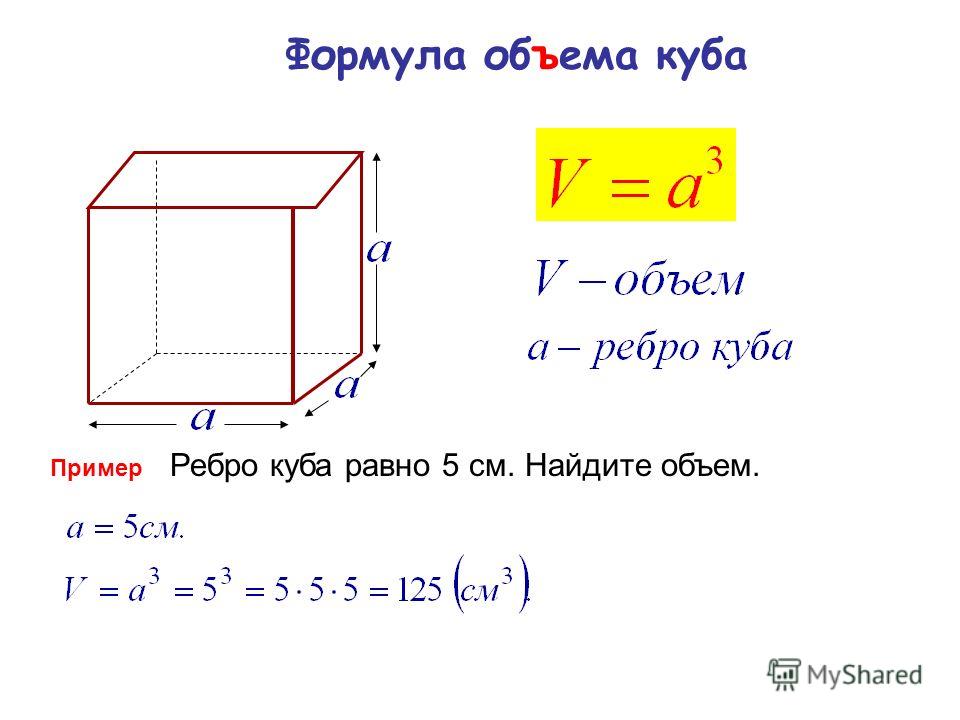
Ответ: площадь основания параллелепипеда равна 12 см2.
Обучение на курсах по математике в онлайн-школе Skysmart поможет быстрее разобраться в теме и правильно решать задачки!
Вычисление площади
Как вы уже поняли, вычисление объёма параллелепипеда напрямую зависит от вычисления его площади. Давайте разберемся, сколько всего площадей можно найти в параллелепипеде.
Чтобы найти площадь боковой поверхности параллелепипеда, вычислите по отдельности площадь каждой боковой грани, а затем найдите сумму получившихся значений.
Так как противолежащие грани прямоугольного параллелепипеда одинаковые, то получим формулу:
Чтобы вычислить площадь полной поверхности параллелепипеда, сложите площадь боковой поверхности и две площади основания. Так как площади оснований у прямоугольного параллелепипеда одинаковые, то получим формулу:
- Sп. п. = 2 (ab + ac + bc)
Пример 3. Найдем площадь поверхности параллелепипеда, если длина основания равна 6 сантиметров, ширина — 4 см соответственно, а высота — 3 см.
Sп. п. = 2 (ab + ac + bc)
Sп. п. = 2 (6 × 4 + 6 × 3 + 4 × 3) = 2 × (24 + 18 + 12) = 2 × 54 = 108 см2.
Ответ: площадь поверхности параллелепипеда — 108 см2.
Как видите, вычислить объём и найти площадь параллелепипеда совсем не трудно.
Задачи на самопроверку
Пользоваться онлайн-калькуляторами можно, когда вы уже натренировались в решении задачек и с закрытыми глазами можете вычислить объем любого параллелепипеда. Давайте разберем еще несколько примеров.
Задачка 1. Найдите объём параллелепипеда со сторонами 18 см, 10 см, 7 см.
Как решаем:
a = 18 см
b = 10 см
h = 7 см
Формула нахождения объема параллелепипеда:
V = a × b × h
Подставляем наши числа:
V = 18 × 10 × 7 = 1260 см3.
Ответ: объём параллелепипеда равен 1260 см3.
Задачка 2. Найдите площадь основания параллелепипеда, если его объём равен 120 см3, а высота — 15 см.
Как решаем:
V = 120 см
h = 15 см
V = Sосн × h
Sосн = V : h
Sосн = 120 см3: 15 см = 8 см2.
Ответ: площадь основания параллелепипеда равна 8 см2.
Задачка 3. Найдите площадь полной поверхности прямоугольного параллелепипеда, если длина основания равна 30 сантиметров, ширина равна 12 см, а высота равна 5 см.
Как решаем:
Sп. п. = 2 (ab + ac + bc)
Sп. п. = 2 (30 × 12 + 30 × 5 + 12 × 5) = 2 × (360 + 150 + 60) = 2 × 570 = 1140 см2.
Ответ: площадь полной поверхности параллелепипеда равна 1140 см2.
Пусть все необходимые формулы будут под рукой в нужный момент. Сохраняйте табличку-шпаргалку на гаджет или распечатайте ее и храните в учебнике.
V параллелепипеда | V = a × b × h |
| V = Sосн × h |
S боковой поверхности | Sб. |
S полной поверхности | Sп. п. = 2 (ab + ac + bc) |
Формулы площадей и объемов геометрических фигур
Формулы площадей
1.Площадь многоугольника.
Формулы объемов 1.Объем куба.
| ||||
|
1 2 3 4 5 6 7 8 | ||||
Площадь многоугольника | ||||
Рассчитать площадь многоугольника вписанного в круг и описанного около круга
Радиус r
| ||||
Площадь треугольника | ||||
Рассчитать площадь треугольника
| ||||
|
Сторона а Сторона b Угол ɣ (0-90°) ° S = | ||||
Площадь квадрата | ||||
Рассчитать площадь квадрата
| ||||
Площадь прямоугольника | ||||
Рассчитать площадь прямоугольника
| ||||
Площадь параллелограмма | ||||
Рассчитать площадь параллелограмма
| ||||
Площадь ромба | ||||
Рассчитать площадь ромба
| ||||
Площадь трапеции | ||||
Рассчитать площадь трапеции
| ||||
Площадь четырехугольника | ||||
Рассчитать площадь четырехугольника
| ||||
Площадь круга | ||||
Рассчитать площадь круга, длину окружности
| ||||
Площадь кругового сектора, длина дуги | ||||
Рассчитать площадь кругового сектора, длину дуги
| ||||
Площадь эллипса | ||||
Рассчитать площадь эллипса
| ||||
| ||||
Объем куба | ||||
Рассчитать объем и площадь поверхности куба
| ||||
Объем параллелепипеда | ||||
Рассчитать объем параллелепипеда
| ||||
Объем призмы | ||||
Рассчитать объем призмы
| ||||
Объем пирамиды | ||||
Рассчитать объем пирамиды
| ||||
Объем усеченной пирамиды | ||||
Рассчитать объем усеченной пирамиды
| ||||
Объем цилиндра | ||||
Рассчитать объем цилиндра
| ||||
Объем правильной треугольной пирамиды | ||||
Рассчитать объем правильной треугольной пирамиды
| ||||
Объем конуса | ||||
Рассчитать объем конуса
| ||||
Объем усеченного конуса | ||||
Рассчитать объем усеченного конуса
| ||||
Объем тетраэдра | ||||
Рассчитать объем тетраэдра
| ||||
Объем шара | ||||
Рассчитать объем и площадь поверхности шара
| ||||
Объем шарового сегмента и сектора | ||||
Рассчитать объем шарового сегмента
| ||||
|
1 2 3 4 5 6 7 8 | ||||
4.
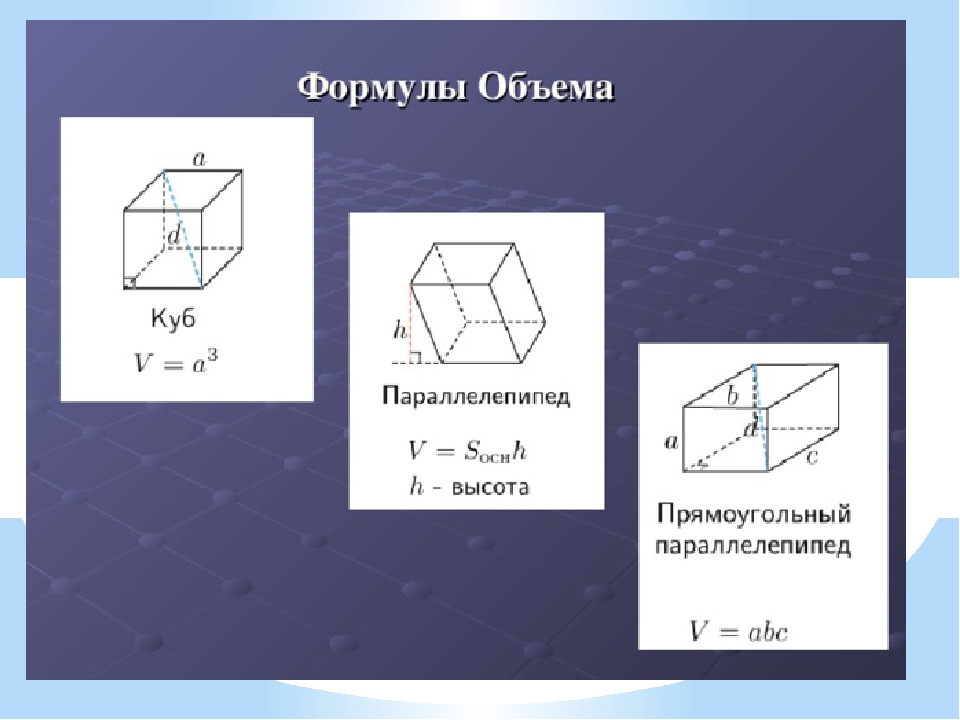 Объем фигур — Фигуры В Пространстве
Объем фигур — Фигуры В Пространстве
|
Достаточно знать всего одну формулу, чтобы вычислять и площади, и объемы различных фигур (Формула Симпсона) | Строю для себя
Приветствую Вас, уважаемые гости и подписчики моего канала!
Сегодня, хотел бы свою статью посвятить царице наук, а именно — математике! Являясь отцом двоих детей, я постоянно помогаю им с домашкой (домашними работами), в том числе и с математикой.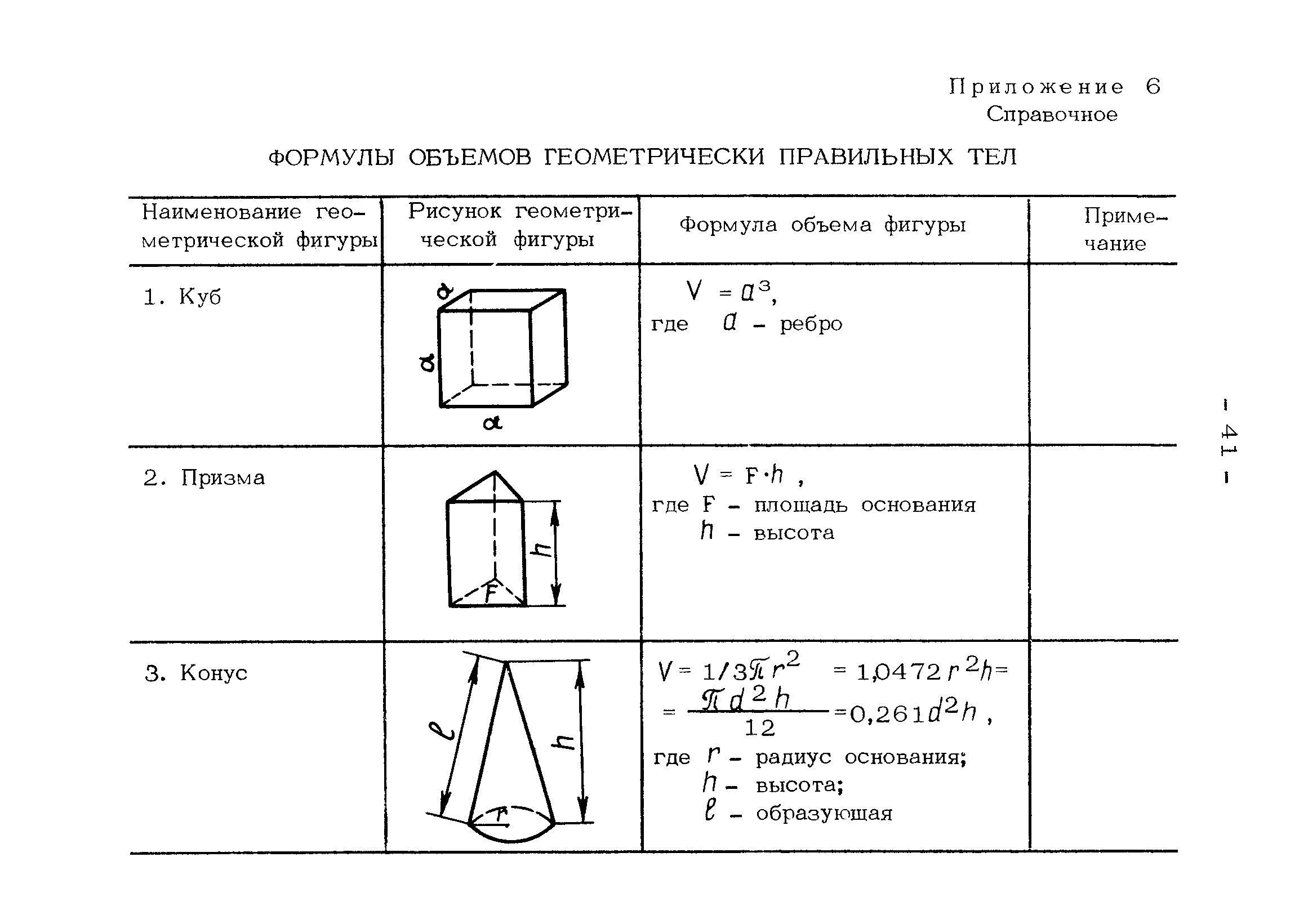 Дочери в школе задали на лето около сотни задач, и, проверяя очередную, наткнулся в учебнике на интересный параграф, который называется в честь двух великих математиков: Формула Ньютона-Симпсона.
Дочери в школе задали на лето около сотни задач, и, проверяя очередную, наткнулся в учебнике на интересный параграф, который называется в честь двух великих математиков: Формула Ньютона-Симпсона.
На самом же деле, она относится к высшей математике, а именно к приемам численного интегрирования, но благодаря своей простоте, проходят ее и в школьном курсе. С помощью одной единственной универсальной формулы Ньютона-Симпсона можно вычислять как площади фигур, так и объемы различных тел.
Формула выглядит следующим образом:
Если вычисляются объемы тел, то в качестве «b» берутся площади оснований и сечений, если же вычисляются площади, то «b» это длины оснований и отрезка по центру.
b1 — это длина или площадь нижнего основания;
b2 — это длина отрезка посередине фигуры или площадь сечения по центру тела;
b3 — это длина или площадь верхнего основания;
Проще на примерах.
 ..
..
1. Объемы
Итак, предположим нам требуется вычислить объем конуса или пирамиды. Геометрия нам говорит, что объем этих фигур равен:
V = (S*h)/3, где S — площадь основания, h — высота.
По формуле Ньютона-Симпсона это представляется так:
V=(Н/6)*(b1 + 4b2 + b3) или (Н/6)*(b1 + 4*(b1/4) + 0) = Н*b1/3.
Как вы видите формула Симпсона, путем преобразования, превращается в стандартную формулу, изучаемую в школе. Все то же самое можно проделать с цилиндром, призмой или шаром, а также с усеченными вариантами пирамиды и конуса.
В случаях с цилиндром и призмой, по формуле Ньютона-Симпсона у вас будет выведена формула объема, равная произведению высоты на основание b1, а в случае с шаром, получится реальная формула нахождения объема сферы: 4/3 *π*r³.
Уже за счет того, что формула применима для нахождения объемов самых известных геометрических фигур, она достойна называться универсальной. Кроме объема, как я уже ранее писал, с помощью нее можно вычислять и площади.
Кроме объема, как я уже ранее писал, с помощью нее можно вычислять и площади.
2. Площади
Итак…
Площадь любой произвольной трапеции:
S = h/6 * (b1 + 4(b1+b3)/2 + b3) = h/2 * (b1+b3)
Площадь треугольника:
S = h/6 * (b1 + 4(b1/2) + 0) = 1/2 *b*h
Площадь параллелограмма или правильного четырехугольника:
S = h/6 * (b1 + 4b1 + b1) = b*h
Что и требовалось доказать!
Формула очень проста и интересна, если Ваши детки не проходили ее в школе, считаю, что стоит им рассказать и показать.
А на этом всё, с Вами был Роман, канал «Строю для Себя»…
Всего доброго!
Урок 11. понятие объема — Геометрия — 11 класс
Геометрия, 11 класс
Урок №11
Понятие объёма
Перечень вопросов, рассматриваемых на уроке:
Понятие объёма.
Свойства объёмов.
Объём прямоугольного параллелепипеда.
Формула объёма прямоугольного параллелепипеда.
Тезаурус
Объём тела– величина, характеризующая часть пространства, занимаемую телом, и определяемая формой и линейными размерами этого тела.
Основные свойства объёма:
— равные тела имеют равные объёмы;
— если тело составлено из нескольких тел, то его объём равен сумме объёмов этих тел.
Основная литература:
Атанасян Л. С. и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10–11 классы [текст]: учеб. для общеобразоват. организаций: базовый и углубл. уровни – М.: Просвещение, 2014. – 255 с. С. 130–133.
Теоретический материал для самостоятельного изучения
С понятием объёмного тела, отличающегося от плоской фигуры, мы познакомились ещё в начальной школе.
Объёмом принято называть положительную величину, характеризующую часть пространства, занимаемую телом, и определяемую формой и линейными размерами этого тела.
Мы можем вычислить объём тела точно так же, как ранее находили площадь фигуры. Объём принято измерять в единицах измерения объёма (единицах измерения размера пространства, занимаемого телом), то есть в кубических метрах, сантиметрах, миллиметрах и так далее. За единицу измерения объёма можно принять куб с ребром 1 см, то есть, кубический сантиметр (обозначение: см3). По аналогии, можно за единицу измерения объёма принять кубический миллиметр (1 мм3), кубический метр (1 м3) и тому подобное.
Объём выражается в положительных числах. Это число показывает, сколько единиц измерения содержится в теле. Например, сколько кубических миллиметров в аквариуме, сколько кубических метровв бассейне и так далее.
Объём обозначается заглавной латинской буквой V.
Пример:
Объём книги400 кубических сантиметров запишут: V = 400см3.
Рассмотрим свойства объёмов.
Свойство № 1. Равные тела имеют равные объёмы. Это означает, что если два тела идентичны, то есть имеют равное количество единиц измерения и частей, то равны и их объёмы. Например, 2 одинаковых пакета молока равны в объёме.
Это означает, что если два тела идентичны, то есть имеют равное количество единиц измерения и частей, то равны и их объёмы. Например, 2 одинаковых пакета молока равны в объёме.
Свойство № 2. Если тело составлено из нескольких тел, то его объём равен сумме объёмов этих тел.
Следствие из основных свойств объёмов.
Объём куба с ребром 1/n равен 1/n3
Доказательство. Рассмотрим куб, объём которого принят за единицу измерения объёмов, тоесть равный некоторому числукубических сантиметров. Его ребро равно единице измерения отрезков. Разобьём каждое ребро этого куба на произвольное количество частей – nтак, чтобы провести плоскости, перпендикулярные к этому ребру.
По второму свойству объёмов, сумма объёмов всех кубиков равна объёму всего куба (1 см3). Следовательно, поскольку мы разбили каждое ребро на n частей, то каждый маленький куб внутри большого куба будет иметь ребро
Объём каждого из маленьких кубиков при этом будет равен 1/n3.
Объём прямоугольного параллелепипеда
Теорема
Объём прямоугольного параллелепипеда равен произведению трёх его измерений.
Доказательство
Обозначимизмеренияпрямоугольного параллелепипеда P буквами a,b,c, его объём буквой V, и докажем, что V = a ∙ b ∙ c.
Рассмотрим два возможных случая.
Случай первый. Измерения a, b и c представляют собой конечные десятичные дроби, у которых число знаков после запятой не превосходит n (можно считать, что n больше или равно 1). В этом случае числа a ∙10n, b∙10n, c∙10n, являются целыми. Разобьём каждое ребро параллелепипеда на равные части длины: 1/10n и через точки разбиения проведём плоскости, перпендикулярные к этому ребру. Параллелепипед P разобьётся на abc∙103n равных кубов с ребром 1/10n. Так как объём каждого куба равен 1/103n, что мы доказали ранее, то объём всего параллелепипеда P = abc, что и требовалось доказать.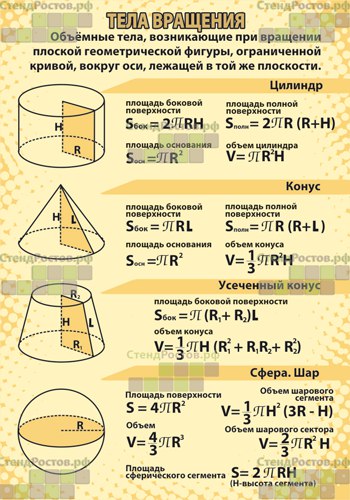
Случай второй.
Хотя бы одно из измерений a, b, c представляет собой бесконечную десятичную дробь. Рассмотрим конечные десятичные дроби: an, bn, cn, которые получаются из чисел a, b, c, если отбросить в каждом из них все цифры после запятой, начиная с n + 1. Очевидно, an ≤ a ≤ an’, где an’ = an+1 : 10n. Аналогичные неравенства справедливы для b и c. Перемножив эти неравенства, получим произведение anbncn ≤ abc ≤ an’bn’cn’, где bn’= bn+1 : 10n, cn’ = cn+1 : 10n
По доказанному в первом случае, левая часть неравенства представляет собой объём Vn прямоугольного параллелепипеда Pn с измерениями an, bn, cn, а правая часть – это объём Vn’ прямоугольного параллелепипеда Pn’ с измерениями an’, bn’, cn’.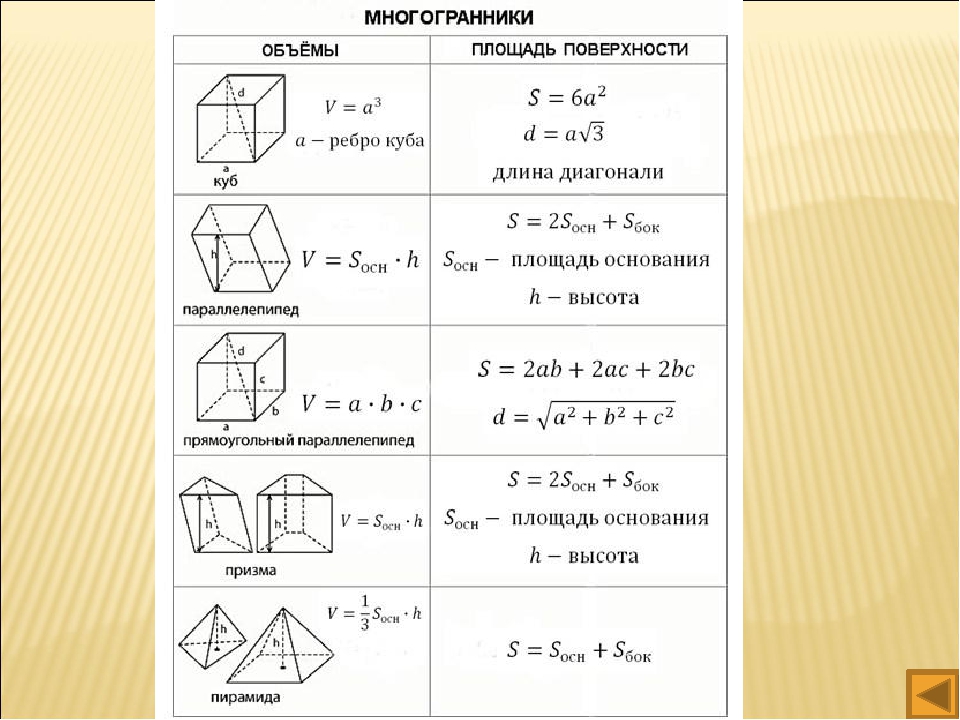 Так как параллелепипед P содержит в себе параллелепипед Pn, а сам содержится в параллелепипеде Pn’, то объём V параллелепипеда P заключён между Vn, = anbncn и Vn’= an’bn’cn’. Будем неограниченно увеличивать n. Тогда 1/10n будет становиться сколь угодно малым, и поэтому произведение an’bn’cn’ будет сколь угодно мало отличаться от числа, выраженного произведением anbncn. Отсюда следует, что число V сколь угодно мало отличается от числа, выраженного произведением anbncn, а значит, они равны.V = abc, что и требовалось доказать.
Так как параллелепипед P содержит в себе параллелепипед Pn, а сам содержится в параллелепипеде Pn’, то объём V параллелепипеда P заключён между Vn, = anbncn и Vn’= an’bn’cn’. Будем неограниченно увеличивать n. Тогда 1/10n будет становиться сколь угодно малым, и поэтому произведение an’bn’cn’ будет сколь угодно мало отличаться от числа, выраженного произведением anbncn. Отсюда следует, что число V сколь угодно мало отличается от числа, выраженного произведением anbncn, а значит, они равны.V = abc, что и требовалось доказать.
Примеры и разбор решения заданий тренировочного модуля.
№1.Длины сторон основания прямоугольного параллелепипеда равны 15 см и 20 см. Высота параллелепипеда равна диагонали основания. Найдите объём этого параллелепипеда.
Решение:
Найдём длину диагонали основания, для этого воспользуемся теоремой Пифагора:
А теперь найдём объём параллелепипеда:
V = 15 ∙ 20 ∙ 25 = 7500 см3
Ответ: V = 7500 см3.
№2.
Найдите площадь закрашенной фигуры, если объём прямоугольного параллелепипеда равен 960 см3, AB = 8 см, АА1= 20 см.
Варианты ответов:
220 см2
100 см2
400 см2
200 см2
Решение.
Найдём длину АD:
AD = 960 : 8 : 20 = 6 см
Найдём АС, воспользовавшись теоремой Пифагора:
Закрашенная фигура – прямоугольник. Вычислим его площадь: 10∙20= 200 см2.
Ответ: площадь закрашенной фигуры 200 см2.
Верный ответ: 200 см2.
Периметр, площадь и объем
1.
периметр
из
многоугольник (или любая другая замкнутая кривая, например круг) — это расстояние вокруг внешней стороны.
2.
площадь
из
простая, замкнутая, плоская кривая — это объем пространства внутри.
3.
объем
из
твердый
3
Д
форма — это количество пространства, вытесненного ею.
Некоторые формулы для общих
2
-мерные плоские фигуры и
3
-мерные тела приведены ниже.Ответов один, два,
или три измерения;
периметр
измеряется в
линейные единицы
,
площадь
измеряется в
квадратные единицы
, и
объем
измеряется в
кубические единицы
.
1 . Формулы периметра | ||
| | |
Квадратный | п знак равно 4 с | с это длина стороны квадрата. |
Прямоугольник | п знак равно 2 л + 2 Вт | л и Вт длины сторон прямоугольника (длина и ширина). |
Треугольник | а + б + с | а , б , и с являются длинами сторон. |
п знак равно а + б + а 2 + б 2 | а и б это длины двух катетов треугольника | |
Круг | р это радиус и г это диаметр. | |
| ||
| | |
Квадратный | с это длина стороны квадрата. | |
Прямоугольник | л и Вт длины сторон прямоугольника (длина и ширина). | |
Треугольник | А знак равно 1 2 б час | б и час это основание и высота |
Треугольник | А знак равно с ( с − а ) ( с − б ) ( с − с ) где с знак равно а + б + с 2 | а , б , и с это длины сторон и с это полупериметр |
Параллелограмм | б это длина основания и час это высота. | |
Трапеция | А знак равно б 1 + б 2 2 час | б 1 и б 2 — длины параллельных сторон и час расстояние (высота) между параллелями. |
Круг | А знак равно π р 2 | р это радиус. |
| ||
| | |
куб | с это длина стороны. | |
Правая прямоугольная призма | л это длина, Вт это ширина и ЧАС это высота. | |
Призма или цилиндр | А площадь основания, час это высота. | |
Пирамида или конус | А площадь основания, час это высота. | |
Сфера | р это радиус. | |
Формулы объема
( пи = = 3,141592…)
Формулы объема
Примечание: «аб» означает
«а» умножить на «б». «а
2 » означает
«а в квадрате», что равно «а», умноженному на «а».
«b 3 » означает «b в кубе», что то же самое
как «б» раз «б» раз
«б».
Будьте осторожны!! Считаются единицы.
Используйте одни и те же единицы измерения для всех измерений. Примеры
Cube = A
1 3
Прямоугольная призма = ABC
Нерегулярная призма = B H
цилиндр = B H = PI R 2 H
Pyramid = (1/3) B h
конус = (1/3) b h = 1/3 пи r 2 h
сфера = (4/3) пи r 3 2 3) пи р 1 р 2 р 3
Единицы
Объем измеряется в «кубических» единицах.Громкость
фигуры — это количество кубов, необходимых для ее полного заполнения, например
блоки в коробке.
Объем куба = сторона умножить на сторону умножить на сторону. С
каждая сторона квадрата одинакова, это может быть просто длина одного
сторона в кубе.
Если квадрат имеет одну сторону 4 дюйма, объем будет
быть 4 дюйма умножить на 4 дюйма умножить на 4 дюйма, или 64 кубических дюйма.(кубический
дюймы также могут быть записаны как 3 .)
Обязательно используйте одни и те же единицы измерения для всех измерений.
Вы не можете умножить футы на дюймы на ярды, это не дает
идеально кубическое измерение.
Объем прямоугольной призмы равен длине
сторона, умноженная на ширину, умноженная на высоту. Если ширина 4 дюйма,
длина 1 фут, а высота 3 фута, каков объем?
НЕПРАВИЛЬНО …. 4 раза 1 раз 3 = 12
ПРАВИЛЬНО …. 4 дюйма равно 1/3 фута.
Объем равен 1/3 фута, умноженному на 1 фут, умноженному на 3 фута = 1 кубический фут (или 1 куб.
футов или 1 фут 3 ).
Объемные формулы – вывод, примеры
Формула объема – это математическое выражение, используемое для нахождения полного пространства (вакуума), занятого любым трехмерным объектом. Давайте подробно разберемся с формулами объема различных трехмерных форм.
Давайте подробно разберемся с формулами объема различных трехмерных форм.
Что такое формула объема?
Формула, используемая для расчета общей кубической емкости объекта, является формулой его объема. Единица объема трехмерной формы выражается в единицах 3 или в кубических единицах. Посмотрите на приведенную ниже диаграмму формул объема, на которой показаны формулы объема соответствующих трехмерных фигур.
Давайте подробно узнаем об общих формулах объема различных форм.
Формулы объема трехмерных фигур
Теперь мы знаем, что формула объема используется для вычисления объема трехмерного объекта.В этом разделе мы узнаем о формулах объема с соответствующими размерами различных трехмерных фигур.
Объемная формула куба
Формула объема куба зависит от трех сторон куба, где все три стороны равны по размеру. Объем куба – это количество, занимаемое кубом. Общая формула объема куба дается как:
- Объем куба = a × a × a = a 3 кубических единиц, , где «a» — длина стороны куба.

- Объем формулы куба с использованием диагонали может быть задан как V = (√3×d 3 )/9, где d – длина диагонали куба.
Объемная формула прямоугольного параллелепипеда
Чтобы вычислить объем пространства, заключенного в прямоугольный параллелепипед, мы используем формулу объема прямоугольного параллелепипеда. Общая формула объема прямоугольного параллелепипеда математически выражается как:
- Объем прямоугольного параллелепипеда = площадь основания × высота в кубических единицах
- Площадь основания прямоугольного параллелепипеда = l × b квадратных единиц
- Следовательно, объем прямоугольного параллелепипеда, V = l × b × h = lbh единицы 3 , , где l, b и h представляют длину, ширину и высоту параллелепипеда.
Объемная формула конуса
Чтобы рассчитать объем пространства, занимаемого трехмерным конусом с круглым основанием радиусом r и высотой h, мы используем формулу объема конуса. Общая формула объема конуса выражается как:
Общая формула объема конуса выражается как:
Объем конуса, В = (1/3)πr 2 ч кубических единиц.
Здесь,
- ‘r’ – радиус основания (окружности) конуса
- ‘h’ — высота конуса
- π – это константа со значением 22/7 (или) 3.142.
Формула объема цилиндра
Формула объема цилиндра используется для определения количества места (вместимости), занимаемого внутри него. Мы знаем, что основанием правильного кругового цилиндра является круг, а площадь круга радиуса r равна πr 2 . Таким образом, формула объема цилиндра равна
.
Объем цилиндра = πr 2 ч кубических единиц
Здесь,
- ‘r’ — радиус основания (окружности) цилиндра
- ‘h’ — высота цилиндра
- π – это константа, значение которой равно 22/7 (или) 3.142.
Таким образом, объем цилиндра прямо пропорционален его высоте и квадрату радиуса. то есть объем цилиндра становится четырехкратным, если радиус цилиндра удваивается.
то есть объем цилиндра становится четырехкратным, если радиус цилиндра удваивается.
Объемная формула сферы
Футбольный мяч — прекрасный пример, напоминающий форму сферы. Это трехмерный твердый объект с круглой структурой. Количество воздуха, находящегося в шаре, называется объемом шара или шара.Формула объема сферы задается как:
Объем сферы = (2/3)πr 2 ч
Если диаметр сферы = 2r
Следовательно, объем сферы равен (2/3)πr 2 h = (2/3)πr 2 (2r) = (4/3)πr 3 кубических единиц
Объем сферы равен (4/3)πr 3 кубических единиц
Здесь,
- ‘r’ – радиус сферы
- ‘h’ — высота сферы
- π — константа, значение которой равно 3.142 или 22/7.
Формула объема полушария
Полушарие является половиной сферы, мы можем легко вывести формулу объема полушария, используя формулу объема сферы. Теперь, учитывая, что радиус сферы составляет r единиц, а объем сферы равен (4/3)πr 3 .
Таким образом, объем полушария можно определить как: V = ½ (4/3)πr 3
Объем полушария = (2/3)πr 3 кубических единиц
Здесь,
- ‘r’ — радиус полушария
- π — константа, значение которой равно 3.142 или 22/7.
Объемная формула призмы
Формула объема призмы определяется произведением площади основания и высоты призмы. Это математически выражается как:
Объем призмы V = B × h единиц 3 .
Здесь,
- «B» — базовая площадь в квадратных единицах
- «h» — высота призмы в единицах.
Существует семь типов призм в зависимости от формы основания призмы.Формула объема призм зависит от различных оснований призм. Ознакомьтесь с объемом призмы, чтобы понять концепцию формул объема различных призм.
Формула объема пирамиды
Объем пирамиды составляет одну треть объема призмы (т. е. их основания и высоты равны ). Таким образом,
е. их основания и высоты равны ). Таким образом,
Объем пирамиды(V) = (1/3) (Bh) единиц 3 , где
- B = площадь основания пирамиды в квадратных единицах
- h = Высота пирамиды (высота) в единицах
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций с помощью Cuemath.
Забронируйте бесплатный пробный урок
Примеры формулы объема
Пример 1: Цилиндрический резервуар имеет радиус 3 единицы и высоту 8 единиц. Используя формулу объема, найдите объем цилиндра и найдите площадь его поверхности.
Решение:
Дано: r = 3 единицы, h = 8 единиц
При подстановке значений в формулу объема цилиндра имеем
Объем цилиндра = πr 2 ч
V = π(3) 2 (8)
V = π × 9 × 8
V = 72 π
Подставив значение π = 3. 14
14
V = 72 × 3,14 = 226,08 ед. 3
Объем цилиндра 226,08 ед. 3
Пример 2: Дано, что радиус конуса равен 4 единицам, а высота конуса – 9 единицам. Используя формулу объема, определите объем конуса.
Решение:
Дано: радиус = 4 единицы и высота = 9 единиц
Формула объема конуса = (1/3)πr 2 ч.
=1/3 × 3,14 × 4 2 × 9
=1/3 × 452.16
=150,72 ед. 3
∴Объем конуса будет 150,72 ед. 3
Пример 3: Используя формулу объема куба, найдите объем прямоугольного параллелепипеда, длина которого 9 дюймов, ширина 7 дюймов, а высота 5 дюймов.
Решение: Дана длина прямоугольного параллелепипеда = 9 дюймов, ширина прямоугольного параллелепипеда = 7 дюймов и высота прямоугольного параллелепипеда = 5 дюймов.
Формула объема прямоугольного параллелепипеда = l × b × h 90 495
Подставив значения l, b и h в формулу объема, получим
V = 9 × 7 × 5
= 315
= 315 дюймов 3
∴Объем параллелепипеда будет 315 дюймов 2
Часто задаваемые вопросы о формулах объема
Какова формула объема для прямоугольного параллелепипеда?
Формула объема прямоугольного параллелепипеда: l × b × h кубических единиц.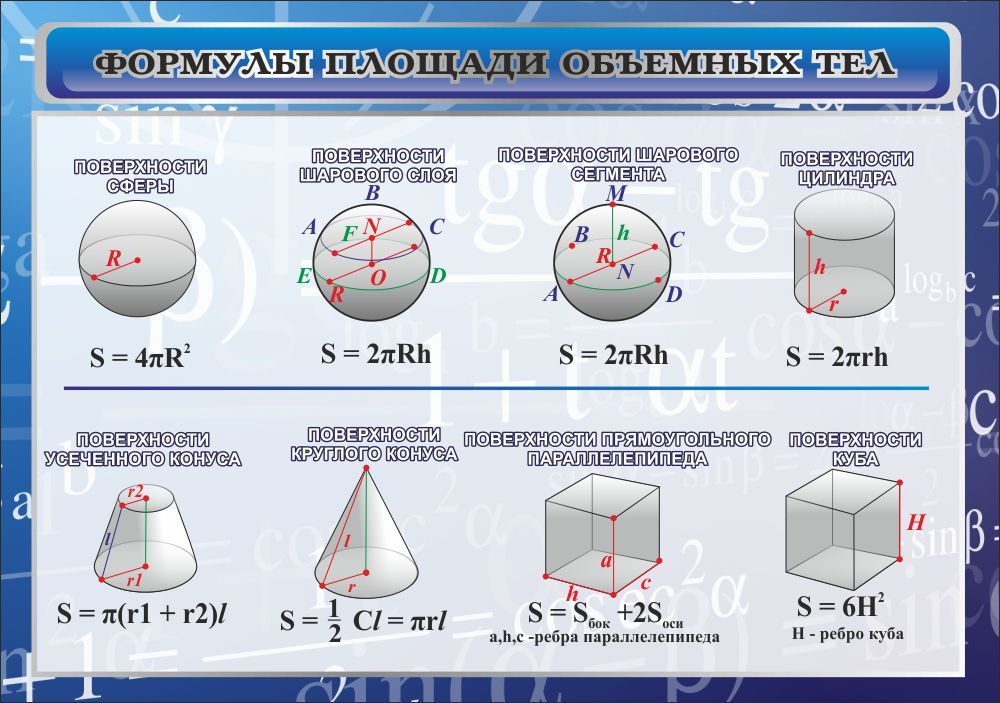 Здесь «l», «b» и «h» обозначают длину, ширину и высоту прямоугольного параллелепипеда.
Здесь «l», «b» и «h» обозначают длину, ширину и высоту прямоугольного параллелепипеда.
Какая связь между формулой объема сферы и полушария?
Формула объема полушария составляет половину формулы объема шара. Это дается как:
Объем полусферы = ½ (формула объема сферы) = ½ (4/3)πr 3 = (2/3)πr 3 кубических единиц , где «r» – радиус полусферы/сферы.
Какова формула объема конуса?
Формула объема конуса математически выражается как V = (1/3)πr 2 ч кубических единиц.Здесь «r» — радиус основания конуса, а «h» — высота конуса.
Какая связь между формулами объема призмы и пирамиды?
Формула объема пирамиды составляет 1/3 формулы объема призмы. Это дается как:
Объем пирамиды = 1/3 (формула объема призмы) = 1/3 (Bh) кубических единиц, где ‘B’ – площадь основания пирамиды/призмы, выраженная в единицах 2 и ‘h’ высота пирамиды/призмы, выраженная в единицах.
Объем — определение, формула, калькулятор, примеры
Объем — это мера вместимости объекта. Например, если чашка может вместить до краев 100 мл воды, говорят, что ее объем равен 100 мл. Объем также можно определить как объем пространства, занимаемый трехмерным объектом. Объем твердого тела, такого как куб или прямоугольный параллелепипед, измеряется путем подсчета количества содержащихся в нем единичных кубов. Лучший способ визуализировать объем — думать о нем с точки зрения пространства, заключенного/занятого любым трехмерным объектом или твердой формой.В этом можно убедиться, выполнив простое домашнее упражнение:
Например, если чашка может вместить до краев 100 мл воды, говорят, что ее объем равен 100 мл. Объем также можно определить как объем пространства, занимаемый трехмерным объектом. Объем твердого тела, такого как куб или прямоугольный параллелепипед, измеряется путем подсчета количества содержащихся в нем единичных кубов. Лучший способ визуализировать объем — думать о нем с точки зрения пространства, заключенного/занятого любым трехмерным объектом или твердой формой.В этом можно убедиться, выполнив простое домашнее упражнение:
.
- Возьмите прямоугольный лист бумаги длиной ‘ l ‘ см и шириной ‘ h ‘ см.
- Соедините противоположные стороны листа бумаги, не сгибая лист.
- Вы создали трехмерный объект, который заключает в себе пространство, из двухмерного листа.
Определение тома
Объем определяется как объем, занимаемый трехмерной твердой формой.Трудно визуализировать объем любой твердой формы, но мы определенно можем сравнить объем этих соответствующих фигур.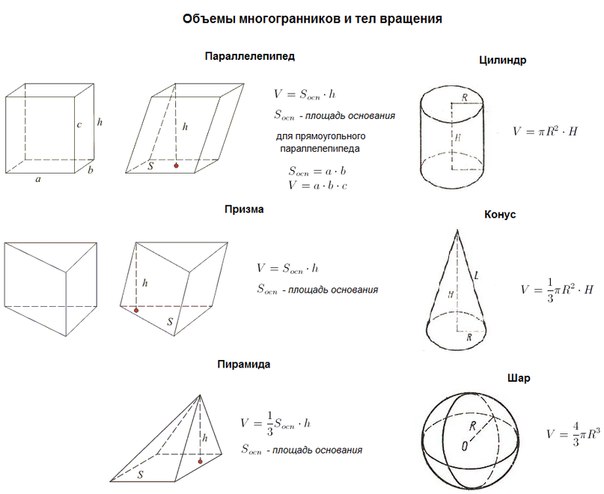 Например, объем ящика компаса больше объема помещенного в него ластика. Для расчета площади любой двумерной формы мы делим часть на равные квадратные единицы. Точно так же при вычислении объема объемных фигур мы будем делить его на равные кубические единицы. Давайте узнаем, как рассчитать объем различных твердых фигур в нашем следующем разделе.
Например, объем ящика компаса больше объема помещенного в него ластика. Для расчета площади любой двумерной формы мы делим часть на равные квадратные единицы. Точно так же при вычислении объема объемных фигур мы будем делить его на равные кубические единицы. Давайте узнаем, как рассчитать объем различных твердых фигур в нашем следующем разделе.
Объем 3D-фигур
Каждый объект в нашем окружении имеет свойство занимать пространство. Эти реальные объекты можно легко сравнить с основными трехмерными формами. Давайте посмотрим на объем этих твердых фигур в деталях.
Объем прямоугольного параллелепипеда
Предположим, у нас есть несколько прямоугольных листов длиной ‘l’ и шириной ‘ b’ . Если сложить их друг на друга до высоты ‘h’ , то получится прямоугольный параллелепипед размерами l, b, h .Это видно из следующего рисунка, на котором показаны длина, ширина (ширина) и высота образованного таким образом параллелепипеда.
Чтобы вычислить объем пространства, заключенного в этом прямоугольном параллелепипеде, мы используем формулу: Объем прямоугольного параллелепипеда = l × b × h
Объем куба
Куб — это частный случай прямоугольного параллелепипеда, у которого все три стороны равны по размеру. Если мы представим это равное значение как «а», то объем этого куба можно будет рассчитать по формуле: Объем куба = а × а × а = а³.Обратите внимание на следующий рисунок, чтобы увидеть равные стороны куба и пространство, которое он занимает.
Объем цилиндра
Точно так же, как мы построили прямоугольный параллелепипед из прямоугольников, мы можем построить цилиндр из кругов того же размера.
Цилиндр представляет собой трубчатую структуру с двумя параллельными круглыми основаниями, которые соединены изогнутой поверхностью на фиксированном расстоянии от центра. Расстояние между этими двумя основаниями и есть высота цилиндра. Если мы рассмотрим «r» как радиус круглого основания (и вершины), а «h» как высоту цилиндра, то объем цилиндра можно выразить как: Объем цилиндра = π r² h
Если мы рассмотрим «r» как радиус круглого основания (и вершины), а «h» как высоту цилиндра, то объем цилиндра можно выразить как: Объем цилиндра = π r² h
Объем пирамиды
Пирамиды имеют многоугольник в качестве основания и треугольные грани, которые сходятся на вершине. Объем пирамиды рассчитывается по формуле: Объем пирамиды = 1/3 × длина основания × ширина основания × высота пирамиды. Эту формулу также можно записать так: 1/3 × площадь основания многоугольника × высота пирамиды.
Объем конуса
Разница между конусом и пирамидой в том, что основание конуса круглое, а основание пирамиды многоугольник. Объем конуса рассчитывается по формуле: 1/3 × πr 2 ч.
Объем сферы
Объем сферы – это занимаемое ею пространство.
Объем сферы, радиус которой r равен 4/3 πr³.
Теперь, когда мы знакомы с формулами различных геометрических фигур, давайте рассмотрим различные единицы измерения объема.
Список формул объема
Ниже приведен подробный табличный список формул объема в двух словах, описывающий формулы объема для всех возможных трехмерных (теловидных) форм.
Как рассчитать объем?
Вот шагов для вычисления объема любой твердой формы:
- Определите все заданные параметры, которые являются полезными и которые необходимо заменить в соответствующей формуле объема.Например, радиус должен быть «r», а высота — «h», наклонная высота, диаметр и т. д.
- Убедитесь, что все параметры имеют одинаковые единицы измерения.
- Подставьте значения в формулу объема соответствующих фигур.
- Запишите единицы измерения в кубических единицах.
Давайте разберемся с шагами на примере.
Пример: Найдите объем прямоугольного цилиндра радиусом 25 м и высотой 1 метр. Используйте π = 3.142.
Решение:
Радиус цилиндра r = 25 м.
Его высота h = 1 метр.
Его объем цилиндра V = πr 2 h = (3,142)(25) 2 (1) = 1963,75 м 3 .
Объем баллона 1963,75 куб.м.
единиц объема
Единицей объема в СИ является кубический метр (м 3 ), поскольку объем представляет собой количество трехмерного пространства, занимаемого формой или поверхностью.Однако наиболее часто используемой единицей измерения объема является литр. Кроме того, большие и малые объемы измеряются в других единицах, таких как миллилитры (мл), пинты, галлоны и другие. В следующей таблице показаны несколько единиц, связанных с объемом, и их метрические эквиваленты.
| Боковой блок | Единица объема | Метрический эквивалент |
|---|---|---|
| Дюйм | кубических дюймов (в 3 ) | 1 куб.в = 16,387064 мл |
| Ножка | кубических футов ( 3 футов) | 1 куб. фут = 28,316846592 л фут = 28,316846592 л |
| см | Кубический сантиметр (см 3 ) | 1 кубический сантиметр = 1 мл |
| Двор | Кубический ярд (ярд 3 ) | 1 куб. ярд = 764,554857984 л 1 куб.ярд = 0,764554857984 м 3 |
В то время как стандартной единицей измерения в США является кубический ярд или кубический дюйм, более широко используемыми единицами измерения являются галлоны, пинты или жидкие унции.В следующей таблице показаны некоторые из этих единиц и их эквивалентные метрические преобразования.
| Блок | Эквивалентное преобразование |
|---|---|
| 1 пинта (pt) | 2 чашки |
| 1 кварта | 2 балла |
| 1 галлон (гал) | 3,78 литра |
| 1 литр | 1000 кубических сантиметров |
Калькулятор объема
Калькулятор объема помогает быстро и легко рассчитать объем любой заданной формы. Объем — это раздел математики, который занимается измерением емкости различных твердых тел. Попробуйте калькулятор объемов Cuemath прямо сейчас. Это онлайн-инструмент для простых и быстрых расчетов.
Объем — это раздел математики, который занимается измерением емкости различных твердых тел. Попробуйте калькулятор объемов Cuemath прямо сейчас. Это онлайн-инструмент для простых и быстрых расчетов.
☛Также проверьте:
☛Статьи по теме
Ознакомьтесь со статьями, посвященными тому различных твердых форм.
Часто задаваемые вопросы по тому
Что такое объем?
Объем — это мера вместимости объекта.Скажем, если чашка может вместить 1000 мл сока, говорят, что ее объем равен 1000 мл. В этом случае объем также можно определить как количество сока, занимаемое чашкой. Объем всегда рассчитывается путем деления емкости фигур на равные кубические единицы.
☛Загрузите сейчас, чтобы попрактиковаться.
Какая формула объема частичного конуса?
Объем частичного конуса можно рассчитать по формуле: V = 1/3 × πh(R² + Rr + r²), где «R» — радиус основания конуса, а «r» — радиус верхней поверхности.
☛ Прочтите основы здесь:
Как найти объем пирамид?
Объем пирамиды рассчитывается по формуле: V = 1/3 × площадь основания × высота.
☛ Также проверьте:
Как найти объем конуса?
Объем конуса составляет 1/3 объема цилиндра с такой же высотой и тем же основанием. Формула, используемая для нахождения объема конуса: 1/3 × π r² h; где «r» — радиус, а «h» — высота конуса.
Как найти объем цилиндра?
Объем цилиндра рассчитывается по формуле: V = площадь основания цилиндра × высота, а также представляется как: объем цилиндра = π r² h; где «r» — радиус цилиндра, а «h» — высота.
В чем разница между объемом и площадью?
Объем фигуры или твердого тела — это пространство, занимаемое им, которое также включает его высоту или глубину. Измеряется в кубических единицах.Площадь – это пространство, занимаемое поверхностью плоской формы. Измеряется в квадратных единицах.
☛ Проверьте список важных математических формул:
Каков объем мяча?
Поскольку шар является сферой, его объем будет рассчитан по формуле объема сферы. Формула объема сферы: 4/3 πr³, где «r» — радиус сферы.
Какая формула объема цилиндра?
Формула объема цилиндра = πr²h; где «r» — радиус основания цилиндра, а «h» — высота.
Как найти объем призмы?
Мы можем найти объем призмы, записав заданные размеры призмы. Затем подставьте значения в формулу объема V = B × H, где «V», «B» и «H» — это объем, площадь основания и высота призмы. Получив значение объема призмы, в конце запишите единицу объема призмы (в кубических единицах).
☛Чек:
Как найти объем бака?
Объем бака зависит от его формы.В зависимости от размера мы можем использовать приведенные ниже формулы:
- Объем прямоугольного параллелепипеда = l × b × h; где «l» — длина прямоугольного параллелепипеда, «b» — ширина (ширина) прямоугольного параллелепипеда, а «h» — высота прямоугольного параллелепипеда.

- Объем куба = a 3 , где «a» — ребро куба.
- Объем цилиндра = π r 2 ч; где «r» — радиус основания цилиндра, а «h» — высота цилиндра.
- Объем конуса = 1/3 π r² h, здесь «r» — радиус круглого основания конуса, а «h» — высота конуса.
- Объем сферы = 4/3 πr³, где r — радиус сферы.
Часто задаваемые вопросы о искусственном вскармливании: сколько и как часто (для родителей)
Независимо от того, решили ли вы кормить ребенка смесью с самого начала, докармливаете свое грудное молоко смесью или переходите с грудного молока на смесь, у вас обязательно возникнут вопросы. Вот ответы на некоторые распространенные вопросы о искусственном вскармливании.
Как часто я должен кормить своего ребенка?
Новорожденных и маленьких детей следует кормить всякий раз, когда они кажутся голодными.Это называется подачей по требованию .
После первых нескольких дней жизни большинство здоровых новорожденных, находящихся на искусственном вскармливании, кормятся примерно каждые 2–3 часа. По мере того, как они становятся больше и их животики могут вмещать больше молока, они обычно едят примерно каждые 3-4 часа. По мере того, как дети становятся старше, они привыкают к более предсказуемому режиму кормления и могут дольше ходить ночью, не нуждаясь в бутылочке.
По мере того, как они становятся больше и их животики могут вмещать больше молока, они обычно едят примерно каждые 3-4 часа. По мере того, как дети становятся старше, они привыкают к более предсказуемому режиму кормления и могут дольше ходить ночью, не нуждаясь в бутылочке.
Поговорите со своим врачом, если у вас есть опасения по поводу кормления вашего ребенка, особенно если ваш ребенок очень мал, не набирает вес или родился рано (преждевременно).
Как узнать, голоден ли мой ребенок?
Признаки того, что дети голодны, включают:
- двигают головой из стороны в сторону
- открывают рты
- высунуть язык
- прикладывание рук, пальцев и кулаков ко рту
- морщит губы, как будто хочет пососать
- снова уткнулся носом в грудь своих матерей
- , показывающий рефлекс укоренения (когда ребенок двигает ртом в направлении чего-то, что гладит или касается его щеки)
Детей следует кормить до того, как они расстроятся и заплачут. Плач — поздний признак голода. Но каждый раз, когда ваш ребенок плачет, это не из-за голода. Иногда младенцев просто нужно обнять или переодеть. Или они могут быть больны, устали, им слишком жарко или слишком холодно, они испытывают боль или колики.
Плач — поздний признак голода. Но каждый раз, когда ваш ребенок плачет, это не из-за голода. Иногда младенцев просто нужно обнять или переодеть. Или они могут быть больны, устали, им слишком жарко или слишком холодно, они испытывают боль или колики.
Сколько должен пить мой ребенок?
В первые несколько недель давайте новорожденному бутылочки объемом от 2 до 3 унций (от 60 до 90 миллилитров). Дайте больше или меньше в зависимости от сигналов голода вашего ребенка.
Вот общий взгляд на то, сколько может съедать ваш ребенок в разном возрасте:
- В среднем новорожденный выпивает около 1.5–3 унции (45–90 миллилитров) каждые 2–3 часа. Это количество увеличивается по мере того, как ваш ребенок растет и может съедать больше при каждом кормлении.
- Примерно в 2 месяца ваш ребенок может выпивать около 4–5 унций (120–150 миллилитров) каждые 3–4 часа.
- В 4 месяца ваш ребенок может выпивать около 4–6 унций (120–180 миллилитров) при каждом кормлении, в зависимости от того, как часто он ест.

- К 6 месяцам ваш ребенок может выпивать 6–8 унций (180–230 миллилитров) примерно 4–5 раз в день.
Следите за признаками того, что ваш ребенок голоден или сыт.Реагируйте на эти сигналы и дайте ребенку остановиться, когда он насытится. Сытый ребенок может сосать с меньшим энтузиазмом, останавливаться или отворачиваться от бутылочки.
Почему мой ребенок кажется более голодным, чем обычно?
По мере того, как дети растут, они начинают есть больше при каждом кормлении, а перерывы между кормлениями могут увеличиваться. Тем не менее, могут быть моменты, когда ваш малыш кажется более голодным, чем обычно.
Ваш ребенок может переживать период быстрого роста (так называемый скачок роста). Это может произойти в любое время, но в первые месяцы обычно бывает около:
.
- 7–14 дней
- от 3 до 6 недель
- 4 месяца
- 6 месяцев
В это время и всякий раз, когда ваш ребенок кажется особенно голодным, следите за сигналами голода и продолжайте кормить по требованию, увеличивая количество смеси, которую вы даете по мере необходимости.
Достаточно ли ест мой ребенок?
Иногда вы можете задаться вопросом, получает ли ваш ребенок достаточно питательных веществ для здорового роста и развития. Младенцы, которые получают достаточно еды, кажутся удовлетворенными после еды и регулярно писают и какают.
Во время осмотра вашего ребенка врач просмотрит диаграмму роста вашего ребенка, отследит его развитие и ответит на любые вопросы. Поговорите со своим врачом, если у вас есть какие-либо опасения по поводу кормления и питания вашего ребенка.
Исчисление I — Формулы площади и объема
Показать мобильное уведомление
Показать все примечания Скрыть все примечания
Похоже, вы используете устройство с «узкой» шириной экрана ( i.е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 7-6: Формулы площади и объема
В этом разделе мы выведем формулы, используемые для получения площади между двумя кривыми и объема тела вращения.
Область между двумя кривыми
Начнем с формулы для определения площади между \(y = f\left( x \right)\) и \(y = g\left( x \right)\) на интервале \(\left[ { яркий]\). Будем также считать, что \(f\left( x \right) \ge g\left( x \right)\) на \(\left[ {a,b} \right]\).
Теперь мы будем действовать так же, как и при рассмотрении проблемы площади в главе об интегралах. *\), и затем мы можем использовать прямоугольники на каждом интервале следующим образом.{{\,b}}{{f\влево(x\вправо) — g\влево(x\вправо)\,dx}}\]
*\), и затем мы можем использовать прямоугольники на каждом интервале следующим образом.{{\,b}}{{f\влево(x\вправо) — g\влево(x\вправо)\,dx}}\]
Приведенная выше формула будет работать при условии, что две функции имеют вид \(y = f\left( x \right)\) и \(y = g\left( x \right)\). Однако не все функции имеют такую форму.
Иногда нам придется работать с функциями в виде между \(x = f\left( y \right)\) и \(x = g\left( y \right)\) на интервале \(\left [ {c,d} \right]\) (интервал значений \(y\)…). Когда это происходит, вывод идентичен.{{\,d}}{{f\влево(y\вправо) — g\влево(y\вправо)\,dy}}\]
Таким образом, независимо от формы, в которой находятся функции, мы используем в основном одну и ту же формулу.
Тома для Solid of Revolution
Прежде чем вывести формулу для этого, мы, вероятно, должны сначала определить, что такое тело вращения. Чтобы получить тело вращения, мы начинаем с функции \(y = f\left( x \right)\) на интервале \(\left[ {a,b} \right]\). *\).{{\,b}}{{A\влево( x \вправо)\,dx}}\end{align*}\]
*\).{{\,b}}{{A\влево( x \вправо)\,dx}}\end{align*}\]
Значит, в этом случае объем будет интегралом площади поперечного сечения при любых \(x\), \(A\left( x \right)\). Также обратите внимание, что в этом случае площадь поперечного сечения представляет собой круг, и мы могли бы пойти дальше и получить формулу и для этого. Однако приведенная выше формула является более общей и будет работать для любого способа получения поперечного сечения, поэтому мы оставим ее как есть.
В разделах, где мы на самом деле используем эту формулу, мы также увидим, что существуют способы создания поперечного сечения, которые фактически дают площадь поперечного сечения, являющуюся функцией \(y\), а не \(x\).{{\,d}}{{A\влево(y\вправо)\,dy}}\]
Произошла ошибка при настройке пользовательского файла cookie
Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка браузера на прием файлов cookie
Существует множество причин, по которым файл cookie не может быть установлен правильно. Ниже приведены наиболее распространенные причины:
- В вашем браузере отключены файлы cookie.Вам необходимо сбросить настройки браузера, чтобы принять файлы cookie, или спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает, хотите ли вы принимать файлы cookie, и вы отказались.
Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файл cookie. - Ваш браузер не поддерживает файлы cookie. Попробуйте другой браузер, если вы подозреваете это.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г.,
браузер автоматически забудет файл cookie.Чтобы это исправить, установите правильное время и дату на своем компьютере. - Вы установили приложение, которое отслеживает или блокирует установку файлов cookie.

Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Предоставить доступ без файлов cookie
потребует от сайта создания нового сеанса для каждой посещаемой вами страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в файле cookie; никакая другая информация не фиксируется.
Как правило, в файле cookie может храниться только та информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт
не может определить ваше имя электронной почты, если вы не решите ввести его.

 п.)
п.) п. = 2 (ac + bc)
п. = 2 (ac + bc) Объем параллелепипеда.
Объем параллелепипеда.