Посчитать объем траншеи: Расчет объемов земляных работ
- Расчет объемов земляных работ
- Рассчёт объёма траншеи — онлайн калькулятор
- Онлайн-калькулятор котлована с откосами (или без них)
- Подсчёт объёмов земляных работ
- Расчёт котлована, объемов земляных работ — онлайн калькулятор
- Расчет объема земляных работ для траншеи
- Определение объемов и обмер земляных работ
- Расчет траншей или канав
- Калькулятор объема
- Калькулятор объема сферы
- Калькулятор объема конуса
- Калькулятор объема куба
- Калькулятор объема цилиндра
- Калькулятор объема прямоугольного резервуара
- Калькулятор объема капсулы
- Калькулятор объема сферической крышки
- Калькулятор объема конической ствола
- Калькулятор объема эллипсоида
- Калькулятор объема квадратной пирамиды
- Калькулятор объема трубки
- Расчетный объем | SkillsYouNeed
- Как рассчитать объем
Расчет объемов земляных работ
Траншея — это открытая выемка в земле, предназначенная для устройства ленточного фундамента, прокладки коммуникаций (водопровод, канализация, силовые кабеля, сети связи).
При устройстве ленточного фундамента ширину траншеи рекомендуется принимать на 600 мм больше ширины основания фундамента bф (для возможности выполнения монтажных работ, проход людей).
Траншея с вертикальными стенками на спланированной местности — самая простая форма выемки. В основном применяется при низкой высоте траншеи и при производстве работ в зимних условиях, когда откосы траншеи заморожены, и нет опасности обвала грунта, так же применяется при устройстве механических креплений стен выемки (распорных; консольных; консольно-распорных).
Крутизна откосов в зависимости от вида грунта и глубины выемки
| Наименование грунтов | Крутизна откосов (отношение его высоты к заложению — 1:m) при глубине выемки, м, не более | ||
| 1.5 | 3 | 5 | |
| Насыпной неуплотненный | 1:0,67 | 1:1 | 1:1,25 |
| Песчаный и гравийный | 1:0,5 | 1:1 | 1:1 |
| Супесь | 1:0,25 | 1:0,67 | 1:0,85 |
| Суглинок | 1:0 | 1:0,5 | 1:0,75 |
| Глина | 1:0 | 1:0,25 | 1:0,5 |
| Лессы и лессовидные | 1:0 | 1:0,5 | 1:0,5 |
Объем выемки траншеи можно опрделить как произведение площади поперечного сечения на длинну.
Объем обратной засыпки определяется как разность между объемом выемки и монтируемых конструкций (фундаментных блоков, труб).
Котлован — выемка в грунте, предназначенная для устройства оснований и фундаментов зданий и других инженерных сооружений.
Рассчёт объёма траншеи — онлайн калькулятор
Инструкция по расчету объема грунта траншеи
Для начала, необходимо заполнить исходные данные онлайн калькулятора в метрах:

L – это длина траншеи, зависит от назначения, например, для устройства фундамента, прокладки коммуникаций (водопровод, канализация, газопровод, силовые или слаботочные кабеля).
A – ширина верхней части траншеи, определяется возможностью работы в траншее работников обустраивающих коммуникации.
При устройстве ленточного фундамента ширину траншеи рекомендуется увеличить на 600 мм больше ширины основания фундамента (для возможности монтажа опалубки, перемещения рабочих).
B – ширина нижняя (дна), поскольку часто траншею роют с откосами, препятствующими осыпанию грунта, то ее размеры вверху и снизу могут отличаться. Разница между шириной верха и дна определяет крутизну откосов.
Если откосы не делаются и ширина постоянна вверху и внизу траншеи – введите одинаковые значения параметров А и В
H – глубина траншеи, зависит от ее целевого назначения, например для ленточного фундамента 0,5-2,5 м, согласно СНиП 3.02.01-87. Для газопровода не менее 0,8 метров до верхней точки трубы с учетом СП 62.13330.2011 (СНиП 42-01-2002), глубина прокладки водопроводных труб регламентируется СНиП 2.04.02-84 (к фактической глубине промерзания грунта необходимо прибавить минимум 0,5 метра). Минимальная глубина заложения канализации для регионов с теплым климатом составляет 0,7-0,8 м, а если зимы суровые – глубже. Для прокладки кабелей, как правило, роются траншеи глубиной порядка 0,7 м.
Стоит отметить, что иногда проще и экономичнее утеплить трубу, применить комбинированный способ устройства фундамента, (т.е. засыпка песчано-гравийной подушки, утепление и организация дренажа) и вырыть неглубокую траншею экономя время, силы и деньги за выемку, укрепление стенок и перемещение грунта.
Также укажите стоимость рытья в Вашем регионе (за 1 кубический метр) и вывоза грунта (тоже за 1 м2) после чего нажмите «Рассчитать».
Расчет объема траншеи с откосами
Калькулятор рассчитает площадь траншеи (пригодится при определении необходимого количества материала для укрепления откосов), объём траншеи даст представление, сколько грунта необходимо вынуть и переместить и подобрать оптимальный способ рытья для получения ожидаемого результата в краткий срок. Если ширина верха и дна траншеи разные, то дополнительно будут рассчитаны объемы: полезный C и откосов D. Если Вы ввели расценки подрядчиков на копку и вывоз грунта, калькулятор выдаст стоимость копания траншеи, цену перемещения грунта и общие затраты на сооружение траншеи, что позволит принять взвешенное решение – обратиться к профессионалам или копать самому.
Онлайн-калькулятор котлована с откосами (или без них)
- Монтаж фундамента
- Выбор типа
- Из блоков
- Ленточный
- Плитный
- Свайный
- Столбчатый
- Устройство
- Армирование
- Гидроизоляция
- После установки
- Ремонт
- Смеси и материалы
- Устройство
- Устройство опалубки
- Утепление
- Цоколь
- Какой выбрать
- Отделка
- Устройство
- Сваи
- Виды
- Инструмент
- Работы
- Устройство
- Расчет
Поиск
Фундаменты от А до Я.
- Монтаж фундамента
- ВсеВыбор типаИз блоковЛенточныйПлитныйСвайныйСтолбчатый
Фундамент под металлообрабатывающий станок
Устройство фундамента из блоков ФБС
Заливка фундамента под дом
Характеристики ленточного фундамента
- ВсеВыбор типаИз блоковЛенточныйПлитныйСвайныйСтолбчатый
- Устройство
- ВсеАрмированиеГидроизоляцияПосле установкиРемонтСмеси и материалыУстройствоУстройство опалубкиУтепление
Устранение трещин в стенах фундамента
Как армировать ростверк
Необходимость устройства опалубки
Как сделать гидроизоляцию цоколя
- ВсеАрмированиеГидроизоляцияПосле установкиРемонтСмеси и материалыУстройствоУстройство опалубкиУтепление
- Цоколь
- ВсеКакой выбратьОтделкаУстройство
Подсчёт объёмов земляных работ
Пользовательское соглашение
ООО «Дженерал Смета», именуемое в дальнейшем Исполнитель, предлагает на изложенных ниже условиях любому юридическому или физическому лицу, именуемому в дальнейшем Клиент, услуги по безвозмездной передаче информационных email-сообщений.
1. Термины и определения
1.1 Информационное email-сообщение – (далее – email-сообщение) – электронное письмо, отправленное Исполнителем Клиенту на его email-адрес.
1.2 Тематика сообщений – (далее – тематика) – информационное содержание email-сообщения:
1.1.1 Акции и специальные предложения касающиеся ПК «Smeta.RU».
1.1.2 Акции и специальные предложения касающиеся ПК «Система ПИР».
1.1.3 Акции и специальные предложения касающиеся официального учебного центра Исполнителя.
1.1.4 Новости и изменения касающиеся ПК «Smeta.RU».
1.1.5 Новости и изменения касающиеся ПК «Система ПИР».
1.1.6 Новости и изменения касающиеся официального учебного центра Исполнителя.
1.1.7 Новости и изменения касающиеся ценообразования в строительстве и проектировании.
1.3 Периодичность сообщений – (далее – периодичность) – средняя частота рассылки email-сообщений составляет 1 сообщение в неделю, но не более 1 сообщения в день.
2. Предмет Соглашения
2.1.Предметом Соглашения является безвозмездное оказание Исполнителем Клиенту услуг по передаче email-сообщений. Каждому Клиенту отправляются сообщения всех Тематик, указанных в п.1.2.
3. Права и обязанности сторон
3.1. Исполнитель обязуется:
3.1.1. Оказывать Клиенту Услуги с надлежащим качеством в порядке, определенном настоящим Соглашением.
3.1.2. Сохранять конфиденциальность информации, полученной от Клиента.
3.1.3. Предоставить Клиенту возможность отписаться от рассылок полностью, или частично (изменить тематику email-сообщений).
3.1.4. Немедленно прекратить рассылку email-сообщений в адрес Клиента, в случае его отказа от рассылки таких сообщений.
3.1.5. Изменить тематику email-сообщений по требованию Клиента.
3.2. Исполнитель вправе:
3.2.1. Прекратить, или приостановить оказание Услуг в любой момент, не уведомляя об этом Клиента.
4. Гарантии и конфиденциальность
4.1. Исполнитель имеет право раскрывать сведения о Клиенте только в соответствии с законодательством РФ.
4.2. Исполнитель прилагает все возможные усилия по защите, безопасному хранению и неразглашению конфиденциальной информации Клиента.
4.3. Исполнитель осуществляет сбор, хранение, обработку, использование и распространение информации в целях предоставления Клиенту необходимых услуг.
4.4. Исполнитель не продает и не передает персональную информацию о пользователях сервиса. Исполнитель вправе предоставлять доступ к персональной информации о Клиенте в следующих случаях:
4.4.1. Клиент дал на то согласие;
4.4.2. этого требует российское законодательство или органы власти в соответствии с предусмотренными законами процедурами.
5. Ответственность и ограничение ответственности
5.1. За неисполнение или ненадлежащее исполнение настоящего Соглашения Стороны несут ответственность в соответствии с законодательством РФ.
6. Расторжение и изменение условий Соглашения
6.1. Заключение настоящего Соглашения производится в целом, без каких-либо условий, изъятий и оговорок.
6.2. Фактом принятия (акцепта) Клиентом условий настоящего Соглашения является отправка своего email-адреса Исполнителю посредством специальной электронной формы на сайте Исполнителя.
6.4. Настоящее Соглашение, при условии соблюдения порядка его акцепта, считается заключенным в простой письменной форме.
6.5. Соглашение вступает в силу незамедлительно.
6.6. Исполнитель оставляет за собой право периодически изменять условия настоящего Соглашения, вводить новые Приложения к настоящему Соглашению, не публикуя уведомления о таких изменениях на сайте Исполнителя.
Расчёт котлована, объемов земляных работ — онлайн калькулятор
Инструкция для калькулятора объема и стоимости земляных работ при рытье котлована

Параметры:
X — Ширина
B — Глубина
Y — Длина
Подготовка к основательному строительству начинается с рытья котлована, который предназначается для возведения фундамента здания или сооружения, прокладки канализации, обустройства бассейна или водоёма, дренажной системы, снабжения здания или сооружения водой.
При подготовке к рытью котлована необходимо оценить количество почвы, которую необходимо будет куда-то девать – вывезти или использовать с пользой.
Выполнение проекта земляных работ и цены
Прежде чем начинать работы по рытью котлована, необходимо заранее определиться с тем, в какое место будет вывозиться вынимаемый грунт. Верхний слой, который отличается плодородными свойствами, часто применяется для облагораживания приусадебного участка, оформления клумб и цветников возле дома. Неплодородный слой может быть использован при планировке сада, огорода, в качестве подсыпки для фундамента или вывезти с участка.
Учтите, что цена на 1 м3 вынимаемой почвы будет расти по мере увеличения объ1мов траншеи.
Преимущественно потребность в вывозе почвы при рытье котлованов достаточно велика, поэтому заранее следует позаботиться об этом. Также следует учитывать запас по размеру котлована перед монтажом опалубки.
Воспользоваться услугами техники или копать котлован самостоятельно?
При выборе варианта предлагаем вам ознакомиться с особенностями каждого из них.
Ручная работа характеризуется точностью и чётким соблюдением необходимых параметров. Её стоимость будет гораздо ниже, чем аренда техники или заказ услуг по рытью котлована в специализированных агентствах. Если размер котлована — большой, а выкопать необходимо большой объём почвы, то в данном случае необходимо воспользоваться услугами техники.
Процесс в этапах
Начинать следует с определения места, где будет выкопан котлован и его разметки. Делать это рекомендуется с помощью специальных колышек, которые втыкаются по периметру участка. Между собой они соединяются шнуром яркого цвета. Помочь в максимальной точности размера ямы могут две диагонали, которые при правильной разметке будут совпадать. Использование такого метода актуально на ровном участке земли.
Существует другой вариант определения точной разметки. В небольшом отдалении от котлована вкапываются столбики, фиксирующие доски в горизонтальном положении на одном и том же уровне. На них и натягиваются шнуры. Для определения идеальной разметки необходимо постепенно перетаскивать шнуры. Также очень поможет профессиональное оборудование, которое предназначено для этих целей.
Копка котлована
Не забывайте о безопасности специалистов, копающих котлован, особенно в местности с неустойчивым или очень рыхлым грунтом. Во избежание осыпания такого грунта следует делать стенки с небольшим уклоном. Контроль стенок и дна может осуществляться с помощью уровня или рейки.
Расчет объема земляных работ для траншеи
Траншея — это выемка в земле, предназначенная для закладки ленточного фундамента или прокладки коммуникаций.
Содержание:
1. Калькулятор
2. Инструкция к калькулятору
Размеры траншеи зависят от габаритов будущего сооружения и глубины его заложения. Так, если предусматривается установка опалубки под монолитную железобетонную ленту, глубина заложения которой более 30 см, необходимо вырывать траншею шире на 600 мм с каждой стороны фундамента. К примеру, если лента имеет ширину 500 мм, ширина траншеи должна быть минимум 1700 мм. Делается это для удобства монтажа опалубки. Во всех остальных случаях траншею можно не расширять.
Ниже представлен калькулятор, с помощью которого Вы можете произвести расчет объема земляных работ для траншеи.
Данный онлайн калькулятор рассчитывает два типа выемок:
- Тип 1 — обычная прямоугольная траншея, здесь рассчитывается объем земляных работ для замкнутой или незамкнутой траншеи, а также стоимость работ по копанию и вывозу грунта при привлечении сторонних организаций.
- Тип 2 — траншея с буронабивными (буровыми) сваями, в этом случае общий объем земляных работ складывается из объема траншеи и объема выемок под сваи цилиндрического сечения; также здесь Вы можете узнать необходимое количество выемок под сваи и стоимость работ.
Калькулятор
Калькуляторы по теме:
Инструкция к калькулятору
Для того, чтобы произвести расчет необходимо выбрать тип расчета и заполнить исходные данные.
Тип 1
Длина траншеи по верху (P) — длина или сумма длин траншеи (в случае, если это периметр или траншея, сложенная из нескольких отрезков разного направления) по поверхности земли. Например, на рисунке P может равняться P1 или P2, а также может быть суммой P=P1+P2+P3+P4 (если вы хотите сосчитать всю криволинейную траншею целиком).
Длина траншеи по низу (Т) — так как зачастую траншея имеет откосы, то ее длина по верху и по низу отличаются, поэтому в этой графе Вам нужно указать длину траншеи по ее дну (Т=Т1 или Т=Т2 и т.д., или Т=Т1+Т2+Т3+Т4).
Зависит данная величина от крутизны откоса. Так, например, если глубина траншеи составляет 1м (Н=1м) и соотношение глубины траншее к длине откоса составляет 1:1 и Р1=10м, то Т1=10-1-1=8м (по метру с каждой стороны.
Ширина траншеи (В) — в графе необходимо указать ширину по дну.
Соотношение глубины траншеи к длине откоса — подразумевается крутизна откоса, которая в зависимости от вида грунта и глубины траншеи разная.
Стоимость копания и вывоза грунта — расценки подрядчиков.
Тип 2
Здесь будут рассмотрены только новые переменные. Все остальное так же, как и в Тип 1. Кроме этого, обращаю Ваше внимание, что здесь в отличие от Типа 1 отрезки каждого нового направления траншеи считаются отдельно. Другими словами Р не может равняться Р1+Р2+Р3+Р4., а только Р=Р1 или Р=Р2 и т.д.
Тип стены — выбирается для того, чтобы избежать повторного вовлечения в расчет одного и того же объема в пределах ширины траншеи. Например Р1 и Т1 — длины траншей под основную стену, а Р2 и Т2 — под не основную. В данном случае он выбирается, чтобы правильно сосчитать количество выемок под сваи.
Количество свай на отрезке — сколько вы хотите разместить свай на отрезке.
Глубина свай (F) — здесь указывается глубина свай (глубина выемки).
Отступ крайних свай (m) — отступ от края траншеи по дну до центра сваи (выемки).
Диаметр свай (D) — диаметр свай или коловорота в миллиметрах.
Шаг свай (A) — расчетный шаг выемок под буронабивные сваи. Рассчитывается в зависимости от заданного количества свай на отрезке. Обычно он равен 1,5-2,0 м. Поэтому, если например, он больше этих значений, то желательно увеличить количество свай на отрезке.
Определение объемов и обмер земляных работ
Работа землекопов оплачивается в зависимости от количества выработанного ими грунта, подсчитанного в кубических метрах. Рассмотрим несколько примеров простейших вычислений объемов работ.
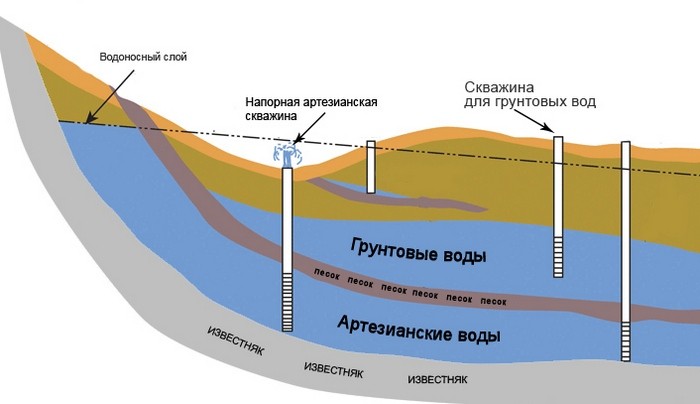
Расчет объемов рытья траншеи
Пример 1. Рабочие роют траншею с вертикальными стенками (рис. 10). За день бригада прошла 15 м траншеи. Если в начале траншеи глубина была равна 5,0 м, а в конце 4,0 м, ширина траншеи по дну и поверху — 3,0 м, то объем работ находится так: Определяем две площади поперечного сечения траншеи:
1. В месте начала работ 3*5= 15 кв.м;
2. В месте окончания работ 3*4= 12 кв.м;

Средняя площадь поперечного сечения траншеи получается, если сложить обе площади и разделить пополам:
(15+2)/2=13,5 кв.м;
Если эту среднюю площадь умножить на длину траншеи, пройденную бригадой, то получим:
13,5*15= 202,5 куб. м.
Это и будет искомый объем проделанной бригадой работы за день.
Расчет объема выемки
Пример 2. Сделана выемка для железнодорожного пути. Длины выемки — 20 м. Ширина выемки по дну — 6,0 м. Откосы сделаны с уклоном 1:2 (рис.11). Глубина выемки в одном конце 5 м, а в другом — 4 м.
Ширина выемки поверху равна ширине по дну плюс удвоенная длина заложения откоса. При откосе 1:2 заложение откоса равно двойной глубине выемки. Значит в одном конце ширина выемки поверху будет:
6+(4*2)*2=22 м,
а в другом конце:
6+(5*2)*2=26 м.
Площадь поперечного сечения выемки с откосами равна площади трапеции или половине суммы ширины по дну и ширины поверху, умноженной на высоту. Тогда площадь поперечного сечения в одном конце будет:
(6+22)/2*4=56 кв.м,
а в другом: (6+26)/2*5=80 кв.м.

Для того, чтобы получить объем, надо среднюю площадь поперечного сечения выемки умножить на длину ее (20 м).
Средняя площадь равна половине суммы площадей в начале и в конце участка выемки, т.е.:
(56+80)/2=68 кв.м.
Если помножить эту среднюю площадь на длину выемки получим:
68*20 = 1360 куб. м.
Это и есть объем выемки.
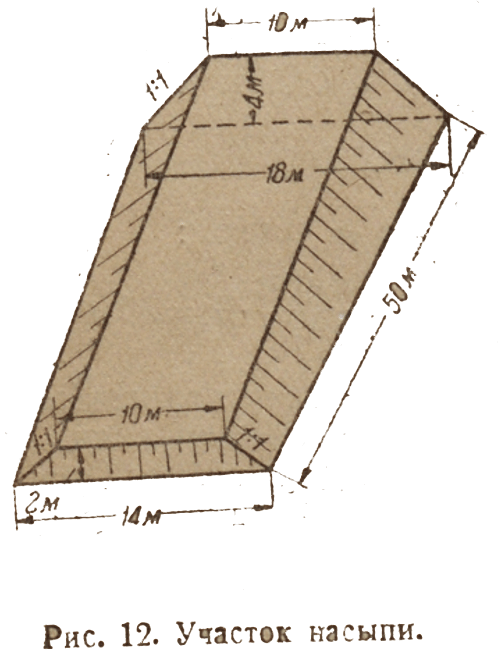
Расчет объема насыпи
Пример 3. Найти объем насыпи длиной в 50 м, если ширина ее поверху равна 10 м, крутизна откосов 1:1, высота насыпи в начале 2 м, а в конце — 4 м (рис.12). Ширина основания насыпи будет:
- в начале 10+2*(1*2)=14 м,
- в конце: 10+2*(1*4)=18 м,
а площадь поперечного сечения:
в начале: (10+14)/2*2=24 кв. м,
в конце: (10+18)/2*4=56 кв. м.
Средняя площадь поперечного сечения насыпи будет:
(24+56)/2=40 кв. м,
а объем: 40*50=2000 куб. м.
Котлованы могут быть различного очертания в плане. Объем котлованов получается, если среднюю площадь котлована умножить на его глубину.
Расчет объема котлована под здание
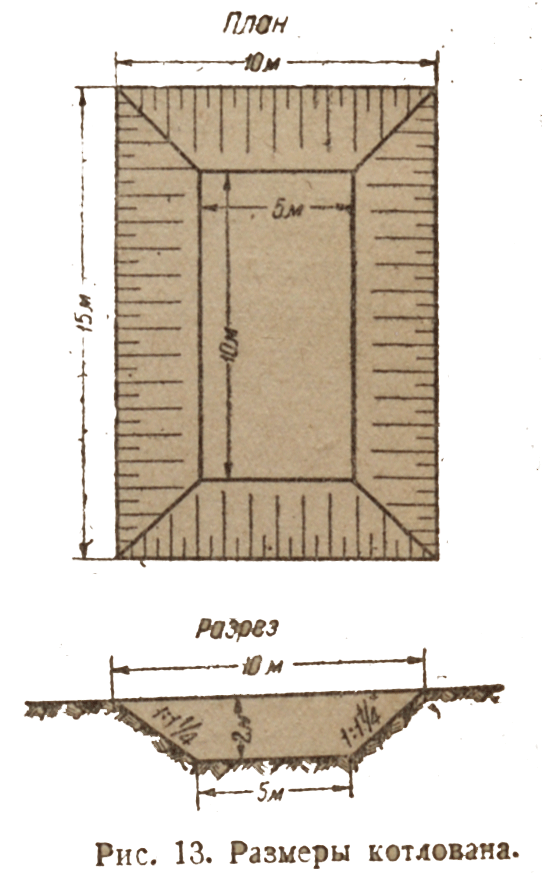
Пример 4. Найти объем котлована под здание, если глубина котлована равна 2,0 м, размеры по дну 10х5, а откосы стенок имеют крутизну 1:1, (1:1,25) рис.13. Площадь дна котлована равна 10х5=50 кв. м. Площадь верхнего сечения котлована равна:
[10+2*(1,25*2,0)]х[5+2*(1,25*2,0)]=15х10=150 кв. м.
Средняя площадь котлована равна:
(150+50)/2=100 кв. м,
а объем равен:
100*2=200 куб. м.
Расчет объема круглого котлована
Пример 5. Найти объем круглого котлована под дымовую трубу котельной. Глубина котлована — 5 м, стенки — отвесные, диаметр котлована равен 10 м. В этом случае объем равен площади дна котлована, умноженной на его глубину. Смотрите рис. 14.
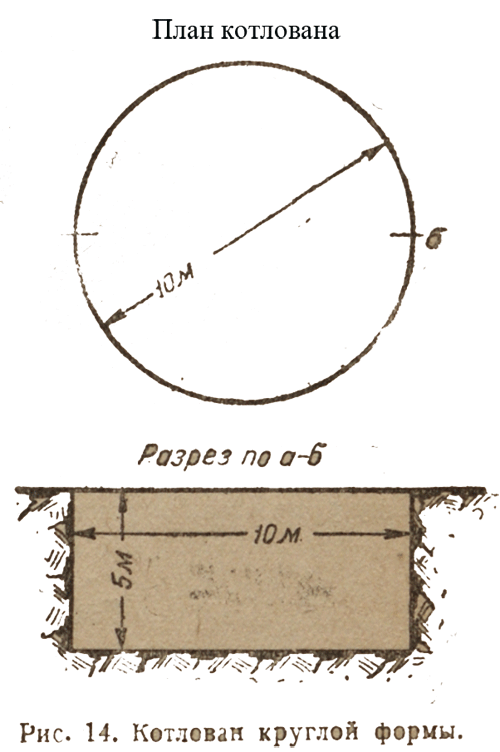
Площадь круглого дна равна диаметру его, умноженному на самого себя и еще на число 3,14 (π) и поделенному на 4, т.е.:
(10х10х3,14)/4=314/4=78,5 кв. м,
а объем котлована будет равен:
78,5х5=392,5 куб. м.
Чем более неровна поверхность земли, тем меньше должно быть расстояние между смежными поперечными профилями выемок и насыпей при подсчете их объемов.
На рис. 15 показано, в каких местах надо брать поперечные площади насыпи при сильно волнистой поверхности земли. На рис.15 1, 2, 3 и. т. д. означают те места, где надо брать площади, а l¹, l² и. т. д. — расстояние между ними.
Объем участка II насыпи будет равен площади 2+ площадь 3, деленной пополам и умноженной на расстояние l².
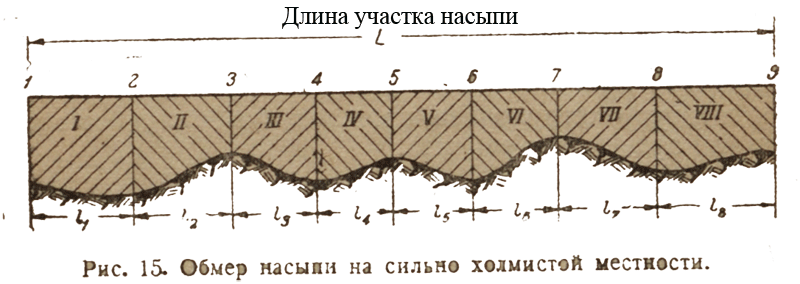
Объем всей насыпи равен сумме объемов участков I, II, III и. т. д.
Простейшими приборами для измерения длины, ширины и высоты земляного сооружения является мерная лента и рулетка.
Мерная лента делается из тонкой стали шириной 2-3 см. Длина ленты — 20 м. Лента разделена на метры, полуметры и дециметры (дециметр равен 10 см) (рис. 16).
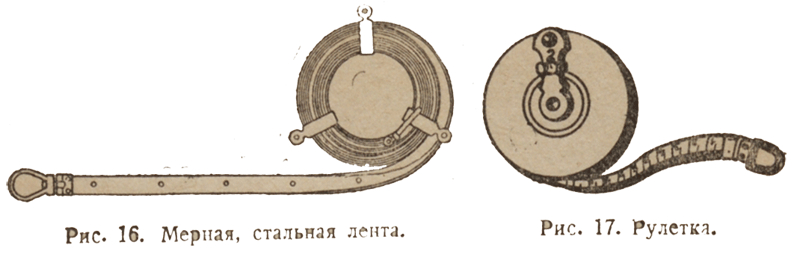
Рулетка — это тесьма длиной 5, 10 или 20 м, заключенная в футляр, в котором она наматывается на ось, пропущенную поперек футляра (рис. 17). Деления на тесьме имеются метровые, дециметровые и сантиметровые.
Оптимальным вариантов для замера в данный момент является лазерная рулетка и теодолит с нивелиром.
Мне нравитсяНе нравится
Расчет траншей или канав
Расчет траншей или канав
Указать размеры в метрах
L — общая длина траншей или канав
A — ширина вверху
B — ширина внизу
H — глубина траншеи
Программа рассчитывает объем и площадь траншеи.
Если ширина верха и низа траншеи будет разной, то дополнительно рассчитывается полезный объем C и объем наклонных участков D .
Расчет объема траншеи
Для прокладки коммуникаций, водоводов, канализации или подвала ленты на вашем участке может потребоваться рытье траншей. Можно пригласить к специалистам, а можно сделать эту работу самостоятельно. Но в обоих случаях вам необходимо знать некоторые характеристики траншеи. Рассчитайте их с помощью нашей программы. В зависимости от длины, ширины и глубины траншеи он определит ее объем и площадь. Если ширина верха и низа траншеи, также будет рассчитан и полезный объем откосов.Расчет объема траншеи поможет вам не только произвести свои работы, но и просто рассчитать стоимость земляных работ, если вы все же решили воспользоваться услугами специалистов.
Строительство траншеи
Рытье траншей можно тремя способами. Это рытье траншей вручную, с использованием ручного траншеекопателя или траншейного.
Первый случай обычно используется там, где нет доступа к спецтехнике. Это довольно трудоемкий метод рытья траншей, который очень сильно влияет на качество почвы.
Ручные траншейные машины сокращают время на такие работы. Можно купить или арендовать. Так же вы можете заказать рытье траншей в специализированной компании. Тогда это выглядит профессионально.
Экскаватор применяют там, где на участке можно достать строительную технику, а также там, где есть большой объем работ. Перед тем как арендовать экскаватор с обратной лопатой следует выяснить ширину дна траншеи, чтобы подобрать машину с размером ковша, в котором она находится.
Если вы решили рыть траншею самостоятельно, в первую очередь следует знать, что для разных видов работ требуется определенная глубина траншеи.Например, для прокладки кабеля стараются рыть траншеи глубиной около 70 см. А для канализации требуется глубокая траншея. Пока желательно, чтобы глубина была на полметра больше глубины промерзания почвы.
Ширина траншеи также влияет на вид выполняемых работ. Минимальная ширина траншеи измеряется по дну и должна соответствовать типу и размеру укладываемой в нее трубы. .
Калькулятор объема
Ниже приводится список калькуляторов объема для нескольких распространенных форм. Заполните соответствующие поля и нажмите кнопку «Рассчитать».
Калькулятор объема сферы
Калькулятор объема конуса
Калькулятор объема куба
Калькулятор объема цилиндра
Калькулятор объема прямоугольного резервуара
Калькулятор объема капсулы
Калькулятор объема сферической крышки
Для расчета укажите любые два значения ниже.
Калькулятор объема конической ствола
Калькулятор объема эллипсоида
Калькулятор объема квадратной пирамиды
Калькулятор объема трубки
Калькулятор площади сопутствующих поверхностей | Калькулятор площади
Объем — это количественная оценка трехмерного пространства, которое занимает вещество.Единицей измерения объема в системе СИ является кубический метр или м 3 . По соглашению, объем контейнера обычно определяется его вместимостью и количеством жидкости, которое он может вместить, а не объемом пространства, которое фактически вытесняет контейнер. Объемы многих форм можно рассчитать с помощью четко определенных формул. В некоторых случаях более сложные формы могут быть разбиты на более простые совокупные формы, а сумма их объемов используется для определения общего объема. Объемы других, еще более сложных фигур можно рассчитать с помощью интегрального исчисления, если существует формула для границы фигуры.Помимо этого, формы, которые нельзя описать известными уравнениями, можно оценить с помощью математических методов, таких как метод конечных элементов. В качестве альтернативы, если плотность вещества известна и однородна, объем можно рассчитать, используя его вес. Этот калькулятор вычисляет объемы для некоторых наиболее распространенных простых форм.
Сфера
Сфера — это трехмерный аналог двумерного круга. Это идеально круглый геометрический объект, который математически представляет собой набор точек, которые равноудалены от данной точки в ее центре, где расстояние между центром и любой точкой на сфере составляет радиус r .Вероятно, самый известный сферический объект — это идеально круглый шар. В математике существует различие между шаром и сферой, где шар представляет собой пространство, ограниченное сферой. Независимо от этого различия, шар и сфера имеют одинаковый радиус, центр и диаметр, и расчет их объемов одинаков. Как и в случае с кругом, самый длинный отрезок, соединяющий две точки сферы через ее центр, называется диаметром d . Уравнение для расчета объема шара приведено ниже:
EX: Клэр хочет заполнить идеально сферический воздушный шар с радиусом 0.15 футов с уксусом для борьбы с ее заклятым врагом Хильдой на воздушных шарах в предстоящие выходные. Необходимый объем уксуса можно рассчитать с помощью приведенного ниже уравнения:
объем = 4/3 × π × 0,15 3 = 0,141 фута 3
Конус
Конус — это трехмерная форма, которая плавно сужается от своего обычно круглого основания к общей точке, называемой вершиной (или вершиной). Математически конус образован так же, как круг, набором отрезков прямых, соединенных с общей центральной точкой, за исключением того, что центральная точка не входит в плоскость, содержащую круг (или другое основание).На этой странице рассматривается только случай конечного правого кругового конуса. Конусы, состоящие из полуосей, некруглых оснований и т. Д., Которые простираются бесконечно, не рассматриваются. Уравнение для расчета объема конуса выглядит следующим образом:
, где r — радиус, а h — высота конуса
EX: Би полна решимости выйти из магазина мороженого, потратив свои с трудом заработанные 5 долларов. Хотя она предпочитает обычные сахарные рожки, вафельные рожки, несомненно, больше.Она определяет, что на 15% предпочитает обычные сахарные рожки вафельным рожкам, и ей необходимо определить, превышает ли потенциальный объем вафельного рожка на ≥ 15% больше, чем вафельный рожок. Объем вафельного рожка с круглым основанием радиусом 1,5 дюйма и высотой 5 дюймов можно рассчитать с помощью следующего уравнения:
объем = 1/3 × π × 1,5 2 × 5 = 11,781 дюйм 3
Беа также вычисляет объем сахарного рожка и обнаруживает, что разница составляет <15%, и решает купить сахарный рожок.Теперь все, что ей нужно сделать, это использовать свой ангельский детский призыв, чтобы заставить посох выливать мороженое из контейнеров в ее конус.
Куб
Куб является трехмерным аналогом квадрата и представляет собой объект, ограниченный шестью квадратными гранями, три из которых пересекаются в каждой из его вершин, и все они перпендикулярны своим соответствующим смежным граням. Куб является частным случаем многих классификаций геометрических фигур, включая квадратный параллелепипед, равносторонний кубоид и правый ромбоэдр.Ниже приведено уравнение для расчета объема куба:
объем = 3
где a — длина ребра куба
EX: Боб, который родился в Вайоминге (и никогда не покидал штат), недавно посетил свою исконную родину Небраску. Пораженный великолепием Небраски и окружающей средой, непохожей на какие-либо другие, с которыми он раньше сталкивался, Боб знал, что ему нужно привезти с собой домой часть Небраски. У Боба есть чемодан кубической формы с длиной по краям 2 фута, и он рассчитывает объем почвы, который он может унести домой, следующим образом:
объем = 2 3 = 8 футов 3
Цилиндр
Цилиндр в его простейшей форме определяется как поверхность, образованная точками на фиксированном расстоянии от данной прямой оси.Однако в обычном использовании термин «цилиндр» относится к правильному круговому цилиндру, где основания цилиндра представляют собой окружности, соединенные через их центры осью, перпендикулярной плоскостям его оснований, с заданной высотой h и радиусом r . Уравнение для расчета объема цилиндра показано ниже:
объем = πr 2 ч
где r — радиус, а h — высота резервуара
EX: Кэлум хочет построить замок из песка в гостиной своего дома.Поскольку он является твердым сторонником утилизации отходов, он извлек три цилиндрических бочки с незаконной свалки и очистил бочки от химических отходов, используя средство для мытья посуды и воду. Каждая бочка имеет радиус 3 фута и высоту 4 фута, и Кэлум определяет объем песка, который каждая может вместить, используя следующее уравнение:
объем = π × 3 2 × 4 = 113.097 футов 3
Он успешно построил замок из песка в своем доме и в качестве дополнительного бонуса ему удалось сэкономить электроэнергию на ночном освещении, так как его замок из песка светится ярко-зеленым в темноте.
Прямоугольный бак
Прямоугольный резервуар — это обобщенная форма куба, стороны которого могут иметь разную длину. Он ограничен шестью гранями, три из которых пересекаются в его вершинах, и все они перпендикулярны своим соответствующим смежным граням. Уравнение для расчета объема прямоугольника показано ниже:
объем = длина × ширина × высота
EX: Дарби любит торт. Она ходит в спортзал по 4 часа в день, каждый день, чтобы компенсировать свою любовь к торту.Она планирует отправиться в поход по тропе Калалау на Кауаи, и, хотя она в очень хорошей форме, Дарби беспокоится о своей способности пройти этот маршрут из-за отсутствия торта. Она решает упаковать только самое необходимое и хочет набить свою идеально прямоугольную упаковку длиной, шириной и высотой 4 фута, 3 фута и 2 фута соответственно тортом. Точный объем торта, который она может поместить в свою упаковку, рассчитан ниже:
объем = 2 × 3 × 4 = 24 фута 3
Капсула
Капсула — это трехмерная геометрическая форма, состоящая из цилиндра и двух полусферических концов, где полусфера — это полусфера.Отсюда следует, что объем капсулы можно рассчитать, объединив уравнения объема для сферы и правого кругового цилиндра:
| объем = πr 2 ч + | πr 3 = πr 2 ( | р + з) |
, где r — радиус, а h — высота цилиндрической части
EX: Имея капсулу радиусом 1,5 фута и высотой 3 фута, определите объем растопленного молочного шоколада, который Джо может унести в капсуле времени, которую он хочет похоронить для будущих поколений на пути к самопознанию. Гималаи:
объем = π × 1.5 2 × 3 + 4/3 × π × 1,5 3 = 35,343 фута 3
Сферический колпачок
Сферический колпачок — это часть сферы, которая отделена от остальной сферы плоскостью. Если плоскость проходит через центр сферы, сферическая крышка называется полусферой. Существуют и другие различия, включая сферический сегмент, где сфера сегментируется двумя параллельными плоскостями и двумя разными радиусами, где плоскости проходят через сферу. Уравнение для расчета объема сферической крышки выводится из уравнения для сферического сегмента, где второй радиус равен 0.Относительно сферической крышки, указанной в калькуляторе:
Имея два значения, калькулятор вычисляет третье значение и объем. Уравнения для преобразования между высотой и радиусом показаны ниже:
Для r и R : h = R ± √R 2 — r 2
Для R и h : r = √2Rh — h 2
где r — радиус основания, R — радиус сферы, а h — высота сферической крышки.
EX: Джек действительно хочет победить своего друга Джеймса в игре в гольф, чтобы произвести впечатление на Джилл, и вместо того, чтобы тренироваться, решает саботировать мяч для гольфа Джеймса.Он отрезает идеальную сферическую крышку от верхней части мяча для гольфа Джеймса и должен рассчитать объем материала, необходимый для замены сферической крышки и перекоса веса мяча для гольфа Джеймса. Учитывая, что мяч для гольфа Джеймса имеет радиус 1,68 дюйма, а высота сферической крышки, которую срезал Джек, составляет 0,3 дюйма, объем можно рассчитать следующим образом:
объем = 1/3 × π × 0,3 2 (3 × 1,68 — 0,3) = 0,447 дюйма 3
К несчастью для Джека, за день до игры Джеймс получил новую партию мячей, и все усилия Джека были напрасны.
Коническая Frustum
Усеченный конус — это часть твердого тела, которая остается, когда конус рассекается двумя параллельными плоскостями. Этот калькулятор рассчитывает объем специально для правильного кругового конуса. Типичные конические усики, встречающиеся в повседневной жизни, включают абажуры, ведра и некоторые стаканы для питья. Объем усеченного правого конуса рассчитывается по следующей формуле:
| объем = | πh (r 2 + rR + R 2 ) |
где r и R — радиусы оснований, h — высота усеченного конуса
EX: Би успешно приобрела мороженое в сахарном рожке и только что съела его так, что мороженое остается упакованным внутри рожка, а поверхность мороженого находится на уровне и параллельно плоскости отверстия рожка.Она собирается начать есть свой рожок и оставшееся мороженое, когда ее брат хватает ее рожок и откусывает часть дна ее рожка, которая идеально параллельна ранее единственному отверстию. У Би теперь остается конусообразная усеченная вершина, из которой вытекает мороженое, и ей необходимо рассчитать объем мороженого, который она должна быстро съесть, учитывая высоту усеченной кости 4 дюйма с радиусами 1,5 и 0,2 дюйма:
объем = 1/3 × π × 4 (0,2 2 + 0,2 × 1,5 + 1,5 2 ) = 10.849 из 3
Эллипсоид
Эллипсоид является трехмерным аналогом эллипса и представляет собой поверхность, которую можно описать как деформацию сферы посредством масштабирования элементов направления. Центр эллипсоида — это точка, в которой пересекаются три попарно перпендикулярные оси симметрии, а отрезки прямых, ограничивающие эти оси симметрии, называются главными осями. Если все три имеют разную длину, эллипсоид обычно называют трехосным.Уравнение для расчета объема эллипсоида выглядит следующим образом:
, где a , b и c — длины осей
EX: Хабат любит есть только мясо, но его мать настаивает на том, что он ест слишком много, и позволяет ему есть столько мяса, сколько он может уместить в булочке в форме эллипса. Таким образом, Хабат выдалбливает булочку, чтобы максимально увеличить объем мяса, который он может уместить в своем сэндвиче. Учитывая, что его булочка имеет длину оси 1,5 дюйма, 2 дюйма и 5 дюймов, Хабат рассчитывает объем мяса, который он может уместить в каждой полой булочке, следующим образом:
объем = 4/3 × π × 1.5 × 2 × 5 = 62,832 дюйма 3
Квадратная пирамида
Пирамида в геометрии — это трехмерное твердое тело, образованное путем соединения многоугольного основания с точкой, называемой его вершиной, где многоугольник — это форма на плоскости, ограниченная конечным числом отрезков прямой. Есть много возможных многоугольных оснований для пирамиды, но квадратная пирамида — это пирамида, в которой основание представляет собой квадрат. Другое отличие пирамид заключается в расположении вершины. У правых пирамид есть вершина, которая находится прямо над центром тяжести ее основания.Независимо от того, где находится вершина пирамиды, если ее высота измеряется как перпендикулярное расстояние от плоскости, содержащей основание, до ее вершины, объем пирамиды может быть записан как:
Объем обобщенной пирамиды:
.
Расчетный объем | SkillsYouNeed
На этой странице объясняется, как рассчитать объем твердых объектов, то есть насколько вы можете поместиться в объект, если, например, вы заполните его жидкостью.
Площадь — это мера того, сколько места находится внутри двухмерного объекта (подробнее см. Нашу страницу: Расчет площади).
Объем — это мера пространства внутри трехмерного объекта. Наша страница, посвященная трехмерным формам, объясняет основы таких форм.
В реальном мире вычисление объема, вероятно, не то, что вы будете использовать так часто, как вычисление площади.
Однако это все еще может быть важным. Возможность рассчитать объем позволит вам, например, определить, сколько у вас есть места для упаковки при переезде, сколько офисного пространства вам нужно или сколько варенья вы можете уместить в банку.
Это также может быть полезно для понимания того, что имеют в виду средства массовой информации, когда они говорят о пропускной способности плотины или течении реки.
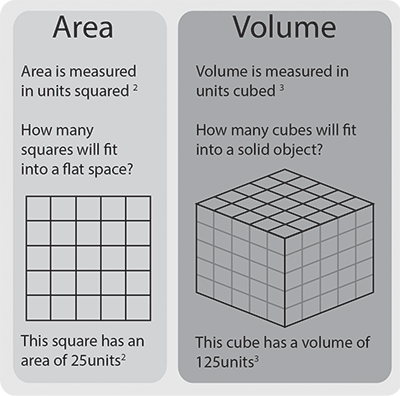
Примечание к единицам
Площадь выражается в квадратных единицах, потому что это два измерения, умноженные вместе.
Объем выражается в кубических единицах, потому что это сумма трех измерений (длина, ширина и глубина), умноженных вместе. Кубические единицы включают см 3 , м 3 и кубические футы.
ВНИМАНИЕ!
Объем также можно выразить как вместимость по жидкости.
Метрическая система
В метрической системе объем жидкости измеряется в литрах, что напрямую сопоставимо с кубическим размером, поскольку 1 мл = 1 см. 3 .1 литр = 1000 мл = 1000 см 3 .
Британская / английская система
В британской системе мер эквивалентными являются жидкие унции, пинты, кварты и галлоны, которые нелегко перевести в кубические футы. Поэтому лучше всего придерживаться жидких или твердых единиц объема.
Подробнее см. На нашей странице Системы измерения
Основные формулы для расчета объема
Объем твердых тел на основе прямоугольников
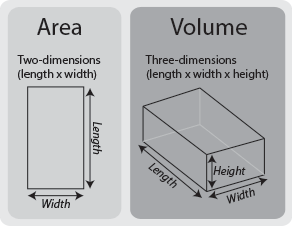
В то время как основная формула для площади прямоугольной формы — длина × ширина, основная формула для объема — длина × ширина × высота.
То, как вы относитесь к различным размерам, не меняет расчет: вы можете, например, использовать «глубину» вместо «высоты». Важно то, что все три измерения умножаются. Вы можете умножать в любом порядке, поскольку это не изменит ответ (подробнее см. Нашу страницу о умножении ).
Коробка размером 15 см в ширину, 25 см в длину и 5 см в высоту имеет объем:
15 × 25 × 5 = 1875 см 3
Объем призм и цилиндров
Эта базовая формула может быть расширена для охвата цилиндров и призм .Вместо прямоугольного конца у вас просто другая форма: круг для цилиндров, треугольник, шестиугольник или любой другой многоугольник для призмы.
Фактически, для цилиндров и призм объем — это площадь одной стороны, умноженная на глубину или высоту формы.
Таким образом, основная формула для определения объема призм и цилиндров:
Площадь формы торца × высота / глубина призмы / цилиндра.
Объем конусов и пирамид
Тот же принцип, что и выше (ширина × длина × высота), выполняется для расчета объема конуса или пирамиды, за исключением того, что, поскольку они достигают точки, объем составляет лишь часть от общего количества, которое было бы, если бы они продолжались. в той же форме насквозь.
Объем конуса или пирамиды составляет ровно одну треть от объема коробки или цилиндра с таким же основанием.
Таким образом, формула:
Площадь основания или торца × высота конуса / пирамиды × 1 / 3
Вернитесь на нашу страницу Расчет площади , если вы не можете вспомнить, как рассчитать площадь круга или треугольника.
Например, чтобы вычислить объем конуса с радиусом 5 см и высотой 10 см:
Площадь внутри круга = πr2 (где π (пи) приблизительно равно 3.14 и r — радиус круга).
В этом примере площадь основания (круга) = πr 2 = 3,14
× 5 × 5 = 78,5 см 2 .78,5 × 10 = 785
785 × 1/3 = 261,6667 см 3

Объем сферы
Как и в случае с кругом, вам нужно π (пи), чтобы вычислить объем сферы.
Формула: 4/3 × π × радиус 3 .
Вам может быть интересно, как вычислить радиус шара.Если не просунуть в него спицу (эффективный, но конечный для мяча!), Есть более простой способ.
Вы можете измерить расстояние вокруг самой широкой точки сферы напрямую, например, с помощью рулетки. Этот круг является окружностью и имеет тот же радиус, что и сама сфера.
Длина окружности вычисляется как радиус 2 x π x.
Чтобы вычислить радиус из окружности, вы:
Разделите окружность на (2 x π) .
Рабочие примеры: Расчет объема
Пример 1
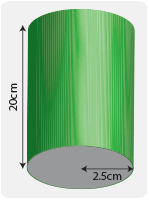
Вычислите объем цилиндра длиной 20 см, круговой конец которого имеет радиус 2,5 см.
Сначала обработайте площадь одного из круглых концов цилиндра.
Площадь круга равна πr 2 (π × радиус × радиус). π (пи) приблизительно равно 3,14.
Таким образом, площадь конца равна:
3.14 x 2,5 x 2,5 = 19,63 см 2
Объем — это площадь конца, умноженная на длину, и, следовательно, составляет:
19,63 см 2 x 20 см = 392,70 см 3
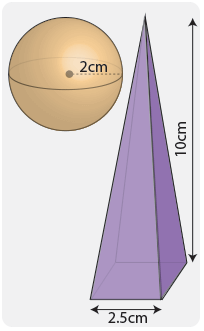
Пример 2
Что больше по объему: сфера радиусом 2 см или пирамида с основанием 2,5 см в квадрате и высотой 10 см?
Сначала определим объем сферы .
Объем сферы составляет 4/3 × π × радиус 3 .
Таким образом, объем сферы:
4 ÷ 3 x 3,14 × 2 × 2 × 2 = 33,51 см 3
Затем рассчитайте объем пирамиды .
Объем пирамиды равен 1/3 площади основания × высоты.
Площадь основания = длина × ширина = 2,5 см × 2,5 см = 6,25 см 2
Объем, следовательно, равен 1/3 x 6,25 × 10 = 20.83см 3
Таким образом, сфера больше по объему, чем пирамида.
Расчет объема твердых тел неправильной формы
Точно так же, как вы можете вычислить площадь неправильных двумерных форм, разбив их на правильные, вы можете сделать то же самое для вычисления объема неправильных твердых тел. Просто разделите твердое тело на более мелкие части, пока не получите только твердые тела, с которыми вы сможете легко работать.
Рабочий пример
Рассчитайте объем водяного баллона общей высотой 1 м, диаметром 40 см и полусферической верхней частью.
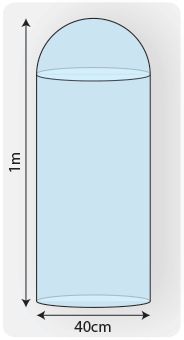
Сначала вы делите фигуру на две части: цилиндр и полусферу (полусферу).
Объем сферы составляет 4/3 × π × радиус 3 . В этом примере радиус составляет 20 см (половина диаметра). Поскольку верхняя часть полусферической формы, ее объем будет вдвое меньше полной сферы. Таким образом, объем данного участка формы:
.
0,5 × 4/3 × π × 203 = 16,755,16 см 3
Объем цилиндра равен площади основания × высоте.Здесь высота цилиндра — это общая высота за вычетом радиуса сферы, которая составляет 1 м — 20 см = 80 см. Площадь базы 2 грн.
Таким образом, объем цилиндрического сечения данной формы равен:
80 × π × 20 × 20 = 100 530,96 см 3
Таким образом, общий объем этого резервуара для воды составляет:
100 530,96 + 16 755,16 = 117 286,12 см 3 .
Это довольно большое число, поэтому вы можете преобразовать его в 117.19 литров путем деления на 1000 (поскольку в литре 1000 см 3 ). Однако вполне правильно выразить его как cm 3 , поскольку задача не требует, чтобы ответ был выражен в какой-либо конкретной форме.
В заключение…
Используя эти принципы, если необходимо, теперь вы сможете рассчитать объем практически всего в своей жизни, будь то упаковочный ящик, комната или водяной баллон.
.
Как рассчитать объем
Расчет объема
Объем измеряется в кубах (или кубических единицах).
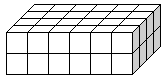
Сколько кубиков в этой прямоугольной призме (кубоиде)?
Мы можем считать кубики, хотя быстрее вычислить длину, ширину и высоту и использовать умножение. Прямоугольная призма выше имеет объем 48 кубических единиц.
Объем прямоугольной призмы = длина x ширина x высота
Примеры расчета площади прямоугольника
Нам нужно сделать два умножения, чтобы вычислить объем.Мы вычисляем площадь одной грани (или стороны) и умножаем ее на ее высоту. Примеры ниже показывают, как это можно сделать тремя способами.
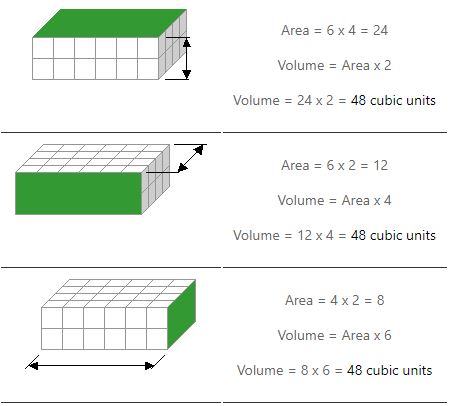
Обратите внимание, как мы получаем один и тот же ответ, независимо от того, какой стороной мы находим область.
Когда ваш ребенок начинает работать с площадью и периметром, он или она обычно работает с двумя измерениями — квадратами, прямоугольниками, треугольниками и т. Д., Которые показаны на бумаге плоскими — нет глубины или третьего измерения. Работа с объемом действительно включает 3 измерения.Убедитесь, что ваш ребенок знает об этом и не думает о кубах и других трехмерных фигурах, показанных на бумаге, просто как о еще одной «фигуре на странице». Покажите им настоящие коробки и покажите, как их можно нарисовать (или изобразить) на двухмерном листе бумаги. Другими словами, убедитесь, что существует связь между тем, что написано на бумаге, и тем, что она представляет в реальном мире.
Убедитесь, что вашего ребенка не смущает использование громкости , когда речь идет о громкости.
Единицы измерения объема
Есть очень большие различия между единицами измерения объема.Например, в 1 метре 100 сантиметров, а в кубическом метре 1000000 (да, 1 миллион) кубических сантиметров.
Почему большая разница? Потому что по объему у нас есть не только длина; у нас есть длина, ширина и высота. Пример кубика сахара ниже показывает это.
Сколько сахара? 1 м 3 или 1000000 см 3
Подумайте о наполнении очень большой коробки (шириной 1 метр, длиной 1 метр и высотой 1 метр) кубиками сахара (с каждой стороной 1 сантиметр).
 | Шаг 1: один ряд вдоль дна коробки — , что составляет 100 кубиков сахара |
| Шаг 2: накройте остальную часть основания коробки — , что даст в общей сложности 100 рядов с 100 кубиками сахара в каждом. 100 x 100 = 10 000 сахара кубика на дне большой коробки. | |
| Шаг 3: Повторите это 99 раз, пока не будет слоев по 10 000 кубов, уложенных стопкой в 100 слоев. 10 000 x 100 = 1 000 000 кубиков сахара |
1000000 см 3 в 1 м 3 — будьте осторожны, чтобы не было слишком много сахара!
Есть другие единицы измерения объема; кубические дюймы, кубические футы, кубические ярды — все это единицы измерения объема.Миллилитры, литры, галлоны также используются, особенно при измерении жидкостей.
| Не забывайте крошечный 3 |
| Пишем кубические размеры с помощью маленькой 3 рядом с единицей. Мы пишем mm 3 , cm 3 , m 3 , km 3 , cm 3 Можно сказать «85 сантиметров в кубе» или «85 кубических сантиметров» |
Примеры расчета объема прямоугольных призм
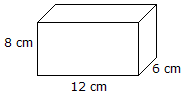 | Объем = длина x ширина x высота Объем = 12 см x 8 см x 6 см = 576 см 3 |
| Объем = длина x ширина x высота Объем = 20 м x 2 м x 2 м = 80 м 3 | |
 | Объем = длина x ширина x высота Объем = 10 м x 4 м x 5 м = 200 м 3 |
Объем цилиндра
Для вычисления объема цилиндра нужно умножить площадь основания на высоту цилиндра.Основание цилиндра круглое, а формула для определения площади круга: площадь круга = πr 2 . Здесь больше о площади круга.
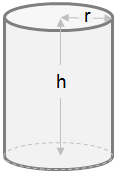 | Объем = Площадь основания x Высота Объем = πr 2 x h Объем = πr 2 h |
Примечание: в приведенных ниже примерах мы будем использовать 3,14 как приблизительное значение для π (Pi).
Пример расчета объема цилиндра
 Размеры указаны в см. | Объем = πr 2 ч Объем = 3,14 x 3 x 3 x 8 Объем = 226,08 см 3 |
Объем конуса
Объем конуса равен одной трети объема цилиндра с соответствующей высотой и площадью основания. Это дает формулу для объема конуса, как показано ниже.
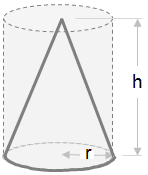 | Объем = 1/3 πr 2 ч |
Пример расчета объема конуса
 Размеры указаны в см. | Объем = 1/3 πr 2 ч Объем = 1/3 x 3,14 x 2 x 2 x 7 Объем = 29,31 см 3 |
Объем сферы
Формула объема шара приведена ниже.
 | Объем = 4/3 πr 3 |
Пример расчета объема сферы
 Размеры указаны в см. | Объем = 4/3 πr 3 Объем = 4/3 x 3,14 x 4 x 4 x 4 Объем = 267,95 см 3 |
Рабочие листы для печати
Используйте приведенную ниже таблицу, чтобы попрактиковаться в вычислении объемов.
Здесь вы найдете другие рабочие листы геометрии по периметру, площади и т. Д.
.
