Преднапряженная балка: Вы точно человек?
- Уникальная технология изготовления мостовых преднапряжённых балок в построечных условиях с помощью индивидуальных опалубочных форм
- Предварительно напряженные железобетонные конструкции: использование
- Расчет балки из предварительно–напряженного железобетона — Студопедия
- Справочник проектировщика промышленных, жилых и общественных зданий и сооружений. Расчетно-теоретический. 1960 г. Уманский А.А.
- 4. Предварительно напряженные конструкции
- Преднапряженная составная деревянная балка
- Дизайн моста | Конструкция сборных бетонных мостовых балок только в соответствии с BS 5400
- Суммарные напряжения в предварительно напряженной балке
- Руководство по проектированию двутавровых балок из предварительно напряженного бетона и втулок TxGirder
- Выбор типа моста
- Электронное уведомление PENNDOT
- Опалубка для бетона
- Двусторонняя конструкция с постнатяжением
- ГЕОМЕТРИЧЕСКИЙ ДИЗАЙН CIVL 3161
- 9.3 Двусторонние плиты (Часть I)
- Терминология Safe & Sound Bridge
- ПРИМЕР КОНСТРУКЦИИ ПОДНОЖКИ
- Балка. Армирование. Проект 07.12.02
- 16. Балочно-перекрытие.
- Раздел А Ферма крыши
- CH. 2 НАГРУЗКИ НА ЗДАНИЯ
- Стальные балки и балки
- КОНКУРС PCI BIG BEAM
- Камбер, недобрая кривая
- ПРОДУКТ И ИНЖЕНЕРНОЕ РУКОВОДСТВО
- TSL профессиональные услуги
- Глава 6 СИСТЕМЫ КРЫШИ-ПОТОЛКА
- ПРИМЕРЫ STRUSOFT ПРЕДНАПРЯЖЕНИЕ 6.4.
- КРАТКОЕ ОПИСАНИЕ ГЛАВА 6
- ГЛАВА 4 СИСТЕМЫ ДРЕНАЖНЫХ СИСТЕМ
- Системы ливневого дренажа 11.9-1
- Выбор профиля алюминиевых систем
- — Prestress Services Industries, LLC
- Основы предварительно напряженного бетонного моста (с решенным примером)
- PPT — Мониторинг предварительно напряженного бетонного моста с коробчатой балкой на предмет перегрузок Презентация в PowerPoint
Уникальная технология изготовления мостовых преднапряжённых балок в построечных условиях с помощью индивидуальных опалубочных форм
- ПСК-Строитель
- О компании
- Новости
- Уникальная технология изготовления мостовых преднапряжённых балок в построечных условиях с помощью индивидуальных опалубочных форм
Многие годы одним из основных направлений деятельности компании «ПСК-Строитель» является устройство системы преднапряжения в конструкции мостов, эстакад и путепроводов.
Применение технологии преднапряжения при монолитном строительстве пролетов существенно уменьшает деформации и препятствует образованию трещин, что особенно важно, учитывая высокие эксплуатационные нагрузки дорожных развязок. Используя технологию «преднапряжение на бетон, со сцеплением» прямо на строительной площадке при помощи модульной опалубочной системы, которую компания «ПСК-Строитель» сделает по вашему проекту необходимой конфигурации, можно изготовить преднапряженный железобетонный мостовой пролет.
Для начала работ необходимо организовать любое твёрдое основание в непосредственной близости от стройплощадки (например, при помощи стандартных ЖБИ-панелей для стен), развернуть быстро-монтируемый каркасно-тентовый ангар. При этом размер временного завода-ангара может быть очень небольшими, а высота всей конструкции не будет превышать 5 метров. При помощи мини-крана, опалубка устанавливается на высоту 1,5-2 метра и армируется ненапрягаемой арматурой. Посредством каналообразователей формируютсквозные каналы в которые укладываются напрягаемые пучки, состоящие из стальных семипроволочных канатов, устанавливаются анкеры. После процесса бетонирования и набора бетоном определенной прочности, происходит натяжение стальных канатов гидравлическими домкратами. Далее внутренняя часть каналообразователей, заполняется специальным быстротвердеющим инъекционным раствором. Демонтаж опалубочной системы прост и удобен. И обеспечивается с помощью стандартных винтовых замков-стяжек, система устанавливается на стандартные опоры-тележки, благодаря которым форму можно откатить и быстро демонтировать краном. После демонтажа опалубки включаются инфракрасные электронагреватели. За счёт данного термопрогрева опалубки можно не использовать дорогостоящие, дополнительные процедуры, применяемые на ЖБИ-заводах: пар, паропровод, прогревочный провод. Всего 4 часа для подъёма температуры, 12 часов выдержки, 5-6 часов остывания (в общей сложности время изготовления занимает менее суток) и монолитная преднапряжённая балка готова
После демонтажа опалубки включаются инфракрасные электронагреватели. За счёт данного термопрогрева опалубки можно не использовать дорогостоящие, дополнительные процедуры, применяемые на ЖБИ-заводах: пар, паропровод, прогревочный провод. Всего 4 часа для подъёма температуры, 12 часов выдержки, 5-6 часов остывания (в общей сложности время изготовления занимает менее суток) и монолитная преднапряжённая балка готова
Благодаря скорости изготовления и отсутствию сложной доставки стоимость полученной преднапряжённой балки, включая затраты на изготовление опалубки, будет на 30% меньше стоимости стандартной балки с завода ЖБИ.
ОТЛИЧИТЕЛЬНЫЕ ОСОБЕННОСТИ ТЕХНОЛОГИИ ПСК-Строитель
· Конечная цена балки пролетного строения опалубки получается ниже заводской более чем на 30%
· Прогнозируемое качество изделия – гарантия прочности каждой производимой балки
· Простота монтажа опалубки (ГК ПСК предоставляет весь комплекс услуг супервайзинга), опалубка легко монтируется и демонтируется с помощью винтовых стяжек
· Балки не нуждаются в сложной транспортировке (никакого спецтранспорта!), так как формируются на строительной площадке. А разобранную опалубку свободно перевезут две обычные газели.
А разобранную опалубку свободно перевезут две обычные газели.
· Технология управляемого электрического прогрева опалубки может быть полностью автоматизирована с помощью компьютерных технологий. Оператор ПК в этом случае может удалённо управлять подачей температуры на разные секции балки с помощью датчиков температуры, выравнивая температуру по всей конструкции
· Опалубка предоставляется в аренду под конкретный проект (комплектуем в зависимости от конструкции балки)
· ГК ПСК оказывает полный спектр услуг по устройству систем преднапряжения: поставка материалов, выполнение строительно-монтажных работ, услуги по шеф-монтажу и предоставление в аренду оборудования.
Предварительно напряженные железобетонные конструкции: использование
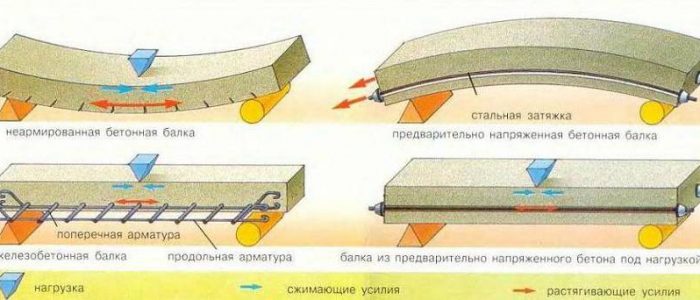
Железобетонные конструкции — основа современного строительства. Однако они имеют существенные изъяны, связанные, в первую очередь, с недостаточной нагрузочной способностью и образованием трещин в камне при эксплуатационных нагрузках. Усовершенствование технологии изготовления изделий из бетона и стальной арматуры привело к созданию преднапряженного железобетона, который обладает рядом преимуществ.
Однако они имеют существенные изъяны, связанные, в первую очередь, с недостаточной нагрузочной способностью и образованием трещин в камне при эксплуатационных нагрузках. Усовершенствование технологии изготовления изделий из бетона и стальной арматуры привело к созданию преднапряженного железобетона, который обладает рядом преимуществ.
Определение
Предварительно напряженные железобетонные конструкции — строительные изделия, бетон которых на этапе создания принудительно получает начальную расчетную напряженность сжатия. Она создается за счет предварительного формирования напряжения растяжения в рабочей высокопрочной арматуре и обжатия ею бетона на тех участках, которым предстоит испытывать растяжение (прогиб) при эксплуатации. Сжимаясь, арматура не проскальзывает, так как сцеплена с материалом или удерживается анкерным закреплением арматуры на торцах изделий. Таким образом, напряжение растяжения, которое приобретает железобетонный состав с помощью армирования, уравновешивает напряженность заблаговременного обжатия камня.
Вернуться к оглавлению
Преимущества
Предварительно напряженный железобетон долгосрочно отодвигает время начала формирования расколов в изделиях, работающих на прогиб, сокращает глубину их раскрывания. Вместе с тем изделия приобретают повышенную жесткость, не снижая прочности.
Предварительно напряженным железобетонным балкам свойственно хорошо работать на сжатие и прогиб, имея одинаковую прочность по длине, что позволяет увеличивать ширину перекрываемых пролетов. В таких конструкциях уменьшаются размеры поперечного сечения, следовательно, сокращаются объем и вес комплектующих элементов (на 20 – 30%), а также расход цемента. Более рациональное использование свойств стали позволяет сокращать расход арматуры (стержневой и проволочной) до 50%, особенно из высокопрочных марок (A-IV и выше), имеющих значительный предел прочности. Химическая нейтральность бетона к стали способствует предохранению арматуры от коррозии. Вместе с тем повышенная трещиностойкость предохраняет напряженную арматуру от ржавления в сооружениях, которые находятся под постоянным давлением воды, иных жидкостей, газов.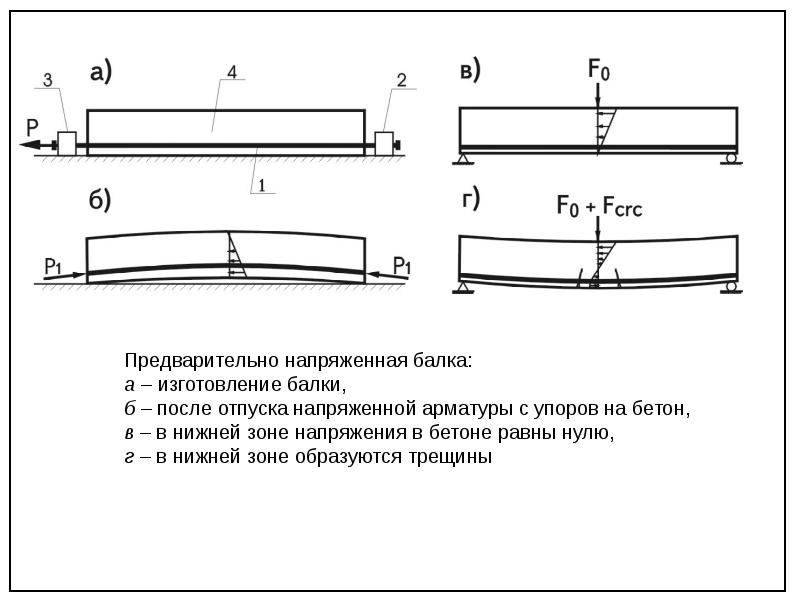
Методы возведения зданий, используемые в строительстве каркаса, базируются на технологии предварительного напряжения конструкций из железобетона в процессе строительства.
Напряженная арматура, обжимающая бетон сборочных единиц, обеспечивает практичную их стыковку путем значительного сокращения расходования металла на стыках. Сборные и сборно-монолитные изделия из железобетонных напряженных конструкций могут состоять из стыкуемых частей с одинаковым поперечным сечением, которые по краям выполняются из ненапряженных облегченных (тяжелых) бетонов, а нагружаемый фрагмент — преднапряженный железобетон. Такая продукция имеет повышенную выносливость, компенсируя повторяющиеся динамические воздействия.
Данное свойство позволяет демпфировать изменения напряжений в бетоне и арматуре, вызываемые колебаниями внешних нагрузок. Повышенная сейсмическая стойкость зданий повышается за счет большой конструкционной устойчивости напряженного железобетона, обжимающего отдельные их фрагменты. Конструкция в предварительно напряженном виде обеспечивает большую безопасность, так как ее разрушению предшествует запредельный прогиб, сигнализирующий об исчерпании конструкцией прочности.
Конструкция в предварительно напряженном виде обеспечивает большую безопасность, так как ее разрушению предшествует запредельный прогиб, сигнализирующий об исчерпании конструкцией прочности.
Вернуться к оглавлению
Недостатки
Состояние предварительного напряжения в материале достигается спецоборудованием, точными расчетами, трудоемким конструированием и затратным производством. Продукция требует бережного хранения, транспортировки и монтажа, которые не вызывают ее аварийного состояния еще до начала использования.
Сосредоточенные нагрузки могут способствовать возникновению продольных трещин, которые снижают несущую способность. Просчеты в проектировании и технологии производства могут вызывать полное разрушение создаваемого железобетонного изделия на стапеле. Предварительно напряженные конструкции требуют металлоемкой опалубки повышенной прочности, увеличенного расхода стали на закладные и арматуру.
Большие значения звуко– и теплопроводности требуют закладывания в тело камня компенсирующих материалов. Подобными железобетонными конструкциями обеспечивается более низкий порог огнестойкости (ввиду меньшей критической температуры нагрева преднапряженной арматурной стали) по сравнению с обычным железобетоном. На преднапряженную бетонную конструкцию критично воздействуют выщелачивание, растворы кислот и сульфатов, солей, приводящие к коррозии цементного камня, раскрытию трещин и коррозии арматуры. Это может приводить к резкому снижению несущей способности стали и внезапному хрупкому разрушению. Также к минусам стоит отнести значительный вес изделий.
Подобными железобетонными конструкциями обеспечивается более низкий порог огнестойкости (ввиду меньшей критической температуры нагрева преднапряженной арматурной стали) по сравнению с обычным железобетоном. На преднапряженную бетонную конструкцию критично воздействуют выщелачивание, растворы кислот и сульфатов, солей, приводящие к коррозии цементного камня, раскрытию трещин и коррозии арматуры. Это может приводить к резкому снижению несущей способности стали и внезапному хрупкому разрушению. Также к минусам стоит отнести значительный вес изделий.
Вернуться к оглавлению
Материалы для конструкций
Железобетон — многокомпонентный материал, основными составляющими которого являются бетон и стальная арматура. Параметры их качества определяются особыми требованиями при проектировании к элементам конструкций на месте применения.
Вернуться к оглавлению
Бетон
Формы для заливки бетона с прутьями для передачи предварительного напряжения.
Предварительное напряжение в железобетоне обеспечивается применением тяжелых составов средней плотности от 2200 до 2500 кг/м3, которые имеют классы по прочности на осевое растяжение выше Bt0,8, по прочности от В20 и больше, марки по водонепроницаемости от W2 и выше, по морозостойкости от F50. Требования к продукции гарантируют бетону нормативную прочность не ниже установленной с вероятностью 0,95 (в 95% случаев). Смесь должна набрать возраст не меньше 28 суток до получения материалом предварительных напряжений. На ранних стадиях эксплуатации бетонный камень способен частично утерять напряженное качество за счет общего снижения напряженности стали (до 16%). Коэффициент надежности материала на растяжение и сжатие в предельных состояниях установлен для эксплуатационной пригодности не ниже 1,0.
Требования к продукции гарантируют бетону нормативную прочность не ниже установленной с вероятностью 0,95 (в 95% случаев). Смесь должна набрать возраст не меньше 28 суток до получения материалом предварительных напряжений. На ранних стадиях эксплуатации бетонный камень способен частично утерять напряженное качество за счет общего снижения напряженности стали (до 16%). Коэффициент надежности материала на растяжение и сжатие в предельных состояниях установлен для эксплуатационной пригодности не ниже 1,0.
Вернуться к оглавлению
Арматура
Стальная начинка должна оставаться напряженной в железобетонном изделии на всем интервале эксплуатации, выдерживая без вытяжения длительно приложенные нагрузки. В преднапряженных изделиях из железобетона используется высокопрочная сталь с незначительной текучестью, соответствующей параметрам ползучести бетона.
С целью компенсирования эксплуатационной потери некоторой величины преднапряжения при изготовлении ее значение устанавливают чуть выше, чем предусмотрено строительными требованиями для конструкционного элемента. В продукции применяют горячекатаную упрочненную, холоднодеформированную арматуру, арматурную проволоку (пучки, пакеты, пряди), канаты, сварные каркасы и пр. Поперечное сечение арматуры может быть гладким, периодическим, а укладка проволоки и канатов серповидной и кольцевой.
В продукции применяют горячекатаную упрочненную, холоднодеформированную арматуру, арматурную проволоку (пучки, пакеты, пряди), канаты, сварные каркасы и пр. Поперечное сечение арматуры может быть гладким, периодическим, а укладка проволоки и канатов серповидной и кольцевой.
Сталь должна гарантированно соответствовать установленному классу относительно прочности по преднапряженному растяжению (текучесть металла должна находиться в пределах 0,2% относительного удлинения) с вероятностью от 0,95 и выше. Арматуре необходимо быть пластичной, хладостойкой, свариваемой и пр. Надежное сцепление с бетонной смесью обеспечивается формированием арматурой сложных пространственных поверхностей.
Вернуться к оглавлению
Области использования конструкций
Предварительно напряженный бетон позволяет сократить до 50% расхода арматурной стали.
Преднапряженные изделия используются, когда применение обычного железобетона нецелесообразно (перерасход материалов, рост веса и стоимости, невозможность обеспечить несущую прочность и пр.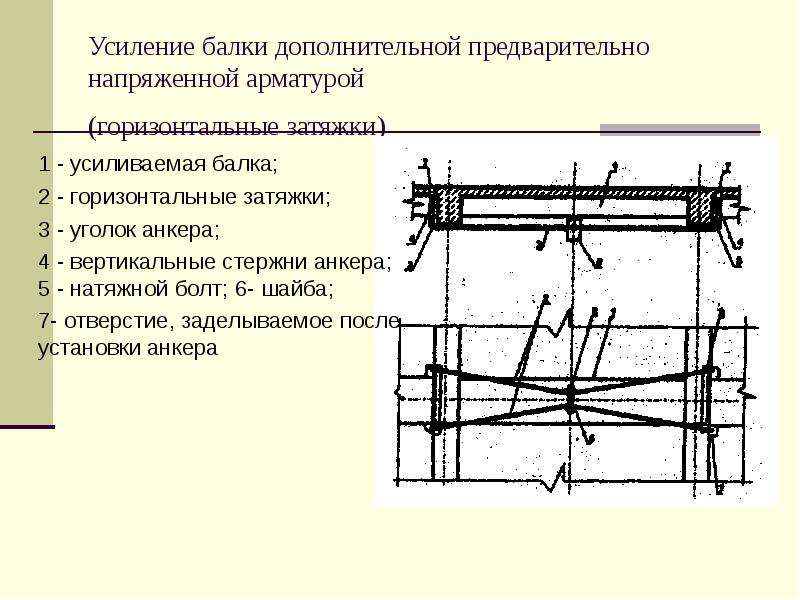 ). Сферами их использования являются гражданское, промышленное, специальное и гидротехническое строительство. Объекты — каркасы и мосты с широкими пролетами, напорные трубопроводы, плотины, водонепроницаемые емкости и пр.
). Сферами их использования являются гражданское, промышленное, специальное и гидротехническое строительство. Объекты — каркасы и мосты с широкими пролетами, напорные трубопроводы, плотины, водонепроницаемые емкости и пр.
А также из них создают подпорные стены, ограждающие панели, лестничные марши, подкрановые балки, фундаменты, колонны, столбы ЛЭП, каркасы тоннелей, междуэтажные перекрытия и пр. Такая продукция незаменима и при возведении построек в условиях взрыво- и сейсмоопасности. Особенно эффективна она при формировании сборно-монолитных конструкций, когда отдельные преднапряженные сборные элементы соединяются в проектном положении арматурой так, что работают как одно целое.
Вернуться к оглавлению
Вывод
Преднапряженные изделия из железобетона имеют много достоинств. Их недостатки могут быть нивелированы качеством проектирования, производства и монтирования, способствующим длительной эксплуатации.
Расчет балки из предварительно–напряженного железобетона — Студопедия
Расчёт на прочность по изгибающему моменту.
Расчёту подлежат балочные пролётные строения железнодорожных мостов из предварительно напряжённого железобетона (типовой проект серии 3.501-81).
Действительную форму поперечного сечения приводим к расчётной форме (рис. 7).
Действительная форма плиты переменной толщины и вутов заменяется в расчётном сечении прямоугольной формой с толщиной hф’ и шириной bф’.
Рис. 7. Расчётная схема поперечного сечения главной балки.
Вычисляем приведённую (среднюю) толщину плиты при фактической ширине плиты bп=2,09 м:
Расчётная ширина не должна превышать расстояния между осями B=1,8м.
Поэтому принимаем
Центр тяжести арматуры ориентировочно назначается на расстоянии as=0,15 м от нижней грани пояса балки.
Расчёт на прочность по изгибающему моменту производим, начиная с наиболее нагруженного сечения. Определим в первом приближении высоту сжатой зоны бетона x1 при действии расчётного момента M2:
Так как x1=0,242м >hп’=0,22 м, то в сжатую зону, кроме плиты, входит часть ребра главной балки, и сечение рассчитывается как тавровое. Расчётный изгибающий момент М2 можно представить как сумму двух моментов: М2’-воспринимаемый свесами плиты, М2’’— воспринимаемый сжатой зоной ребра:
Расчётный изгибающий момент М2 можно представить как сумму двух моментов: М2’-воспринимаемый свесами плиты, М2’’— воспринимаемый сжатой зоной ребра:
Определим предельный момент, воспринимаемый свесами плиты и соответствующей частью рабочей арматуры:
По оставшейся зоне находим высоту сжатой зоны ребра:
Плечо пары внутренних сил таврового сечения:
Определяем в первом приближении необходимую площадь рабочей арматуры:
Задаваясь диаметром высокопрочной проволоки B-II равным 6мм, определяем общее количество пучков
После уточнения площади с учётом принятого диаметра и количества стержней арматуры находим значение :
Вычисляем окончательное значение плеча пары внутренних сил:
Условие прочности сечения по изгибающему моменту записывается в виде:
(11317. 058>10680.265) кН∙м
058>10680.265) кН∙м
Проверка выполняется.
Расположение рабочей арматуры представлено на рис. 8.
Рис.8. Расположение рабочей арматуры.
Расчет на трещеностойкость в стадии изготовления и эксплуатации.
А. Проверка против образования нормальных трещин в стадии эксплуатации.
Расчет производится по наибольшему изгибающему моменту от нормативных нагрузок. Предполагается, что на стадии образования трещин бетон и арматура сохраняют упругие свойства. Благодаря предварительному напряжению конструкция работает полным сечением.
После размещения рабочей арматуры определяем размеры нижнего пояса балки.
Существует 2 способа создания предварительного напряжения:
-на упоры;
-на бетон;
Так как главные балки будут изготавливаться в заводских условиях, то мы будем рассматривать 1ый способ.
При напряжении арматуры на упорыеё сцепление с бетоном обеспечивается до передачи усилия предварительного натяжения на конструкцию. На всех стадиях изготовления и эксплуатации бетон и арматура в сечениях работают совместно. Для таких конструкций определяются геометрические характеристики только приведённого сечения.
На всех стадиях изготовления и эксплуатации бетон и арматура в сечениях работают совместно. Для таких конструкций определяются геометрические характеристики только приведённого сечения.
Определяем геометрические характеристики бетонного сечения. Нейтральная ось сечения расположена от нижней грани балки на расстоянии:
Площадь бетонного сечения:
Статический момент бетонного сечения относительно нижней грани балки:
Площадь приведенного сечения вычисляется по формуле:
Для бетона класса B30 коэффициент приведения напрягаемой арматуры к бетону берётся равный 5,4.
Статический момент приведенного сечения относительно нижней грани балки:
Момент инерции приведенного сечения относительно нейтральной оси вычисляется по формуле:
Допустимые в период эксплуатации предельные растягивающие напряжения в бетоне для ж\д мостов- . Исходя из этого определяем усилие натяжения арматуры N, передаваемое на бетон конструкции:
Исходя из этого определяем усилие натяжения арматуры N, передаваемое на бетон конструкции:
растягивающие напряжения в бетоне;
ожидаемые растягивающие напряжения у нижней грани:
Установившиеся напряжения в арматуре от ее предварительного натяжения:
Напряжения σр2 при натяжении арматуры должны быть увеличены с учетом неизбежных потерь напряжений с течением времени от усадки и ползучести бетона, релаксации арматуры и влияния других факторов.
Проверка выполняется.
Б. Проверка трещиностойкости балки в стадии изготовления.
В стадии изготовления на конструкцию действуют сила предварительного напряжения и собственный вес балки. На этой стадии проверяем в середине пролета сжимающие нормальные напряжения в крайнем волокне нижнего пояса. Для конструкции с натяжением арматуры на упоры имеем:
На этой стадии проверяем в середине пролета сжимающие нормальные напряжения в крайнем волокне нижнего пояса. Для конструкции с натяжением арматуры на упоры имеем:
Момент собственного веса балки в середине пролета определяется по формуле:
(-14861.102<16700)кПа
Проверка выполняется.
При создании предварительного напряжения в верхней зоне балки могут возникнуть растягивающие напряжения, величина которых для конструкций с натяжением арматуры на бетон определяется по формуле:
(1010.918<1440)кПа
Проверка выполняется.
Для конструкций с натяжением арматуры на упоры, как и в предыдущем случае, в формулу подставляют геометрические характеристики приведенного сечения.
Расчет на трещеностойкость по касательным и главным напряжениям
Расчет производится в стадии эксплуатации на усилия и от нормативных нагрузок и воздействие силы предварительного напряжения N. Предполагается, что в стадии эксплуатации конструкция работает упруго и полным сечением. Напряжения определяются в трех точках по высоте сечения: в местах примыкания плиты и нижнего пояса к стенке балки и на нейтральной оси. Выполняя курсовой проект, ограничиваемся проверкой касательных и главных напряжений в сечениях у опоры и в середине пролета.
Предполагается, что в стадии эксплуатации конструкция работает упруго и полным сечением. Напряжения определяются в трех точках по высоте сечения: в местах примыкания плиты и нижнего пояса к стенке балки и на нейтральной оси. Выполняя курсовой проект, ограничиваемся проверкой касательных и главных напряжений в сечениях у опоры и в середине пролета.
А. Проверка касательных напряжений.
Касательные напряжения определяются по формуле
— статический момент части сечения, расположенной выше (или ниже) точки, в которой определяются касательные напряжения, относительно нейтральной
оси приведенного сечения.
Пучки рабочей арматуры отклоняются для уменьшения действующей поперечной силы.
Отклоняют пучки на расстоянии 1/3 длины балки от опоры, но не ближе ¼ длины, располагая их равномерно по высоте стенки в опорном сечении (см. рис.9).
Рис.9. Схема расположения отклонённых пучков в предварительно-напряжённой балке.
Поперечная сила в сечении, создаваемая отклоненными пучками предварительно-напряжённой арматуры равна:
Касательные напряжения определяются в 2ух сечениях(в середине пролёта и в месте изменения толщины ребра) в трёх точках по высоте сечения: в местах примыкания плиты и нижнего пояса к стенке и на нейтральной оси (см рис. 10).
10).
Рис.10. Схема к расчёту предварительно-напряжённой балки на поперечную силу.
В середине пролёта (сечение б-б):
Проверки выполняются.
В месте изменения толщины ребра (сечение а-а):
Проверки выполняются.
По касательным напряжениям на нейтральной оси проверяется принятая толщина стенки балки. Вычисленные значения касательных напряжений используются при определении главных напряжений.
Б. Проверка главных напряжений.
Вычисляются главные растягивающие и главные сжимающие напряжения по формуле:
Нормальные напряжения определяются от действия силы предварительного напряжения и изгибающего момента от эксплутационных нагрузок:
у – имеет положительное значение выше нейтральной оси, отрицательное – ниже нейтральной оси.
Так как балка не армируется напряжёнными хомутами, то = 0
Главные напряжения недолжны превышать предельных значений:
-главные сжимающие напряжения ;
-главные растягивающие напряжения не более значений приведенных в таблице ниже.
Промежуточные значения принимаются по интерполяции.
В середине пролета (сечение б-б):
Точка 1:
Точка 2:
Точка 3:
Проверки выполняются.
В месте изменения толщины ребра (сечение а-а):
Точка 1:
Точка 2:
Точка 3:
Проверки выполняются.
Расчет на прочность по поперечной силе
Расчет производится в сечении, образованном наклонной трещиной. Поперечная сила воспринимается отклоненными пучками напряженной арматуры, хомутами и бетоном сжатой зоны сечения (см. рис.11).
Рис.11. Схема к расчёту предварительно напряжённой балки на поперечную силу.
Определяем распределенную поперечную нагрузку, воспринимаемую хомутами в наклонном сечении:
и — проекция усилий в отклоненных пучках и бетоне сжатой зоны сечения на вертикальную ось.
— расчетное сопротивление отклоненных пучков.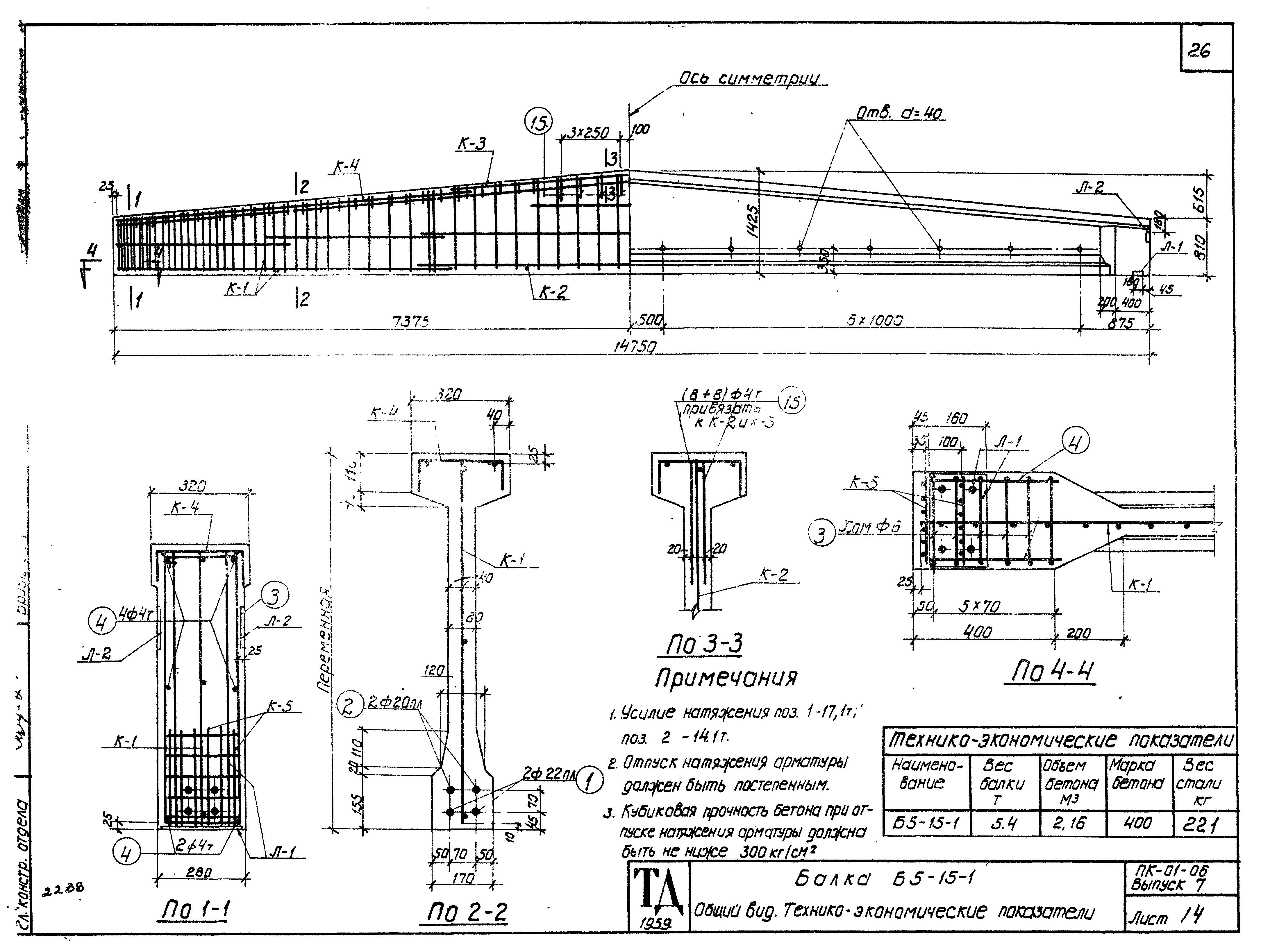
с – длина горизонтальной проекции наклонного сечения, определяемая из условия, что угол наклона сечения к продольной оси балки составляет 30 градусов.
Прочность хомутов обеспечивается при выполнении условия:
где и — предельные усилия на единицу длины в обычных и
напряженных хомутах.
и — расчетные сопротивления обычных и напряженных хомутов.
При отсутствии напряженных хомутов в балке, в данной формуле qрω принимается равным нулю.
Диаметр обычных хомутов назначаем 8мм A-III, а на концевых участках 10мм A-III. Шаг хомутов принимаем: на концевых участках с длиной равной высоте балки, 10см; на приопорных участках до четверти длины пролёта-15см; на среднем участке-20см.
Проверка выполняется.
Нижний пояс предварительно-напряженной балки армируется замкнутыми хомутами того же диаметра, что и хомуты стенки.
Справочник проектировщика промышленных, жилых и общественных зданий и сооружений. Расчетно-теоретический. 1960 г. Уманский А.А.
Расчетно-теоретический. 1960 г. Уманский А.А.
РАЗДЕЛ 1. МАТЕМАТИКА. Чл.-корр. АН УССР д-р физ.-мат. наук проф. И. Я. Штаерман 19
1.1. Алгебра 19
1.1.1. Степени и корни 19
1.1.2. Логарифмы 19
1.1.3. Прогрессии 20
1.1.4. Факториал 20
1.1.5. Соединения 20
1.1.6. Бином Ньютона 20
1.1.7. Определители (детерминанты) 20
1.1.8. Линейные уравнения 21
1.1.9. Матрицы (канд. техн. наук В. В. Новицкий) 22
1.1.10. Уравнения высших степеней 23
1.1.11. Приближенное решение уравнений 24
1.2. Геометрия 25
1.2.1. Плоские фигуры. Многоугольники .Круг и его части. Площади, ограниченные кривыми второго порядка 25
1.2.2. Тела. Тела, ограниченные плоскостями. Цилиндр и конус. Шар и его части. Некоторые другие тела. Тела вращения (теоремы Гюльдена). Призматоид. Рампа 26
1.3. Тригонометрия 27
1.3.1. Измерение углов 27
1. 3.2. Тригонометрические (круговые) функции . . 27
3.2. Тригонометрические (круговые) функции . . 27
1.3.3. Функции суммы и разности углов, кратных углов и половинного угла 29
1.3.4. Степени функций 29
1.3.5. Приведение к виду, удобному для логарифмирования 29
1.3.6. Зависимости между функциями трех углов, сумма которых равна 180° 29
1.3.7. Зависимости между обратными тригонометрическими функциями 30
1.3.8. Формулы, применяемые при решении треугольников 30
1.3.9. Гиперболические функции 31
1.4. Аналитическая геометрия 31
1.4.1. Точка на плоскости 31
1.4.2. Прямая линия 32
1.4.3. Окружность 32
1.4.4 Парабола 32
1.4.5. Эллипс и гипербола 33
1.4.6. Построение конических сечений 34
1.4.7. Цепная линия. Циклоида. Спираль 34
1.4.8. Точка в пространстве 34
1.4.9. Плоскость 35
1.4.10. Прямая в пространстве 35
1.4.11. Поверхности второго порядка 35
1. 5. Дифференциальная геометрия 36
5. Дифференциальная геометрия 36
1.5.1. Плоские кривые 36
1.5.2. Пространственные кривые 38
1.5.3. Поверхности 39
1.6. Дифференциальное исчисление 39
1.6.1. Функция, предел, непрерывность 39
1.6.2. Производная и дифференциал 40
1.6.3. Раскрытие неопределенностей 41
1.6.4. Исследование функций 41
1.6.5. Функция двух переменных 41
1.7. Интегральное исчисление 42
1.7.1. Неопределенный интеграл 42
1.7.2. Интегрирование рациональных функций 43
1.7.3. Интегрирование иррациональных функций 44
1.7.4. Интегрирование трансцендентных функций 44
1.7.5. Определенный интеграл 46
1.7.6. Кратные интегралы 47
1.7.7. Криволинейные интегралы 48
1.8. Ряды 48
1.8.1. Числовые ряды 48
1.8.2. Степенные ряды 49
1.9. Дифференциальные уравнения 51
1.9.1. Основные понятия 51
1. 9.2. Уравнения первого порядка 51
9.2. Уравнения первого порядка 51
1.9.3. Уравнения второго порядка 51
1.9.4. Линейные уравнения второго порядка 52
1.9.5. Линейные уравнения высших порядков с постоянными коэффициентами 53
1.9.6. Метод начальных параметров 53
1.9.7. Общие решения дифференциального уравнения четвертого порядка с биквадратным характеристическим уравнением (канд. техн. наук А. И. Тюленев) 54
1.9.8. Приближенные методы 54
1.9.9. Уравнения математической физики 58
1.9.10. Квазилинейные уравнения 59
1.10. Функции комплексной переменной 60
1.10.1. Комплексные числа 60
1.10.2. Комплексные функции 60
1.10.3. Конформные отображения 61
1.11. Вариационное исчисление 61
1.11.1. Постановка задачи 61
1.11.2. Основные случаи 62
1.11.3. Прямые методы 63
1.12. Разностное исчисление 63
1.12.1 Определение разностей 63
1. 12.2. Разностные уравнения 63
12.2. Разностные уравнения 63
1.13. Интегральные уравнения 64
1.13.1. Уравнения Фредгольма. Методы решения однородного уравнения. Методы решения неоднородного уравнения 64
1.13.2. Уравнения Вольтерра второго рода 65
1.13.3. Уравнения Абеля 65
1.13.4. Сингулярные уравнения 65
1.14. Специальные функции 66
1.14.1. Полиномы Лежандра 66
1.14.2. Полиномы Чебышева 66
1.14.3. Гамма-функция 66
1.14.4 Функции Бесселя 66
1.15. Операционное исчисление 67
1.15.1. Преобразование Лапласа 67
1.15.2. Применение операционного исчисления 68
1.16. Векторное и тензорное исчисления 68
1.16.1. Векторная алгебра 68
1.16.2. Векторный анализ 69
1.16.3. Тензоры 69
1.17. Приближенные вычисления 70
1.17.1. Общие положения 70
1.17.2. Приближенные формулы 71
1.18. Номография 71
1. 18.1. Функциональная шкала 71
18.1. Функциональная шкала 71
1.18.2. Номограммы из выравненных точек 71
1.18.3. Сетчатые номограммы 72
1.18.4. Номограммы для уравнений с числом переменных более трех 72
1.19. Приближенное представление функций 72
1.19.1. Постановка задачи 72
1.19.2. Интерполяционные формулы 72
1.19.3. Приближение функций по методу наименьших квадратов 74
1.19.4. Приближенное вычисление определенных интегралов 75
1.20. Ряды Фурье 76
1.20.1. Разложение функций в ряд Фурье 76
1.20.2. Интеграл Фурье 79
1.20.3. Приближенный гармонический анализ 80
1.21. Теория вероятностей 81
1.21.1. Понятие вероятности 81
1.21.2. Случайные величины 82
1.21.3. Обработка наблюдений 82
1.21.4. Основы теории корреляции 83
1.22. Математические таблицы 84
1.22.1. Степени, корни, натуральные логарифмы 84
1. 22.2. Тригонометрические функции. Синусы и косинусы 92
22.2. Тригонометрические функции. Синусы и косинусы 92
1.22.3 Круговые, показательные и гиперболические функции 94
1.22.4. Некоторые постоянные 97
1.22.5. Соотношение между английскими и метрическими мерами 97
РАЗДЕЛ 2. ТЕОРЕТИЧЕСКАЯ МЕХАНИКА. Д-р техн. наук проф. А. Н. Обморшев. 99
СТАТИКА 99
2.1. Геометрическая статика 99
2.1.1. Основные положения 99
2.1.2. Сложение и разложение сил 100
2.1.3. Моменты сил и пар 100
2.1.4. Параллельные силы 101
2.1.5. Произвольная система сил 101
2.1.6. Правила прикрепления твердого тела 104
2.1.7. Системы с трением 104
2.1.8. Центр тяжести 105
2.2. Графостатика 106
2.2.1. Веревочный многоугольник 106
2.2.2. Применение веревочного многоугольника к определению опорных реакций 108
2.2.3. Определение усилий в стержнях плоских статически определимых ферм 109
2. 2.4. Разложение силы по трем прямым, пересекающимся в одной точке и не лежащим в одной плоскости 110
2.4. Разложение силы по трем прямым, пересекающимся в одной точке и не лежащим в одной плоскости 110
2.2.5. Разложение силы по шести произвольно расположенным прямым 110
2.3. Аналитическая статика 111
2.3.1. Работа. Мощность 111
2.3.2 Потенциальная энергия 112
2.3.3. Принцип возможных перемещений 113
КИНЕМАТИКА 113
2.4. Кинематика точки 113
2.4.1 Прямолинейное движение точки 113
2.4.2. Криволинейное движение точки 114
2.4.3. Относительное движение точки 115
2.5. Кинематика твердого тела 115
2.5.1. Поступательное движение 115
2.5.2. Вращение вокруг неподвижной оси 115
2.5.3. Винтовое движение 116
2.5.4. Плоско-параллельное движение 116
2.5.5. Движение тела около неподвижной точки 117
2.5.6. Сложение скоростей или бесконечно малых перемещений при сложном движении твердого тела. Статико-кинематическая аналогия 117
Статико-кинематическая аналогия 117
2.5.7. Элементы кинематики механизмов 118
2.5.8. Кинематические пары, входящие в расчетные схемы сооружений 118
ДИНАМИКА 120
2.6. Механические единицы 120
2.6.1. Правило размерностей 120
2.7. Динамика точки 121
2.7.1. Основные законы 121
2.7.2. Прямолинейное движение точки 121
2.7.3. Криволинейное движение точки 122
2.7.4. Кинетостатика точки. Относительное движение 122
2.8. Динамика системы 122
2.8.1. Общие теоремы динамики 122
2.8.2. Общие принципы динамики системы 123
2.8.3. Моменты инерции 124
2.9. Динамика твердого тела 125
2.9.1. Вращение тела вокруг неподвижной оси 125
2.9.2. Физический маятник 125
2.9.3. Давление вращающегося тела на опоры 126
2.9.4. Плоско-параллельное движение 126
2.10. Удар 126
2. 10.1. Основные положения 126
10.1. Основные положения 126
2.10.2. Удар двух тел 126
2.10.3. Действие удара на вращающееся твердое тело 127
РАЗДЕЛ 3. НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ. Д-р техн. наук И. И. Трапезин 129
3.1. Напряжения 129
3.1.1. Основные понятия 129
3.1.2. Одноосное напряженное состояние 129
3.1.3. Плоское напряженное состояние 130
3.1.4. Объемное напряженное состояние 130
3.1.5. Преобразование компонентов напряжения к новым осям координат 132
3.1.6. Интенсивность напряжений в данной точке 132
3.1.7. Круги Мора 133
3.2. Деформации 134
3.2.1. Компоненты деформаций 134
3.2.2. Определение угловой деформации и величин главных удлинений по удлинениям в трех направлениях в случае плоской деформации и плоского напряженного состояния 135
3.2.3. Интенсивность деформаций 135
3.3. Зависимости между напряжениями и деформациями в пределах упругости 136
3. 3.1. Закон Гука для изотропного тела 136
3.1. Закон Гука для изотропного тела 136
3.3.2. Закон Гука для анизотропного тела 137
3.3.3. Плоскость симметрии в отношении упругих свойств 137
3.3.4. Ортотропное упругое тело 137
3.3.5. Потенциальная энергия упругого тела 138
3.4. Связь между напряжениями и деформациями за пределами упругости 138
3.4.1 Условия пластичности 138
3.4.2 Напряжения и деформации при простом нагружении и при разгрузке 138
3.4.3 Диаграммы растяжения 139
3.4.4 Схематизация истинных диаграмм растяжения 139
3.4.5. Построение кривой зависимости 140
РАЗДЕЛ 4. ПРОЧНОСТЬ МАТЕРИАЛОВ И МЕТОДЫ РАСЧЕТА КОНСТРУКЦИЙ. Кандидаты техн. наук доценты А. И. Коданев, В. Г.Чернашкин, Б. А. Дзержкович, чл.-корр. АСиА СССР канд. техн. наук С. А. Семенцов, канд. техн. наук Л. Н. Пицкель, д-р техн. наук проф. В. Н. Быковский, д-р техн. наук А. Б. Губенко, кандидаты техн. наук А. Г. Иммерман, Л В. Клепиков, В. А. Отставнов 141
А. Отставнов 141
4.1. Прочность материалов (А. И. Коданев) 141
4.1.1. Упругость, пластичность и разрушение 141
4.1.2. Влияние характера напряженного состояния 141
4.1.3. Влияние температуры 144
4.1.4. Влияние длительности нагружения 144
4.1.5. Влияние переменности нагрузки 145
4.1.6. Влияние концентрации напряжений 147
4.1.7. Влияние скорости приложения нагрузки 147
4.2. Строительные стали (В. Г. Чернашкин) 148
4.2.1. Основные понятия и обозначения 148
4.2.2. Физические свойства углеродистой стали 148
4.2.3. Химический состав и механические свойства углеродистой стали. Сталь углеродистая горячекатаная обыкновенного качества пс ГОСТ 380-50. Сталь углеродистая для мостостроения. Сталь углеродистая для армирования железобетонных конструкций 149
4.2.4. Химический состав и механические свойства низколегированной стали. Сталь низколегированная 10ХНДП (СХЛФ) с повышенным содержанием фосфора.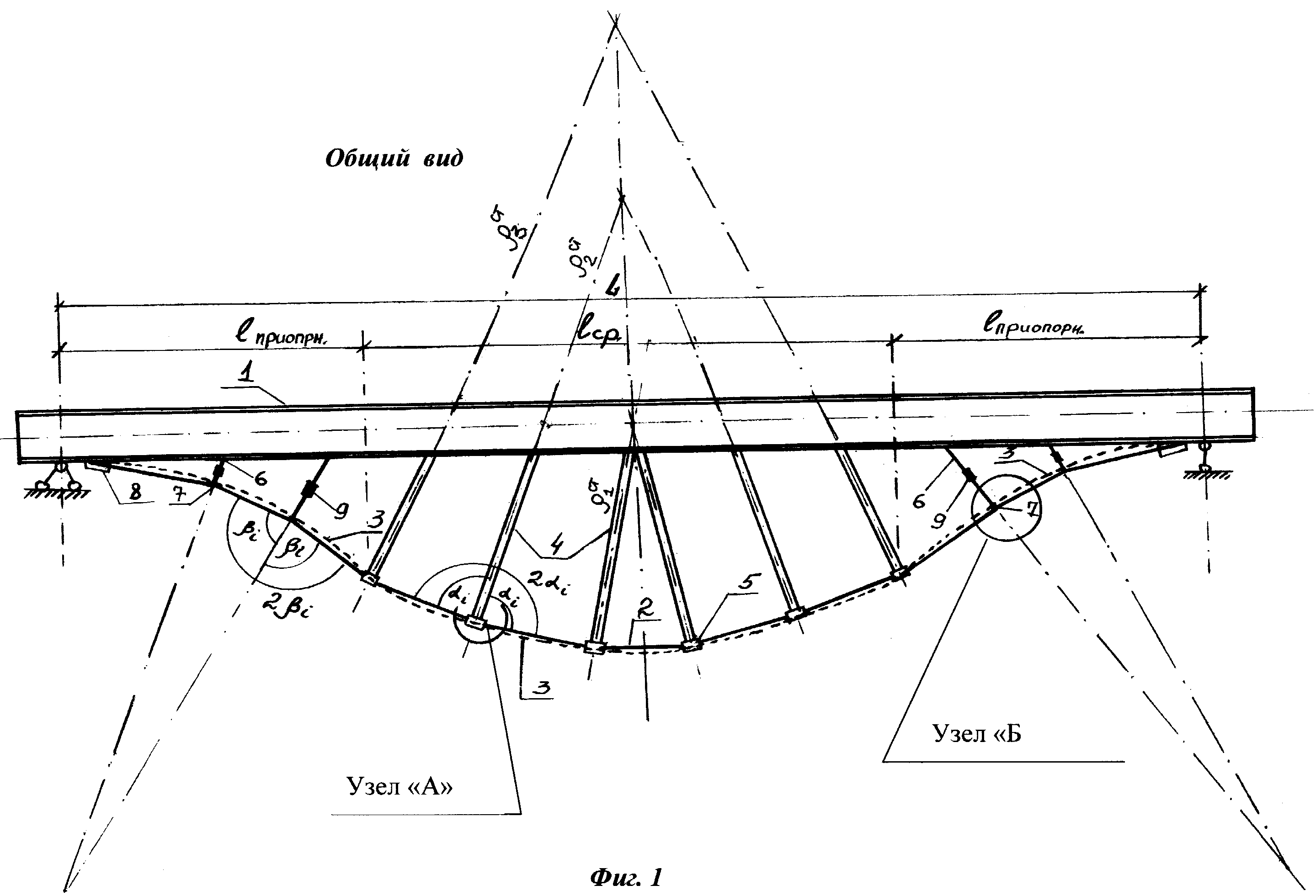 Сталь низколегированная марки 10Г2СД (МК). Сталь низколегированная марок 14ХГС и 19Г. Сталь низколегированная марки 15ГС 156
Сталь низколегированная марки 10Г2СД (МК). Сталь низколегированная марок 14ХГС и 19Г. Сталь низколегированная марки 15ГС 156
4.3. Сплавы алюминия для строительства(Б. А. Дзержкович) 162
4.4. Бетон (С. А. Семенцов) 164
4.4.1. Прочность 164
4.4.2 Деформация 166
4.5. Каменные материалы (С. А. Семенцов) 171
4.5.1. Прочность 171
4.5.2 Деформации 173
4.6. Армированные материалы (Л. Н. Пицкель) 174
4.6.1. Общие сведения 174
4.6.2. Железобетон 175
4.6.3. Армоцемент 179
4.6.4. Армированные каменные конструкции 179
4.6.5. Армированный асбестоцемент 180
4.7. Древесина (В. Н. Быковский) 181
4.7.1. Общие сведения 181
4.7.2. Механические свойства 181
4.8 Пластмассы в строительных конструкциях (А. Б. Губенко) 183
4.8.1. Конструктивные пластмассы 183
4.8.2. Конструкции с применением пластмасс 185
4. 8.3. Клеи и склеивание конструкций с применением пластмасс 186
8.3. Клеи и склеивание конструкций с применением пластмасс 186
4.9 Методы расчета конструкций 186
4.9.1. Метод расчета по расчетным предельным состояниям (Л. В. Клепиков, В. А. Отставнов) 186
4.9.2. Метод расчета по разрушающим нагрузкам (А. Г. Иммерман) 191
4.9.3. Метод расчета по допускаемым напряжениям (А. Г. Иммерман) 192
РАЗДЕЛ 5. СТРОИТЕЛЬНАЯ МЕХАНИКА БРУСА И СИСТЕМ БРУСЬЕВ. Д-р техн. наук проф. А. А. Уманский 195
5.1. Основные положения технической теории бруса 195
5.1.1. Определения 195
5.1.2. Основные факторы работы бруса. Статико-кинематическая аналогия. Нагрузки и усилия. Деформации и перемещения. Статико-кинематическая аналогия 195
5.1.3. Интегральные соотношения между напряжениями и усилиями в поперечных сечениях 197
5.1.4. Соответствующие силы и перемещения, усилия и дислокации 197
5.1.5. Начальная, температурная и упругая распределенные деформации 199
5.1.6. Две системы координатных осей упругого бруса с несимметричным сечением 200
5.1.7. Упругое основание 200
5.1.8. Плоский неразветвленный упругий брус. Обобщенная статико-кинематическая аналогия 200
5.2. Определение нормальных напряжений 202
5.2.1. Геометрические характеристики поперечных сечений брусьев 202
5.2.2. Определение моментов инерции относительно исходных осей 203
5.2.3. Редуцирование площадей при вычислении моментов инерции 203
5.2.4. Общая формула нормального напряжения при растяжении-сжатии и изгибе. Нейтральная линия 205
5.2.5. Максимальные нормальные напряжения 206
5.2.6. Ядро сечения 206
5.2.7. Случай переменного модуля Е 207
5.2.8. Пользование центральными неглавными осями 207
5.3. Определение касательных напряжений и деформаций в брусьях. Особенности тонкостенных сечений 208
5.3.1. Расчет на срез (сдвиг) 208
5.3.2. Расчет на направленный срез (сдвиг). Формулы для погонных касательных усилий и напряжений 208
5.3.3. Касательные напряжения при изгибе. Центр изгиба 210
5.3.4. Деформация сдвига при изгибе брусьев с массивным сечением и двутавровых балок 212
5.3.5. Касательные напряжения при изгибе и центр изгиба открытых тонкостенных сечений 212
5.3.6. Касательные напряжения при изгибе и центр изгиба замкнутых тонкостенных сечений 215
5.3.7. Касательные напряжения и относительный угол закручивания при свободном кручении. Геометрические характеристики 217
5.3.8. Депланация при свободном кручении. Эпюры единичной депланаций при свободном кручении для тонкостенных сечений 219
5.3.9. Стесненное кручение 219
5.3.10. Сложное сопротивление тонкостенных брусьев. Приведение нагрузок к типам усилий 221
5.4. Классификация систем брусьев и общие методы строительной механики 222
5.4.1. Основные определения 222
5.4.2. Виды систем Балки. Арки. Рамы. Фермы. Комбинированные системы. Спаренные плоские системы (биконструкции) 223
5.4.3. Статический метод определения перемещений и кинематический метод определения усилий на примере балки. Инфлюенты (линии и поверхности влияния). Статический метод определения перемещения в статически определимой системе. Кинематический метод определения усилия в статически определимой системе. Обобщенная теорема о взаимности работ активных факторов, действующих на упругую систему. Формулы для перемещения в упругой с. н. системе. Формулы для усилия в с. н. системе. Теоремы о взаимности единичных перемещений и усилий 226
5.4.4 Метод потенциальной энергии. Выражение энергии деформации через обобщенные силы и обобщенные перемещения. Выражение энергии деформации через силы и единичные перемещения. Выражение энергии деформации системы брусьев через усилия. Теорема Кастильяно. Теорема о минимуме энергии деформации. Случай заданных (температурных или начальных) деформаций. Выражение энергии деформации через перемещения или дислокации. Теорема об экстремуме полной энергии. Случай нелинейно-деформируемой системы, когда энергия деформации не есть функция второй степени от нагрузок 229
5.5. Балки 231
5.5.1. Определение усилий и перемещений и построение эпюр в балках по методу начальных параметров. Общие положения. Обыкновенная балка постоянного сечения. Обыкновенная балка переменного сечения . «Графоаналитический» метод определения перемещений в обыкновенных балках. Концевые углы поворота сечений простой балки как фиктивные реакции 231
5.5.2. Абсолютно жесткая балка на упругом основании и обыкновенная балка с защемленными концами. Уравнения эпюр. Абсолютно жесткие балки со свободными концами на упругом основании. Обыкновенные балки с защемленными концами 238
5.5.3. Приемы, упрощающие построение эпюр и инфлюент статически определимых балок 240
5.5.4. Равнопролетные неразрезные балки на жестких опорах. Метод бесконечной основной системы. Полубесконечная балка. Бесконечная балка. Построение инфлюент. Конечная равнопролетная балка 241
5.5.5. Равнопролетные неразрезные балки постоянного сечения на упруго оседающих опорах. Метод начальных параметров. Бесконечная и полубесконечная балки. Расчет конечных равнопролетных балок по таблицам для бесконечных балок 243
5.5.6. Балка на упругом (винклеровском) основании. Общие данные. Уравнения эпюр. Однопролетная балка. Бесконечная двусторонняя балка. Полубесконечная балка. Использование бесконечной балки для расчета конечных балок (Метод компенсирующих нагрузок). Практические указания. Дополнительная литература 248
5.5.7. Общий метод расчета неразрезных балок на жестких опорах. Уравнение трех опорных моментов 253
5.5.8. Решение системы уравнений трех моментов и общих трехчленных уравнений. Аналитический способ. Графический способ. Определение чисел влияния. Построение инфлюент усилий Qu и Мu в промежуточных сечениях неразрезной балки и инфлюент реакций Vn 255
5.5.9. Неразрезная балка на упруго оседающих опорах. Уравнение пяти опорных моментов 262
5.6. Арки и простые рамы 263
5.6.1. Общие положения 263
5.6.2. Трехшарнирная арка. Реакции и усилия при постоянной нагрузке. Инфлюенты (линии влияния). Эпюры углов поворота и прогибов арки 263
5.6.3. Статически неопределимые арки. Универсальные формулы для усилий. Характеристики фиктивного профиля. Определение факторов Рф, Lx, Ly. Определение опорных моментов и опорных реакций. Инфлюенты усилий в бесшарнирной арке. Использование общих формул для расчета одно- и двухшарнирной арок. Упруго защемленная арка 266
5.6.4. Двухшарнирная арка. 269
5.6.5. Упрощенный расчет двухшарнирных и бесшарнирных параболических арок. Учет обжатия 270
5.6.6. Одноконтурные (простые) рамы. Статически определимые рамы. Статически неопределимые рамы. Упрощения в расчете геометрических характеристик гибкости и фиктивных нагрузок 272
5.6.7. Бесшарнирные арки и рамы под нагрузкой, перпендикулярной их плоскости 275
5.7. Сложные рамы 276
5.7.1. Классификация методов 276
5.7.2. Расчет рам по способу трех и четырех моментов. Закрепленная эстакада. Свободная эстакада. Простая балка переменного сечения как элемент основной системы. Ступенчатая стойка. Ломаная или криволинейная балка. Уравнение трех моментов для неразрезной балки с пролетами в виде параболических арок с затяжками. Зависимости между перемещениями и уравнения равновесия в сложных случаях 277
5.7.3. Метод перемещений. Общие положения. Формулы для усилий (реакций) защемлений от местной нагрузки или заданной деформации и перемещений торцов. Составление уравнений из условий равновесия. Стандартные формулы для составления уравнений метода перемещений. Канонические уравнения метода перемещений для свободной рамной эстакады 281
6.7.4. Метод сил. Общие положения. Выбор основной системы, составление и решение канонических уравнений. Специальные приемы упрощения и контроля расчета по методу сил. Дополнительная литература 287
5.8 Расчет рам методом последовательных приближений 291
5.8.1. Способ распределения моментов (инженеры А. Н. Газарян и Я. К. Канонов) . Несвободные рамы. Свободные рамы. Многоярусные рамы. Дополнительная литература 291
5.8.2. Способ распределения углов поворота (канд. техн. наук П. М. Сосис) 296
5.8.3. Расчет многоэтажных рам на горизонтальную нагрузку (канд. техн наук доц. Я. Б. Львин). Однопролетная рама. Применение однопролетной схемы к расчету многопролетных рам 298
5.8.4. Метод фокусов (фокусных отношений). Общие положения. Формулы и приемы метода моментных фокусов. Формулы метода угловых фокусов. Область применения метода фокусов 300
5.9. Расчет пространственных рам с взаимно перпендикулярными брусьями по методу перемещений 304
5.9.1. Основные зависимости и формулы 304
5.9.2. Пример 306
5.10. Тонкостенные брусья 307
5.10.1. Прямые тонкостенные брусья с жестким поперечным сечением и пренебрежимо малой жесткостью свободного кручения 307
5.10.2. Тонкостенные брусья с жестким поперечным сечением и конечной жесткостью свободного кручения 309
5.10.3. Кривые тонкостенные брусья и арки с жестким поперечным сечением 311
5.10.4. Рамы из тонкостенных брусьев и бирамы 312
5.10.5. Поперечные изгибающие моменты и учет деформации контура поперечного сечения в тонкостенных брусьях 312
5.10.6. Приближенный расчет тонкостенных брусьев и цилиндрических оболочек с открытым деформируемым поперечным сечением (д-р техн. наук проф. С. Н. Кан и канд. техн. наук доц. П. А. Школьный) 313
5.11. Специальные вопросы 316
5.11.1. Конструкции типа составных брусьев. Многоэтажные рамы под горизонтальной нагрузкой. Каркасно панельные стены. Составная балка с пенсами, работающими на изгиб, и стенкой, работающей на сдвиг. Многопоясные составные брусья 316
5.11.2. Комбинированные и предварительно напряженные конструкции. Комбинированные конструкции. Предварительно напряженные металлические балки 321
5.11.3. Гибкие нити. Общие положения. Провисание непологой нити под действием собственного веса. Пологая нить (канд. техн. наук Р. Н. Мацелинский). Примеры расчета (Р. Н. Мацелинский). Стальные канаты. Дополнительная литература 323
5.11.4. Пневматические конструкции (доц. В. Н. Архангельский и инж А. Н Глухарев). Определения и основные сведения. Особенности расчета ПК. Расчет оболочки, работающей на избыточное давление. Расчет аэробалки. Определение деформаций ПК. Материалы для ПК. Литература 329
РАЗДЕЛ 6. РЕШЕНИЕ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ. Действ, член АСиА СССР д-р техн. наук проф.Б. Н. Жемочкин, д-р техн. наук проф.А. А. Уманский 339
6.1. Способ Гаусса 339
6.1.1. Схемы вычислений 339
6.1.2. Примеры 341
6.1.3. Решение трехчленных уравнений 344
6.1.4. Числа влияния и их определение по способу Гаусса 344
6.2. Способ последовательных приближений (способ итерации) 345
6.3. Решение уравнений с помощью настольных вычислительных машин (инженеры К. П. Вишневский и Б. Л. Тарнопольский) 348
6.3.1. Компактные схемы способа Гаусса 348
6.3.2. Метод квадратных корней 351
6.4. Механизация решений уравнений 351
РАЗДЕЛ 7. ТАБЛИЦЫ ГЕОМЕТРИЧЕСКИХ ХАРАКТЕРИСТИК СЕЧЕНИЙ БРУСЬЕВ. Канд. техн. наук доц. В. В. Новицкий 353
7.1. Геометрические характеристики при растяжении-сжатии и изгибе 353
7.2. Приближенные значения радиусов инерции 362
7.3. Положение центра изгиба некоторых сечений 363
7.4. Геометрические характеристики при свободном кручении 365
7.5. Положение центра изгиба и бимоменты инерции сечений составных профилей 367
7.6. Геометрические характеристики двутавров и швеллеров при свободном и стесненном кручении 368
РАЗДЕЛ 8. ТАБЛИЦЫ ДЛЯ РАСЧЕТА БАЛОК, АРОК И РАМ. Инж. М. С. Волчегорский, инж. Д. Л. Шапиро, д-р техн. наук проф. А. А. Уманский 369
8.1. Балки 369
8.1.1. Эпюры изгибающих моментов и поперечных сил от различных нагрузок 369
8.1.2. Консоль. Опорные реакции, моменты, прогибы и углы поворота концевого сечения 372
8.1.3. Простая балка. Опорные реакции, изгибающие моменты, прогибы, углы поворота опорных сечений, грузовые члены 374
8.1.4. Однопролетные балки с одним защемленным и другим шарнирно опертым концом и с обоими защемленными концами. Опорные реакции и опорные моменты 384
8.1.5. Прогибы однопролетных балок с одним защемленным и другим шарнирно опертым концом и с обоими защемленными концами 389
8.1.6. Прогибы в сечениях с простой балки от сосредоточенного груза Р в сечении х 390
8.1.7. Коэффициенты приведения нагрузки к эквивалентной равномерно распределенной интенсивностью Pэк для определения опорных моментов в неразрезных балках 393
8.1.8. Неразрезные равнопролетные балки. Изгибающие моменты, поперечные силы и опорные реакции от различных нагрузок а) Двух-, трех-, четырех- и пятипролетные балки. б) Бесконечная балка с равными пролетами. в) Определение абсциссы (х0) максимальных пролетных моментов в неразрезных балках 394
8.1.9. Неразрезные равнопролетные балки. Моменты, поперечные силы в сечениях (через 0.1l) и опорные реакции от равномерно распределенной нагрузки: постоянной g и временной р (таблицы Винклера) 401
8.1.10. Неразрезные равнопролетные балки. Моменты, поперечные силы а различных сечениях и опорные реакции от сосредоточенных грузов: постоянных G и временных Р 403
8.1.11. Опорные моменты в неразрезных равнопролетных балках с одним защемленным концом 406
8.1.12. Опорные моменты в неразрезных равнопролетных балках с обоими защемленными концами 406
8.1.13. Прогибы в равнопролетных неразрезных балках (в середине пролета) 408
8.1.14. Опорные моменты в неразрезных равнопролетных балках при осадке опор а) Двух-, трех-, четырех- ч пятипролетные балки. б) Полубесконечная балка. в) Бесконечная балка 410
8.1.15. Ординаты инфлюент (линий влияния) изгибающих моментов и поперечных сил для неразрезных равнопролетных балок 411
8.1.16. Данные для расчета однопролетных подкрановых балок под один кран 413
8.1.17. Данные для расчета неразрезных пятипролетных балок с равными пролетами под два одинаковых крана. Огибающие эпюры М и Q 414
8.1.18. Данные для расчета балок и ригелей рам с вутами а) Симметричная шарнирно опертая по концам балка с вутами. б) Симметричная с защемленными концами балка с вутами. в) Балка с левым односторонним вутом, шарнирно опертая по концам .г) Балка с левым односторонним вутом, защемленная левым концом и шарнирно опертая правым .д) Балка с левым односторонним вутом и обоими защемленными концами. е) Неразрезные равнопролетные балки с симметричными вутами 417
8.1.19. Ординаты инфлюент опорного момента бесконечной балки на упруго оседающих опорах 423
8.1.20. Ординаты инфлюент опорного момента Мг полубесконечной балки на упруго оседающих опорах 423
8.1.21. Данные для расчета перекрытий с перекрестными балками (кессонные перекрытия).а) Схемы распределения нагрузки в перекрестных балках. б) Нагрузки и изгибающие моменты в перекрестных балках при квадратных в плане перекрытиях 424
8.1.22. Усилия в элементах шпренгельной балки. а) Статически определимый шпренгель. б) Статически неопределимый шпренгель 425
8.1.23. Данные для расчета балок с защемленными концами, с ломаной в плане осью 427
8.2. Арки 430
8.2.1. Геометрические данные осей параболической и круговой арок 430
8.2.2. Симметричные трехшарнирные арки любого очертания. Распоры, опорные реакции и изгибающие моменты от различных нагрузок 431
8.2.3. Трехшарнирные круговые и параболические арки. Опорные реакции, изгибающие моменты, поперечные и продольные силы от равномерно распределенной нагрузки 433
8.2.4. Трехшарнирная параболическая арка. Изгибающие моменты в различных сечениях, опорные реакции и распоры от сосредоточенного груза 435
8.2.5. Трехшарнирная параболическая арка. Изгибающие моменты в различных сечениях, опорные реакции и распоры от односторонней частичной равномерно распределенной нагрузки 435
8.2.6. Трехшарнирная параболическая арка. Изгибающие моменты в различных сечениях, опорные реакции и распоры от односторонней частичной равномерно распределенной нагрузки 436
8.2.7. Двухшарнирная параболическая арка. Изгибающие моменты, распоры и опорные реакции от различных нагрузок 437
8.2.8. Двухшарнирная параболическая арка. Изгибающие моменты в различных сечениях, распоры и опорные реакции от действия вертикальной сосредоточенной силы 440
8.2.9. Двухшарнирная параболическая арка. Изгибающие моменты в различных сечениях, опорные реакции от симметричной равномерно распределенной нагрузки 441
8.2.10. Двухшарнирная параболическая арка. Изгибающие моменты в различных сечениях, распоры и опорные реакции от симметричной частичной равномерно распределенной нагрузки 442
8.2.11. Бесшарнирные параболические арки а) Изгибающие моменты, распоры и опорные реакции от различных нагрузок. б) Инфлюенты распора, опорной реакции, опорного момента и момента в середине пролета 443
8 2.12. Дополнительные геометрические данные для параболических, круговых и эллиптических арок 447
8.2.13. Бесшарнирная параболическая арка постоянной толщины. Изгибающие моменты, распоры и опорные реакции от различных нагрузок 447
8.2.14. Поправочные коэффициенты для определения усилий в бесшарнирной параболической арке переменной толщины 449
8.2.15. Опорные моменты от собственного веса бесшарнирных параболических арок переменной толщины 449
8.2.16. Бесшарнирная круговая арка постоянной толщины. Изгибающие моменты, распоры и опорные реакции от различных нагрузок 450
8.2.17. Поправочные коэффициенты для определения усилий в бесшарнирной круговой арке переменной толщины 452
8.2.18. Опорные моменты и распоры от собственного веса бесшарнирных круговых арок переменной толщины 452
8.2.19. Бесшарнирная эллиптическая арка постоянной толщины. Изгибающие моменты, распоры и опорные реакции от различных нагрузок 453
8.2.20. Поправочные коэффициенты для определения усилий в бесшарнирной эллиптической арке переменной толщины 454
8.3. Рамы 455
8.3.1. Моменты в Г-образной раме с горизонтальным или наклонным ригелем. а) Ригель и стойка шарнирно оперты. б) Ригель шарнирно оперт, стойка защемлена 455
8.3.2. Моменты в Г-образной раме с горизонтальным или наклонным защемленным ригелем и защемленной стойкой 457
8.3.3. Моменты в Т-образной раме с шарнирно опертым ригелем и защемленной стойкой 459
8.3.4. Моменты в Т-образной раме с защемленными ригелем и стойкой 461
8.3.5. Моменты и реакции П-образной рамы с шарнирно прикрепленным ригелем. а) Стоики постоянного сечения. б) Стойки ступенчатого сечения 463
8.3.6. Моменты и реакции П-образной рамы. а) С шарнирно прикрепленными стойками. б) С защемленными стойками 465
8.3.7. Моменты в Г-образной раме с горизонтальным или наклонным шарнирно опертым ригелем и ступенчатой защемленной стойкой 467
8.3.8. Моменты в Г-образной раме с горизонтальным или наклонным защемленным ригелем и ступенчатой защемленной стойкой 468
8.3.9. Моменты в Т-образной раме с шарнирно опертым ригелем и ступенчатой защемленной стойкой 470
8.3.10. Моменты в Т-образной раме с защемленным ригелем и ступенчатой защемленной стойкой 472
8.3.11. Простые симметричные рамы. Вспомогательные формулы к 5.6.6 а) Характеристики гибкости рамы, увеличенные в ЕI раз. б) Эпюры M и фиктивные нагрузки ломаного ригеля приведенные к точкам А, С, В. в) Эпюры М и фиктивные нагрузки левой ступенчатой стойки, увеличенные в ЕI раз. Моменты и реакции ступенчатой стойки, защемленной на одном конце и шарнирно опертой на другом конце 474
8.3.12. Моменты и реакции ступенчатой стойки, защемленной на одном конце и шарнирно опертой на другом конце 477
8.3.13. Коэффициенты k0 для определения в ступенчатых стойках: а) перемещения верха защемленной внизу стойки от силы Х=1. б) реакции Нb в случае стойки, защемленной внизу и шарнирно опертой наверху, от взаимного горизонтального смещения опор на =1; в) реакции Нb от поворота нижнего сечения на угол = 1 479
8.3.14. Ступенчатая стойка с защемленным нижним и шарнирно опертым верхним концом. а) Реакции Нb от действия момента Мв = Ра. б) Реакции Hb от действия момента Ми=Ран. в) Реакции Hb от действия горизонтальной силы Р. г) Реакции Нb от действия горизонтальной силы Pн. д) Реакции Нb от действия горизонтальной равномерно распределенной нагрузки рв. е) Реакции Нb от действия горизонтальной равномерно распределенной нагрузки рн. ж) Реакции Нb от действия горизонтальной равномерно распределенной нагрузки по всей высоте стойки. з) Реакции Нb от действия горизонтальной треугольной нагрузки 480
8.3.15 Моменты и реакции ступенчатой стойки с защемленными концами 487
8.3.16. Ступенчатая стойка с защемленными концами. Моменты защемления при различных n и l.а) от поворота верхнего сечения на угол = 1; б) от поворота нижнего сечения на угол =1; в) от взаимного смещения опорных сечений на =1; г) от равномерно распределенной нагрузки; д) от сосредоточенной силы; е) от внешнего момента 488
8.3.17. Расчет одноэтажных многопролетных рам с шарнирно опертыми ригелями и ступенчатыми защемленными стойками. а) Горизонтальная сосредоточенная нагрузка. б) Горизонтальная равномерно распределенная нагрузка. в) Действие внешнего момента на стойку рамы. г) Примеры 491
8.3.18. Изгибающие моменты в одноэтажных многопролетных рамах. а) Двухпролетные рамы. б) Трехпролетные рамы. в) Четырехпролетные рамы. г) Примеры 495
8.3.19. Изгибающие моменты в ригелях многоэтажных рам с равными пролетами 503
8.3.20. Формулы для подсчета интегралов Мора 506
8.4. Балки на упругом (винклеровском) основании 508
8.4.1. Гиперболо-круговые функции для расчета балок на упругом основании и цилиндрических резервуаров 508
8.4.2. Начальные параметры балок на упругом основании 513
8.4.3. Затухающие функции для расчета балок на упругом основании и цилиндрических резервуаров 514
8.4.4. Перемещения и усилия полубесконечной балки от сосредоточенной силы Р= 1 (инфлюенты) 516
8.4.5. Перемещения и усилия полубесконечной балки от сосредоточенного момента L= 1 (инфлюенты) 517
РАЗДЕЛ 9. БРУСЬЯ, ОЧЕРЧЕННЫЕ ПО ДУГЕ КРУГА, И КРУГОВЫЕ КОЛЬЦА. Канд. техн. наук доц. Ю. П. Григорьев 519
9.1. Нагрузка в плоскости кривизны 519
9.1.1. Круговые брусья. Основные обозначения и общие указания. Формулы для усилий и перемещений при простейших нагрузках. Общие формулы для усилий и перемещений. Усилия в ключевом сечении бруса, защемленного двумя концами 519
9.1.2. Круговые кольца. Формулы для усилий и перемещений при простейших нагрузках. Расчет круговых шпангоутов. Формулы для расчета круговых колец, нагруженных произвольным числом сосредоточенных сил и моментов 524
9 2. Нагрузка, перпендикулярная плоскости кривизны 531
9.2.1. Круговые брусья. Основные обозначения и общие указания. Формулы для усилий и перемещений кругового бруса при простейших нагрузках. Общие формулы для расчета 6pуca, нагруженного сосредоточенными силами и моментами. Усилия в ключевом сечении тонкостенного бруса, защемленного двумя концами. Монорельс на трех и на четырех равноотстоящих опорах 531
9.2.2. Расчет массивных и тонкостенных круговых колец при статически определимом опирании 541
9.2.3. Расчет круговых колец на равноотстоящих опорах 546
9.3. Брусья большой кривизны. Напряжение при изгибе. Перемещения при изгибе в плоскости кривизны 551
Раздел 10. ФЕРМЫ. Канд. техн. наук А. Г. Иммерман 553
10.1. Плоские фермы 553
10.1.1. Элементы и классификация плоских ферм 553
10.1.2. Основные положения расчета 553
10.1.3. Определение усилий в статически определимых фермах при неподвижной нагрузке. Установление неработающих стержней и стержней, усилия в которых определяются местной нагрузкой. Аналитическое определение усилий. Графическое определение усилий. Определение усилий по готовым формулам, таблицам и графикам. Расчет ферм на внеузловую нагрузку. Расчет составных ферм. Фермы с гибкими пересекающимися раскосами. Фермы с «окном». Способ замены стержней. Тонкостенные фермы. Распорные и комбинированные фермы 555
10.1.4. Перемещения узлов статически определимых ферм. Исходные данные для определения перемещений. Аналитическое определение перемещений. Графическое определение перемещений. Построение эпюры прогибов пояса фермы по способу фиктивных грузов 560
10.1.5. Инфлюенты усилий и перемещений в статически определимых фермах. Статический способ построения инфлюент усилий. Кинематический способ построения инфлюент усилий. Инфлюента перемещения. Невыгодная установка грузов на инфлюенте 563
10.1.6. Определение усилий в статически неопределимых фермах при неподвижной нагрузке. Приближенные способы расчета. Метод сил. Метод заданных напряжений. Фермы с нецентрированными узлами. Учет жесткости узлов. Учет защемления ферм, жестко связанных с колоннами. Работа нулевых стержней. Проверка расчета ферм 566
10.1.7. Определение перемещений в статически неопределимых фермах 569
10.1.8. Инфлюенты усилий в статически неопределимых фермах 569
10.2. Плоские фермы, соединенные связями (биконструкции) 570
10.2.1. Определение и классификация 570
10.2.2. Основные положения расчета 570
10.2.3. Определение усилий в биконструкциях 571
10.2.4. Статически неопределимые и многорядные биконструкции 572
10.3. Пространственные фермы 573
10.3.1. Классификация и основные положения образования и расчета 573
10.3.2. Общие методы определения усилий 574
10.3.3. Расчет куполов 576
10.3.4. Расчет башен и мачт 576
10.4. Предварительно напряженные фермы 577
10.4.1. Определение. Основные положения расчета и конструирования 577
10.4.2. Фермы с предварительно напряженными отдельными стержнями 577
10.4.3. Предварительно напряженные фермы с затяжками 578
РАЗДЕЛ 11. ТЕОРИЯ УПРУГОСТИ. Д-р техн. наук проф. И. И. Гольденблат 581
11.1. Основные уравнения теории упругости 581
11.1.1. Уравнения равновесия 581
11.1.2. Уравнения совместности деформаций 582
11.1.3. Определение перемещений по заданным составляющим тензора деформаций 583
11.1.4. Схемы решения задач теории упругости. Уравнения Ляме 584
11.1.5. Потенциальная энергия деформации. Начало наименьшей работы 585
11.1.6. Некоторые частные решения 585
11.2. Плоская задача 585
11.2.1. Плоское напряженное состояние 585
11.2.2. Плоская деформация 585
11.2.3. Функция напряжений для плоской задачи 586
11.2.4. Плоская задача в полярных координатах 586
11.2.5. Сведение плоской задачи к задаче об изгибе пластинки 587
11.3. Вариационные методы решения задач теории упругости 588
11.3.1. Метод Ритца 588
11.3.2. Метод Галеркина 590
11.3.3. Метод Треффца (метод смягчения граничных условий) 591
11.4. Метод сеток 591
11.4.1. Тринадцатичленное уравнение 591
11.4.2. Применение метода конечных разностей к расчету балки-стенки 592
11.5. Сводка некоторых решений теории упругости 594
11.5.1. Чистый изгиб 594
11.5.2. Поперечный изгиб консоли 594
11.5.3. Поперечный изгиб балки 595
11.5.4. Изгиб кривого бруса (задача X. С. Головина) 596
11.5.5. Клин, сжатый сосредоточенной силой 596
11.5.6. Толстостенные цилиндры и сферический сосуд 596
11.5.7. Упругая полуплоскость и упругое полупространство 597
11.6. Концентрация напряжений 597
11.6.1. Концентрация напряжений при растяжении 597
11.6.2. Концентрация напряжений при изгибе (инж. Г. Ю. Ратновская). Балка с круглым отверстием. Балка с отверстием квадратной формы 598
11.7. Кручение стержня прямоугольного поперечного сечения 599
11.8. Балки-стенки 600
11.8.1.Однопролетная балка-стенка 600
11.8.2. Многопролетная балка-стенка 600
11.9. Панели крупнопанельных и каркасно-панельных зданий 605
РАЗ
4. Предварительно напряженные конструкции
При обследовании конструкций необходимо
выявить возможные отклонения от проекта
при изготовлении и монтаже конструкций.
Не исключено, что
конструкции имели начальные напряжения
еще до загружения их нагрузкой.
Например, монтаж многопролетных балок,
плит, пространственных конструкций
на опоры с разными отметками изменяет
ихнапряженно-деформированное
состояние. При усилении эксплуатируемых
конструкций часто применяют приемы по
регулированию усилий, используют
затяжки, шпренгеля, тяжи, распорные
элементы, т. е. применяют приемы
предварительного напряжения конструкций.
Поскольку эта тема мало знакома
студентам, в этой главе сделана попытка,
напомнить основыпредварительного
напряжения конструкций и обобщить
известные и новые приемы создания
преднапряжения при изготовлении новых
и усилении эксплуатируемых конструкций.
При этом большего эффекта от преднапряжения
можно добиться при усилении конструкций,
находящихся под нагрузкой, изменяя
их напряженное состояние в больших
диапазонах. Крайние волокна сечения
нагруженных элементов можно разгрузить
до нуля, а затем загрузить до напряжений
обратного знака равных расчетному
сопротивлению. В новых конструкциях
такого эффекта достичь нельзя. Однаконужно помнить, что
на предварительное напряжение конструкций
затрачивается дополнительная
энергия, требуется контроль величин
натяжениязатяжек,
более качественное выполнение и
повышенная трудоемкость изготовления.
Все это нужно учитывать при сравнении
вариантов усиления конструкций.
Предварительно
напряженными называются
конструкции, в которых напряжения
от расчетной нагрузки складываются с
дополнительныминапряжениями,
искусственно созданными различными
способами в период изготовления, монтажа
или эксплуатации конструкции. В отличие
от обычных, где напряжения
возникают только от расчетной нагрузки,
в сечениях предварительно напряженных
конструкций принудительно создаются
новые напряжения либо до работы
конструкции, либо в период ее работы
под
62
нагрузкой. При этом напряжения в наиболее
загруженных сечениях имеют чаще
всего другой знак, чем от нагрузки.
4.1. Цели предварительного напряжения
Для каких целей
создается предварительное напряжение
конструкций?
Такими целями могут быть:
1. Создание эффективной
по расходу материала конструкции.
2. Использование
высокопрочной стали, применение которой
в
обычной
конструкции нерационально, т. к.
механические свойства ее используются
не полностью, а стоимость несколько
выше обычной стали.
Применение работающих
только на растяжение мембран
(тонких
листов),
тросов, канатов и других гибких элементов
в конструкциях, воспринимающих
также и сжимающие усилия.Уменьшение
деформативности (прогибов, колебаний,
трещин)
конструкций.Расширение области
применения прокатных профилей за
счет
снижения
максимальных расчетных усилий.Увеличение несущей способности и
жесткости эксплуатируемой
конструкции
при ее усилении.
Можно ли считать, что предварительно
напряженные конструкции более прочные,
чем обычные?
Нет, если они рассчитаны (запроектированы)
на одну и ту же расчетную
нагрузку. Например, плиты и балки
перекрытий могут быть с пред-напряжением
и без, однако их несущая способность
одинакова. При этом армирование
разное, в предварительно напряженных
конструкциях сечение высокопрочной
арматуры меньше.
Да, если обычная конструкция получает
дополнительное напряжение.
Достижение указанных выше целей
обеспечивает преимущества предварительно
напряженных конструкций по сравнению
с обычными. Но, нужно помнить, что для
создания предварительного напряжения
необходимо
выполнить ряд приемов, требующих
дополнительных затрат и устройств,
более высокой ответственности исполнителей
и контроля за создаваемыми
усилиями преднапряжения.
В то же время после
глубокого изучения этой проблемы можно
сделать вывод, что все неточности
изготовления, монтажа обычных конструкций
могут стать причинами возникновения
дополнительных напряжений, неучтенных
расчетом, что в одних случаях повышает,
а в других — понижает несущую способность
конструкций. Таким образом, не намеренно
создаются предварительно напряженные
конструкции в период изготовления
или монтажа, что отражается на их несущей
способности.
63
4.2.
Работа предварительно напряженных
конструкций
Область применения предварительного
напряжения обширна. Практически все
конструкции: плиты, балки, фермы, арки,
рамы и пространственные
конструкции, как новые, так и эксплуатируемые,
могут быть предварительно напряженными.
Ряд же конструкций, например из гибкихэлементов, без
предварительного напряжения не могут
существовать, т. к. не
могут воспринимать даже незначительных
сжимающих напряжений. Это тросовые
фермы, мембранные большепролетные
покрытия и т. д. [66].
Самый крупный в Европе зал на 45 тысяч
зрителей в крытом стадионе спорткомплекса
«Олимпийский» на проспекте Мира в
Москве. Здание
имеет эллиптическую форму плана с
размерами по главным осям 224×183 м.
Покрытие выполнено в виде мембранной
висячей оболочки со стрелой провисания
12,5 м из нержавеющего листа (сталь 14Г2)
толщиной 5мм,
совмещающего несущие и ограждающие
функции. Мембрана крепилась с
натяжением высокопрочными болтами к
провисающим радиальным фермам высотой
2,5 м и к опорному кольцу из монолитного
железобетона в стальной опалубке
сечением 5×1,75 м. Работая совместно с
радиальными фермами мембрана
воспринимает все вертикальные (350—500
кг/м2) и ветровуюнеравновесную
нагрузки. При этом общий расход металла
на покрытие небольшой — 107 кг/м2(благодаря применению тонких гибких
листов ипреднапряжения).
Проанализируем
работу предварительно напряженных
конструкций
на следующих примерах:
1. Тросовая ферма.
64
Она состоит из
поясов и раскосов, выполненных из тросов.
От эксплуатационной нагрузки во
всех элементах фермы возникают осевые
усилия: сжатия или растяжения. Пусть
в верхнем поясе элемент А—В воспринимает
от нагрузки усилие сжатия величинойN
= 2500 кН. Как воспринятьэто
усилие гибкому тросу?
Вероятно, этот элемент еще до воздействия
эксплуатационной нагрузки
должен быть растянут силой, превышающей
расчетное усилие, напримерNo
= 3000 кН. Этого можно достичь преднапряжением
фермы — натяжением оттяжек3 на
анкерные фундаменты4. Тогда при
работе фермы на эксплуатационную
нагрузку суммарные усилия в элементе
А—В будут равны ΣN=
3000 — 2500 = 500 кН. Элемент остается растянутым,
следовательно,
не может потерять устойчивость.
Аналогичные фермы пролетом 874 м были
возведены в мостовом переходе через
реку Волга во время строительства
Волжской ГЭС (рис. 4.1).
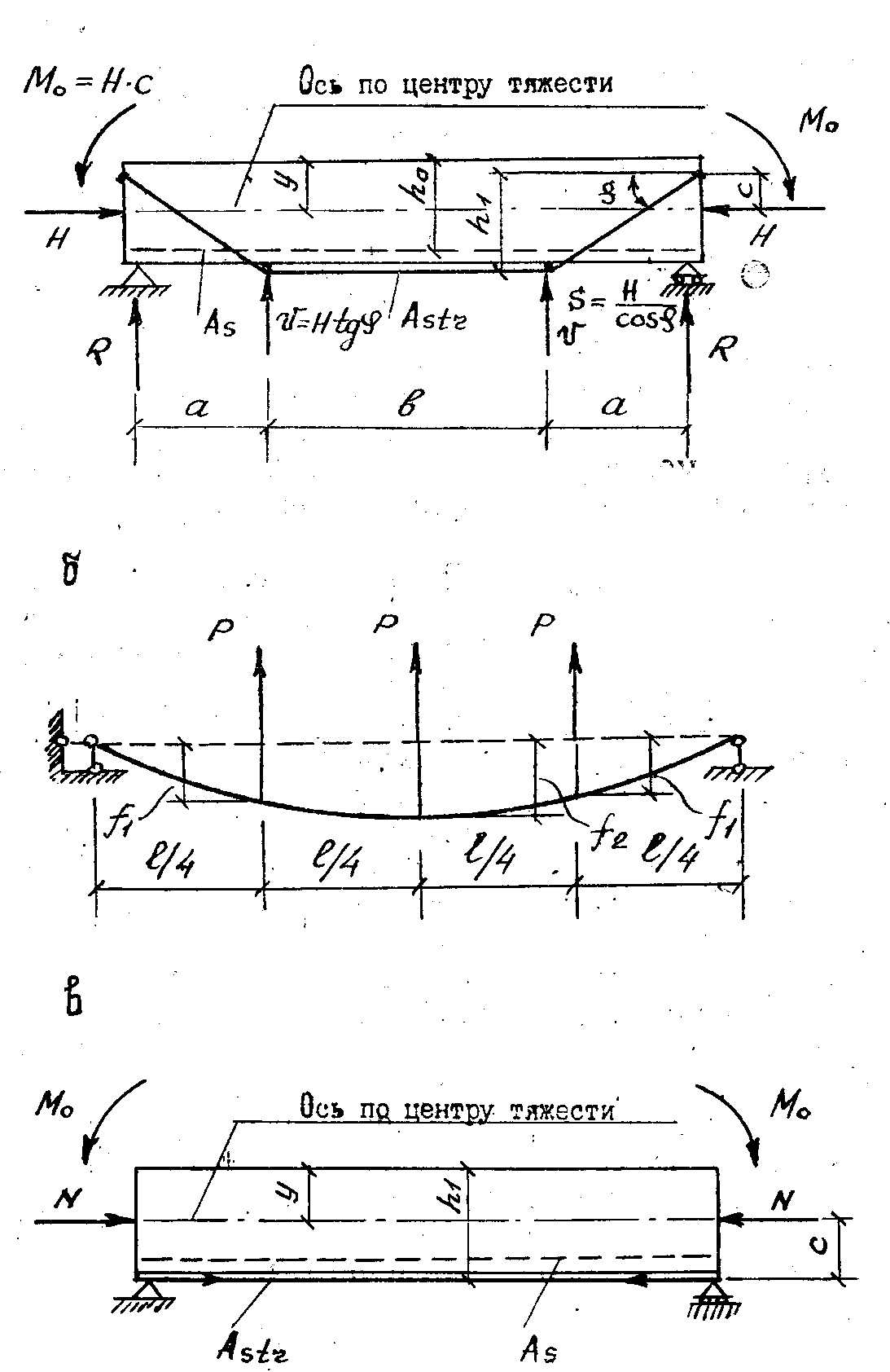
2. Балка с затяжкой (рис. 4.2).
При натяжении затяжки
силой N‘3
в балке, как
от внешней силы,
приложенной с эксцентриситетом е
относительно оси, проходящей через
центр тяжести сечения балки, возникают
нормальные напряжения от момента
выгибаM3
=N‘3e
и сжимающей силыN6
= N‘3
. Величины их соответственно
для верхних и нижних волокон балки
равны:
где Аб— площадь сечения балки;Wв иWн
— соответственно моменты сопротивления
сечения для верхних и нижних волокон
балки.
Как видно, кроме
выгиба, балка дополнительно обжимается
по всему сечению,
чего при таких схемах балок избежать
не удается. Положительный
эффект частично погашается, однако в
балке остаются напряжения,
обратные по знаку напряжениям от
эксплуатационной нагрузки. Вдальнейшем
от эксплуатационной нагрузки балка с
затяжкой работает как однажды
статически неопределимая система, в
результате в затяжке появляются
дополнительные усилия растяженияN‘3
, которые получили название
усилий
самонатяжения. От
них все сечение балки получит аналогич-
65
ные дополнительные напряжения и основные
напряжения от нагрузки. Таким образом,
суммарные напряжения в балке от сил
преднапряжения, самонатяжения
и эксплуатационной нагрузки равны:
где Мв, M‘3
и M״3
— изгибающие моменты, соответственно
от внешней нагрузки,сил
преднапряжения и самонатяжения в
затяжке.
Суммарные напряжения
не должны превышать расчетного
сопротивления материала балки R.
Поскольку
напряжения от преднапряжения в балке
имеют другой знак, чем от нагрузки, то
абсолютная величина напряжений от
нагрузки может быть значительно больше
R.
Таким образом,
балка с затяжкой имеет большую несущую
способность, чем без затяжки. При одной
и той же нагрузке предварительно
напряженная балка с затяжкой по расходу
металла экономичней обычной балки за
счет применения затяжки из высокопрочной
стали. Аналогичный эффект получается
и в предварительно напряженных
железобетонных конструкциях, где вместо
обычной вводят предварительно растянутую
высокопрочную арматуру, которую в
обычных конструкциях применять
нерационально, так как в бетоне возникают
трещины раньше, чем в арматуре напряжения
близкие к расчетному сопротивлению.
3. Двухнролетная неразрезная балка
(рис. 4.3). Регулированиемуровнями
опор (осадками опор) можно изменять
состояние балки по ее длине.
Рассмотрим этот прием на примере.
66
Пример 1. Пусть балка
пролетами / проектируется* постоянного
сечения, т. е. из одного профиля (рис.
4.3, а). Максимальный расчетный момент в
двухпролетной балке от равномерной
нагрузки над средней опорой составитМ1= 0,125ql2,
в то время как в пролетах моменты не
болееМ2≤ 0,07ql2
(рис. 4.3, б). Можно ли снизить максимальное
значение момента и выровнять пролетные
с опорным? Пусть средняя опора ниже
крайних на величину Δ. Тогда двухпролетная
балка превращается в однопролетную
(рис. 4.3, в, г) с удвоенным пролетом21,
пока ее прогиб от части нагрузкиq1
в середине (над средней опорой) не
достигнет величины Δ. Только после этого
на оставшуюся нагрузкуq2
балка будет работать как двухпролетная
(рис. 4.3, д, е). Суммарные моменты в сечениях
балки уже будут другими: меньше над
средней опорой и больше в пролетах.
Проектируя балку уже на уменьшенное
значение максимального момента, получают
экономию металла. Покажем это на примере.
67
Пример
2. Если предполагается запроектировать
балку переменного сечения,
то целесообразно наоборот увеличить
опорный момент над средней опорой за
счет уменьшения пролетных моментов при
поднятии средней опоры на величину Δ1.
Методику проектирования можно предложить
следующую: задать минимально возможное
сечение балки по конструктивным
соображениям, определить ее несущую
способность, затем найти величину Δ1;
и соответствующий опорный момент.
68
На увеличенный
опорный момент подобрать усиленное
сечение балки вблизи средней
опоры.
Приведенные
примеры отражают лишь часть приемов
создания предварительно
напряженных конструкций. В действительности
их много. Попытаемся эти приемы
систематизировать.
Преднапряженная составная деревянная балка
Изобретение относится к области строительства и может быть использована в качестве балок перекрытий жилых и общественных зданий.
Известна деревянная балка, включающая склеенный пакет досок, обоймы по концам балки, предварительно напряженную арматуру (см. а/с СССР №339649, Е04С 3/18, 1970, опубл. в бюл. №17, 24.05.1972).
Недостатками преднапряженной деревянной балки являются: трудоемкость изготовления, малая эффективность преднапряжения. Сначала надо изготовить балки обоймы с проволочной арматурой, кожух для проволочной арматуры, затем смонтировать обоймы с арматурой и кожух. Продольные преднапряженные стержни, расположенные в нижней зоне поперечного сечения балки, используются неэффективно, балка обладает малой несущей способностью.
Известна деревянная преднапряженная балка включающая балку с закрепленной на ней гибкой арматурой и натяжным устройством в виде стяжных болтов (см. патент Франции №2046397 21/00, 1970).
Недостатками деревянной преднапряженной балки являются затрудненность регулировки напряжения в арматуре, сложность натяжных устройств.
Наиболее близкой является преднапряженная деревянная балка, включающая склеенный пакет досок, обоймы на концах балки и предварительно напряженную арматуру (см. а/с СССР №1244259 Е04 3/18, опубл. в бюл. №26 от 15.07.1986 г.).
Недостатками преднапряженной деревянной балки являются: слабая несущая способность сжатой зоны балки, крепежные элементы преднапряженных гибких стержней громоздки, слабая несущая способность опорной зоны балки из-за ее ослабления громоздким дерелаксационным натяжным узлом.
Изобретение направлено на повышение общей несущей способности деревянной балки за счет усиления сжатой зоны, сохранения опорной зоны балки при увеличении эффекта преднапряжения от продольных стержней.
Результат достигается тем, что в деревянной балке, включающей склеенный пакет досок, монолитный вкладыш, имеющая продольные преднапряженные арматурные стержни, согласно изобретению в торцевой части балки установлены пластины с деформируемой прокладкой и из пружинистого материала, к которым закреплены концы продольных арматурных стержней, при этом пластина в своей середине опирается на ссуженный торец вкладыша.
Результат достигается также тем, что вкладыш выполнен из монолитного древесного пластика или из полимербетона и соединен со слоями балки посредством анкеров, расположенных с переменным шагом, а продольные стержни преднапряжены по дуге их провисания, кривизна которых обеспечивается горизонтальными стержнями размещенными по огибающей эпюры моментов.
На фиг. 1 изображена преднапряженная составная деревянная балка, состоящая из пакета досок, поперечных пластин, вкладыша, анкеров и ветвей преднапряженных стержней; на фиг. 2 — вид сверху составной деревянной балки; на фиг. 3, 4 — сечения А-А, Б-Б балки (фиг. 1).
Преднапряженная составная деревянная балка включает пакет досок 1, вертикальные анкера 3, поперечные стержни 4, ветви продольные стержней 5 и 6, монолитный вкладыш 2, пластины 7. Поперечные стержни 4 размещены по огибающей эпюры моментов. На концах ветвей продольных стержней 5 и 6 нарезана резьба под гайки 8, размещены пластины 7 из пружинистого материала с подкладкой 9. На пластинах 7 выполнены отверстия под ветви продольных арматурных стержней 5 и 6, через которые они натянуты гайкой 8.
В заводских условиях сначала подготавливают доски с заранее намеченными отверстиями под продольные арматурные стержни 5 и 6, выполняют склеивание досок 1, делают отверстия и вставляют на клею поперечные стержни 4. На концах ветвей стержней 5 и 6 нарезают резьбу, пропускают продольные стержни 5 и 6 через отверстия пакета досок 1. На поперечных торцевых пластинах 7 из пружинистого материала (например, сталь, текстолит) делают отверстия под ветви продольных стержней 5 и 6, надевают поперечные пластины 7 на ветви стержней 5 и 6 с обоих концов балки натяжители — гайки 8. После подготовительных процедур производят замоноличивание вкладыша древесным пластиком (фиг. 1) или фибробетоном, полимербетоном. Затем после приобретения монолитного вкладыша гостированной прочности натягивают гибкие продольные стержни 5 и 6, создавая гайкой 8 преднапряжение (фиг. 1).
Опирание торцевой пластины 7 по своей середине на ссуженные торцы вкладыш 2 и наличие деформируемой подкладкой 9 обеспечивает выравнивание усилий преднапряжения в ветвях арматуры 5, 6. Пружинистость материала пластины 7 придает дерелаксационные свойства натяжному узлу.
Создание преднапряжения ветвей продольной гибкой арматуры и наличие вкладыша увеличивает жесткость и несущую способность составной деревянной балки, по нормальному и по наклонному сечениям, благодаря расположению продольных арматур по дуге ее провисания и использования пластины с дерелаксационными свойствами.
Собранная преднапряженная составная деревянная балка обладает повышенной жесткостью, несущей способностью и надежностью, а также уменьшенной материалоемкостью.
Дизайн моста | Конструкция сборных бетонных мостовых балок только в соответствии с BS 5400
сталь в зоне растяжения следует учитывать:
Центроид сухожилий в зоне растяжения = (6 × 60 + 10 × 110 + 8 × 160 +
4 × 260) / 28 = 135 мм
Эффективная глубина от уровня 3 = 1200 — 135 = 1065 мм
Предположим, что
максимальное расчетное напряжение создается в сухожилиях, тогда:
Сила растяжения в сухожилиях Fp = 0.87 × 28 × 139 × 1670 × 10-3 = 5655
кН
Компрессионный
усилие в бетонном фланце:
F f = 0,4 × 40 × 1000 × 150 × 10 -3 = 2400 кН
Пусть X = глубина до нейтральной оси.
Сила сжатия в бетонном полотне:
F w = 0,4 × 50 × [393 — (393 — 200) × (X — 150) / (671 ×
2)] × (X — 150) × 10 -3
F w = (-2.876X 2 + 8722.84X — 1243717) × 10 -3
Приравнивая силы для получения X:
5655 = 2400 + (-2,876 × 2 + 8722,84X — 1243717) × 10 -3
X = 659 мм
Напряжение в сухожилиях
после потерь = f pe = 4144 × 10 3 / (32 × 139) =
932 Н / мм 2
Prestrain ε pe = f pe
/ E s = 932/200 × 10 3 = 0.0047
Определить глубину до
нейтральная ось с помощью итеративного анализа совместимости деформаций
Попробуйте X = 659 мм в качестве начальной оценки
Ширина полотна на этой глубине = 247 мм
ε pb6 =
ε 6 + ε pe = -459 × 0,0035 / 659 + 0,0047 = 0,0022
ε pb5 =
ε 5 + ε pe =
-359 * 0.0035/659 + 0,0047 = 0,0028
ε pb4 =
ε 4 + ε pe =
281 * 0,0035 / 659 + 0,0047 = 0,0062
ε пб3 =
ε 3 + ε pe =
381 * 0,0035 / 659 + 0,0047 = 0,0067
ε pb2 =
ε 2 + ε pe =
431 * 0,0035 / 659 + 0,0047 = 0,0069
ε pb1 =
ε 1 + ε pe =
481 * 0.0035/659 + 0,0047 = 0,0072
f pb6 = 0,0022 × 200 × 10 3 = 444 Н / мм 2
f pb5 = 0,0028 × 200 × 10 3 = 551 Н / мм 2
f pb4 = 1162 + 290 × (0,0062 — 0,0058) / 0,0065 = 1178 Н / мм 2
f pb3 = 1162 + 290 × (0,0067 — 0,0058) / 0,0065 = 1201 Н / мм 2
f pb2 = 1162 + 290 × (0,0069 — 0,0058) / 0.0065 = 1213 Н / мм 2
f pb1 = 1162 + 290 × (0,0072 — 0,0058) / 0,0065 = 1225 Н / мм 2
Сила растяжения в сухожилиях:
Суммарные напряжения в предварительно напряженной балке
предварительно напряженный бетон — это передовая технология. Использование предварительно напряженного бетона в последнее время увеличилось, особенно для больших конструкций, таких как мосты и высотные здания. Понять, как предварительное напряжение бетона улучшит свойства конструкции. полезно построить диаграмму напряжений для стержня до и после предварительного напряжения.
1. Балка с простой опорой и собственным весом
только для свободно опертой балки, подверженной действию собственной нагрузки. Напряжение изгиба может быть рассчитано с использованием теории упругой балки f = M.C / I. длина нижнего волокна под действием собственного веса увеличится, что вызовет растягивающее напряжение, как показано на рисунке ниже. противоположное произойдет с верхним волокном. у верхнего волокна длина будет уменьшаться, что приведет к сжатию. бетон прочнее на сжатие.поэтому нижняя часть элемента треснет и выйдет из строя, если нагрузка превысит допустимый предел.
2. Балка с простой опорой и собственным весом.
и осевое предварительное напряжение
сила
Для усиления члена и уменьшения натяжения нижнего волокна. мы приложим усилие предварительного напряжения PT к центру стержня. это вызовет равномерное осевое напряжение, равное PT / A, как показано на рисунке ниже. в результате сжатие в нижнем волокне будет уменьшено, как показано на рисунке ниже.
3. Балка с простой опорой и собственным весом.
и осевое усилие предварительного напряжения
с эксцентриситетом
Для усиления эффекта прижимной силы. мы будем применять PT с эксцентриситетом, равным e. в результате сила предварительного напряжения вызовет равномерное осевое напряжение, равное PT / A. в дополнение к осевому напряжению. применение PT в точке e вызовет напряжение изгиба (при сжатии) в нижнем волокне и напряжение изгиба (при растяжении) в верхнем волокне, как показано на рисунке ниже. в результате натяжение нижнего волокна будет уменьшено, а также уменьшится сжатие верхнего волокна.это приведет к члену с большей силой по сравнению с предыдущими случаями
Руководство по проектированию двутавровых балок из предварительно напряженного бетона и втулок TxGirder
Выбор типа моста
Выбор типа моста. Основным фактором при выборе типа моста в системе государственной помощи является первоначальная стоимость.Будущие расходы на техническое обслуживание, время строительства и местоположение учитываются при
Дополнительная информация
Электронное уведомление PENNDOT
Бюро электронных уведомлений PENNDOT Отдела проектирования и технологий мостов BRADD № 036 18 октября 2013 г. Выпуск BRADD версии 3.2.0.0 Очередной выпуск автоматизированного проектирования мостов
от PennDOT
Дополнительная информация
Опалубка для бетона
ВАШИНГТОНСКИЙ УНИВЕРСИТЕТ ДЕПАРТАМЕНТ УПРАВЛЕНИЯ СТРОИТЕЛЬСТВОМ CM 420 ВРЕМЕННЫЕ КОНСТРУКЦИИ Зимний квартал 2007 г. Профессор Камран М.Опалубка Nemati для проектирования горизонтальной и горизонтальной бетонной опалубки
Дополнительная информация
Двусторонняя конструкция с постнатяжением
Страница 1 из 9 Следующий пример иллюстрирует методы проектирования, представленные в ACI 318-05 и IBC 2003. Если не указано иное, все номера таблиц, рисунков и уравнений, на которые есть ссылки, взяты из этих книг.
Дополнительная информация
ГЕОМЕТРИЧЕСКИЙ ДИЗАЙН CIVL 3161
ГЕОМЕТРИЧЕСКИЙ ДИЗАЙН CIVL 3161 Задание для чтения: с.45-72 (4-е изд.) С.45-75 (предыдущее изд.) В учебнике Маннеринга. Геометрический дизайн дорожных сооружений учитывает пропорции физических элементов
.
Дополнительная информация
9.3 Двусторонние плиты (Часть I)
9.3 Двусторонние плиты (Часть I) В этом разделе рассматриваются следующие темы. Введение Анализ и конструктивные особенности при моделировании и анализе Распределение моментов по полосам 9.3.1 Введение Плиты
Дополнительная информация
Терминология Safe & Sound Bridge
Безопасный и надежный мост Терминология Абатмент Подпорная стена, поддерживающая концы моста и, в целом, удерживающая или поддерживающая насыпь на подходе.Подъезд Часть моста, по которой проходит
Дополнительная информация
ПРИМЕР КОНСТРУКЦИИ ПОДНОЖКИ
Графство: Любой Дизайн: BRG Дата: 10/007 Шоссе: Любой Ck Dsn: BRG Дата: 10/007 ПРИМЕР ДИЗАЙНА ПОДХОДОВ Дизайн: На основе спецификаций AASHTO LRFD 007, Руководства по проектированию мостов TxDOT LRFD и проекта TxDOT 0-4371
Дополнительная информация
Балка. Армирование. Проект 07.12.02
Проект армирования балок 12/7/02 1 УСИЛЕНИЕ СТРУЙ Целью данного пособия по проектированию CSD является предоставление процедур и предлагаемых деталей для армирования стальных балок с открытой стенкой.Есть три базовых
Дополнительная информация
16. Балочно-перекрытие.
ENDP311 Конструктивный бетонный дизайн 16. Конструкция из балок и перекрытий Система балок и перекрытий Как работает перекрытие? L-образные и тавровые балки Удерживающие балку и плиту вместе Школа гражданского строительства Университета Западной Австралии
Дополнительная информация
Раздел А Ферма крыши
Раздел A Типы фермы крыши Wisconsin Truss, Inc.можно строить фермы различных типов, ниже приведены некоторые распространенные примеры. Обычные ножницы для бобтейлов Mono Studio Dual Slope Cathedral Tray Vault Parallel
Дополнительная информация
CH. 2 НАГРУЗКИ НА ЗДАНИЯ
CH. 2 НАГРУЗКИ НА ЗДАНИЯ ГРАВИТАЦИОННЫЕ НАГРУЗКИ Собственные нагрузки Вертикальные нагрузки, связанные с весом здания и любого постоянного оборудования. Постоянные нагрузки на элементы конструкции не могут быть легко определены. B / c Вес зависит от
Дополнительная информация
Стальные балки и балки
НА СТАЛЬНОЙ КОНФЕРЕНЦИИ Советы по эффективному использованию балок Тим Холтерманн, С.E., P.E .; Дрю Поттс, ИП; Bob Sellers, P.E .; и Уолт Уортли, P.E. Надлежащая координация между инженерами-строителями и балкой
Дополнительная информация
КОНКУРС PCI BIG BEAM
КОНКУРС PCI BIG BEAM Официальные правила конкурса PCI Engineering Design Competition 2015/16 учебный год Комитет по образованию студентов PCI приглашает студентов принять участие в
.
Дополнительная информация
Камбер, недобрая кривая
Камбер, недоброжелательная кривая Поймите, как справиться с изгибом на типичной трубной мельнице: В.Б. Бад Грэм, автор статей. Хорошо, мы собирались поговорить о кривых. Не тот, что видели в игре с мячом, а
Дополнительная информация
ПРОДУКТ И ИНЖЕНЕРНОЕ РУКОВОДСТВО
СОДЕРЖАНИЕ Содержание … 1 Общая информация и технические характеристики мезонина … 2 Информация о плане мезонина SM0010PE … 3 Информация, необходимая для антресольных конструкций … 4 Этаж и / или антресоль
Дополнительная информация
TSL профессиональные услуги
Отчет для: Лаборатория №: 402876-05 5375 Эджуэй Драйв, АЛЛЕНДЕЙЛ, Мичиган, США Дата отчета: 21 декабря 2005 г. 49401 Дата получения: 3 ноября 2005 г. Телефон: 616 875 7725 Факс: 616 875 6009 Заказчик П.O. #: COD
Дополнительная информация
Глава 6 СИСТЕМЫ КРЫШИ-ПОТОЛКА
Глава 6 СИСТЕМЫ КРЫШИ-ПОТОЛКА В этой главе основное внимание уделяется системам крыши-потолка с деревянным каркасом. Холодногнутый стальной каркас для системы кровля-потолок также разрешен IRC, но не будет обсуждаться;
Дополнительная информация
ПРИМЕРЫ STRUSOFT ПРЕДНАПРЯЖЕНИЕ 6.4.
ПРИМЕРЫ ПРЕДНАПРЯЖЕНИЕ 6.4 ПОШАГОВЫЕ ПРИМЕРЫ 6.o4.oo5-2o14-o7-o18 Page 1 СОДЕРЖАНИЕ 1 БАЗОВАЯ КОНЦЕПЦИЯ 2 1.1 КОДЫ 2 1.2 ПЛАН ПРОГРАММЫ 3 1.3 ОГРАНИЧЕНИЯ В ТЕКУЩЕЙ ВЕРСИИ 3 2 ПРИМЕРЫ 4 2.1 МОДЕЛИРОВАНИЕ
Дополнительная информация
КРАТКОЕ ОПИСАНИЕ ГЛАВА 6
КРАТКОЕ ОПИСАНИЕ ГЛАВА 6 Настоящий отчет о развитии моста был подготовлен для документирования процесса принятия решений и рекомендаций по строительству моста, ведущего по бульвару Мейтленд (в восточном направлении) по шоссе I-4 под номером
.
Дополнительная информация
ГЛАВА 4 СИСТЕМЫ ДРЕНАЖНЫХ СИСТЕМ
ГЛАВА 4 ШТОРМОВЫЕ ДРЕНАЖНЫЕ СИСТЕМЫ 4.1 Обзор … 4-1 4.1.1 Введение … 4-1 4.1.2 Определение входного патрубка … 4-1 4.1.3 Критерии … 4-1 4.2 Дренаж дорожного покрытия … 4-2 4.2. 1 Введение … 4-2 4.2.2 Ливневой сток
Дополнительная информация
Системы ливневого дренажа 11.9-1
Системы ливневого дренажа 11.9-1 11.9 Расчет потока в водостоке 11.9.1 Введение Расчет потока в водостоке необходим для того, чтобы связать количество потока (Q) в ограниченном канале с разбросом
Дополнительная информация
Выбор профиля алюминиевых систем
Выбор профиля для алюминиевых систем Цель этого документа — кратко изложить способ выбора алюминиевого профиля на основе требований к прочности для каждого применения.Штора
Дополнительная информация
Вес балки
— Prestress Services Industries, LLC
Вес балки
Следующая таблица веса балок была разработана для всех текущих секций балок Prestress Services Industries LLC (PSI). Эти веса в расчете на один погонный фут оцениваются на основе ожидаемого фактического веса балки с бетоном обычного веса с добавлением 4% -ного запаса прочности и округлением в большую сторону до ближайшего приращения 5 фунтов.Окончательный вес указан на заводских чертежах PSI.
Коробчатые балки
| Раздел | Ширина | Ширина балки | ||||||
|---|---|---|---|---|---|---|---|---|
| 12 \ | 17 \ | 21 \ | 27 \ | 33 \ | 42 \ | 48 \ | ||
| B | 36 \ | 470 | 555 | 645 | 765 | 835 | 865 | НЕТ |
| 48 \ | 625 | 700 | 770 | 890 | 1005 | 1105 | 1225 | |
| CB | 36 \ | 470 | 565 | 600 | 785 | 815 | 935 | НЕТ |
| 48 \ | 625 | 700 | 800 | 920 | 1020 | 1120 | 1240 | |
Гибридные двутавровые балки WF (перемычка = 8 ″ — нижний фланец = 40 ″)
| Раздел | Верхний фланец | Глубина луча | ||||||
|---|---|---|---|---|---|---|---|---|
| 36 \ | 42 \ | 48 \ | 54 \ | 60 \ | 66 \ | 72 \ | ||
| HN | 49 \ | 955 | 1005 | 1060 | 1110 | 1160 | 1215 | 1265 |
| 61 \ | 1015 | 1065 | 1115 | 1170 | 1220 | 1275 | 1325 | |
Двутавровые балки, модифицированные AASHTO (перемычка = 8 ″ — нижний фланец = 26 ″)
| Раздел | Верхний фланец | Глубина луча | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 54 \ | 60 \ | 66 \ | 72 \ | 78 \ | 84 \ | 90 \ | 96 \ | 102 \ | ||
| 4J | 49 \ | 980 | 130 | 1080 | 1135 | 1185 | 1240 | 1290 | 1340 | 1395 |
| 61 \ | 1025 | 1075 | 1130 | 1180 | 1230 | 1285 | 1335 | 1390 | 1440 | |
| 4 мес. | 36 \ | 880 | 935 | 985 | 1040 | 1090 | 1140 | 1195 | 1245 | 1300 |
| 4N | 49 \ | 1025 | 1075 | 1125 | 1180 | 1230 | 1285 | 1335 | 1385 | 1440 |
| 61 \ | 1080 | 1135 | 1185 | 1235 | 1290 | 1340 | 1395 | 1445 | 1495 | |
AASHTO двутавр
| Раздел | Глубина | |
|---|---|---|
| 1I | 28 \ | 300 |
| 2I | 36 \ | 400 |
| 3I | 45 \ | 610 |
| 4I | 54 \ | 855 |
| I + 2 | 28 \ | 360 |
Тройник двутавровой балки Южных штатов
| Раздел | Верхний фланец | Глубина луча | ||
|---|---|---|---|---|
| 54 \ | 63 \ | 72 \ | ||
| BT | 42 \ | 715 | 775 | 835 |
Сплошная квадратная свая
| Раздел | Ширина / Глубина | |
| PI | 14 \ | 220 |
| 16 \ | 290 | |
| 18 \ | 365 | |
| 20 \ | 450 | |
| 24 \ | 645 |
Основы предварительно напряженного бетонного моста (с решенным примером)
Основы предварительно напряженного бетонного моста (с решенным примером)
Введение: В предварительно напряженном бетоне к бетонному элементу прилагается усилие предварительного напряжения, которое вызывает осевое сжатие, которое противодействует всем или частично растягивающим напряжениям, возникающим в элементе в результате приложенной нагрузки.В области мостостроения использование предварительно напряженного бетона способствовало строительству длиннопролетных бетонных мостов. Они часто состоят из сборных элементов, которые поднимаются на место, а затем натягиваются на уже установленные элементы, причем процесс продолжается до завершения пролета. Для небольших мостов использование предварительно напряженных железобетонных балок с простой опорой оказалось экономичной формой строительства. Введение диапазонов стандартного сечения балок упростило проектирование и строительство этих мостов. Методы предварительного напряжения:
1. Предварительное натяжение
Предварительное натяжение
2. Последующее натяжение
Последующее натяжение
Предельное состояние эксплуатационной пригодности
- В отличие от бетона Расчет предварительно напряженных железобетонных элементов изначально основан на их поведении при изгибе в условиях рабочей нагрузки.
- Затем проверяется предел прочности всех элементов на изгиб, сдвиг и кручение после того, как будут выполнены предельные состояния эксплуатационной пригодности.
- Основная функция предварительного напряжения заключается в обеспечении того, чтобы в бетоне возникали только ограниченные растягивающие напряжения во всех условиях в пределах рабочего диапазона нагрузок.
- Для соблюдения предельного состояния растрескивания необходимо соблюдать ограничения по напряжению для самых внешних волокон секции.
Ограничение напряжения BS8110
- Класс 1: Отсутствие растягивающих напряжений;
- Класс 2: напряжения при изгибе при растяжении, но без видимых трещин;
- Класс 3: напряжения при изгибе при растяжении, но ширина поверхностных трещин не превышает максимального значения (0.1 мм для стержней в агрессивных средах и 0,2 мм для всех остальных элементов)
Потери предварительного напряжения:
- Упругая деформация бетона
- Затяжка анкера
- Потери на трение
- Усадка бетона
- Ползучесть бетона
- Сталь
- релаксация
Общие потери предварительного напряжения: Если начальная сила предварительного напряжения, приложенная к элементу, равна Pi, то эффективная сила предварительного напряжения при перемещениях равна aPi, а при рабочей нагрузке — bPi.Значение a отражает краткосрочные потери из-за упругого укорочения, втягивания анкеров и трения. Общий коэффициент потерь b учитывает краткосрочные и долгосрочные зависящие от времени потери из-за усадки бетона, ползучести и релаксации стали. Диаграмма Магнеля Отношения между 1/ P i и e являются линейными, и если они построены графически, они предоставляют полезные средства для определения соответствующих значений P i и e . Эти диаграммы были впервые представлены бельгийским инженером Магнелем, отсюда и название Диаграмма Магнеля.Диаграмма магнеля
Зона кабеля и профиль кабеля
- После выбора силы предварительного напряжения на основе наиболее критического сечения можно определить пределы эксцентриситета e на других участках вдоль элемента.
- Производится допустимая кабельная зона, внутри которой профиль может принимать любую форму.
- Термин «трос» используется для обозначения результата всех отдельных жил.
- Пока «кабель» находится внутри зоны, напряжения на различных этапах нагружения не будут превышать допустимых значений, даже если некоторые из жилы могут физически находиться вне зоны кабеля.
Сдвиг в предварительно напряженной бетонной балке
- Сопротивление сдвигу предварительно напряженных бетонных элементов в предельном состоянии зависит от того, есть ли трещины в секции в области наибольшей силы сдвига.
- Режим отказа в двух случаях разный. Если секция не имеет трещин при изгибе, то разрушение при сдвиге инициируется трещинами, которые образуются в стенках двутавровых или тавровых секций после превышения основной прочности на разрыв.
- Если в секции есть трещины, то разрушение инициируется трещинами на растянутой поверхности элемента, выходящей в зону сжатия, аналогично режиму сдвига для железобетонных элементов.
Армирование сдвигу Если сопротивление сдвигу предварительно напряженного бетонного элемента недостаточно, то сдвиговое армирование должно быть выполнено в виде звеньев, подобных тем, которые используются в железобетонных элементах. Предел прочности предварительно напряженного бетона: После проектирования стержня с учетом ограничений по напряжению для эксплуатационной пригодности необходимо проверить его предельное состояние. Прогиб предварительно напряженных балок Прогиб предварительно напряженных балок трудно оценить на практике, поскольку он зависит от многих переменных, а именно:
- Упругое прогиб из-за предварительного напряжения
- Упругое прогиб из-за начальной нагрузки
- Ползучесть под постоянными напряжениями
- Прогиб из-за потери предварительного напряжения
- Дополнительный прогиб из-за временной нагрузки
Прогиб из-за предварительного напряжения можно рассчитать, рассматривая предварительное напряжение как эквивалентную нормальную нагрузку.Поскольку бетон деформируется как под нагрузкой, так и со временем из-за ползучести, прогиб бетонных конструкций следует оценивать как в краткосрочных, так и в долгосрочных условиях. Конец блок Дизайн
- Есть 2 проблемы, связанная с конечными блочной конструкцией, а именно, оценка разрывных растягивающих напряжений и сжимающий подшипник подчеркивают непосредственно под опорной плитой.
- Для элементов, подвергнутых последующему натяжению, предварительное напряжение в сухожилии передается через анкерные крепления в виде сосредоточенной силы.
- Согласно принципу Сен-Венана, распределение напряжений в элементе достаточно равномерно вдали от анкеровки, но в области самого анкерного крепления распределение напряжений сложное.
Составная конструкция:
- Многие области применения предварительно напряженного бетона включают сочетание сборных предварительно напряженных бетонных балок и монолитной железобетонной плиты.
- Типичным примером является заполнение на месте между сборными балками моста.Балки рассчитаны на то, чтобы действовать самостоятельно под действием собственного веса плюс вес влажного бетона плиты. После затвердевания бетона в плите, при условии наличия адекватного горизонтального сдвигового соединения между плитой и балкой, они ведут себя как составная секция под эксплуатационной нагрузкой. Балка действует как несъемная опалубка для перекрытия, которая обеспечивает сжатие полки составной секции.
- Таким образом, размер поперечного сечения балки может быть сведен к минимуму, поскольку компрессионный фланец требуется только на потолке при перемещении.Это приводит к использованию перевернутых Т-образных секций.
Полная тема раскрыта в форме презентации в PowerPoint, представленной ниже, вместе с решенным примером на мосту из бетонных плит с последующим натяжением.
PPT — Мониторинг предварительно напряженного бетонного моста с коробчатой балкой на предмет перегрузок Презентация в PowerPoint
Мониторинг предварительно напряженного бетонного моста с коробчатой балкой на предмет перегрузки Осман Хаг-Эльзафи Джонатан Кунин Структурные исследования Бюро исследований и развития транспорта Департамент транспорта штата Нью-Йорк
Обзор • Маршрут 9W над мостом Койманс-Крик • Перегрузка и схемы пересечения • План контрольно-измерительных приборов • Мониторинг перегрузок и сбор данных • Анализ данных и результаты • Выводы
Маршрут 9W над Койманс-Крик 45 Маршрут 9W над Coeymans Creek • Построен в 1985 г. • AADT из 26 000 автомобилей • Длина 107 футов • 11 смежных балок из предварительно напряженного железобетона • Балки шириной 8,4 фута • Балки шириной 3,3 фута (центральные балки) • Встроенные опоры • Настил из композитного бетона
Маршрут 9W через Койманс-Крик 9 0315 • Котельные модули для электростанции • Различный вес (от 83 до 253 тысяч фунтов) • Загрузка на 16-осные прицепы (123 тысячи фунтов) • Грузы, тянущие 1 или 2 тягача • 4-осные тягачи (46 тысяч фунтов) • 3-осные тягачи ( 77 тысяч фунтов) • Полная нагрузка до 453 тысяч фунтов
Маршрут 9W над Койманс-Крик Перегрузка
Маршрут 9W над Койманс-Крик Перекресток с перекладиной на перекрестке
9113 Диагональный перекресток
Перекресток
Маршрут 9W через Койманс-Крик • Цели проекта: • Измерение уровней напряжений в балках • Оценка двух схем пересечения • Изучение конструкции интегрального абатмента
Маршрут 9W над Койманс-Крик План
Маршрут 9W через Койманс-Крик 453 тысячи фунтов Перегрузка: Crossed Crabbed Midspan Strains
Маршрут 9W через Койманс-Крик 281 тысяча фунтов Перегрузка: перекрещенные по диагонали штаммы среднего пролета
Маршрут 9W над Койманс-Крик 453 тысяч фунтов Перегрузка: скрещенные коэффициенты распределения крабов
Маршрут 9W над Coeymans Factors
Маршрут 9W над Coeymans Factors
Распределение супервысоких линий
Маршрут 9W через Coeymans Creek Сравнение факторов распределения
Маршрут 9W над Coeymans Creek 453 кипов Перегрузка: Crossed Crabbed Beam 8 штаммов
Route 9Wrossed Beam Superload 11 Crossed Coeagon Штаммы
Маршрут 9W над Койманс-Крик • Были проведены дополнительные испытания под нагрузкой • Известны веса и конфигурации • Изучить распределение поперечной нагрузки • Проверить компьютерную программу • Для анализа использовался BRADD II
Маршрут 9W над Койманс-Крик Тес нагрузки t Грузовые автомобили: перекрестные прямые деформации промежуточного пролета
Маршрут 9W над Койманс-Крик Грузовые автомобили для испытаний под нагрузкой: перекрестные прямые коэффициенты распределения
Маршрут 9W над Койманс-Крик Влияние интегральных концевиков
Маршрут 9W над Coeymans Creek Выводы • Измеренные уровни напряжения показали, что балки не растрескались • Хорошее распределение поперечной нагрузки подтверждено нагрузочными испытаниями • Нет явного преимущества крабовой схемы перед диагональным пересечением • Модели распределения нагрузки были аналогичными
Маршрут 9W над Койманс-Крик Выводы • Мост действовал где-то между полностью фиксированным и просто поддерживаемым • Моменты действующей нагрузки варьировались от 52% до 66% от анализа с простой поддержкой • Выводы относятся к этому мосту и не может быть обобщен для всех st ructures
Контактная информация Осман Хаг-Эльсафи, Ph.

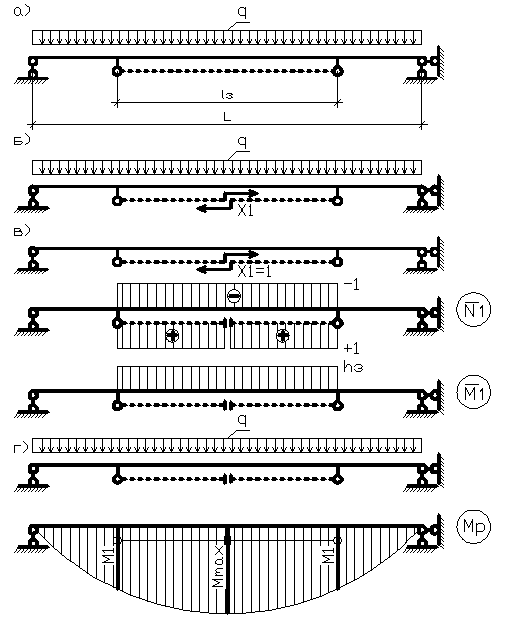 Расчетно-теоретический. 1960 г. Уманский А.А.
Расчетно-теоретический. 1960 г. Уманский А.А.