Расчет количества арматуры для плитного фундамента: Как рассчитать количество арматуры для монолитной плиты
- Калькулятор расчета количества дополнительной арматуры для плитного фундамента
- Расчет арматуры для монолитной плиты
- Как рассчитать арматуру на фундамент
- Калькулятор расчета фундаментной плиты: материалы, бетон, армирование
- Расчет фундаментной плиты, расчет плитного фундамента
- Калькулятор расчёта минимальной толщины прутьев для основного армирования плитного фундамента
- Калькулятор армирования бетона для перекрытий с нестандартной длиной
- (IUCr) Введение в расчет структурных факторов
- Расчет среднего и стандартного отклонения с помощью Excel
Калькулятор расчета количества дополнительной арматуры для плитного фундамента
Армирование фундаментной плиты толще 150 мм выполняется, как правило, в два яруса. А это означает, что необходимы те или иные дополнительные элементы конструкции, которые придадут каркасу требуемую объемность, обеспечат расположение верхней и нижней решеток на требуемом расстоянии и свяжут их между собой.
 Калькулятор расчета количества дополнительной арматуры для плитного фундамента
Калькулятор расчета количества дополнительной арматуры для плитного фундамента
Для этих дополнительных элементов обычно используется арматура меньшего диаметра и далее более низкого класса. Если для вязки основных поясов, верхней и нижней решетки должна применяться арматура класса не ниже A-III, диаметром 12 мм и более, то в данном случае есть возможность несколько сэкономить, используя пруты класса А-I или A-II, диаметром 8-10, а при не сильно нагружаемой плите – даже 6 мм. Но общий объем приобретения этого материала тоже может оказаться весьма внушительным – правильно определиться с этим поможет калькулятор расчета количества дополнительной арматуры для плитного фундамента.
Расчёт – несложен, но все же требует определенный пояснений, которые будут приведены ниже.
Калькулятор расчета количества дополнительной арматуры для плитного фундамента
Перейти к расчётам
Краткие пояснения по порядку проведения расчета
Итак, необходимо смонтировать две решётки основного армирования, а затем придать им правильное расположение друг относительно друга и связать между собой. Понятно, что диаметр арматурных прутьев и шаг их раскладки прутьев к этому времени уже рассчитаны.
Как рассчитать базовые характеристики армирующего каркаса плитного фундамента?
Нет ничего проще, если воспользоваться калькуляторами, размещенными на страницах нашего портала. Один из них поможет определиться с диаметром прутов и шагом их раскладки (размером ячейки решетки), а второй – подсчитает, какое количество арматуры для этого потребуется.
Теперь необходимо решетки увязать в единую каркасную конструкцию. Оптимальной видится схема, показанная на иллюстрации.
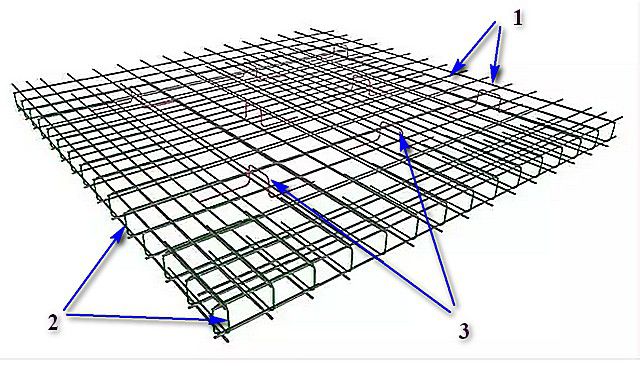 Проверенная схема качественного армирования фундаментной плиты
Проверенная схема качественного армирования фундаментной плиты
1 – продольные и поперечные прутья основных армирующих решеток.
2 – П-образные хомуты, которые связывают свободные концы симметрично расположенных прутьев верхней и нижней решеток. Такой подход, кроме всего прочего, дает еще и необходимое усиление каркаса как раз по линии будущего возведения несущих стен дома.
Для изготовления таких П-образных хомутов обычно берутся отрезки арматуры длиной 5×Н, где «Н» – это планируемая толщина фундаментной плиты.
3 – по всей площади плиты расставляются подставки, которые часто называют «пауками» или «лягушками».
 «Паук» или «лягушка» — подставка, которая будет обеспечивать необходимое расстояние между верхней и нижней решетками
«Паук» или «лягушка» — подставка, которая будет обеспечивать необходимое расстояние между верхней и нижней решетками
Размеры такой подставки принимают равными:
— нижние горизонтальные опоры – полтора шага решетки;
— верхняя «полка» — шаг решетки;
— высота зависит от планируемой толщины плиты с тем расчетом, что между ее краями и армирующими решётками должен оставаться просвет порядка 50 мм, чтобы слой застывшего бетона предохранял металла от коррозии.
— «плотность» установки подобных подставок – примерно две штуки на квадратный метр плиты.
Исходя из указанных соотношений, имея в распоряжении необходимые исходные данные, то есть размеры плиты и шаг решетки, несложно найти и необходимое количество арматуры для изготовления дополнительных элементов каркаса, с учетом 10-процентного запаса.
Результат дается в метрах, а также сразу пересчитывается в количество прутов стандартной длины – 11.7 или 6 метров.
Метры в тонны? – нет ничего проще!
Нередко возникает необходимость перевести количество стандартных прутов в килограммы или тонны. Для такого пересчета длины арматуры в весовой эквивалент воспользуйтесь специальным калькулятором, открыв его кликом по ссылке.
Как самостоятельно залить плитный фундамент?
Подробная информация о применении монолитного плитного фундамента, о его достоинствах и недостатках, о правилах расчета и технологии самостоятельного строительства – в специальной публикации нашего портала.
Расчет арматуры для монолитной плиты
Содержание статьи:
Монолитные плиты применяются, когда планируется отойти от стандартных параметров при строительстве и использовать особенные характеристики зданий.
Благодаря повышенной жесткости, использование монолитных плит является наиболее экономически выгодным вариантом. Единственный минус – монолитные плиты сложно укладывать при пониженных температурах.
Чтобы перекрытие было устойчивым и прочным и прослужило долгие годы, важно производить точный расчет монолитной конструкции, а если она заливается самостоятельно, то здесь не обойтись без расчета арматуры, которая является основой конструкции.
Во время создания составления проекта необходимо:
- определить марку бетона
- тип арматуры,
- просчитать схему ее укладывания,
- продумать систему изоляции от воздействия воды и тепла,
- подсчитать, сколько стройматериала необходимо для проведения работ.
Применение арматуры в строительных целях
Арматурные стержни в первую очередь служат для того, чтобы уберечь бетонное основание от значительных нагрузок и, как следствие, образования разрушений и трещин. Бетон сам по себе не может дать прочностные характеристики, особенно при большой площади использования, заливки.
В первую очередь арматура, стальная или композитная, позволяет фундаменту справляться с резкими скачками температур и подвижностью грунта. Здесь сразу становится актуальным информация о фундаменте на пучинистых грунтах, и о том, как именно его собирать и заливать.
В свою очередь, бетонное покрытие же спасает арматуру от плавления под воздействием огня и уберегает от коррозии, правда, последнее относится к стальному материалу, если же в работе используется современная стеклопластиковая арматура, то коррозия ей совершенно не страшна.
Неровная поверхность арматуры позволяет прочно сцепляться материалам при заливке бетонного раствора. Стержни арматуры укладываются продольно и поперечно для прочности всей конструкции. При этом укладку следует проводить по всем правилам.
Важно! Приступая к работе с армированием монолита, нужно понимать, как на практике реализовывается схема армирования.
Кроме того, необходимо выбрать способ соединения арматуры. Если это стальные стержни, то можно использовать и вязательную проволоку и сварку, если композитная, то проволоку.
Правила выбора арматуры
Перед тем, как подобрать материал, важно выяснить уровень планируемой нагрузки. Для этого выбирается фундамент и производится анализ грунта.
Далее производится расчет арматурного сечения. Для монолитной плиты выбирается диаметр стержней свыше 10 мм. При этом важно помнить о степени нагрузки на грунт.
При слабом грунте применяются более толстые арматурные стержни, к примеру, от 12 мм. Что касается углов строения, то здесь может быть использована и арматура до 16 мм.
Арматура бывает нескольких видов в зависимости от особенностей:
- Арматура продольного типа не позволяет растягиваться конструкции и появляться вертикальным трещинам. При воздействии арматурный стержень берет на себя часть нагрузки и равномерно распределяет по всей поверхности плиты.
- Арматура поперечного типа защищает от появления трещин в момент воздействия напряжения на опоры.
Расход арматуры при армировании
Обладая точными цифрами, можно правильно подобрать арматуру, толщину плиты, марку и количество бетона. Это в свою очередь позволит сэкономить силы и финансовые средства.
Напомним снова, как бы банально это не было, но не стоит экономить на покупке качественных стройматериалов, особенно, когда дело касается фундамента. В противном случае то может сказаться на сроке эксплуатации конструкции, и при ремонте потребуется выложить гораздо больше денег, чем было сэкономлено.
Существуют общепринятые нормы, как рассчитать расход арматурного материала в расчете на 1 кубометр бетонного раствора. При укладке арматура размещается вплотную на поверхности плиты, при этом от края остается 3-5 см.
Расчет на примере плиты 8х8
Точное количество арматуры рассчитывается на примере плиты размером 8х8 метров.
Для устойчивости грунта идеально подойдет стержень арматуры ∅ 10 мм. Как правило, сетка из арматуры выкладывается через шаг до 200 мм. Исходя из этого, не сложно вычислить нужное количество стержней.
Для этого ширина плиты делится на размер шага в метрах и прибавляется 1 прут (8/0,2+1=41). Для получения сетки стержни размещаются в перпендикулярном направлении. Значит, полученный результат нужно умножить на два (41х2=82 стержня).
Важно! При монтаже монолитной плиты требуется укладка двух слове сетки из арматуры сверху и снизу. Следовательно, данные снова умножаем на два (82х2=164 стержня).
Длина стандартного арматурного стержня составляет 6 метров. Исходя из этого, получается следующий расчет: 164х6=984 м.
Слои связаны между собой точками пересечения, количество которых легко вычислить, если количество стержней умножить на этот же показатель (41х41=1681 штук). Арматура в виде сетки укладывается в 5 см от основания плиты.
Толщина монолитной плиты равняется 200 мм. Чтобы произвести соединение, потребуется стержень длиной 0,1 метров.
Для осуществления всех соединений понадобится 0,1х1681=168,1 метров арматурного материала. Итого для проведения строительных работ потребуется 984+168,1=1152,1 метров арматуры, это теперь можно посчитать и в весе, если знать, сколько весит метр арматуры. Цифра получится также важной для расчета нагрузок на основания строения.
Практически всегда арматурные стержни продаются в строительных магазинах в килограммах. Один стержень весит в среднем 0,66 кг, значит, потребуется 0,66х1152,1=760 килограмм арматуры.
Как рассчитать арматуру на фундамент
 Как рассчитать, сколько арматуры пойдет на фундамент
Как рассчитать, сколько арматуры пойдет на фундамент
Армирование основания загородного дома является обязательном операцией, которую вы применяете в возведении объектов с огромной нагрузкой на фундамент. Каркас из металла, который помещен в тело бетона, будет воспринимать усилия на изгиб и растяжение, а также помогает равномерно распределить конструкционное напряжение, компенсировать деформации, а также уменьшать раскрытие трещин.
Но чтобы так и вышло, требуется знать, как рассчитать арматуру для ленточного фундамента, и лишь в этом случае можно получить поистине прочный фундамент.
Перед тем, как произвести расчеты, определите несущую способность грунтов по СНиПу 2.02.01-83. Это требуется, чтобы выяснить, какую максимальную степень нагрузки может выдерживать грунт. В соответствии с этим требуется выбирать конструктивное решение фундамента – столбчатое, ленточное, плитное или свайное.
Общие сведения
Расчет фундаментной арматуры
Для процесса армирования применяют гладкий и рифленый стальной прокат класса А500 или А400 – для рабочих стержней, А240 для элементов конструкции. Расчет требуется произвести по нормативам СНиП 52-01-2003 и актуализированным правилам СП 63.13330.2012 с учетом всех типов нагрузок, которые воздействуют на фундамент, а также виды оснований. Армирование производят плоскими или пространственными каркасами из поперечных, продольных и даже соединительных стержней. Вторые могут воспринимать нагрузку на растяжение по верхней поверхности, а также по подошве, вторые распределяют ее между вертикальными и горизонтальными элементами. Для устойчивости при изготовлении и установке применяют связки конструкции.
Основы расчетов для ленточного основания
Самым популярным видом основания в индивидуальном строительстве является монолитный ленточный. Он несложный в выстраивании, достаточно прочный и имеет необходимую степень жесткости. Его обустраивают в виде мелкоуглубленной или даже заглубленной конструкции. Особое значение для арматурного расчета на фундамент имеет глубина закладывания, действующие нагрузки и ширина рабочего сечения фундамента.
Как определить глубину закладывания
Подошвенную отметку выбирают в зависимости от типа грунта:
- При пылеватых, глинистых и мелкопесчаных грунтах фундамент требуется опирать на непромерзающий слой ниже, чем уровень грунтовых вод.
- При слабопучинистых и непучинистых грунтах подошвенная отметка не должна быть ниже, чем 50 см от верха имеющегося земельного уровня.
- Если есть подвал, то ленточное основание требуется углубить на 50 см ниже уровня пола, а столбчатое на 1.5 метра.
Разновидность грунта, положение УГВ и наличие слабых линз плывунов определяют посредством бурения или выкапывания шурфов. Глубина промерзания земли в разных регионах указана по СНиПу «Строительная климатология».
Сбор нагрузок
На данном этапе расчетов требуется просуммировать все разные нагрузки, действующие на основание:
- Нормативную нагрузку от снега.
- Воздействие от людей, предметов мебели, сантехнического оборудования, перегородок, которые есть внутри здания.
- Вес стен, крыши, плит перекрытия, пола и отделочных материалов.
- Собственный вес.
Вся информация будет содержаться в таблицах от СНиП 2.01.07-85 «Нагрузки и воздействия». Общую величину распределяют на погонные метры в ленточном основании, на число опор – в свайных или даже столбчатых.
Ширина подошвы
Рассчитать арматуру на фундамент очень важно. Ширина подошвы является величиной, которая помогает производить расчет арматуры на ленточное основание. При массивных кирпичных стенах применяют Т-образные ленты, свесы которых благодаря огромной площади опоры уменьшают грунтовое давление. Более легкие пенобетонные и каркасные строение выстраивают на основаниях с сечением прямоугольного типа. При расчете подошвенного размера требуется учесть предельное давление на землю и нагрузку от строения на несущие типы участков балок фундамента. В малоэтажном строительстве обычно применяют конструкции с шириной от 0.2 до 0.4 метров.
Подробности
Расчет ленточного фундамента
Для монолитных ленточных оснований загородных домов используют более простой метод расчета армирования по минимально допустимому арматурному сечению, которое воспринимает растягивающие усилия.
Порядок проведения расчета
По СНиПу общая площадь поперечного сечения стержней из стали должна быть не меньше 0.1% от рабочего сечения конструкции бетона. Найти это значение можно как произведение высоты сечения фундамента, которая равна глубине закладывания, умноженной на его ширину. Для продольного армирования применяют стержни с диаметром от 0.8 см. Найти нужное количество профилей круглого типа можно по специальной таблице, а значение требуется округлить в большую сторону. Есть также ограничения по минимальному размеру арматуры – на участках, где длина больше 3 метров, используют стержни с диаметром от 1.2 см. Требуемый арматурный метраж определяют по чертежам с размерами основания, причем запас должен быть в 5%. Массу требуется найти по таблицам стального сортамента.
Пример расчетов
Например, нужно произвести расчет армирования основания ленточного типа для загородного дом с размером 5*10 метров из блоков газосиликата. Глубина закладывания составляет 70 см, а ленточная ширина 40 см.
 Площадь сечения основания такова: 70*40=2800 см2.
Площадь сечения основания такова: 70*40=2800 см2.- Минимальная площадь (суммарная) для арматуры составляет 2800*0.01=2.8 см2.
- По таблице есть разные варианты – использовать 4 стержня с диаметром в 1 см, 3 штуки по 1.2 см или 2 прута с размером сечения 1.4 см.
- В нормативе указано, что при длине стороны больше, чем 3 метра, минимальный арматурный диаметр составляет 1.2 см. Чтобы распределение нагрузки от постройки было равномерным, требуется установить каркас из стали из двух сеток горизонтального типа, причем каждая из них будет иметь по два стержня с диаметром в 1.2 см.
- Арматуру поперечного типа требуется выбирать по высоте каркаса. Если она меньше, чем 0.8 метров, применяют проволоку для хомутов с диаметром в 0.6 см. Единовременно выполняются условия, при которых данный размер больше ¼ сечения продольных стержней.
- Содержание стали в метрах определяют по габаритам сооружения. Общая ленточная протяженность составляет 5+5+10+10=30 метров (если есть и несущая перегородка, то ее длину требуется просуммировать).
- Потребуется 4*30=12 п.м. арматуры с диаметром 1.2 см.
- Хомуты устанавливают с шагом в 0.4 метра, а их число 30/0.4=75 штук.
- Размер каждого (70*2+40*2)/1.15=191 см, причем 1.15 является коэффициентом для перевода периметра сечения в хомутную длину.
- Проволочная длина для соединительных элементов составляет 75*1.91=143.25 метра.
С учетом запаса в 5% на вязку и резку нужно:
- Арматура с диаметром 1.2 см 110*1.05=115.5 метров.
- Проволока с диаметром 0.6 см 143*1.05=150 метров.
Быстро и просто рассчитать арматуру на фундамент можно посредством онлайн калькуляторов, которые размещены на сайтах в Интернете. Весьма подробно о работе одного из особых приложений по расчету рассказывают в видеоинструкции.
Правила по армированию ленточного основания
Самым простым вариантом будет равномерно нагруженное основание на непросадочном непучинистом грунте. Подошва расположена выше, чем уровень промерзания и УГВ. В таком случае ширину фундамента требуется принимать равной толщине домовой стены. Армирование лишь конструктивное, и для подстраховки от непредвиденных замачиваний земли. Применяют рифленую или даже гладкую арматуру с диаметром от 0.8 до 1.2 см, поперечно связывают стержнями того же размера с сечением или меньшего с шагом в 0.3-0.4 метра. Вертикально в бетонном теле устанавливают противоусадочные вязаные или сварные сетки из проволоки малого диаметра (от 0.6 до 0.8 см) и с шагом не больше 0.2 метров. Другой случай – усиленная нагрузка на основание или более слабые земли. Форма ленточного сечения – в виде буквы Т в перевернутом виде. Армирование проводят тем же методом, но поперечные стержни можно рассчитать на давление от грунтового отпора. Оно способно разрушать подошву основания в 1.5 раза. Шаг монтажа хомутов не больше 0.2 метров, и их располагают под арматурой продольного типа, чтобы увеличивать высоту рабочего сечения. Третий вариант – это сочетать огромные нагрузки на фундамент и неблагоприятные условия грунта – наличия плывунов, пучинистости, карстов и высокого УГВ.
Чтобы не было проявления трещин и разрушения основания в результате грунтовой просадки. Армирование проводят по усиленному методу. Диаметр стержней составляет 1.2-1.6 см, а шаг не больше 0.2 метров. По подошве укладывают 1-2 ряда сеток, а в верхней части основания каркас сделан в виде балки. Через каждые 0.3-0.4 метра продольную арматуру требуется связать хомутами или прикрепить шпильками, чтобы зафиксировать ее пространственное положение.
Расчет основания свайного типа
Такие фундаменты представляют собой опоры, которые погружены в грунт (буронабивные или цельнометаллические), которые передают нагрузку от здания и соединенные по верху посредством деревянных, стальных или железобетонных ростверков. Такие основания применяют в частном строительстве:
- При строительстве каркасных или даже деревянных зданий с малой массой.
- При слабом грунте, где стальные основания выполнять невозможно – торфяники, сильнопучинистые влажные грунты или болота.
- В условиях со сложным рельефом- на овражистой или холмистой местности.
Минус, который может привести к удорожанию цены строительства – холодный цоколь и невозможность обустройства пола по земле. достоинство – отсутствие работ земляного типа. Сваи требуется вкручивать специальной буровой установкой или пробурить в земле отверстия с дальнейшим монтажом опалубки, бетонированием и армированием. При грунтах несыпучего типа раствор требуется заливать сразу в скважину. Схема расчета арматуры для буронабивного свайного фундамента.
 Определите тип грунта посредством ГОСТа «Грунты. Классификация».
Определите тип грунта посредством ГОСТа «Грунты. Классификация».- Рассчитайте временную и постоянную нагрузку (СНиП «Нагрузки и воздействия»).
- По ВСН 5-71 выберите несущую способность земли в зависимости от структуры.
- По сведениям найдите нагрузку на погонный метр ростверка, разделяя суммарную массу на общий периметр постройки.
- Определите несущую способность сваи.
Далее рассчитайте расстояние между опорами. Количество свай определите по расчетному расстоянию между опорами и размерами строений. Армируйте конструкции вертикальным каркасом из не меньше, чем четырех стержней с диаметром от 1 до 1.6 см с горизонтальной обвязкой из арматуры гладкого типа 0.6-0.8 см. По верху оставьте выпуски с длиной 0.25-0.3 метра.
Расчет армирования плитных оснований
Плитное армирование выбирают с учетом толщины. Если она менее 0.15 метров, укладывают одну сетку с ячейкой 0.2 метра, при огромном значении – 2. Каркас сварите из стержней с диаметром от 1.2 до 1.6 см, соедините с верхним слоем арматуры вертикальными хомутами с размером сечения до 1 см. Расчет плиты требуется выполнять по Своду Правил и «Руководству по проектированию фундаментов плитного типа». Он заключается в определении несущей способности по удельной нагрузке на землю и усилий изгиба. Ширина плиты основания больше размера дома на 0.1 метр. Для сетки арматуры определяют число стержней в обоих направлениях. Если применять два каркаса, то важно удвоить число прутиков. Чтобы найти, сколько требуется арматуры для соединений, определите число сочленений в сетке. Его важно умножить на длину хомута, которая равна толщине плиты за вычетом слоя защиты бетона. Далее можно рассчитать требуемое количество арматуры, закладывая запас в 5%. По сортаменту стали найдите ее вес.
Заключение
Основание является самой важной частью строительства. Неправильные расчеты могут привести к деформации и тресканью стен, а также разрушению всего здания в целом. Перед тем, как рассчитывать арматуру для основания, исследуют грунты на несущую способность и определят нагрузки на фундамент. По возможности такое дело лучше доверять профессионалам – траты на заказ таких услуг малы, а вот чувство уверенного стоит многого.
Калькулятор расчета фундаментной плиты: материалы, бетон, армирование
Инструкция для калькулятора фундаментной плиты


Одним из типов мелкозаглубленной основы для дома (с мелким заложением) считается фундаментная монолитная плита. Данный вид сооружения идеально подойдет под каркасные или деревянные дома, гаражи и бани, а также другие здания. Плитный фундамент относят по степени заложения в почву к мелкозаглубленному или незаглубленному сооружению.
В связи с невысокой глубиной заложения, такая основа для дома заглубляется всего на 0,4-0,5 метра, но встречаются моменты, когда частные постройки возводятся с цокольными этажами, в этом случае плитные фундаменты закладываются согласно проекту на расчетную глубину.
В отличие от столбчатых или незаглубленных ленточных каркасов, данный вид основы для дома характеризуется своей жесткой конструкцией.
Представленная онлайн программа-калькулятор может рассчитать
- Нужное количество стройматериалов для раствора: щебень, песок, цемент;
- Объем бетона для фундаментной плиты;
- Количество досок для обустройства опалубки;
- Примерную стоимость стройматериалов;
- Армирование монолитного сооружения (будет зависеть от геологических условий и типа проекта).
Вам необходимо указать все размеры в мм в колонке слева
X — Ширина плиты.
Y — Длина.
H — Высота.
W — Ширина секции (ячейки).
Z — Длина секции (ячейки).
R — Число горизонтальных рядов арматуры.
D — Диаметр арматуры.
В том случае, армирование не используется и данный расчет не требуется, то это поле можно не заполнять.
Для каждого отдельного случая требуется определенное количество цемента, чтобы изготовить 1 м³ бетона.
В первую очередь это будет зависеть от величины наполнителей и их пропорций, желаемой марки полученного раствора и используемой марки цемента.
K — Вес одного цементного мешка, выражается в килограммах.
M — Общее количество мешков с цементом для получения 1 м³ бетонной смеси.
L — Длина доски для опалубки.
T — Толщина.
H — Ширина.
Расчет материалов фундаментной плиты
- Стоимость строительных и сыпучих материалов может сильно варьировать в зависимости от сезона и района страны.
- Пересчитывать стоимость сыпучих материалов необходимо в цену не по объему, а по весу.
- Плита фундаментная — один из разновидностей мелкозаглубленного каркаса.
- Как правило, такая основа для дома выполнена в виде монолита из бетона, расположенного под площадью всей постройки.
- В обязательном порядке используется армирование по объему всего каркаса для устранения деформаций из-за нагрузок на плитный фундамент.
- Для создания несущей конструкции необходимо много арматуры и большой расход раствора, если сравнивать с классическими типами сооружений данного типа. В связи с этим плитный фундамент будет немного дороже, традиционных.
- Расчет объема бетона для правильной прочной заливки или армирующего прута, который используется для каркаса монолита, что позволит предотвратить перерасход вышеупомянутых строительных материалов.
Процесс армирования фундаментной плиты
- Как правило, для заливки монолитного плитного фундамента лучше всего применять бетон класса В и арматуру сечением от 12 до 16 миллиметров, категорически не рекомендуется экономить на этом.
- Армирование выполняется при помощи арматурных сеток, внизу и вверху плиты, которые перевязываются между собой. Это делается специально для того, чтобы получить прочное и жесткое основание, которое позволит выдерживать основе будущего дома любые нагрузки со стороны грунта или здания.
- Для того, чтобы правильно армировать горизонтальную плоскость монолита, нужно вязать сетку из армирующего прута с диаметром 12-16 мм и шагом 200 мм. Чтобы соединить прочно нижние и верхние секции, применяют арматуру диаметром 7-8 мм, которая вяжется с шагом 400х400 мм.
- Чтобы защитить арматурные пруты сверху и снизу, их нужно залить слоем раствора толщиной, как минимум 35 миллиметров.
Заливка монолитной конструкции
Для этого процесса, лучше всего использовать марку бетона М450. Также Вы должны быть уверенными, что Вам не доставят марку М350 и ниже. Класс раствора на прочность сжатия для плит фундаментных должен соответствовать марке В20 (М250), но не ниже. При этом водостойкость должна быть не менее W6. Заявленным критериям соответствуют бетона следующей марки — БСГ В 22,5 П3 F150 W6 и выше.
Для подачи раствора можно использовать лоток из миксера или бетонорукав. Раскидывать готовую смесь правильней всего с дальнего края опалубки. После этого начинаем бетонировать ближний край. В то время как выполняется заливка, один человек должен непрерывно обрабатывать заливку при помощи глубинного вибратора, что позволит получить равномерное распределение смеси по всему объему монолита, удалить воздушные пузырьки и выровнять ее поверхность.
Обязательно следующий день необходимо обильно полить всю поверхность монолитного сооружения водой. Если Вы заливку выполняли в жаркую погоду, то после этого процесса всю поверхность каркаса укрываем обязательно полиэтиленовой пленкой. Переходить к другим работам, можно в том случае, когда бетон набрал уже не менее 70% прочности. При температуре воздуха + 20 С для этого потребуется 7-10 дней. В том случае если температура +10 С и ниже, то следует выждать как минимум 20 дней.
Если ночная и дневная температуры имеют большой перепад, то лучше и правильней всего сориентироваться по среднесуточной температуре.
Теплоизоляция монолитной конструкции
Процесс теплоизоляции выполняется для того, чтобы защитить ее от внешних атмосферных влияний и холода, что позволит сэкономить на обогреве здания. Теплоизоляция фундаментного каркаса повышает темп
Расчет фундаментной плиты, расчет плитного фундамента
Расчет плитного фундамента, расчет монолитной плиты
Калькулятор плиты фундамента
Простой онлайн калькулятор расчета железобетонной плиты фундамента рассчитает точное количество стройматериалов для армированного монолитного фундамента. Начните расчет сейчас!
Устройство фундаментной плиты, железобетонная плита фундамента
Преимущество железобетонного плитного фундамента в возможности возводить его на любом грунте, особенно оправданно применения на движущихся грунтах и грунтах со слабыми несущими характеристиками, сильнопучинистых глиняных грунтах. Еще один плюс в дополнение к этому, материал строений можно выбрать любой, но чаще строят загородные дома и коттеджи имеющие в плане большую площадь или из тяжелых материалов, таких как кирпич или камень. Приятно то, что можно не ограничивать себя в размерах строения. А так же плита хорошо тепло изолируется и может являться черновым полом первого этажа.
Для армирования плиты выбирается арматура по ГОСТ 5781-32, диаметром 12 мм – 16 мм, класс бетона В30. Как рекомендуют профессионалы, для гидроизоляции лучше использовать мастику битумную горячего применения марка БН3 или более простой вариант — это толстая полиэтиленовая пленка.
Стоимость плиты фундамента
Единственным недостатком монолитной плиты является его высокая стоимость. При расчете плиты фундамента, очевидно, что устройство плитного фундамента связано с большими затратами прежде всего на бетон и арматуру, а также земляными работами. Кроме всего этого, при сложном ландшафте участка, если присутствует видимый перепад высот, потребуются дополнительные земляные работы по выравниванию участка, т.е. возвышенности срезают, низменности засыпают. Это все приводит к ощутимому удорожанию стоимости железобетонной фундаментной плиты. Все это вы можете проверить, произведя расчет стоимости фундамента плиты.
Калькулятор расчёта минимальной толщины прутьев для основного армирования плитного фундамента
Фундамент в виде монолитной плиты – это отличное решение, если состояние грунтов на участке строительства не позволяет применить наиболее распространенную ленточную схему. Равномерное распределение нагрузки на большой площади открывает возможности строительства основания без заглубления ниже уровня промерзания грунта, и при этом воздействия сил морозного пучения будут зданию не страшны. Вся система получается как бы «плавающей», повторяющей вертикальные сезонные подвижки грунта.
 Калькулятор расчёта минимальной толщины прутьев для основного армирования плитного фундамента
Калькулятор расчёта минимальной толщины прутьев для основного армирования плитного фундамента
Цены на арматуру
арматура
Понятно, что сама фундаментная плита будет испытывать весьма значительные разнонаправленные нагрузки, и ее целостность и надежность напрямую зависят от правильного армирования. Ниже расположен калькулятор расчёта минимальной толщины прутьев для основного армирования плитного фундамента – он поможет в вопросах предварительного планирования и самостоятельного составления проекта основания.
Несколько необходимых пояснений по проведению расчета приведены в соответствующем разделе публикации.
Калькулятор расчёта минимальной толщины прутьев для основного армирования плитного фундамента.
Перейти к расчётам
Краткие пояснения по порядку расчета
Расчет – несложен, и базируется на установленном СНиП нормативе, что суммарная площадь сечения арматурного пояса не должна быть менее 0,3% от площади сечения железобетонной конструкции.
- Предполагается, что пользователь знает линейные параметры будущей фундаментной плиты, определился с ее планируемой толщиной.
Как определить оптимальную толщину монолитной фундаментной плиты?
Этот размер подчиняется определенным правилам и зависит от множества исходных параметров. Провести самостоятельное вычисление оптимальной толщины фундамента-плиты поможет калькулятор, к которому ведет указанная ссылка.
- Армирование плиты осуществляется решетчатыми конструкциями с квадратными ячейками, увязываемых из арматурных прутьев класса A-III диаметром от 10 мм и выше. При этом если длина конструкции (стороны плиты) превышает 3 метра, то минимальный диаметр принимается не ниже 12 мм.
- При толщинах плиты 150 мм и меньше армирование осуществляется в один ярус, расположенный по центру. Если толщина больше (а так обычно и бывает) монтируется два яруса, с тем расчетом, чтобы каждый из них располагался не ближе 30, а лучше — 50 мм от верхнего или нижнего края плиты – чтобы тем самым образовался слой бетона, защищающий стальную арматуру от коррозии.
- Шаг расположения прутьев при увязке каркаса обычно лежит в диапазоне 200 ÷ 300 мм, с возможным варьированием, но и с соблюдением правила, что он в любом случае не должен превысить 1,5 толщины плиты.
- Так как ячейки армирующей решетки имеют квадратную форму, расчет может проводиться по любой из сторон фундаментной плиты.
- Калькулятор позволит проанализировать, какой диаметр арматуры будет выгоднее использовать – можно, варьируя шаг в допустимом диапазоне, отследить, как при этом изменяется и минимальный диаметр прута.
Как рассчитывается и возводится монолитный плитный фундамент?
Если у посетителя есть заинтересованность в самостоятельном обустройстве плитного фундамента, то ему стоит получить расширенную информацию из соответствующей публикации нашего портала.
Калькулятор армирования бетона для перекрытий с нестандартной длиной


Использование этого калькулятора зависит от максимальной длины стержней.
Если вы можете получить стержни длиной 60 футов, общая длина вашей плиты может составить 60 футов.
Если вы можете получить стержни длиной 40 футов, общая длина вашей плиты может составить 40 футов.
Если вы можете получить 20-футовые стержни, общая длина вашей плиты может составить 20 футов.
Если длина вашей плиты больше, чем длина стержня, вам придется соединить стержни (внахлест) вместе с помощью стяжной проволоки, чтобы получилась непрерывная длина.Необходимое количество нахлестов зависит от размера арматуры, используемого сорта, шага сетки, прочности бетона и того, что придумает ваш инженер, что он или она думает, каков минимальный отрезок, необходимый для выполнения вашего проекта.
Если «потребности» вашего проекта превышают требуемую максимальную длину стержня, вам придется добавить необходимое количество перекрытия к общей длине необходимой стержня, а также добавить немного для отходов.
Примечание:
Покупка арматуры большой длины нестандартной длины — не всегда самый дешевый вариант.
Даже с дополнительными линейными опорами, необходимыми для использования стандартного доступного размера 20-футового стержня для сращивания, стоимость этого может быть дешевле, чем покупка более длинных отрезков нестандартной длины.
Расчет
- Введите длину плиты
- Введите ширину плиты
- Введите требуемый шаг сетки ваших длинных стержней.
- Введите требуемый шаг сетки ваших транс-баров.
- Введите расстояние от края вашего первого стержня, обычно 2 дюйма.
- Введите расстояние, на котором длинные и короткие стержни должны заканчиваться от края.
Результаты
- Длина длинных стержней = длина длинных стержней.
- # Требуется длинная планка.
- Trans Bar Length = длина ваших стержней, идущих перпендикулярно длинным стержням.
- # необходимых длин транс-стержня.
- Общее количество арматуры, необходимой для линейных футов.
Приходите к нам по телефону 
Если у вас есть вопросы или комментарии, пожалуйста
Свяжитесь с нами
© 1998, VmNet..
(IUCr) Введение в расчет структурных факторов
S. C. Wallwork
В рентгеновской кристаллографии структурный фактор F ( hkl ) любого отражения рентгеновских лучей (дифрагированный луч) hkl — это величина, которая выражает как амплитуду, так и фазу этого отражения. Он играет центральную роль в решении и уточнении кристаллических структур, поскольку представляет величину, связанную с интенсивностью отражения, которая зависит от структуры, вызывающей это отражение, и не зависит от метода и условий наблюдения отражения.Набор структурных факторов для всех отражений hkl является первичными величинами, необходимыми для вывода трехмерного распределения электронной плотности, которое представляет собой изображение кристаллической структуры, рассчитанное методами Фурье. Это изображение является кристаллографическим аналогом изображения, сформированного в микроскопе путем рекомбинации лучей, рассеянных объектом. В микроскопе эта рекомбинация физически осуществляется линзами микроскопа, но в кристаллографии соответствующая рекомбинация дифрагированных лучей должна производиться математическим расчетом.
Способ, которым отдельные рассеянные или дифрагированные лучи объединяются для формирования изображения, зависит от трех факторов, связанных с каждым лучом:
- (a)
- направление,
- (b)
- амплитуда,
- ( в)
- фаза.
При физической рекомбинации лучей линзами микроскопа эти три части информации о каждом луче сохраняются и автоматически используются в процессе рекомбинации. В рентгеновской кристаллографии дифрагированные пучки наблюдаются отдельно, а их интенсивности измеряются как черные пятна на рентгеновской пленке или путем прямого квантового счета на дифрактометре.Путем определения индексов Миллера ( hkl ) плоскости кристалла, дающей начало каждому дифрагированному лучу, задается направление луча. По измеренной интенсивности пучка легко определить его амплитуду. Таким образом, известны две из трех необходимых частей информации о каждом луче, но, к сожалению, пока нет доступного метода для наблюдения фазы каждого дифрагированного луча, что является третьей частью информации, необходимой для того, чтобы математическая рекомбинация могла создать изображение структура.Это составляет так называемую фазовую проблему в кристаллографии.
Таким образом, решение кристаллической структуры состоит из применения некоторой техники для получения приблизительных фаз, по крайней мере, некоторых рентгеновских отражений, а процесс уточнения структуры — это процесс, при котором знание фаз распространяется на все отражения и сделан максимально точным для всех отражений. Помимо прямых методов получения некоторых начальных фаз, процессы решения и уточнения зависят от способности вычислять структурные факторы для предлагаемого приблизительного расположения некоторых или всех атомов в кристаллической структуре.Это тема данной брошюры. Видно, что можно одновременно рассчитать как амплитуду 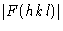 , так и фазу
, так и фазу 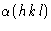 каждого луча, который будет дифрагировать на предлагаемой структуре. Поскольку фазы не могут быть сопоставлены с какими-либо наблюдаемыми величинами, справедливость предложенной структуры должна быть проверена путем сравнения расчетных значений амплитуд структурного фактора F c с наблюдаемыми амплитудами | Факс 0 |.Это выполняется путем вычисления коэффициента надежности или R , определяемого как
каждого луча, который будет дифрагировать на предлагаемой структуре. Поскольку фазы не могут быть сопоставлены с какими-либо наблюдаемыми величинами, справедливость предложенной структуры должна быть проверена путем сравнения расчетных значений амплитуд структурного фактора F c с наблюдаемыми амплитудами | Факс 0 |.Это выполняется путем вычисления коэффициента надежности или R , определяемого как
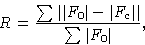
, где суммирование обычно проводится по всем отражениям, дающим значительные интенсивности. Из-за случайных ошибок в наблюдаемых амплитудах структурных факторов | F 0 |, и приближения, сделанные в модели, на которой основаны расчетные структурные факторы, никогда не смогут получить набор | F c | которые точно воспроизводят | F 0 |, поэтому уточнение структуры никогда не уменьшает R до нуля.Для качественных данных дифрактометра значения R в районе 0,05 являются обычными для полностью уточненных структур. Для начальных приблизительных структур, возникающих в процессе структурного решения, R , как правило, не должно быть больше примерно 0,5, чтобы можно было удовлетворительно уточнять.
Структурный фактор представляет собой результирующую рассеивающую способность рентгеновских лучей всей кристаллической структуры, однако, поскольку вся структура состоит из большого количества элементарных ячеек, все рассеянные в фазе друг с другом, результирующая рассеивающая способность фактически рассчитывается для содержания только одной элементарной ячейки.Таким образом, структурный фактор представляет собой результирующую амплитуду и фазу рассеяния всего распределения электронной плотности одной элементарной ячейки. Амплитуда рассчитывается как во сколько раз больше амплитуды рассеяния от изолированного электрона. Фаза вычисляется относительно фазы нуля для гипотетического рассеяния точкой в начале координат элементарной ячейки. Результирующая величина рассчитывается как наложение волн, по одной от каждого атома в элементарной ячейке, каждая волна имеет амплитуду, которая зависит от количества электронов в атоме, и фазу, которая зависит от положения атома в элементарной ячейке.
Прежде чем подробно рассмотреть, как выполнить этот расчет, мы должны сначала увидеть, как можно комбинировать волновые движения разных амплитуд и фаз. Мы рассматриваем простейший случай сложения волны амплитуды f 1 и фазы 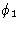 и волны амплитуды f 2 и фазы
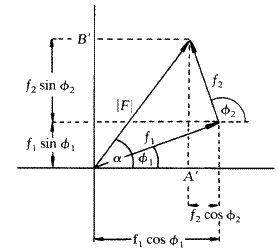
и волны амплитуды f 2 и фазы 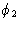 . Каждую волну можно рассматривать как функцию косинуса, генерируемую путем проецирования на горизонтальный диаметр окружности — положение точки ( P 1 или P 2 ), вращающейся с постоянной скоростью вокруг окружности, (Рис.1). Смещение выступа по горизонтальному диаметру можно принять равным x . Если бы каждая волна имела нулевую фазу, радиус, соединяющий точки P 1 или P 2 с центром каждого круга, составлял бы тот же угол
. Каждую волну можно рассматривать как функцию косинуса, генерируемую путем проецирования на горизонтальный диаметр окружности — положение точки ( P 1 или P 2 ), вращающейся с постоянной скоростью вокруг окружности, (Рис.1). Смещение выступа по горизонтальному диаметру можно принять равным x . Если бы каждая волна имела нулевую фазу, радиус, соединяющий точки P 1 или P 2 с центром каждого круга, составлял бы тот же угол 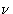 с горизонтальным диаметром в один и тот же момент времени, как показано на рис. 1 ( a ), а смещения по горизонтальным диаметрам будут заданы следующим образом:
с горизонтальным диаметром в один и тот же момент времени, как показано на рис. 1 ( a ), а смещения по горизонтальным диаметрам будут заданы следующим образом:

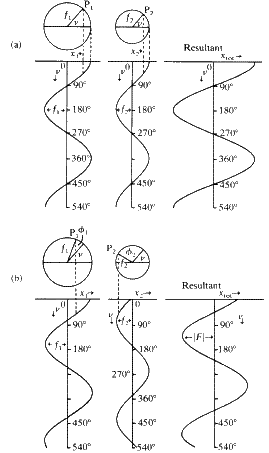 |
Сумма этих двух волновых движений представляет собой просто волну одной фазы с амплитудой ( f 1 + f 2 ). В любой момент времени полное смещение определяется как:
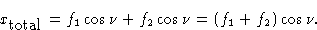
Когда первая волна имеет фазовый угол 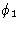 относительно радиуса под углом
относительно радиуса под углом 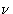 , а вторая волна имеет фазовый угол
, а вторая волна имеет фазовый угол 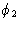 относительно того же радиуса, двухкомпонентные волны и их равнодействующая показаны на рис.1 ( б ). Результирующая теперь имеет амплитуду, которая меньше чем ( f 1 + f 2 ), потому что составляющие волны больше не полностью усиливают друг друга, и ее фаза отличается от фазы любого из компонентов. Смещения x 1 и x 2 для двух составляющих волн теперь задаются как:
относительно того же радиуса, двухкомпонентные волны и их равнодействующая показаны на рис.1 ( б ). Результирующая теперь имеет амплитуду, которая меньше чем ( f 1 + f 2 ), потому что составляющие волны больше не полностью усиливают друг друга, и ее фаза отличается от фазы любого из компонентов. Смещения x 1 и x 2 для двух составляющих волн теперь задаются как:
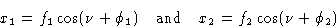
, а смещение для результирующей волны задается как
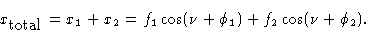
Когда косинусные члены расширяются, это становится
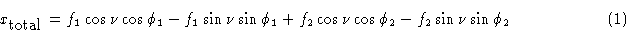

Как видно из рис.1 результирующая волна является другой косинусоидальной волной той же частоты, что и составляющие волны, но другой фазы, которую мы назовем 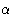 . Следовательно, его можно представить как:
. Следовательно, его можно представить как:
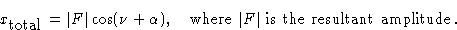
Расширяя это, мы имеем
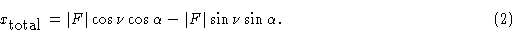
Сравнивая уравнение (2) с уравнением (1), мы видим, что
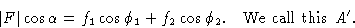
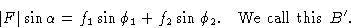
Чтобы найти амплитуду | F | и фаза 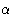 результирующей волны, мы отмечаем, что:
результирующей волны, мы отмечаем, что:
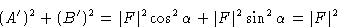
и
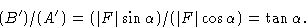
В общем, чтобы найти результирующую амплитуду и фазу для волны, состоящей из n косинусоидальных волн, из которых типичная составляющая j имеет амплитуда f j и фаза 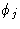 , имеем
, имеем


и | F | и 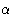 относятся к A ‘и B ‘, как и в случае двух компонентов.
относятся к A ‘и B ‘, как и в случае двух компонентов.
Это добавление компонентов может быть удобно представлено на векторной диаграмме, как на фиг. 2, где снова показан пример сложения тех же двух компонентов. На этой диаграмме можно увидеть, что A ‘- это алгебраическая сумма 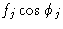 членов, а B ‘ — алгебраическая сумма
членов, а B ‘ — алгебраическая сумма 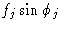 членов. Результирующий вектор F представляет собой векторную сумму двух компонентов и квадрат ее амплитуды, | F 2 |, по теореме Пифагора определяется выражением ( A ‘) 2 + ( B ‘) 2 .Направление или фаза результирующего задается углом
членов. Результирующий вектор F представляет собой векторную сумму двух компонентов и квадрат ее амплитуды, | F 2 |, по теореме Пифагора определяется выражением ( A ‘) 2 + ( B ‘) 2 .Направление или фаза результирующего задается углом 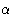 , тангенс которого равен B ‘/ A ‘.
, тангенс которого равен B ‘/ A ‘.
 |
Обычно амплитуду и фазу волны представляют комплексным числом, которое может быть выражено в форме a + ib или 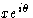
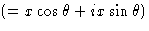 .В этих представлениях , или
.В этих представлениях , или 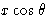 — действительная часть комплексного числа, а ib или
— действительная часть комплексного числа, а ib или 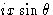 — мнимая часть. Это вполне согласуется с векторным представлением на рис. 2 в том, что A ‘представляет собой действительную часть a комплексной волны F , а iB ‘ является мнимой частью ib . Таким образом, горизонтальную ось на рис. 2 следует рассматривать как действительную ось, а вертикальную ось — как мнимую ось традиционной диаграммы Аргана для представления комплексных чисел.В экспоненциальной форме комплексной волны
— мнимая часть. Это вполне согласуется с векторным представлением на рис. 2 в том, что A ‘представляет собой действительную часть a комплексной волны F , а iB ‘ является мнимой частью ib . Таким образом, горизонтальную ось на рис. 2 следует рассматривать как действительную ось, а вертикальную ось — как мнимую ось традиционной диаграммы Аргана для представления комплексных чисел.В экспоненциальной форме комплексной волны 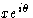 угол
угол 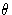 соответствует фазовому углу
соответствует фазовому углу 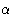 на фиг. 2, а x соответствует амплитуде | F |.
на фиг. 2, а x соответствует амплитуде | F |.
Увидев, как волны могут быть добавлены для получения результирующей волны, теперь мы можем применить эту процедуру к суммированию волн, рассеянных различными атомами элементарной ячейки, чтобы получить результирующий структурный фактор F . Нам необходимо рассмотреть амплитуду f рассеяния от каждого атома и его фазу 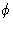 .Обе эти величины лучше всего подходят с точки зрения брэгговской трактовки дифракции рентгеновских лучей, которая будет описана вначале.
.Обе эти величины лучше всего подходят с точки зрения брэгговской трактовки дифракции рентгеновских лучей, которая будет описана вначале.
Брэгги, отец и сын, считали, что дифракцию рентгеновских лучей на кристалле удобнее рассматривать в терминах отражения от равномерно расположенных параллельных плоскостей в кристалле. Как и любой процесс отражения, угол 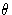 между падающим лучом и отражающей плоскостью равен углу между отраженным лучом и плоскостью.Однако, в отличие от зеркального отражения, только определенные углы падения и отражения вызывают заметную интенсивность отраженного луча. Это углы, при которых лучи, отраженные последовательными плоскостями кристалла, различаются по фазе на целый ряд длин волн. (Это ограничение возникает из-за того, что на самом деле проблема заключается в дифракции.) Разница в фазе находится путем вычисления разницы в длине пути для двух последовательных лучей.
между падающим лучом и отражающей плоскостью равен углу между отраженным лучом и плоскостью.Однако, в отличие от зеркального отражения, только определенные углы падения и отражения вызывают заметную интенсивность отраженного луча. Это углы, при которых лучи, отраженные последовательными плоскостями кристалла, различаются по фазе на целый ряд длин волн. (Это ограничение возникает из-за того, что на самом деле проблема заключается в дифракции.) Разница в фазе находится путем вычисления разницы в длине пути для двух последовательных лучей.
Рассмотрим первые два луча падающего луча, которые попадают в последовательные плоскости кристалла в точках O и B соответственно, где OB перпендикулярно плоскостям кристалла (рис.3 а ). Дополнительное расстояние, пройденное нижним лучом, вычисляется путем рисования перпендикулярных волновых фронтов OA и OC падающему и дифрагированному лучам соответственно. Видно, что это AB + BC . Поскольку 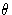 — это угол между AB и плоскостью кристалла и между BC и плоскостью кристалла,
— это угол между AB и плоскостью кристалла и между BC и плоскостью кристалла, 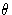 также является углом между перпендикуляром к AB (т.е. OA ) или к BC (т.е.е. OC ) и перпендикулярно плоскостям кристалла (т.е. OB ). Это показано на увеличенной части диаграммы на рис. 3 b . Теперь из треугольников ABO и BCO :
также является углом между перпендикуляром к AB (т.е. OA ) или к BC (т.е.е. OC ) и перпендикулярно плоскостям кристалла (т.е. OB ). Это показано на увеличенной части диаграммы на рис. 3 b . Теперь из треугольников ABO и BCO :
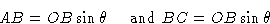

, так как OB = d , перпендикулярное расстояние между кристаллическими плоскостями. Таким образом, общая разница в пути между двумя лучами ( AB + BC ) равна 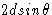 . Для усиления последовательных лучей эта разность хода должна составлять целое число длин волн.
. Для усиления последовательных лучей эта разность хода должна составлять целое число длин волн.

Это известно как уравнение Брэгга или закон Брэгга.
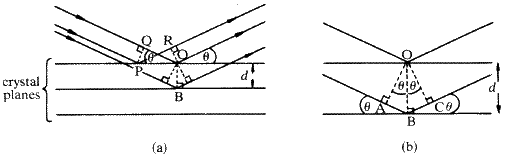 |
Во-вторых, мы должны показать, что разница в пути одинакова для двух лучей, отраженных от двух последовательных плоскостей кристалла, независимо от точек на плоскостях, в которых они падают на плоскости.Рассмотрим два луча, отраженные от верхней плоскости в точках P и O . Чтобы проверить, нет ли разницы в пути между этими двумя лучами, мы построим перпендикуляры PQ и OR . Расстояние, проходимое лучом, отраженным от O между перпендикулярными волновыми фронтами PQ и OR , составляет QO . Это равно 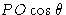 . Расстояние, пройденное лучом, отраженным от P между теми же двумя волновыми фронтами, составляет PR .Однако, поскольку угол RPO также равен
. Расстояние, пройденное лучом, отраженным от P между теми же двумя волновыми фронтами, составляет PR .Однако, поскольку угол RPO также равен 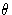 , PR также равен
, PR также равен 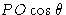 . Таким образом, два луча находятся в фазе друг с другом. Это также означает, что если разность фаз между лучами, отраженными на O и B , составляет
. Таким образом, два луча находятся в фазе друг с другом. Это также означает, что если разность фаз между лучами, отраженными на O и B , составляет 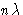 после отражения, то разность фаз между лучами, отраженными на P и B , также будет
после отражения, то разность фаз между лучами, отраженными на P и B , также будет 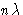 после отражения. Это устанавливает принцип, согласно которому разность фаз между лучами, отраженными от параллельных плоскостей в кристалле, зависит от расстояний до точек отражения, измеренных перпендикулярно плоскостям, а не от расстояния между точками отражения, измеренных параллельно плоскостям.Этот принцип используется как при рассмотрении того, как амплитуда рассеяния атома зависит от угла Брэгга
после отражения. Это устанавливает принцип, согласно которому разность фаз между лучами, отраженными от параллельных плоскостей в кристалле, зависит от расстояний до точек отражения, измеренных перпендикулярно плоскостям, а не от расстояния между точками отражения, измеренных параллельно плоскостям.Этот принцип используется как при рассмотрении того, как амплитуда рассеяния атома зависит от угла Брэгга 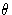 , так и при вычислении зависимости фазы рассеянного пучка от каждого атома от его положения в элементарной ячейке.
, так и при вычислении зависимости фазы рассеянного пучка от каждого атома от его положения в элементарной ячейке.
Если бы все электроны в атоме были сосредоточены в одной точке, амплитуда рентгеновских лучей, рассеянных атомом, была бы просто в Z раз больше амплитуды, рассеянной одним свободным электроном, где Z — атомный номер атома.Фактически, электроны образуют диффузное облако различной плотности, сферическое по симметрии в первом приближении, но с довольно высокой плотностью электронов, скажем, на расстоянии половины обычного атомного радиуса от центра атома. Рентгеновские лучи, рассеянные от одной части атома, могут быть не в фазе с рассеянными от другой части, так что их вклады в общее рассеяние сокращаются, а не складываются. Таким образом, полная амплитуда рассеяния атомом будет, как правило, меньше Z и будет зависеть от расстояния между параллельными дифракционными плоскостями для рассматриваемого отражения рентгеновских лучей.
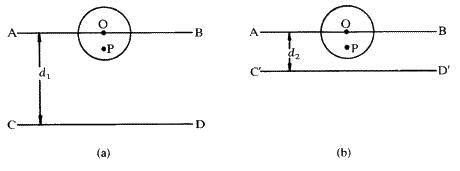 |
Это можно понять, обратившись к рис. 4. Слева показана ситуация, когда расстояние d 1 между плоскостями Брэгга AB и CD является большим по сравнению с атомом с центром в O .Если рентгеновские лучи, отраженные на CD , на одну длину волны не совпадают по фазе с рентгеновскими лучами, отраженными на AB , то луч, отраженный от P , будет только на небольшую часть длины волны не в фазе с отраженным лучом. с О . Следовательно, рассеянные лучи из этих двух точек будут в значительной степени усиливать друг друга. Фактически, рассеяние от всех частей атома будет в значительной степени складываться, давая общую амплитуду f не намного меньше, чем Z .На рис.4 ( b ), с другой стороны, рассматривается другое отражение рентгеновских лучей, где расстояние между плоскостями Брэгга, d 2 , теперь того же порядка размера, что и атом . Теперь луч, отраженный от точки P , будет почти точно не в фазе с лучом, отраженным от точки O . Между ними будет деструктивная интерференция (однако не сводя к нулю, потому что плотность электронов и, следовательно, амплитуда рассеяния при P будет меньше, чем при O ).В этой ситуации полная амплитуда рассеяния f от всего атома будет намного меньше Z . Поскольку d и угол Брэгга 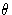 связаны уравнением Брэгга (5), ситуация на фиг.4 ( a ) соответствует отражению под малым углом
связаны уравнением Брэгга (5), ситуация на фиг.4 ( a ) соответствует отражению под малым углом 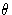 , а ситуация на фиг.4 ( b ) ) соответствует большому углу Брэгга
, а ситуация на фиг.4 ( b ) ) соответствует большому углу Брэгга 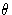 . Фактически, амплитуда рассеяния на атоме f плавно изменяется с
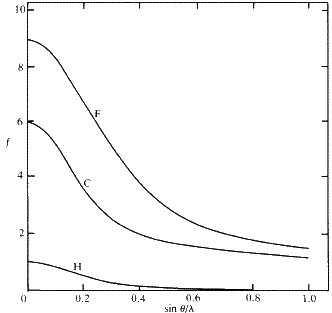
. Фактически, амплитуда рассеяния на атоме f плавно изменяется с 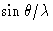 , как показано для некоторых типичных атомов на рис.5. Амплитуда f для атома называется атомным фактором рассеяния. Он экстраполируется на Z , поскольку
, как показано для некоторых типичных атомов на рис.5. Амплитуда f для атома называется атомным фактором рассеяния. Он экстраполируется на Z , поскольку 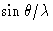 стремится к нулю, потому что d стремится к бесконечности, а разности фаз рассеяния от разных частей атомов стремятся к нулю. При вычислении структурного фактора для конкретного отражения рентгеновских лучей hkl расчет в первую очередь выполняется так, как если бы рассеяние для каждого атома происходило из одной точки — атомного центра. Влияние распределения электронной плотности по значительному объему затем учитывается путем умножения члена для каждого атома на атомный коэффициент рассеяния f , соответствующий углу Брэгга
стремится к нулю, потому что d стремится к бесконечности, а разности фаз рассеяния от разных частей атомов стремятся к нулю. При вычислении структурного фактора для конкретного отражения рентгеновских лучей hkl расчет в первую очередь выполняется так, как если бы рассеяние для каждого атома происходило из одной точки — атомного центра. Влияние распределения электронной плотности по значительному объему затем учитывается путем умножения члена для каждого атома на атомный коэффициент рассеяния f , соответствующий углу Брэгга 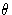 отражения.
отражения.
 |
Теперь мы должны рассмотреть, как фаза 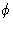 рассеяния на атоме как вклад в общий структурный фактор F зависит от положения атома в элементарной ячейке. Принцип метода заключается в том, что лучи, отраженные последовательными плоскостями Брэгга, имеют фазу на одну длину волны, отличную друг от друга, и поэтому их фазовый угол различается на
рассеяния на атоме как вклад в общий структурный фактор F зависит от положения атома в элементарной ячейке. Принцип метода заключается в том, что лучи, отраженные последовательными плоскостями Брэгга, имеют фазу на одну длину волны, отличную друг от друга, и поэтому их фазовый угол различается на 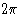 радиан или 360
радиан или 360 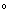 .Гипотетический луч, отраженный от начала координат ячейки, всегда определяет нулевой фазовый угол, поэтому точки пересечения плоскости hkl с осями ячейки соответствуют фазе
.Гипотетический луч, отраженный от начала координат ячейки, всегда определяет нулевой фазовый угол, поэтому точки пересечения плоскости hkl с осями ячейки соответствуют фазе 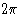 радиан или 360
радиан или 360 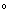 . Фаза для рассеяния любым атомом в элементарной ячейке (рассматриваемой для этой цели как находящаяся в точке своего центра) поэтому определяется его расстоянием, измеренным перпендикулярно между плоскостью, проходящей через начало координат, параллельной плоскости hkl , и плоскостью гкл сама.(Следует помнить, что фаза не зависит от положения, параллельного плоскостям Брэгга.) Расчет фазы лучше всего проиллюстрировать в двух измерениях, как на рис. 6.
. Фаза для рассеяния любым атомом в элементарной ячейке (рассматриваемой для этой цели как находящаяся в точке своего центра) поэтому определяется его расстоянием, измеренным перпендикулярно между плоскостью, проходящей через начало координат, параллельной плоскости hkl , и плоскостью гкл сама.(Следует помнить, что фаза не зависит от положения, параллельного плоскостям Брэгга.) Расчет фазы лучше всего проиллюстрировать в двух измерениях, как на рис. 6.
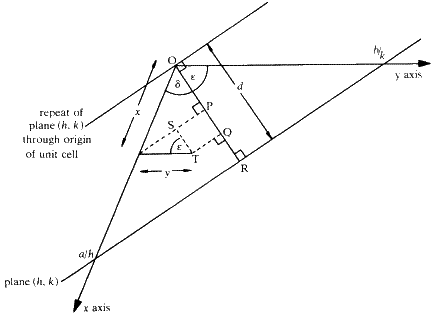 |
Оси x и y двумерной ячейки показаны пересеченными плоскостью Брэгга (фактически линией), определенной индексами Миллера h , k .Из определения индексов Миллера, пересечение по оси x происходит на расстоянии a / h от начала координат O , а пересечение по оси y происходит на b / k где a и b — размеры элементарной ячейки по осям x и y соответственно. Расстояние по перпендикуляру d между этой плоскостью и параллельной плоскостью через начало координат определяется расстоянием OR .Рассмотрим атом в точке T , имеющий координаты x и y в ячейке. Мы хотим знать, как далеко T перпендикулярно плоскости через O к плоскости через a / h , b / k , по сравнению с общим перпендикулярным расстоянием между этими плоскостями. Удобно измерять все перпендикулярные расстояния по линии ИЛИ , поэтому составляющая расстояния по координате x получается путем проецирования расстояния x на OR как OP , а составляющая из-за y координата получается путем проецирования y на OR как PQ .Общее перпендикулярное расстояние T от плоскости через O , следовательно, составляет OQ , и оно рассчитывается следующим образом:
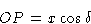
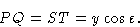
Но, из треугольника, определенного как O , R и точка a / h ,
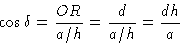
и из треугольника, определяемого O , R и точка b / k ,
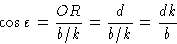
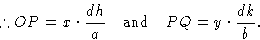
So
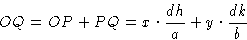
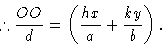
Теперь OR или расстояние d соответствует изменению фазы на 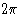 радиан.Таким образом, OQ соответствует изменению фазы на
радиан.Таким образом, OQ соответствует изменению фазы на 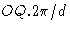 радиан. Следовательно, это равно
радиан. Следовательно, это равно 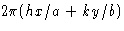 радиан и представляет собой фазу рассеяния от точки T по сравнению с нулевой фазой в начале координат ячейки.
радиан и представляет собой фазу рассеяния от точки T по сравнению с нулевой фазой в начале координат ячейки.
Когда это вычисление распространяется на три измерения, пересечение плоскости hkl с кристаллографической осью z в точке c / l и проекция z на перпендикуляр от O к самолету также необходимо учитывать.Фаза рассеяния атомом в точке x , y , z тогда задается формулой
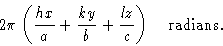
Таким образом, это выражение для рассчитанного фазового угла 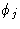 для использования в уравнениях, таких как (3) и (4). Амплитуда f j для рассеяния атома, которая учитывает количество электронов в атоме и тот факт, что они фактически не сконцентрированы в точке x , y , z , но распределенный вокруг него, является уже обсуждавшимся атомным фактором рассеяния f .Уравнения для действительной части ( A ‘) и мнимой части ( B ‘) структурного фактора, соответствующие уравнениям (3) и (4), таким образом:
для использования в уравнениях, таких как (3) и (4). Амплитуда f j для рассеяния атома, которая учитывает количество электронов в атоме и тот факт, что они фактически не сконцентрированы в точке x , y , z , но распределенный вокруг него, является уже обсуждавшимся атомным фактором рассеяния f .Уравнения для действительной части ( A ‘) и мнимой части ( B ‘) структурного фактора, соответствующие уравнениям (3) и (4), таким образом:
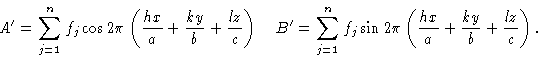
Или, в экспоненциальной форме, структурный фактор может быть выражен как:
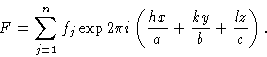
В каждом случае суммирование проводится по n атомов в элементарной ячейке.
На практике любой один атом в элементарной ячейке связан с другими атомами в ячейке за счет действия различных элементов симметрии.Принимая во внимание взаимосвязь между координатами этих связанных с симметрией атомов, можно вывести формулы, выражающие сумму факторов 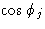 и сумму факторов
и сумму факторов 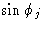 для всей этой группы связанных с симметрией атомов. Эти суммы обычно называются A и B соответственно. Вся сумма, A или B , затем умножается на коэффициент атомного рассеяния, который опять же на практике корректируется с учетом теплового движения атомов, которое еще больше размывает электронное облако и вызывает более быстрое падение f. j с
для всей этой группы связанных с симметрией атомов. Эти суммы обычно называются A и B соответственно. Вся сумма, A или B , затем умножается на коэффициент атомного рассеяния, который опять же на практике корректируется с учетом теплового движения атомов, которое еще больше размывает электронное облако и вызывает более быстрое падение f. j с 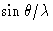 , чем показано на рис.5. Затем:
, чем показано на рис.5. Затем:
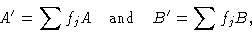
, где сумма берется только по атомам одной асимметричной единицы. Подробное описание этих расширений основных принципов расчета структурных факторов выходит за рамки данной брошюры, но формулы для A и B приведены в Международных таблицах для рентгеновской кристаллографии , том 1, 1969. , (Бирмингем, Kynoch Press). Расчеты обычно производятся на компьютере.
Наконец, следует упомянуть, что всякий раз, когда набор атомов, для которого выполняется расчет структурного фактора, имеет центр симметрии, результирующий структурный фактор всегда полностью реален, и, следовательно, соответствующие фазовые углы всегда равны 0 или 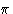 .В том, что это так, легко убедиться, разделив структуру на центросимметрично связанные пары. Для каждого атома при x , y , z будет один атом при — x , — y , — z и, следовательно, мнимые части, B ‘структурного фактора. , поскольку они содержат синусоидальный член, будут иметь противоположный знак и сокращаться.
.В том, что это так, легко убедиться, разделив структуру на центросимметрично связанные пары. Для каждого атома при x , y , z будет один атом при — x , — y , — z и, следовательно, мнимые части, B ‘структурного фактора. , поскольку они содержат синусоидальный член, будут иметь противоположный знак и сокращаться.
.
Расчет среднего и стандартного отклонения с помощью Excel
В поисках среднего
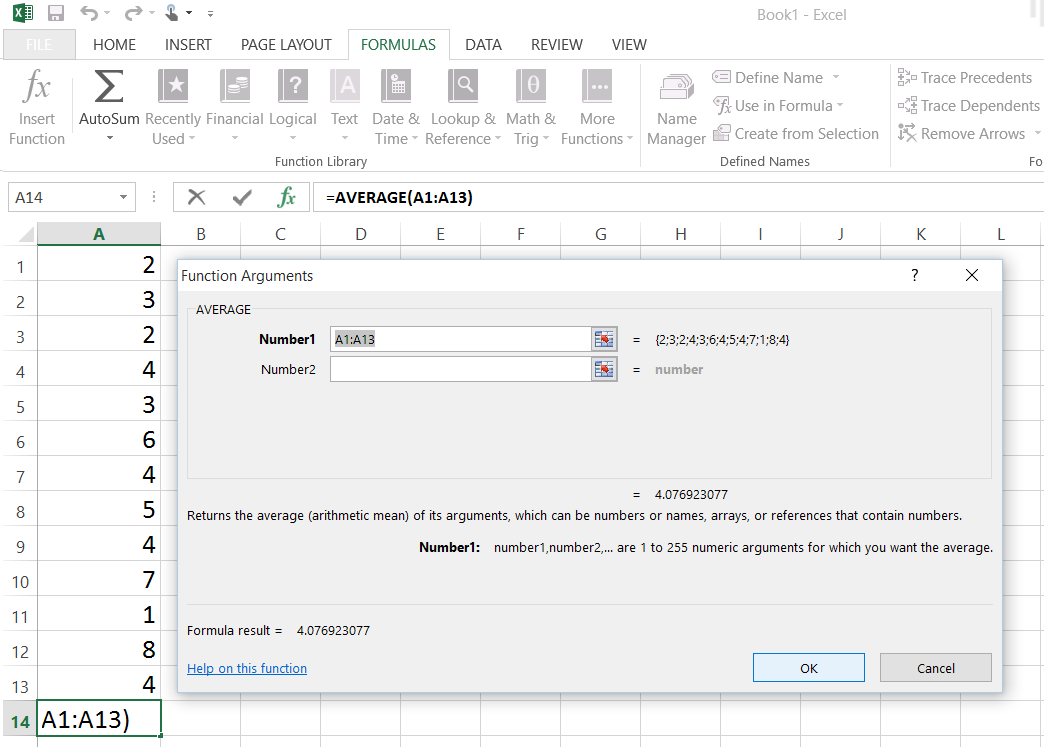
Введите результаты в один из столбцов электронной таблицы Excel (см. Пример ниже). После того, как данные были введены, поместите курсор в то место, где должно появиться среднее (среднее), и щелкните кнопкой мыши. Выберите Insert Function ( f x ) на вкладке FORMULAS . Появится диалоговое окно. Выберите СРЕДНИЙ из категории Статистический и щелкните ОК .(Примечание: если вам нужна медиана, выберите MEDIAN . Если вам нужен режим, выберите MODE.SNGL . Excel предоставляет только один режим. Если в наборе данных было более одного режима, Excel отобразит только один из них .)

Введите диапазон ячеек для вашего списка чисел в поле Число 1 . Например, если ваши данные находятся в столбце A от 1 до 13, вы должны ввести A1: A13. Вместо того, чтобы вводить диапазон, вы также можете переместить курсор в начало набора партитур, который вы хотите использовать, и щелкнуть и перетащить курсор по ним.После того, как вы ввели диапазон для своего списка, нажмите OK внизу диалогового окна. Среднее (среднее) значение для списка появится в выбранной вами ячейке.
Определение стандартного отклонения
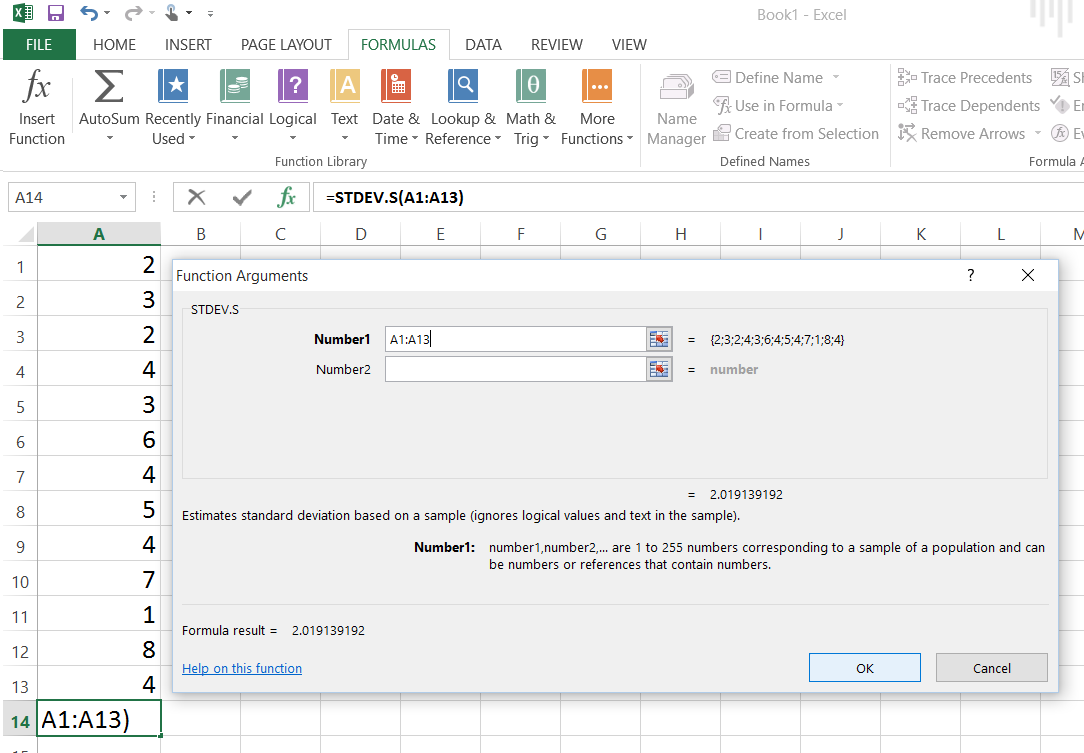
Поместите курсор в то место, где должно появиться стандартное отклонение, и щелкните кнопкой мыши. Выберите Вставить функцию (f x ) на вкладке FORMULAS . Появится диалоговое окно. Выберите STDEV.S (для образца) из категории Statistical . (Примечание: если ваши данные относятся к населению, щелкните STDEV.P) . После того, как вы сделали свой выбор, нажмите OK внизу диалогового окна.
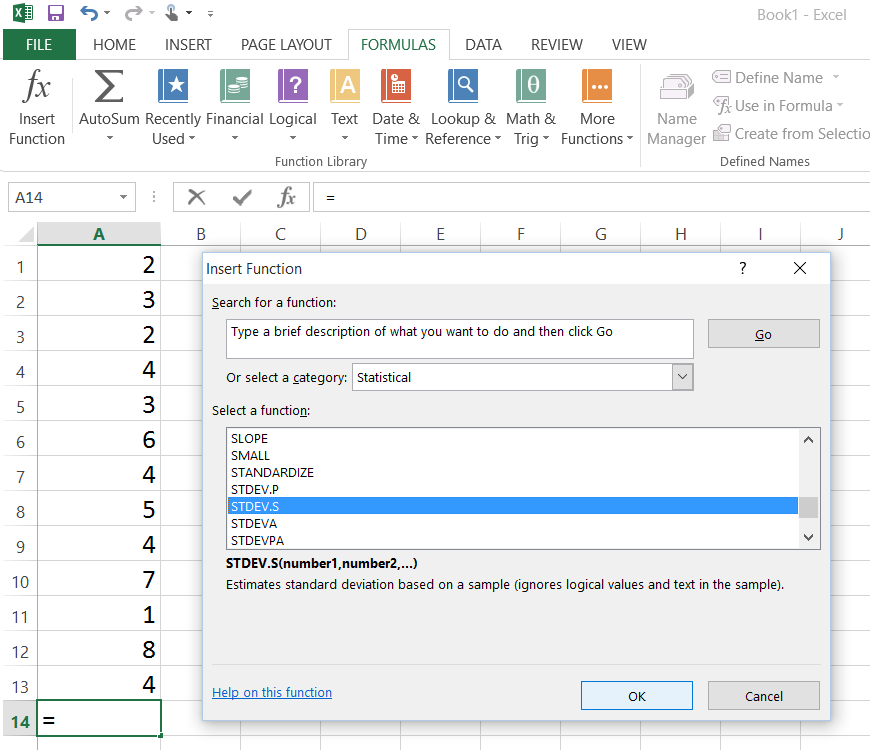
Введите диапазон ячеек для вашего списка чисел в поле Число 1 . Например, если ваши данные находятся в столбце A от 1 до 13, вы должны ввести A1: A13. Вместо того, чтобы вводить диапазон, вы также можете переместить курсор в начало набора партитур, который вы хотите использовать, и щелкнуть и перетащить курсор по ним.После того, как вы ввели диапазон для своего списка, нажмите OK внизу диалогового окна. Стандартное отклонение для списка появится в выбранной вами ячейке.
Дель Зигл, доктор философии
Neag School of Education — Университет Коннектикута
del.siegle@uconn.edu
www.delsiegle.com
.

 Как рассчитать базовые характеристики армирующего каркаса плитного фундамента?
Как рассчитать базовые характеристики армирующего каркаса плитного фундамента? Метры в тонны? – нет ничего проще!
Метры в тонны? – нет ничего проще! Как самостоятельно залить плитный фундамент?
Как самостоятельно залить плитный фундамент? Площадь сечения основания такова: 70*40=2800 см2.
Площадь сечения основания такова: 70*40=2800 см2. Определите тип грунта посредством ГОСТа «Грунты. Классификация».
Определите тип грунта посредством ГОСТа «Грунты. Классификация». Как определить оптимальную толщину монолитной фундаментной плиты?
Как определить оптимальную толщину монолитной фундаментной плиты?