Расчет стены в грунте: Справочник проектировщика. Основания, фундаменты и подземные сооружения
Справочник проектировщика. Основания, фундаменты и подземные сооружения
Оглавление 4
Предисловие 8
Основные условные обозначения 10
Глава 1. Свойства грунтов (О. И. Игнатова) 10
1.1. Происхождение и состав грунтов 10
1.2. Физические свойства грунтов 11
1.2.1. Характеристики плотности грунтов и плотности их сложения 11
1.2.2. Влажность грунтов и характеристики пластичности пылевато-глинистых грунтов 11
1.3. Классификация грунтов 11
1.4. Деформируемость грунтов при сжатии 14
1.4.1. Определение модуля деформации в полевых условиях 15
1.4.2. Определение модуля деформации в лабораторных условиях 16
1.5. Прочность грунтов 16
1.5.1. Определение прочностных характеристик в лабораторных условиях 17
1.5.2. Определение прочностных характеристик в полевых условиях 18
1.6. Фильтрационные свойства грунтов 19
1.7. Нормативные и расчётные значения характеристик грунтов 20
Список литературы 23
Глава 2.
Инженерно-геологические изыскания (Л. Г. Мариупольский) 24
2.1. Общие сведения 24
2.2. Требования к техническому заданию и программе изысканий 24
2.3. Этапы, состав и объем изысканий 26
2.4. Основные принципы назначения состава и объёма исследований грунтов 28
2.5. Представление результатов инженерно-геологических изысканий 31
Список литературы 31
Глава 3. Общие принципы выбора типа оснований и фундаментов (P. X. Валеев, Ю. Г. Трофименков, Р. Е. Ханин) 32
3.1. Основные положения 32
3.2. Типы оснований и фундаментов и область их применения 32
3.3. Технико-экономические показатели и их назначение 32
3.4. Факторы, влияющие на выбор технико-экономических показателей 33
3.5. Принципы сопоставимости конструктивных решений фундаментов различных типов зданий и сооружений 34
3.6. Рекомендации для выбора оснований и фундаментов 34
3.7. Методика технико-экономических сравнений фундаментов различных типов 35
3.
8. Экспресс-методы технико-экономической оценки фундаментов различных типов 36
3.9. Удельные показатели стоимости и трудоёмкости основных видов работ при устройстве фундаментов 38
Список литературы 39
Глава 4. Конструкции фундаментов мелкого заложения (Е. А. Сорочан) 40
4.1. Основные положения 40
4.2. Материалы фундаментов 40
4.3. Конструкции фундаментов 45
4.3.1. Столбчатые фундаменты под стены 45
4.3.2. Ленточные и прерывистые фундаменты под стены 45
4.3.3. Отдельные фундаменты под колонны 50
4.3.4. Ленточные и плитные фундаменты под колонны 58
Список литературы 58
Глава 5. Расчёт оснований фундаментов мелкого заложения (пп. 5.1 — 5.5 (кроме 5.5.2 и 5.5.3А), п. 5.7 — А. В. Вронский; пп. 5.5.2 и 5.5.3А — Е. А. Сорочан; п. 5.6 – А. С. Снарский) 59
5.1. Основные положения 59
5.2. Распределение напряжений в основаниях 61
5.
2.1. Однородное основание 61
5.2.2. Неоднородное основание 66
5.2.3. Напряжения от собственного веса грунта 68
5.3. Нагрузки и воздействия, учитываемые в расчётах оснований 68
5.4. Глубина заложения фундаментов 69
5.5. Расчёт оснований по деформациям 74
5.5.1. Общие положения 74
5.5.2. Расчётное сопротивление грунтов основания 76
5.5.3. Определение основных размеров фундаментов 80
5.5.4. Расчёт деформаций основания 84
5.5.5. Предельные деформации основания 93
5.6. Расчёт оснований по несущей способности 96
5.6.1. Общие положения 96
5.6.2. Несущая способность оснований, сложенных грунтами, находящимися в стабилизированном состоянии 97
5.6.3. Расчёт устойчивости фундамента по схеме плоского сдвига 105
5.6.4. Графоаналитический метод расчёта несущей способности основания (метод круглоцилиндрических поверхностей скольжения) 106
5.
6.5. Несущая способность оснований, сложенных медленно уплотняющимися водонасыщенными пылевато-глинистыми и биогенными грунтами, а также илами 108
5.7. Мероприятия по уменьшению деформаций оснований и влияния их на сооружение 109
Список литературы 110
Глава 6. Проектирование конструкций фундаментов (п. 6.1 — Л. В. Шапиро, Е. А. Сорочан, п. 6.2 — 6.4 — Е. А. Сорочан; п. 6.5 — М. И. Горбунов-Посадов) 111
6.1. Расчёт железобетонных фундаментов на естественном основании под колонны зданий и сооружений 111
6.1.1. Общие положения 111
6.1.2. Расчёт фундаментов на продавливание 111
6.1.3. Определение площади сечений арматуры плитной части 114
6.1.4. Расчёт плитной части на «обратный» момент 114
6.1.5. Расчёт прочности поперечных сечений подколонника 115
6.2. Расчёт ленточных фундаментов и стен подвалов 118
6.2.1. Общие положения 118
6.2.2. Расчёт ленточных фундаментов 119
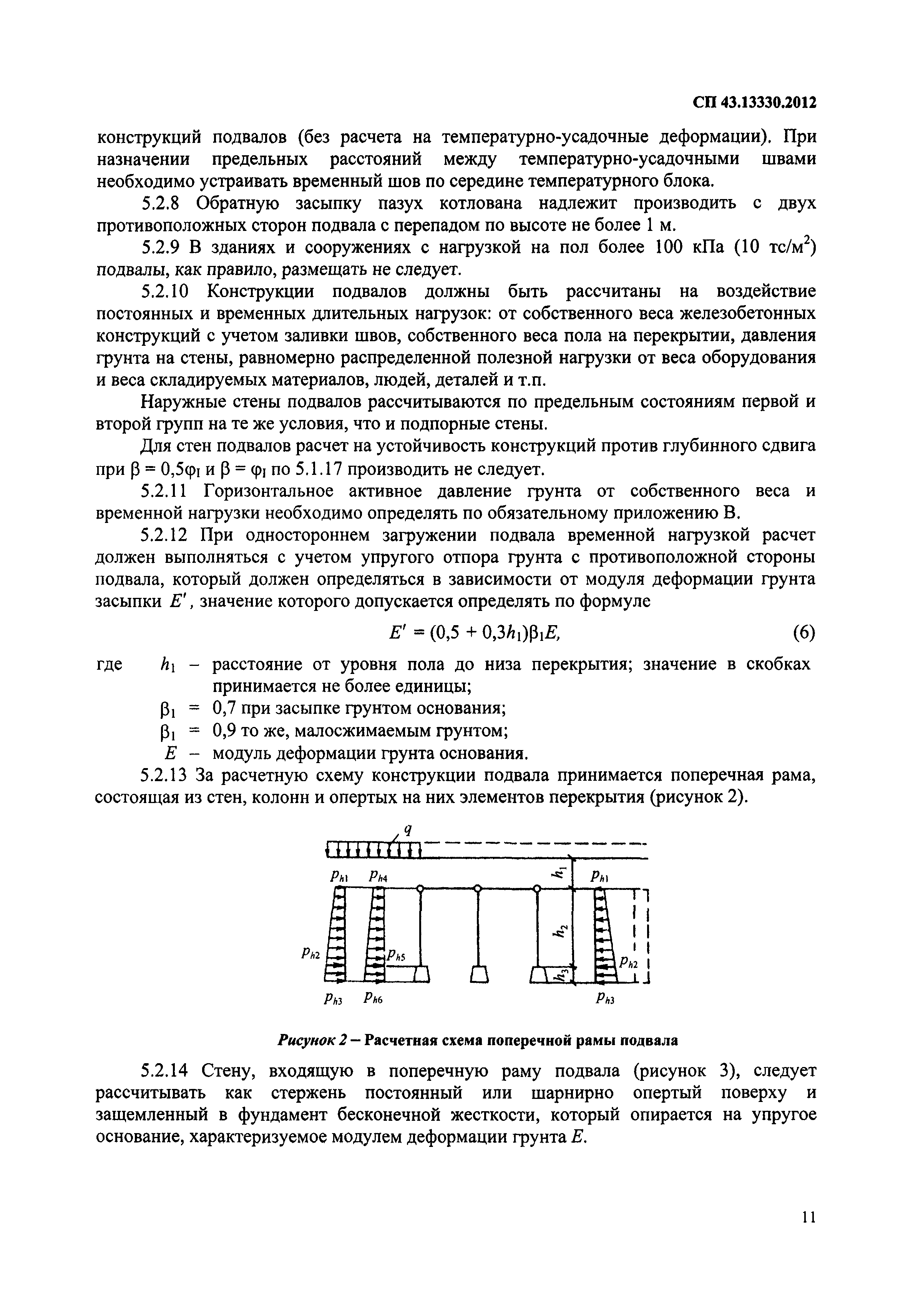
6.
2.3. Расчёт стен подвалов 121
6.3. Расчёт буробетонных фундаментов 123
6.3.1. Общие положения 123
6.3.2. Метод расчёта 124
6.4. Расчёт фундаментов с анкерами в нескальных грунтах 127
6.4.1. Общие положения 127
6.4.2. Метод расчёта 128
6.5. Расчёт плитных и ленточных фундаментов под колонны 132
6.5.1. Общие положения 132
6.5.2. Предварительное назначение размеров сечений 132
6.5.3. Расчёт фундаментных балок и плит как конструкций на упругом основании 133
6.5.4. Связь между расчётными значениями модуля деформации и коэффициента постели 133
6.5.5. Определение расчётных значений модуля деформации 134
6.5.6. Методы расчёта конструкций 134
6.5.7. Расчёт конструкций на упругом основании по таблицам 135
Список литературы 147
Глава 7. Расчёт и проектирование подпорных стен (А. С. Снарский) 148
7.1. Типы подпорных стен 148
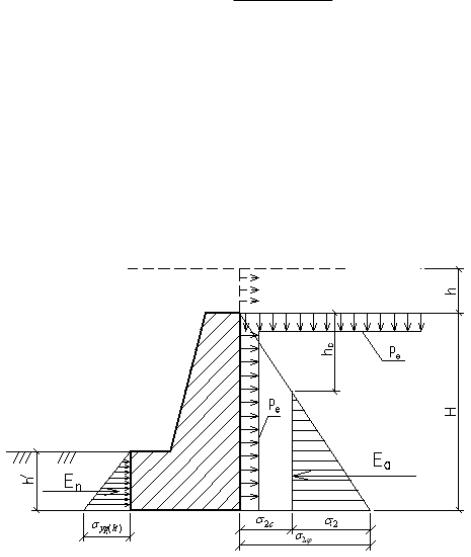
7.
2. Определение активного и пассивного давления грунта на стены 148
7.2.1. Общие положения 149
7.2.2. Характеристики грунта, используемые при определении давления грунта 149
7.2.3. Активное давление грунта 149
7.2.4. Пассивное давление грунта 151
7.3. Расчёт массивных и уголковых подпорных стен 151
7.3.1. Общие положения 151
7.3.2. Расчёт устойчивости оснований стен против сдвига по подошве и глубокого сдвига по ломаным поверхностям скольжения 151
7.3.3. Расчёт оснований подпорных стен по деформациям 152
7.4. Расчёт гибких незаанкерных подпорных стен 154
7.4.1. Общие положения 154
7.4.2. Параметры грунта и стен, необходимые для расчёта 154
7.4.3. Давление грунта 155
Список литературы 156
Глава 8. Проектирование свайных фундаментов (Б. В. Бахолдин, Г. М. Лешин, Р. Е. Ханин) 157
8.1. Номенклатура и область применения свай различных видов 157
8.
1.1. Государственные стандарты на сваи 157
8.1.2. Составные сваи квадратного сечения 158
8.1.3. Сваи-колонны 159
8.1.4. Бурозабивные сван 160
8.1.5. Набивные сваи в уплотнённом основании 164
8.1.6. Пирамидальные сваи 165
8.1.7. Прочие виды свай 165
8.2. Расчёт свай и свайных фундаментов 166
8.2.1. Методы определения несущей способности свай и область их применения 166
8.2.2. Расчёт свай на горизонтальные нагрузки и изгибающие моменты 169
8.2.3. Расчёт свай по прочности и раскрытию трещин 178
8.2.4. Расчёт осадок свайных фундаментов 179
8.2.5. Расчёт кренов свайных фундаментов 183
8.2.6. Расчёт железобетонных ростверков 184
8.3. Проектирование свай и свайных фундаментов 186
8.3.1. Исходные данные для проектирования 186
8.3.2. Выбор типа свайных фундаментов и нагрузок на них 187
3.3.3. Выбор несущего слоя грунтов и определение размеров свай 188
8.
3.4. Проектирование свайного поля и ростверков 188
8.3.5. Состав проекта свайных фундаментов 199
8.3.6. Особенности проектирования свайных фундаментов в лёссовых просадочных грунтах 200
8.4. Конструктивные решения свайных фундаментов 200
8.4.1. Свайные фундаменты жилых домов 200
8.4.2. Фундаменты из забивных свай для каркасных зданий 201
8.4.3. Фундаменты из буронабивных свай для каркасных зданий 201
8.4.4. Свайные фундаменты каркасных зданий со сборными ростверками 202
8.4.5. Безростверковые свайные фундаменты каркасных зданий 202
8.4.6. Фундаменты из свайных полей 203
8.4.7. Свайные фундаменты вблизи заглубленных сооружений и фундаментов под оборудование 205
8.4.8. Бескотлованные свайные фундаменты 206
8.5. Выполнение свайных работ 206
8.5.1. Погружение свай заводского изготовления 207
8.5.2. Подбор молота для погружения свай 208
8.
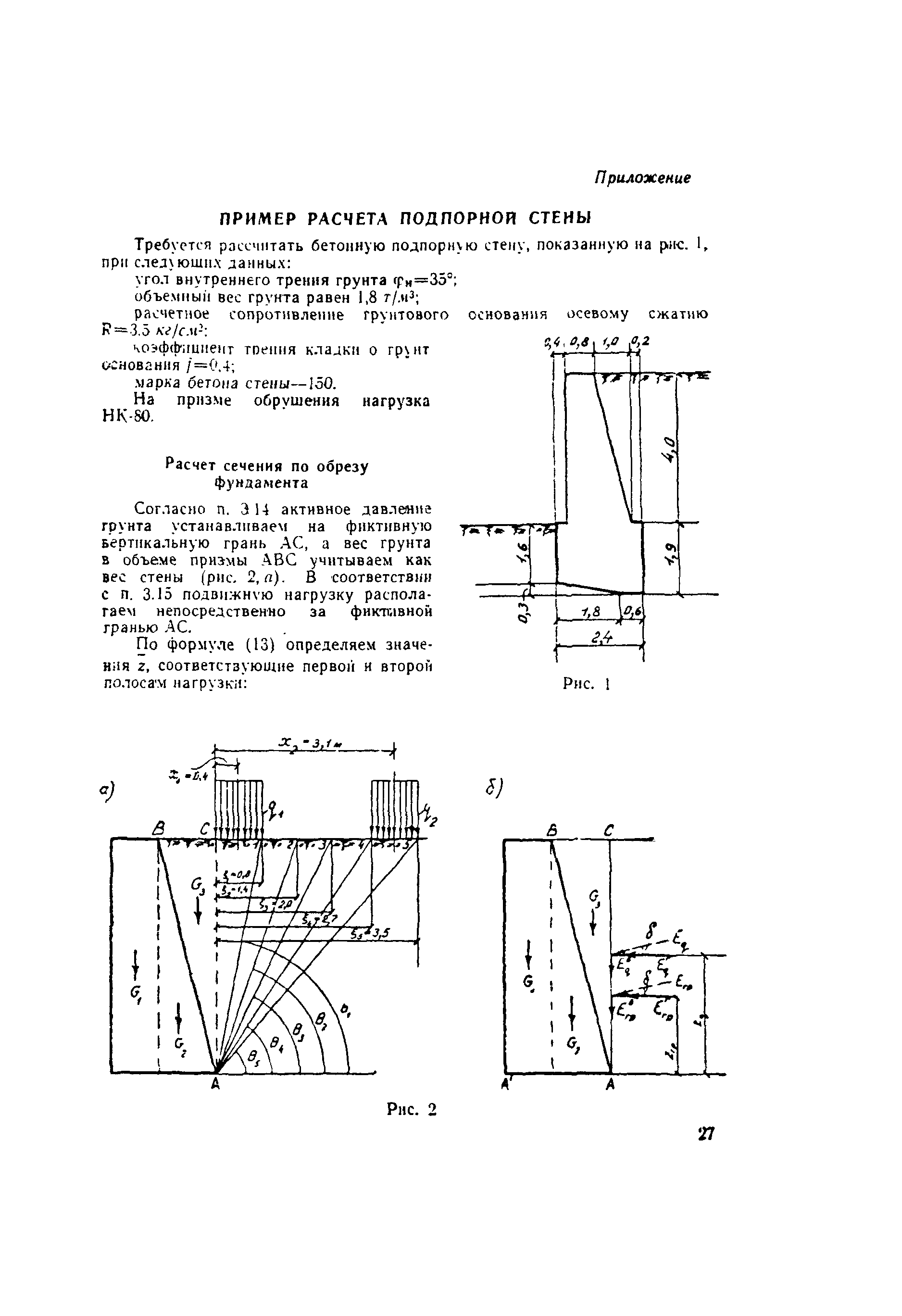5.3. Изготовление буронабивных свай 211
8.5.4. Контроль и приёмка свайных фундаментов 215
Список литературы 217
Глава 9. Расчёт и проектирование фундаментов машин и оборудования с динамическим и нагрузками (В. Л. Ильичев, В. А. Михальчук) 217
9.1. Основные положения расчёта 217
9.1.1. Расчёт по первой группе предельных состояний 218
9.1.2. Расчёт по второй группе предельных состояний 219
9.2. Определение упругих и демпфирующих характеристик основания для расчёта фундаментов 220
9.2.1. Коэффициенты жесткости и демпфирования для фундаментов на естественном основании 220
9.2.2. Коэффициенты жесткости и демпфирования для свайных фундаментов. Определение приведённой массы 221
9.3. Принципы проектирования 222
9.3.1. Исходные данные для проектирования фундаментов машин и оборудования 222
9.3.2. Основные требования по проектированию фундаментов машин с динамическими нагрузками 223
9.
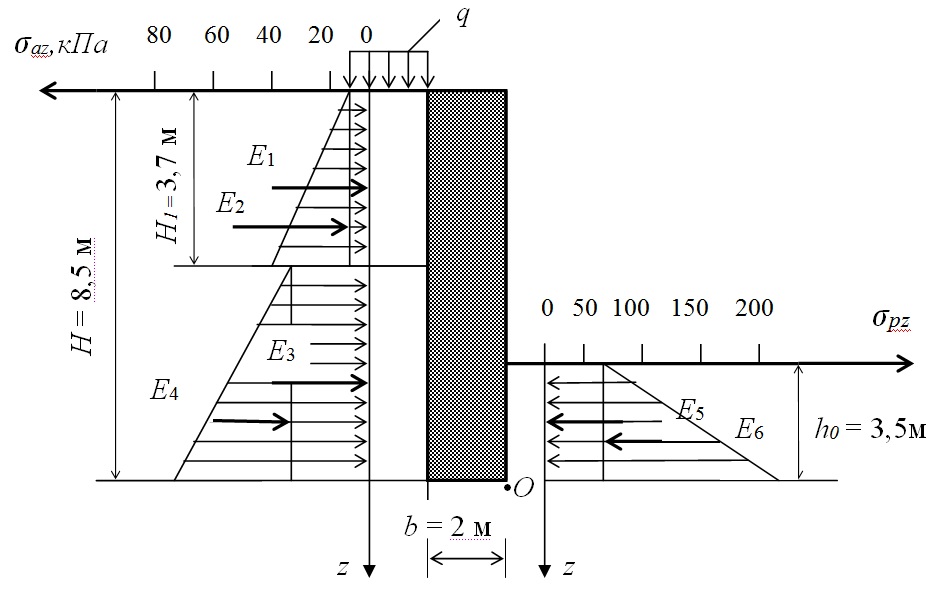3.3. Конструктивные решения фундаментов машин с динамическими нагрузками 224
9.4. Распространение колебаний от фундаментов-источников и мероприятия по их уменьшению 224
9.5. Примеры расчёта колебании фундаментов машин с динамическими нагрузками 226
Список литературы 230
Глава 10. Проектирование оснований сооружений, возводимых на структурно-неустойчивых грунтах (п. 10.1 — В. В. Крутов; п. 10.2 — Е. А. Сорочан) 231
10.1. Проектирование оснований на просадочных грунтах 231
10.1.1. Общие положения 231
10.1.2. Расчёт просадочных деформаций 232
10.1.3. Расчёт оснований 235
10.1.4. Проектирование уплотнённых оснований 237
10.1.5. Водозащитные мероприятия 243
10.1.6. Мероприятия по обеспечению нормальной эксплуатации деформировавшихся зданий 245
10.2. Проектирование оснований и фундаментов на набухающих грунтах 246
10.2.1. Общие положения 246
10.
2.2. Исходные данные для проектирования 246
10.2.3. Проектирование оснований и фундаментов 247
Список литературу 251
Глава 11. Проектирование оснований на сильносжимаемых и насыпных грунтах (л. 11.1.1 — 11.1.6 — П. А. Коновалов; п. 11.1.7 — В. М. Казанцев, п. 11.2 — В. Я. Крутов) 252
11.1. Проектирование оснований на сильносжимаемых грунтах 252
11.1.1. Общие положения 252
11.1.2. Проектирование предпостроечного уплотнения оснований, сложенных водонасыщенными сильносжимаемыми грунтами 252
11.1.3. Методы расчёта осадок и сроков консолидации оснований 255
11.1.4. Особенности расчёта оснований 257
11.1.5. Методика определения коэффициента консолидации 257
11.1.6. Конструктивные мероприятия 258
11.1.7. Особенности расчёта и конструирования оснований и фундаментов стальных вертикальных резервуаров 259
11.2. Проектирование оснований на насыпных грунтах 261
11.
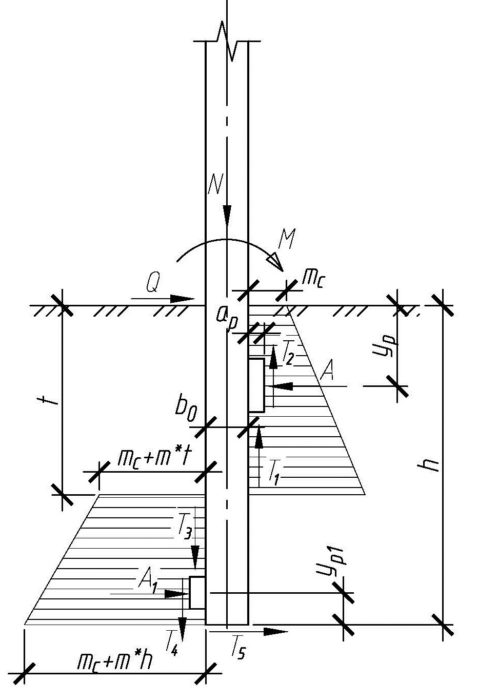2.1. Общие положения 261
11.2.2. Расчёт оснований на насыпных грунтах 262
11.2.3. Проектирование оснований на насыпных грунтах 264
Список литературы 267
Глава 12. Проектирование фундаментов в особых условиях (п. 12.1 — А. И. Юшин; п. 12.2 – В. А. Ильичев; п. 12.3 – Е. А. Сорочан) 268
12.1. Особенности проектирования оснований и фундаментов на подрабатываемых территориях 268
12.1.1. Деформации земной поверхности, вызываемые горными выработками, и их воздействие на конструкции зданий 268
12.1.2. Принципы проектирования оснований и фундаментов на подрабатываемых территориях 268
12.1.3. Расчёт фундаментов на естественном основании на воздействие горизонтальных деформаций 270
12.1.4. Проектирование и расчёт свайных фундаментов на подрабатываемых территориях 274
12.2. Сейсмостойкость оснований и фундаментов 278
12.2.1. Общие положения 278
12.2.2. Оценка интенсивности сейсмических колебаний в зависимости от грунтовых условий 278
12.
2.3. Влияние упругой податливости основания на периоды свободных колебаний зданий и сооружений 279
12.2.4. Принципы расчёта и требования по конструированию сейсмостойких оснований и фундаментов 282
12.2.5. Сейсмостойкость фундаментов на естественных основаниях 283
12.2.6. Сейсмостойкость свайных фундаментов 286
12.3. Проектирование фундаментов на закарстованных территориях 294
Список литературы 298
Глава 13. Проектирование искусственных оснований (п. 13.1 — В. И. Крутов, Б. С. Смолин; п. 13.2 – А. Н. Токин; п. 13.3 — Б. С. Смолин) 299
13.1. Поверхностное и глубинное уплотнение грунтов 299
13.1.1. Общие положения 299
13.1.2. Исходные данные для проектирования 301
13.1.3. Уплотнение грунтов укаткой 302
13.1.4. Уплотнение трамбующими машинами 304
13.1.5. Уплотнение грунтов тяжёлыми трамбовками 304
13.1.6. Вытрамбовывание котлованов 306
13.
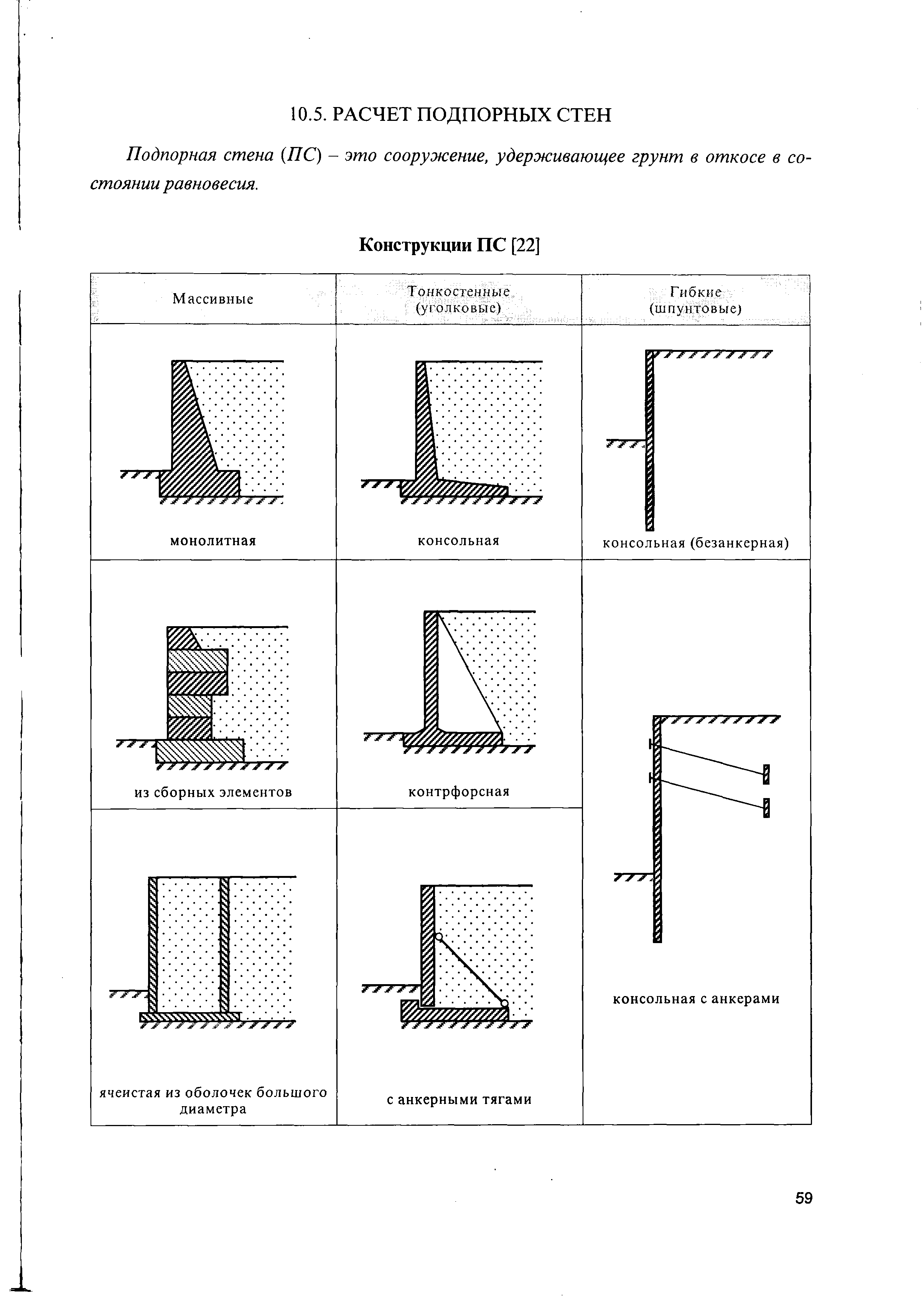1.7. Глубинное уплотнение пробивкой скважин 308
13.1.8. Уплотнение подводными и глубинными взрывами 310
13.2. Инъекционное закрепление грунтов способами силикатизации и смолизации 311
13.2.1. Общие положения 311
13.2.2. Расчёт основных параметров 315
13.2.3. Оборудование для производства работ 316
13.2.4. Технологическая схема закрепления 318
13.2.5. Проектирование оснований и фундаментов из химически закреплённых инъекций грунтов 320
13.2.6. Проектирование закреплённых силикатизацией массивов в просадочных лессовых грунтах 321
13.3. Глубинное вибрационное уплотнение рыхлых песчаных грунтов 325
13.3.1. Общие положения 325
13.3.2. Исходные данные для проектирования и расчёта 326
13.3.3. Методы расчёта 326
13.3.4. Оборудование для производства работ 327
13.3.5. Данные для проектирования производства работ 328
Список литературы 329
Глава 14.
Устойчивость откосов (М. Л. Моргулис) 330
14.1. Конструктивные решения и мероприятия 330
14.2. Исходные данные для проектирования 331
14.3. Методы и примеры расчётов 333
14.3.1. Общие сведения 333
14.3.2. Построение предельных откосов 333
14.3.3. Определение угла плоских откосов при горизонтальной поверхности грунта 334
14.3.4. Определение ширины призмы обрушения откоса 336
14.3.5. Основные принципы определения требуемого контура откоса в сложных условиях 338
14.3.6. Расчёт устойчивости отсека грунтового массива против сдвига по выбранной поверхности 340
14.3.7. Определение давления грунта на удерживающие сооружения на откосе 348
Список литературы 351
Глава 15. Проектирование опускных колодцев и оболочек (В. К. Демидов) 352
15.1. Общие сведения 352
15.2. Конструктивные решения 353
15.3. Исходные данные для разработки проектной документации 357
15.
4. Методы расчётов 359
15.5. Проект производства работ 367
15.6. Основные машины и механизмы, применяемые при сооружении и опускании колодцев 374
15.7. Примеры расчёта 374
Список литературы 377
Глава 16. Проектирование подземных сооружений, устраиваемых способом «стена в грунте» (И. К. Коньков, М. Я. Смородинов, Б. С. Федоров) 378
16.1. Общие положения 378
16.2. Исходные данные для разработки проектной документации 378
16.3. Конструктивные решения 379
16.4. Оборудование, применяемое при строительстве способом «стена в грунте» 383
16.4.1. Оборудование для приготовления и очистки глинистой суспензии 383
16.4.2. Оборудование для разработки траншей 384
16.5. Проект производства работ 386
16.5.1. Общие положения 386
16.5.2. Приготовление глинистой суспензии (раствора) 386
16.5.3. Разработка траншей 387
16.5.4. Заполнение траншей монолитным или сборным железобетоном 388
16.
5.5. Контроль качества и приёмка работ 390
16.6. Расчёт конструкций 391
Список литературы 393
Глава 17. Анкеры в грунте (Ю. В. Лабзов, М. И. Смородинов) 394
17.1. Общие положения 394
17.2. Конструктивные решения 394
17.3. Методы расчёта 398
17.4. Технология работ 402
Список литературы 406
Глава 18. Укрепление оснований и усиление фундаментов существующих зданий и сооружений (Е. Ф. Лаш) 407
18.1. Общие положения 407
18.2. Исходные данные 407
18.3. Укрепление оснований существующих зданий 408
18.3.1. Цементация 408
18.3.2. Дренаж и противофильтрационные завесы 409
18.3.3. Повышение несущей способности (устойчивости) оснований 411
18.3.4. Защита оснований от влияния строящихся рядом зданий и сооружений 412
18.4. Усиление (укрепление) фундаментов 412
18.4.1. Защита фундаментов от выветривания 412
18.
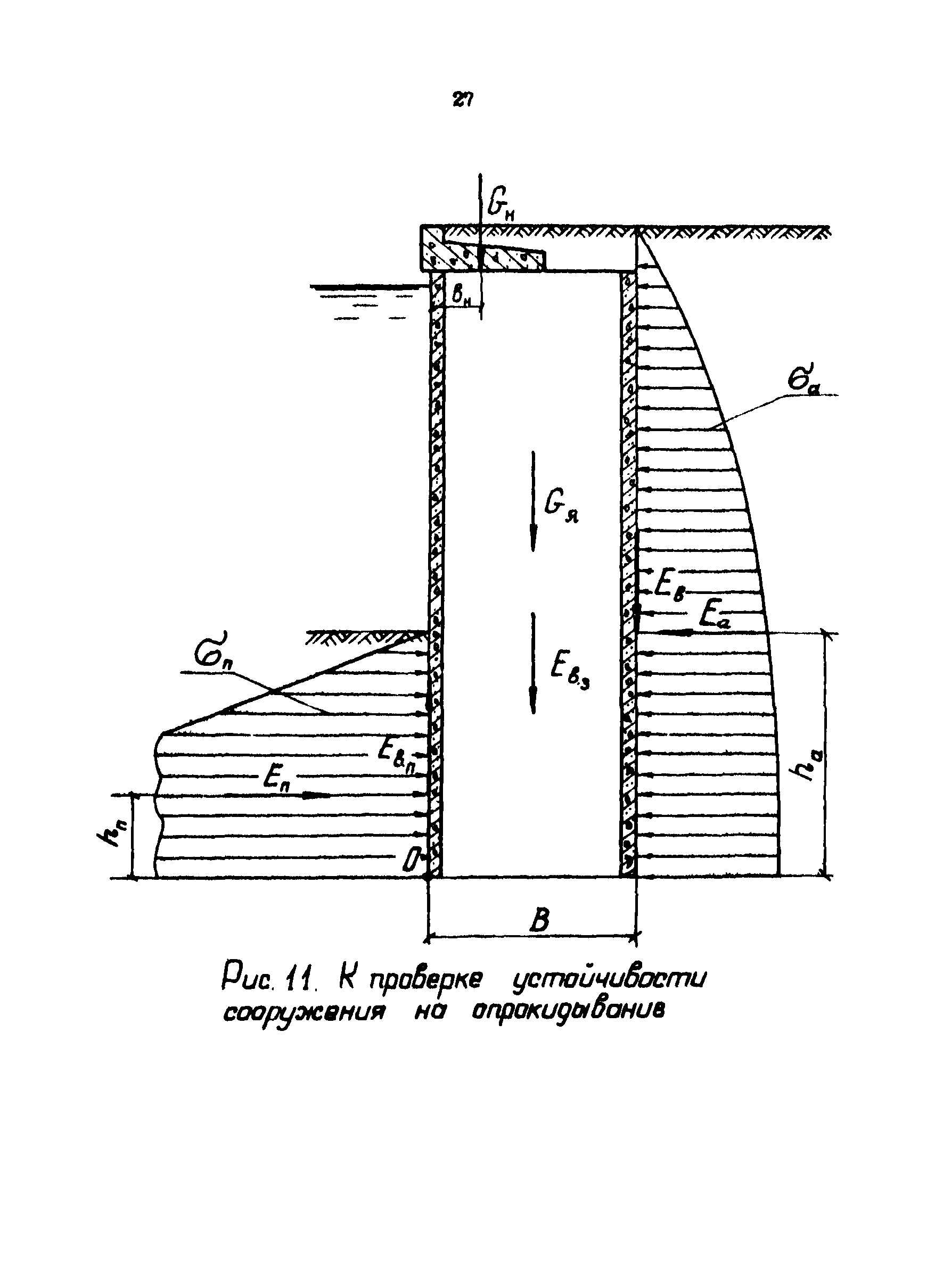4.2. Повышение прочности и уширение фундамента 413
18.4.3. Подведение свай 414
Список литературы 416
Глава 19. Водопонижение (М. Л. Моргулис, Б. Н. Фомин) 417
19.1. Общие положения 417
19.2. Конструктивные решения 417
19.2.1. Водоотлив 417
19.2.2. Дренаж 418
19.2.3. Открытые водопонизительные скважины 423
19.2.4. Вакуумные скважины 425
19.2.5. Водоприёмная часть водопонизительных скважин 426
19.2.6. Песчано-гравийная обсыпка трубчатых дренажей и водопонизительных скважин 426
19.2.7. Иглофильтры 430
19.2.8. Наблюдательные скважины 431
19.2.9. Водопонизительные системы 431
19.2.10. Отвод воды от водопонизительных систем 434
19.3. Исходные данные для проектирования 434
19.4. Методы расчётов 435
19.4.1. Основные положения по расчётам водопонизительных систем 435
19.4.2. Определение притока подземных вод 436
19.
4.3. Расчёт скважинных водопонизительных систем 445
19.4.4. Расчёт иглофильтровых водопонизительных систем 450
19.4.5. Расчёт дренажей 453
19.5. Оборудование и производство работ 455
19.5.1. Водоотлив 455
19.5.2. Дренаж 455
19.5.3. Водопонизительные скважины 456
19.5.4. Устройство иглофильтровых установок 458
Список литературы 458
Глава 20. Проектирование котлованов (Л. И. Иванов) 459
20.1. Общие сведения 459
20.2. Расчёт креплений котлованов 460
20.2.1. Расчёт тонких (гибких) свободно стоящих стенок 460
20.2.2. Расчёт тонких (гибких) заанкеренных стенок 464
20.2.3. Расчёт анкерных опор 468
20.2.4. Расчёт основных конструктивных элементов тонких стенок 470
Список литературы 471
Предметный указатель 472
ГОСТ Р 57361-2016/EN ISO 13793:2001 Фундаменты зданий. Теплотехнический расчет
ГОСТ Р 57361-2016/EN ISO 13793:2001
ОКС 93.
020
Дата введения 2017-07-01
Предисловие
1 ПОДГОТОВЛЕН Акционерным обществом «Научно-исследовательский центр «Строительство», Научно-исследовательский, проектно-изыскательский и конструкторско-технологический институт оснований и подземных сооружений имени Н.М.Герсеванова (АО «НИЦ «Строительство» НИИОСП им.Н.М.Герсеванова) на основе официального перевода на русский язык англоязычной версии указанного в пункте 4 международного стандарта, который выполнен Федеральным государственным унитарным предприятием «Российский научно-технический центр информации по стандартизации, метрологии и оценке соответствия» (ФГУП «СТАНДАРТИНФОРМ»)
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 465 «Строительство»
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 13 декабря 2016 г. N 2031-ст
4 Настоящий стандарт идентичен европейскому стандарту EN ISO 13793:2001* «Тепловая характеристика зданий.
Тепловой расчет фундаментов для предупреждения морозного пучения» (EN ISO 13793:2001 «Thermal performance of buildings — Thermal design of foundations to avoid frost heave», IDT).
________________
* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей. — Примечание изготовителя базы данных.
Наименование настоящего стандарта изменено относительно наименования указанного европейского стандарта для приведения в соответствие с ГОСТ Р 1.5-2012 (пункт 3.5).
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты, сведения о которых приведены в дополнительном приложении ДА
5 ВВЕДЕН ВПЕРВЫЕ
Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ «О стандартизации в Российской Федерации». Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе «Национальные стандарты», а официальный текст изменений и поправок — в ежемесячном информационном указателе «Национальные стандарты».
В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования — на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)
1 Область применения
В настоящем стандарте представлены упрощенные методики теплофизического расчета фундаментов зданий для исключения возможности возникновения морозного пучения грунта.
Стандарт применяется к фундаментам, устраиваемым на пучинистых грунтах, для зданий с полами из плит на грунтовом основании и подвесными полами.
Стандарт распространяется как на отапливаемые, так и на неотапливаемые здания, но в него не включены другие сооружения, требующие защиты от промерзания (например, дороги, водопровод в грунте и др.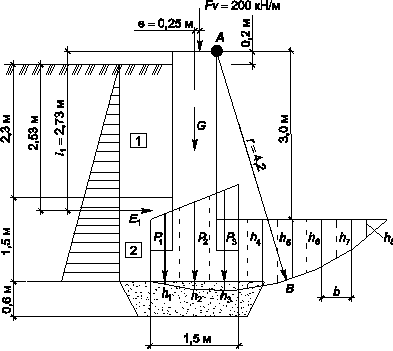
).
Стандарт не применяется к холодильным складам и ледовым каткам.
Стандарт применяется в климатических районах со средней годовой температурой воздуха выше 0°С, но не применяется в зонах распространения многолетнемерзлых грунтов, где средняя годовая температура воздуха ниже 0°С.
2 Нормативные ссылки
Настоящий стандарт включает в себя нормативные и справочные ссылки*, положения из других публикаций. Эти нормативные ссылки приведены в соответствующих местах в тексте, а публикации перечислены ниже. Для нормативных ссылок последующие изменения или пересмотры любой из этих публикаций применяются к настоящему стандарту, только когда включены в него в качестве изменения или пересмотра. Для недатированных ссылок необходимо использовать самые последние издания публикации (включая изменения).
_______________
* Таблицу соответствия национальных стандартов международным см. по ссылке. — Примечание изготовителя базы данных.
ISO 6946, Building components and building elements — Thermal resistance and thermal transmittance — Calculation method (Компоненты и элементы строительные.
Теплостойкость и коэффициент теплопередачи. Метод расчета)
ISO 7345, Thermal insulation — Physical quantities and definitions (Теплоизоляция. Физические величины и определения)
ISO 10211-1, Thermal bridges in building construction — Heat flows and surface temperatures — Part 1: General calculation methods (Тепловые мостики в зданиях. Тепловые потоки и температуры поверхности. Часть 1. Общие методы расчета)
________________
Отменен. Действует ISO 10211.
ISO 10456, Building materials and products — Tabulated design values and procedures for determining declared and design thermal values (Теплоизоляция. Строительные материалы и изделия. Определение заявленных и расчетных значений тепловых свойств
3 Термины, обозначения и единицы измерения
3.1 Термины и определения
В настоящем стандарте применены термины по ISO 7345, а также следующие термины с соответствующими определениями:
3.
1.1 пол из плит на грунтовом основании (slab on ground floor): Конструкция пола, расположенного непосредственно на грунте по всей площади сооружения.
3.1.2 подвесной пол (suspended floor): Конструкция пола, в которой пол удерживается над грунтом, образуя воздушное пространство между полом и грунтом.
Примечание — Эта пустота, называемая подпольем или погребом, может проветриваться или нет, но не является частью жилого пространства.
3.1.3 вертикальная теплоизоляция (краевая, по периметру) (vertical edge insulation): Теплоизоляция, расположенная вертикально к фундаменту внутри и/или снаружи, либо внутри самого фундамента.
3.1.4 теплоизоляция грунта (ground insulation): Теплоизоляция, расположенная горизонтально (или почти горизонтально) ниже пола, снаружи здания.
Примечание — См. рисунок 1.
3.1.5 индекс промерзания грунта (индекс мороза) (freezing index): Увеличенная в 24 раза сумма разности между 0°С и средней суточной температурой наружного воздуха, накопленная за сутки в течение зимнего периода (включая как положительные, так и отрицательные разности).
3.1.6 зимний период (freezing season): Период, в течение которого среднесуточная температура наружного воздуха остается ниже 0°С, вместе с любыми периодами промерзания/таяния в любом конце этого периода, если они кончаются общим замерзанием.
3.1.7 глубина промерзания (frost depth): Глубина проникновения отрицательных температур в грунт с образованием льда.
3.1.8 глубина заложения фундамента (foundation depth): Глубина от поверхности грунта до подошвы фундамента.
Примечание — Если фундаменты опираются на слой хорошо дренированного материала, который не подвержен промерзанию, толщина такого слоя может быть включена в глубину заложения фундамента.
3.1.9 грунт, подверженный пучению (frost-susceptible soil): Тип грунта, который может вызвать действие сил морозного пучения при его замерзании.
3.1.10 расположение теплоизоляции пола (floor insulation position): Высота нижней поверхности слоя теплоизоляции пола над поверхностью грунта.
Примечание — Если у пола нет теплоизоляции, то эту величину измеряют от поверхности пола.
3.2 Обозначения и единицы измерения
Ниже приведены основные используемые обозначения. Прочие обозначения определены там, где они использованы в тексте настоящего стандарта.
Обозначение | Величина | Единица |
В | Ширина (меньший размер) здания | м |
b | Ширина теплоизоляции грунта, измеренная от наружного края подошвы фундамента | м |
b | Ширина теплоизоляции грунта на углу | м |
b | Ширина теплоизоляции грунта вдоль стены | м |
F | Проектный индекс мороза | К·ч |
F | Индекс мороза, который статистически превышен один раз за период в n лет | К·ч |
H | Максимальная глубина промерзания нетронутого грунта без снега | м |
H | Глубина заложения фундамента для стен | м |
H | Глубина заложения фундамента для углов | м |
H | Глубина заложения вертикальной теплоизоляции | м |
h | Глубина заложения теплоизоляции пола | м |
L | Длина теплоизоляции на углах (вдоль наружной поверхности с |
Расчет подпорной стены
БАЗА ЗНАНИЙ
Задать вопрос
Категории
Статей
- ЛИРА-САПР144
- АРМ21
- Алгоритм просчета на продавливание
- Армирование композитной арматурой
- Варианты конструирования
- Информация о сочетаниях при подборе арматуры
- Конструктивный расчет ЖБ сечений
- Коэффициент длительности действия нагрузки
- Материалы для армирования колонны
- Настройки шкалы армирования
- Оболочка, Плита или Стена – что выбрать в типе армирования пластин?
- Ограничения в привязке центра тяжести арматуры
- Осреднение поперечной арматуры в пластинах
- Принятие решения об армировании плит
- Проверка на поперечную силу по п.
8.1.32 СП 63 - Произвольные классы бетона и арматуры
- Просмотр ошибок при подборе арматуры
- Расчет поперечного армирования по модели наклонного сечения
- Результаты подбора арматуры для пластин
- Создание контуров продавливание в Визор и корректировка в САПФИР
- Числовые мозаики армирования
- Чтение результатов подбора арматуры
- Чтение результатов при расчете на продавливание
- Визор30
- Варианты конструирования
- Документация — примеры расчетов
- Жесткости из МКЭ-расчета и текущие жесткости
- Жесткость КЭ грунта
- Контекстные вкладки
- Контроль приложенных нагрузок
- Копирование свойств узлов и элементов
- Локальные оси узлов
- Нагрузка на ребро пластины
- Нагрузка-штамп и её редактирование
- Объединение перемещений и АЖТ
- Признаки схемы и типы стрежневых КЭ для решения задач в ЛИРА САПР
- Прогибы плит между узлами
- Рампа — вращение образующей
- Расчетные сечения стержней
- Смена типа конечного элемента (КЭ)
- Собственный вес с коэффициентом надёжности
- Согласование осей объемных КЭ
- Согласование осей пластин
- Согласование осей стержней
- Согласование осей стержней для колонн с неточностями монтажа
- Создание объемных КЭ
- Создание одноузловых КЭ
- Сохранение задачи и результатов в ZIP-архив
- Способы применения плитных КЭ при проектировании строительных конструкций
- Строка состояния
- Суммирование нагрузок и центр сил (масс)
- Триангуляция контуров (в САПФИРе)
- Триангуляция контуров с отверстием и простого (в Визоре)
- Удаление нагрузки штамп
- Грунт13
- Взвешивающее действие воды
- Восстановление исходных нагрузок
- Высотная привязка импортированной нагрузки
- Грунтовая подушка
- Импорт данных по скважинам и характеристик грунта
- Импорт нагрузок из DXF
- Итерации для уточнения С1 и жесткостей свай
- Объединение нагрузок
- Определение расчетного сопротивления грунта основания
- Отпор грунта pz при отрыве фундамента
- Предельное напряжение растяжения грунта Rs
- Учет грунта выше подошвы фундамента
- Характеристики грунтов
- Каменные и армокаменные9
- Расчёт кирпичного простенка на косое внецентренное сжатие
- Расчёт кирпичного простенка на косое внецентренное сжатие по нелинейной деформационной модели с подбором армирования
- Расчёт на внецентренное сжатие простенка из газобетонных блоков
- Расчёт на внецентренное сжатие простенка из газобетонных блоков по нелинейной деформационной модели
- Расчёт на внецентренное сжатие простенка из керамического кирпича
- Расчёт на внецентренное сжатие простенка из керамического кирпича по нелинейной деформационной модели
- Расчёт на внецентренное сжатие простенка из силикатного кирпича
- Расчёт на внецентренное сжатие простенка из силикатного кирпича по нелинейной деформационной модели
- Расчёт на внецентренное сжатие с проверкой простенка на центральное сжатие из плоскости изгиба по нелинейной деформационной модели с подбором армирования
- Книга отчетов (документатор)2
- Видеоурок по работе с системой «Книга отчетов»
- Добавление в книгу отчетов снимков диалоговых окон
- Конструктор сечений универсальный3
- Моделирование составного сечения в конструкторе сечений
- Расчет нормальног
- АРМ21
8.1.32 СП 63Расчет нагрузки на колонну, балку, стену и перекрытие
• Элемент сжатия, то есть колонна, является важным элементом каждой железобетонной конструкции .
Они используются для безопасной передачи нагрузки надстройки на фундамент.
• В основном колонны, стойки и опоры используются в качестве элементов сжатия в зданиях, мостах, опорных системах резервуаров, заводов и многих других подобных конструкций.
• Колонна определяется как вертикальный сжимающий элемент, который в основном подвергается действующей длине и осевым нагрузкам, которые в три раза превышают ее наименьший поперечный размер.
• Элемент сжатия, эффективная длина которого меньше трехкратного его наименьшего поперечного размера, называется опорой
• Элемент сжатия, который наклонен или горизонтален и подвергается осевым нагрузкам, называется распоркой. В фермах используются подкосы.
• Функция колонн заключается в передаче нагрузки конструкции вертикально вниз для передачи ее на фундамент. Помимо стены выполняет также следующие функции:
(a) Он разделяет участки здания на различные отсеки и обеспечивает конфиденциальность.
(b) Обеспечивает защиту от взлома и насекомых.
(c) Сохраняет тепло в здании зимой и летом.
• Балка — это конструктивный элемент, который противостоит изгибу. Балка несет в основном вертикальные силы тяжести, но также тянет на нее горизонтальные нагрузки.
• Балка называется стеновой пластиной или порогом , которая переносит передачи и нагружает их на балки, колонны или стены. Он прикреплен с помощью.
• В начале века, древесные породы были наиболее предпочтительным материалом для использования в качестве балки для этой структурной поддержки цели, теперь нести силы наряду с проведением вертикальной силы тяжести, то теперь они составлены из алюминия, стали, или другие подобные материалы.
• Фактически, балки — это конструкционные материалы, которые выдерживают поперечную силу нагрузки и изгибающий момент.
• Для того, чтобы выдерживать большее напряжение и нагрузку, предварительно напряженные бетонные балки широко используются в настоящее время в фундаменте мостов и других подобных громоздких конструкций.
• Несколько известных балок, используемых в настоящее время, поддерживаются балкой, фиксированной балкой, консольной балкой, неразрезной балкой, нависающей балкой.
• Стена — структурный элемент, который разделяет пространство (комнату) на два пространства (комнаты), а также обеспечивает безопасность и укрытие.Обычно стены делятся на два типа: внешняя и внутренняя.
• Наружные стены служат ограждением для дома для укрытия, а внутренние стены помогают разделить ограждение на необходимое количество комнат. Внутренние стены также называются перегородками.
• Стены разделены жилой зоной на разные части. Они обеспечивают конфиденциальность и защиту от температуры, дождя и кражи.
Также прочтите: Что такое гипс | Тип штукатурки | Дефекты штукатурки
Что такое плита?
• Плита предназначена для создания плоских поверхностей, обычно горизонтальных, на крышах зданий, перекрытиях, мостах и других типах конструкций .
Плита могла поддерживаться стенами , железобетонными балками, обычно , монолитно отливаемыми с плитой, балками из конструкционной стали, либо колоннами , либо из земли.
• Плита — это пластинчатый элемент, имеющий глубину (D), очень маленькую по сравнению с его длиной и шириной. Плита используется в качестве перекрытия или крыши в зданиях, равномерно переносит распределительную нагрузку.
Плита может быть
• Простая опора
• Сплошная
• Консоль
Расчет различных нагрузок на колонну, балку, стену и плиту () Вес ) x Количество этажей
2) Балки = Собственная масса на погонный метр
3) Нагрузка на стену на погонный метр
4) Общая нагрузка на плиту (постоянная нагрузка + динамическая нагрузка + ветровая нагрузка + самовозраст. Вес)
Помимо указанной выше нагрузки на колонны также действуют изгибающие моменты, которые необходимо учитывать при окончательном проектировании.
Эти инструменты представляют собой упрощенный и трудоемкий метод ручных расчетов при проектировании конструкций, который в настоящее время настоятельно рекомендуется в полевых условиях.
Самый эффективный метод проектирования конструкций — это использовать передовое программное обеспечение для проектирования конструкций, такое как STAAD Pro или ETABS.
для профессиональной практики проектирования конструкций, есть несколько основных допущений, которые мы используем для расчетов нагрузок на конструкции.
Также прочтите: Введение в портальную балку | Нагрузка на портальный желоб | Тип нагрузки на козловой желоб
Расчет нагрузки на колонну:
Мы знаем, что собственный вес бетона составляет около 2400 кг / м 3 , , что эквивалентно 24.54 кн / м 3 , а собственный вес стали составляет около 7850 кг / м 3 . (Примечание: 1 килоньютон равен 101,9716 килограмму)
Итак, если мы примем размер колонны 300 мм x 600 мм с 1% стали и 2,55 (, почему так 2,55, высота колонны 3 м — размер балки ) метра стандартная высота, собственный вес колонны около 1000 кг на этаж , что id равно 10 кН.
• Объем бетона = 0.30 x 0,60 x 2,55 = 0,459 м³
• Вес бетона = 0,459 x 2400 = 1101,60 кг
• Вес стали (1%) в бетоне = 0,459 x 1% x 7850 = 36,03 кг
• Общий вес колонны = 1101,60 + 36,03 = 1137,63 кг = 11,12 кН
При проведении расчетов мы предполагаем, что собственный вес колонн составляет от 10 до 12 кН на пол.
Как рассчитать нагрузку на балку:
Мы применяем тот же метод расчета и для балки.
мы предполагаем, что каждый метр балки имеет размеры 300 мм x 600 мм без учета толщины плиты.
Предположим, что каждый (1 м) метр балки имеет размер
• 300 мм x 600 мм, исключая плиту.
• Объем бетона = 0,30 x 0,60 x 1 = 0,18 м³
• Вес бетона = 0,18 x 2400 = 432 кг
• Вес стали (2%) в бетоне = 0,18 x 2 % x 7850 = 28,26 кг
• Общий вес колонны = 432 + 28.26 = 460,26 кг / м = 4,51 кН / м
Таким образом, собственный вес будет около 4,51 кН на погонный метр.
Также прочтите: Разница между битумом и гудроном | Что такое битум | Что такое смола
Расчет нагрузки на стену :
мы знаем, что плотность кирпича варьируется от 1800 до 2000 кг / м 3 .
Для кирпичной стены толщиной 9 дюймов (230 мм) высотой 2,55 метра и длиной 1 метр ,
Нагрузка на погонный метр должна быть равна 0.230 x 1 x 2,55 x 2000 = 1173 кг / метр,
, что эквивалентно 11,50 кН / метр.
Этот метод может быть использован для расчета нагрузки кирпича на погонный метр для любого типа кирпича с использованием этого метода.
Для блоков из газобетона и блоков из автобетона (ACC), таких как Aerocon или Siporex, вес на кубический метр составляет от 550 до кг на кубический метр.
Нагрузка на погонный метр должна быть равна 0,230 x 1 x 2.55 x 650 = 381,23 кг
Если вы используете эти блоки для строительства, нагрузка на стену на погонный метр может составлять всего 3,74 кН / метр , использование этого блока может значительно снизить стоимость проекта.
Как рассчитать нагрузку на плиту :
Допустим, предположим, что плита имеет толщину 150 мм.
Таким образом, собственный вес каждого квадратного метра плиты будет
Расчет нагрузки на плиту = 0.150 x 1 x 2400 = 360 кг, что эквивалентно 3,53 кН.
Теперь, если мы рассмотрим нагрузку на чистовую отделку пола , равную 1 кН на метр , наложенная временная нагрузка составит 2 кН на метр и Ветровая нагрузка согласно Is 875 Около 2 кН на метр .
Итак, исходя из приведенных выше данных, мы можем оценить нагрузку на плиту примерно в от 8 до 9 кН на квадратный метр.
Видеоурок для лучшего понимания:
Понравился этот пост? Поделитесь этим с вашими друзьями!
Рекомендуемое чтение —
Расчетные модули
> Подпорные стены> Консольные подпорные стены
Нужно больше? Задайте нам вопрос
Вот список возможностей дизайна, содержащийся в данной Кронштейном Крепежной модуле Wall:
• Консольная стенка ствола может иметь до пяти различных секций ствола, каменных или бетонных, каждая с разной толщиной и / или размером арматуры и расстоянием между ними.Вы также можете установить на стене невесомый забор для сбора дополнительной ветровой нагрузки.
• Доплаты по обе стороны стены.
• Наклонная засыпка.
• Осевая статическая и временная нагрузка, приложенная к верхней части стены с эксцентриситетом.
• Ветер, воздействующий на выступ стены над уровнем земли.
• Добавьте поперечные нагрузки на шток — равномерные или сосредоточенные (ударные) нагрузки.
• Влияние соседнего основания за стеной, линией или точечной нагрузкой.
• Возможность использовать определяемое пользователем активное и пассивное давление или входной угол внутреннего трения, и модуль будет вычислять давления с использованием формул Ренкина или Кулона.
• Укажите процент пассивного сопротивления и сопротивления трения, которые будут использоваться для предотвращения скольжения.
• Возможность задания сопротивления скольжению с использованием сцепления вместо трения.
Схема окна
подпорной стенки модуля делит экран на левую и правую части.Левая часть содержит все входные данные (и в некоторых случаях промежуточные расчетные значения). Правая часть содержит результаты расчетов и эскизы.
ОБЩАЯ ИНФОРМАЦИЯ НА СТЕНУ
Эта вкладка позволяет ввести общую информацию, влияющую на подпорную стенку. Более конкретные данные будут введены на других вкладках, специально посвященных выносу, опоре и нагрузкам.
Сохраненная высота
Это высота удерживаемой земли, измеренная от верха опоры до верха почвы за стволом (над пяткой).Когда засыпка имеет уклон, почва будет отклоняться от этой высоты вверх и вниз. Фактическая удерживаемая высота, используемая для опрокидывания и расчетов давления на грунт, будет удерживаемой высотой, спроецированной на вертикальную плоскость задней части пятки, но для моментов штанги такое увеличение производиться не будет.
Используя вращающиеся кнопки, вы можете изменять удерживаемую высоту с шагом 3 дюйма. Вы также можете ввести любое число. После каждой записи вы можете нажимать [Tab] для перехода к следующей записи или использовать мышь для изменения положения курсора.
Высота стены над удерживаемым грунтом
Используйте эту запись, чтобы указать, выходит ли стена выше установленной высоты. Эта запись обычно используется для определения проекции «стены экрана» над удерживаемым грунтом. Эта пристройка может использоваться как невесомый «Забор» или может быть определена как секция стебля из бетона или каменной кладки без какой-либо почвы, удерживаемой за ней. Вы можете ввести ветровую нагрузку на эту проекцию, используя запись «Нагрузка @ шток над почвой» на вкладке «Нагрузки». Мы разберемся с забором, когда перейдем к экрану конструкции стержня.Общая высота стены (над опорой) будет равна удерживаемой высоте плюс высота стены над удерживаемым грунтом.
Высота почвы над носком
При измерении от верха опоры до верха почвы со стороны носка, он может варьироваться от нескольких дюймов до нескольких футов в зависимости от условий на участке. (Обратите внимание, что он указывается в дюймах.) Он используется для расчета пассивного сопротивления грунта (но его эффективная глубина может быть изменена с помощью записи «Грунт выше носка, которым можно пренебречь» в категории Сопротивление скольжению на вкладке Опоры).Эта глубина почвы также используется для расчета момента сопротивления и уменьшения чистой поперечной силы скольжения. При желании вы можете отключить последние эффекты на экране «Параметры».
Высота водного зеркала над пяткой
Если часть удерживаемой высоты находится ниже уровня грунтовых вод, активное давление насыщенного грунта возрастет ниже этого уровня. Это дополнительное давление для насыщенного грунта равно давлению воды плюс погруженный вес грунта (его насыщенный вес — 62.4) плюс надбавка почвы над уровнем грунтовых вод. Погруженный вес грунта может быть приблизительно 62% от его сухой массы.
Если вы хотите спроектировать для условий водного зеркала, введите максимальную высоту от верха основания до уровня водного зеркала. Затем модуль вычислит добавленное давление для насыщенного грунта на пяточной стороне основания, включая эффект плавучести. Он также рассчитает увеличенные моменты и срез на штоке, а также увеличенный опрокидывающий момент.Не вводите высоту, превышающую оставшуюся высоту, ни жидкость, кроме воды. Если уровень грунтовых вод находится около вершины удерживаемой высоты, может быть целесообразно ввести плотность насыщенного грунта и указать результирующее активное давление для полной удерживаемой высоты.
Уклон грунта
Можно заходить на любой откос обратной засыпки за стеной. Используйте раскрывающийся список или введите коэффициент наклона как Горизонт / Верт. Почва должна быть ровной или иметь наклон вверх. Отрицательные откосы засыпки (уклон вниз, в сторону от стены) не допускаются.
Модуль будет использовать этот наклон для:
1. включить вес треугольного клина почвы над пятой как вертикальную нагрузку, а
2. вычислить опрокидывание на основе предполагаемой вертикальной плоскости на задней поверхности основания, проходящей от нижней части основания до поверхности земли. — более крутой наклон приведет к большему опрокидывающему моменту.
При использовании метода Ренкина или Кулона окончательные расчетные давления включают влияние наклона на эти уравнения Ренкина или Кулона.
Модуль не принимает уклон засыпки круче, чем угол внутреннего трения.
Разрешить подшипник почвы
Максимально допустимое давление на грунт для статических условий. Используя кнопки вращения, вы можете увеличивать значение с шагом 50 фунтов на квадратный фут. Типичные значения варьируются от 1000 до 4000 фунтов на квадратный дюйм и более.
Плотность почвы (пятка)
Введите плотность почвы для всей земли (или воды, если применимо) выше пятки основания.Этот вес используется для расчета сил сопротивления опрокидыванию и давления грунта с учетом веса грунтового блока над выступающей пяткой основания. Когда надбавки накладываются на почву, надбавки преобразуются в эквивалентные равномерные поперечные нагрузки, действующие на стену, с помощью соотношения сила = (Нагрузка / Плотность) * Боковая нагрузка. Введите это значение в фунтах. на кубический фут. Обычные значения от 110 до 120 фунтов на фут. Больше, если почва насыщенная. Обычно предполагается, что вода составляет 64 фунта на фут.
Плотность почвы (носок)
Введите плотность почвы на носке, которая может отличаться от пяточной стороны.Когда надбавки наносятся на почву со стороны носка, надбавка преобразуется в эквивалентные равномерные поперечные нагрузки, действующие на стену, с помощью соотношения сила = (Нагрузка / Плотность) * Боковая нагрузка. Введите это значение в фунтах. на кубический фут. Типичные значения от 110 до 120 фунтов на фут.
Метод бокового давления
Здесь вы можете выбрать между E.F.P. (Эквивалентное давление жидкости), формула Ренкина или формула Кулона. В зависимости от вашего выбора метода бокового давления вам будут предложены следующие поля ввода для полного определения боковых сил, действующих на стену и основание.
Когда выбран метод EFP:
Активное давление на грунт — пятка
Введите эквивалентное давление жидкости (EFP) для удерживаемой почвы, которая опрокидывает и сдвигает стену в сторону носка. Это давление действует на шток для расчета сечения штанги, а также на общую опору + стену + высоту откоса для расчета опрокидывания, скольжения и давления грунта.
Обычно используемые значения, предполагающие угол внутреннего трения 34 °, составляют 30 фунтов на фут для ровной засыпки; 35 фунтов на уклон 4: 1; 38 фунтов на уклон 3: 1; 43 шт. Фут для уклона 2: 1; и 55 фунтов на фут 1.Наклон 5: 1. Эти значения обычно предоставляются инженером-геотехником.
Когда удерживаемый грунт наклонен, вертикальный компонент бокового давления грунта на пятку может быть приложен вертикально вниз в плоскости задней части основания. Вы можете применить эту силу для сопротивления опрокидыванию, сопротивления скольжению и / или для расчета давления на грунт, установив флажки на вкладке «Параметры».
Активное давление на грунт — носок
Введите активное давление, которое будет использоваться на носке стены.Это активное давление используется вместе со значением «Высота почвы над носком» (введенным на вкладке «Сдвиг») для расчета стабилизирующего усилия грунта на стене. Предполагается, что эта лицевая сторона стены ровная. Активное давление почвы на палец ноги противодействует активному давлению со стороны пятки, уменьшая опрокидывающую способность и чистую силу скольжения.
Это действие является спорным, поэтому по умолчанию эта сила противодействия не используется.
Пассивное давление
Сопротивление грунта перед стеной и опорой толканию для предотвращения скольжения.Его значение выражается в фунтах на фут на фут глубины (pcf). Это значение обычно предоставляется инженером-геологом. Его значение обычно варьируется от 100 до 350 фунтов на фут.
При выборе метода Ренкина или Кулона:
Угол трения грунта
Это значение вводится в градусах и представляет собой угол внутреннего трения почвы. Это значение обычно предоставляется инженером-геологом на основе испытаний грунтов, но его также можно найти в справочниках или строительных нормах и правилах для различных типовых классификаций грунта.Это значение используется вместе с плотностью почвы в стандартных уравнениях Ренкина и Кулона для определения множителей плотности «Ka» и «Kp» для получения значений активного и пассивного давления почвы.
Активное давление почвы
Это значение будет вычислено с использованием формул Ренкина или Кулона. Это представляет собой боковое давление грунта, действующее для скольжения и опрокидывания стены в сторону носка. Результат будет представлен в фунтах на квадратный фут / фут. Это давление действует на шток для расчета сечения штанги, а также на общую опору + стену + высоту откоса для расчета опрокидывания, скольжения и давления грунта.
Когда удерживаемый грунт наклонен, вертикальный компонент бокового давления грунта на пятку может быть приложен вертикально вниз в плоскости задней части основания. Вы можете применить эту силу для сопротивления опрокидыванию, сопротивления скольжению и / или для расчета давления на грунт, установив флажки на вкладке «Параметры».
Пассивное давление на грунт
Это значение также будет вычислено с использованием формул Ренкина или Кулона.Это сопротивление грунта перед стеной толканию, препятствующему скольжению. Его значение выражается в фунтах на фут на фут глубины (pcf). Общие значения обычно варьируются от 100 до 350 фунтов на фут.
ПРИКЛАДНЫЕ НАГРУЗКИ
Эта вкладка позволяет вводить все нагрузки, которые будут применены к вашей подпорной стенки в дополнение к боковому давлению на землю.
Ветровая нагрузка на обнаженный ствол над почвой
Эта сила ветра будет применяться к той части ствола, которая выступает выше удерживаемой высоты, определенной записью «Высота стены над удерживаемым грунтом».«Он используется для расчета опрокидывающего момента и скольжения, расчетного момента штока и сдвига, а также давления грунта. Следует указывать только положительные значения ветровой нагрузки. Это гарантирует, что ветровая нагрузка будет действовать в направлении активного давления грунта, увеличивая опрокидывающий момент, сила скольжения, давление на грунт, сдвиг и момент в штоке.
Вертикальная надбавка (надбавки будут учитываться как земная нагрузка, H для конструкций LRFD.)
Доплата сверх того
Эта надбавка рассматривается как дополнительный вес грунта — если надбавка составляет 240 фунтов на квадратный фут, а плотность составляет 120 фунтов на фут, то модуль использует два фута дополнительного грунта.Точно так же, если к весу плиты над основанием добавить 50 фунтов на квадратный фут, это будет эквивалентно 0,41 футам грунта (50/120). Эта надбавка повлияет на сопротивление скольжению и активное давление на палец. Помните об этом при моделировании надбавки за точечную нагрузку.
Используйте доплату TOE для сопротивления скольжению и опрокидыванию
Установка этого флажка будет включать вес покрывающего грунта на пальце ноги, чтобы противостоять опрокидыванию, и прибавлять к его весу для сопротивления трению.
Доплата за каблук
Эта надбавка считается равномерно примененной к верхней поверхности почвы над пятой.Его можно ввести независимо от того, является ли поверхность земли наклонной, но маловероятно, что дополнительная плата может применяться к наклонной засыпке. Эта надбавка всегда принимается за вертикальную силу. Эта надбавка делится на плотность почвы и умножается на активное давление для создания равномерной боковой нагрузки, прилагаемой к стене. Вы можете использовать эту дополнительную плату для предотвращения скольжения и опрокидывания, установив флажок на вкладке «Параметры». Типичные надбавки за временную нагрузку составляют 100 фунтов на квадратный фут для легкого движения и парковки и 250 фунтов на квадратный фут для движения по шоссе.
Используйте надбавку HEEL для сопротивления скольжению и переворачиванию
Установка этого флажка включает доплату за каблук. Если надбавка включает временную нагрузку, то ее использование для предотвращения скольжения и опрокидывания может быть неконсервативным. В этой ситуации рекомендуется снять этот флажок.
Вертикальная нагрузка, приложенная к верхней части штока
Эти нагрузки считаются равномерной нагрузкой по длине стены. Они наносятся на верхнюю часть самой верхней части ствола и влияют только на конструкцию стволов кладки.Статические и временные нагрузки используются для расчета проектных значений ствола и факторизованного давления реакции грунта, используемого при проектировании фундамента. Только мертвый груз используется, чтобы противостоять опрокидыванию и скольжению подпорной стенки.
Если стена подвергается высокой осевой нагрузке (скажем, более 3 тысяч фунтов / фут), это может вызвать изменение изгибающего момента в пятке. В этих условиях было бы целесообразно изучить конструкцию с высокой осевой нагрузкой и без нее, чтобы убедиться, что найдена приемлемая конструкция для всех условий.
Поскольку коэффициенты гибкости (h / t) для подпорных стенок обычно небольшие, обычно менее 10, а осевые напряжения низкие, эффекты гибкости проверяются, но обычно имеют незначительный эффект.
Если точечная нагрузка приложена к верхней части стены, например, реакция балки, то обычно предполагается, что точечная нагрузка распределяется в поперечном направлении со скоростью, которая основана на инженерной оценке рассматриваемых материалов. В результате такого распределения точечная нагрузка приведет к равномерно распределенной нагрузке некоторой относительно небольшой величины к тому времени, когда она достигнет основания штанги.Этот модуль не имеет явного поля ввода для точечных нагрузок, поэтому они должны быть представлены как равномерно распределенные нагрузки. Чтобы правильно учесть поперечное распределение, которое характерно для точечной осевой нагрузки, приложенной к стене, величина, вводимая для представления точечной нагрузки, должна учитывать этот эффект распределения. Возможно, также потребуется проверить верх стены с помощью прилагаемых расчетов на предмет локальных эффектов полной величины сосредоточенной нагрузки.
Эксцентриситет осевой нагрузки
Это эксцентриситет осевой нагрузки по отношению к центральной линии самой верхней секции штока.Положительные значения эксцентриситета перемещают нагрузку к носку, вызывая изгибающие моменты, которые добавляются к моментам, вызванным боковым давлением почвы на пятку. Отрицательные эксцентриситет не принимаются.
Вертикальная прилегающая опорная нагрузка
Эта запись дает вам возможность разместить опору (прямую или квадратную) рядом и параллельно задней поверхности стены, и ее влияние на стену будет учитываться как в вертикальных, так и в горизонтальных силах, действующих на стену и основание.Обратитесь к общей справочной схеме для определения мест, где должны производиться входные измерения.
Для «Нагрузка на линию (полосу)» вводится общая нагрузка на фут, параллельный стене (не psf). Если соседний фундамент задан как «квадратное основание» (а не линейная нагрузка), вводимая нагрузка должна быть равной нагрузке на соседний фундамент, деленной на его размер, параллельный стене, что дает значение в фунтах на линейный фут, как для непрерывной (линии) опора.
Анализ Буссинеска используется для расчета вертикального и бокового давления, действующего на шток и основание.В модуле используется уравнение (11-20a) в Bowles ‘Foundation Analysis and Design, 5th Edition, McGraw-Hill, pages 630. Когда используется анализ Буссинеска, модулю может потребоваться дополнительное время вычислений, в зависимости от скорости вашего компьютера ( после каждой записи выполняются сотни внутренних вычислений). Чтобы избежать этой задержки (которая возникает каждый раз при изменении любой записи), мы предлагаем вам использовать нулевую вертикальную нагрузку до тех пор, пока ввод данных не будет почти завершен. Затем введите фактическую нагрузку на опору и измените окончательные значения.
Для загрузки соседнего грузовика или шоссе может быть предпочтительнее использовать надбавку за пятку (единообразную) в размере 250 фунтов на квадратный фут (или более) вместо того, чтобы рассматривать ее как соседнюю опору.
Как правило, нет необходимости использовать эту функцию, если нагрузка на соседний фундамент дальше от ствола, чем сохраненная высота, за вычетом глубины соседнего фундамента ниже сохраненной высоты, так как на этом расстоянии это не окажет значительного влияния на стену .
Расстояние от стены до центральной линии основания
Это горизонтальное расстояние от центра соседнего фундамента к задней поверхности штока (измеряется в верхней части подпорной стены фундамента).Ближайший край опоры должен находиться на расстоянии не менее 30 см от поверхности стены — в противном случае рекомендуется использовать эквивалентную надбавку за пятку.
Примечания: Если расстояние по горизонтали от центра соседнего фундамента к задней поверхности штока больше, чем расстояние по вертикали от верхней части подпорной стенки фундамента в нижнюю части смежной основы, то эффект на подпорной стенке будет несущественным.
Ширина опоры
Ширина прилегающего фундамента, измеренная перпендикулярно стене.Это необходимо для создания области шириной в один фут и шириной, на которую распространяется нагрузка.
Высота основания: выше (+) или ниже (-) Оставшаяся высота
Используйте эту запись, чтобы определить нижнюю часть соседнего фундамента относительно сохраненной высоты. Ввод отрицательного числа помещает фундамент ниже удерживаемой высоты. Положительный вход обычно используется только тогда, когда почва имеет уклон, а прилегающее основание находится наверху. Чтобы вставить отрицательное число, сначала введите число, а затем нажмите знак «-» (минус).
Примечания: Если Смежно Печные еще одна удерживающей стенка на большую высоту, анализ Буссинеска может быть использован для вертикальной нагрузки, приложенной к почве от стены, однако конструкция должна также учитывать боковые (скольжения) нагрузки от этой смежной стены . Эту нагрузку можно применить как добавленную боковую нагрузку, однако это остается на усмотрение разработчика и не входит в объем модуля. При этом условии необходимо соблюдать осторожность. См. Обсуждение в сопутствующей книге: Основы проектирования подпорных стен.Для сомнительных условий почвы или площадки рекомендуется провести глобальный анализ стабильности.
Эксцентриситет
Эта запись предусмотрена в случае, если давление грунта под соседним основанием неравномерно. Введите эксцентриситет равнодействующей силы под соседним фундаментом от центральной линии соседнего фундамента. Положительный эксцентриситет смещает нагрузку в направлении переднего конца, что приводит к повышению давления на стороне, прилегающей к опоре ближайшего стволу подпорной стенки.Модуль будет использовать вертикальную нагрузку и эксцентриситет и создавать трапециевидное распределение давления под прилегающей опорой для использования с анализом Буссинеска вертикального и бокового давления.
Тип опоры
В этом поле с раскрывающимся списком можно ввести либо изолированное основание с помощью выбора «Прямоугольная опора», либо сплошное основание с использованием выбора «Линейная нагрузка».
Коэффициент Пуассона
Поскольку результирующие давления чувствительны к коэффициенту Пуассона, имеется запись, позволяющая выбрать коэффициент от 0.30 до 0,55. Это значение должен предоставить инженер-геотехник. Часто предполагается значение 0,50.
Боковая нагрузка на шток
Этот ввод позволяет вам указать дополнительную равномерно распределенную боковую нагрузку, приложенную к штоку.
Это для точечной нагрузки, например, от удара автомобиля или аналогичной силы. Введите нагрузку с шагом в один фут, разделив «Высота до низа» и «Высота до верха» на полфута (или метр).
Примечание. Эта нагрузка не учитывается. Чтобы применить коэффициент нагрузки (например, для ударной нагрузки), пропорционально увеличьте прилагаемую нагрузку (например, ударная нагрузка в 1000 фунтов, требующая коэффициента нагрузки 2,0, будет введена как 2000 фунтов). Вам может потребоваться выполнить несколько расчетов для проверки комбинаций коэффициентов нагрузки.
Имейте в виду, что при рассмотрении сосредоточенной боковой нагрузки можно уменьшить ее величину, чтобы учесть тот факт, что нагрузка распределяется по горизонтали на уровнях ниже точки приложения.
Высота до верха
Этот размер определяет верхнюю степень дополнительной поперечной нагрузки, измеренную от верха основания. Не вводите размер, который превышает «удерживаемую высоту» плюс «высоту стены над удерживаемым грунтом».
Высота до низа
Этот размер определяет нижний предел (или нижнюю часть) добавленной боковой нагрузки, измеренный от верха основания.
ВКЛАДКА ДИЗАЙНА STEM
Материал
Используйте кнопки, чтобы выбрать Каменную кладку, Бетон или Забор.Забор разрешен только на стене, превышающей установленную высоту, и считается невесомым.
Толщина
Используйте раскрывающийся список для ввода толщины стенки. Если выбрана кладка, вам будет предоставлена стандартная толщина кладки (например, 6 дюймов, 8 дюймов, 12 дюймов). Если выбран бетон, вы можете увеличить шаг с шагом в один дюйм. Если выбран вариант «Забор», эта запись недоступна, так как ограждение считается невесомым.
Вес стены
Это отображаемое значение основано на данных стены, введенных ранее.Для бетонных стержней удельный вес бетона можно указать на вкладке «Стержень». Для стеблей каменной кладки предполагается затирка 140 фунт-фут, а удельный вес готовой ствола зависит от указанной толщины, типа CMU и состояния флажка Solid Grouting, которые находятся на вкладке «Стержень». На вкладке «Параметры» также доступен множитель для изменения табличных значений веса каменных стен.
Стандартные промышленные значения веса единицы кладки, используемые этим модулем, можно изменить, щелкнув Базы данных> Данные бетонной единицы кладки в главном меню, а затем нажав кнопку [Изменить].
Метод расчета
Когда выбирается секция ствола кладки, это позволяет выбрать методы ASD или LRFD. Когда выбирается последнее, входные обозначения меняются (например, fs на fy), и все вычисления основаны на LRFD.
Размер арматуры
Сделайте выбор из раскрывающегося меню для размеров стержней от №3 до №10. Размеры «Soft Metric» будут отображаться в скобках рядом.
Положение арматуры
Выберите между центром или краем.Если выбран вариант «Центр», расстояние d арматурного стержня будет 1/2 фактической толщины стенки. Если выбрано Edge, он будет расположен на пятке ножки.
Для проектирования каменной кладки модуль содержит таблицу соответствующих значений «d», которые можно использовать для блоков различных размеров и расположения центра / краев, как показано в таблице ниже.
Глубина позиции арматуры для кладки, значения по умолчанию.
Номинальная толщина
Глубина арматуры (дюймы)
Центр
Край
6 «
2.75 «
2,75 дюйма
8 «
3,75 дюйма
5,25 дюйма
10 «
4,75 дюйма
7,25 дюйма
12 «
5,75 дюйма
9,0 «
14 «
6.75 «
11,0 «
16 «
7,75 дюйма
13,0 «
Для бетона глубина краевого арматурного стержня всегда равна толщине стержня менее 1,5 дюйма для стержней № 5 и меньшего размера (или 2 дюйма для стержней № 6 или больше), минус половина диаметра стержня.
Поле указания позиции
Щелкните это поле, чтобы изменить значение «d» по умолчанию.
Fs
Введите допустимое напряжение стали, основанное на расчетном рабочем напряжении, которое следует использовать для расчета секции ствола кладки. Кнопка вращения изменяет это значение с приращением и не отображается, если указана бетонная стена.
Краткосрочное увеличение
Этот коэффициент применяется к конструкции ASD каменной кладки и допустимой нагрузке на грунт, как это разрешено IBC 2009, раздел 1806.1, и ACI 530-08, раздел 2.1.2.3. Это применимо только при воздействии ветра и / или сейсмических воздействий.
Сплошной раствор
Это относится только к кладке. Если этот флажок установлен, вес стены будет основан на стандартном промышленном весе твердого раствора для легкого, среднего или обычного веса блока, независимо от указанного расстояния между армированием. Если этот флажок не установлен, модуль будет рассчитывать вес, исходя из предположения, что залиты только ячейки, содержащие арматуру.
Это также влияет на эквивалентную толщину твердого тела для расчета сдвига стержня и площадь для расчета осевого напряжения (в сочетании с моментом для стержней каменной кладки).
Модульный «n», коэффициент
Это множитель, используемый для расчета модуля упругости кладки. Оба ACI 530-05 и ACI 530-08 указывают Em = 900 * f’m, что является значением по умолчанию. Множитель можно изменить на вкладке «Параметры».
Эквивалентная толщина твердого тела
При частичном заполнении раствором (не сплошным раствором) это значение создается из внутренней базы данных, доступ к которой можно получить, щелкнув База данных> Данные бетонной кладки.
Высота конструкции штока
ВАЖНО! Термин «Расчетная высота штанги», используемый в этом модуле, означает высоту над верхом основания (т.е. над основанием штанги). Это высота над нижней частью стержня, на которой модуль должен рассчитывать моменты и сдвиги.
Вы можете разделить шток на пять частей (с шагом в высоту). Каждая секция представляет собой либо другой материал (бетон, кладка или забор), либо изменение толщины, либо изменение размера арматуры или расстояния между ними.
Для большинства стен используются только две или три смены секций ствола. Например, было бы логично создать изменение сечения в верхней части дюбелей, выступающих в стойку от основания, и, возможно, другое изменение сечения дальше по стене, где требуется более экономичный дизайн.
низ
Вы должны начать проектирование штока здесь, в основании (высота над опорой = 0,00), где момент штока и усилие сдвига максимальны.По мере того, как вы манипулируете размерами стержней, расстоянием между ними и положением (сначала вы, конечно, выбираете материал стены и пробную толщину), пока в поле Сводка не появится приемлемый коэффициент напряжений (чем выше и ближе к 1,0, тем эффективнее) .
Чтобы проверить стену на более высокой проектной высоте, например, на расстоянии не менее LAP REQ’D IF ABOVE, где армирование или толщина может быть уменьшена, нажмите кнопку [Insert Stem] и войдите в следующий более высокий раздел. Переместите кнопку вращения на желаемую высоту над верхом основания или введите ее, набрав.Это переместит (и затемнит) нижнюю секцию, и теперь вы можете создать новую секцию.
Продолжайте таким же образом, нажимая кнопку [Вставить шток] после завершения проектирования каждой секции штанги, максимум до пяти высот. Новую расчетную высоту следует вводить только тогда, когда вы хотите изменить материал, толщину или арматуру, и она никогда не должна быть меньше двух футов.
ПОДНОЖКА
Ширина носка
Ширина носка опоры, измеряется от переднего края опоры до передней поверхности ствола.Может быть установлено значение 0,00 для условия линии собственности. Все опрокидывающие моменты и моменты сопротивления относятся к нижнему переднему краю зацепа.
Ширина каблука
Расстояние от передней поверхности ножки до задней части выступа пятки. Если введен размер, который меньше ширины ножки у основания, модуль автоматически сбросит размер пятки, по крайней мере, на ширину ножки. Для линии собственности на задней поверхности штанги этим размером будет ширина штанги.
Общая ширина
Расчетная ширина подошвы, ширина носка + ширина пятки.
Толщина
Общая толщина опоры, НЕ включая глубину шпонки (если используется). При расчете фундамента на изгиб и сдвиг глубина арматурного стержня «d» принимается как Глубина опоры — покрытие арматурного стержня — ½ дюйма (для учета радиуса арматурного стержня). Если толщина основания недостаточна для прочности на сдвиг, появится красный индикатор предупреждения.
Толщина фундамента должна быть достаточной для обеспечения развития арматуры (для крючковидных дюбелей) и покрытия арматуры (рядом с почвой).Если вы введете размер меньше, чем требуется для развития стержневой штанги, в верхней части экрана появится красное сообщение. Если толщина недостаточна, увеличивайте толщину фундамента или меняйте дюбели штока, пока это сообщение не исчезнет.
f’c
Введите сжимающее напряжение бетона для опоры.
Fy
Допустимый предел текучести арматуры для расчета изгибной арматуры фундамента.
Плотность опоры
Эта опция необходима, так как в случае возникновения эффекта плавучести она снизит эффективный вес бетонного основания.
Мин. Соотношение «As»
Введите абсолютный минимальный процент стали, который будет использоваться для расчета требований к расстоянию между стержнями (обычно 0,0018 Ag для Fy = 60 000 фунтов на кв. Дюйм, но применимость кода для опор спорна). Если% стали, требуемое для анализа напряжения, меньше 200 / Fy, минимум (200 / Fy или 1,333 * требуемый процент изгиба) вычисляется и сравнивается с введенным здесь Minimum As%, и большее из двух значений используется для рассчитать требования к расстоянию между стержнями.
Глубина ключа
Глубина шпонки ниже основания опоры. Нижняя часть ключа используется в качестве нижней горизонтальной плоскости для определения размера блока пассивного давления от почвы перед основанием. Отрегулируйте эту глубину так, чтобы коэффициент безопасности скольжения был приемлемым (обычно используется значение 1,5).
Ширина ключа
Ширина шпонки, измеренная в том же направлении, что и ширина основания. Обычно это 12-14 дюймов, но обычно не менее половины глубины клавиши, поэтому изгибное напряжение в ключе обычно минимально.
Расположение ключа
Введите расстояние от переднего края мыска до начала шпонки. Не вводите расстояние больше, чем ширина основания минус ширина шпонки.
Метод сопротивления скольжению
Укажите, будет ли сопротивление скольжению обусловлено трением и пассивным давлением или сцеплением и пассивным давлением.
Земля до пят, не обращать внимания
Поскольку почва над носком основания может быть рыхлой и неуплотненной, она может иметь небольшое пассивное сопротивление или не иметь его.Эта запись дает вам возможность игнорировать любую или всю высоту почвы над носком, которую вы ввели на вкладке «Критерии». При желании можно пренебречь почвой по зацепу плюс толщиной подошвы.
Ftg / коэффициент трения грунта
Введите здесь коэффициент трения. Обычно он предоставляется инженером-геологом и обычно варьируется от 0,25 до 0,45.
% ТРЕНИЕ, используемое для сопротивления скольжению
Это может быть указанное ограничение в геотехническом отчете.Введите значение от нуля до 100%.
% ПАССИВНЫЙ Используется для сопротивления скольжению
Это может быть указанное ограничение в геотехническом отчете. Введите значение от нуля до 100%
Боковые силы у основания опоры
Это общая боковая сила, действующая на ствол и основание, которая заставляет стену скользить и которой необходимо сопротивляться. Это общее активное давление со стороны пятки за вычетом активного давления со стороны носка.
минус пассивная сила давления
Здесь используется допустимое пассивное давление в pcf, умноженное на доступную глубину (толщина основания плюс грунт над носком минус высота, которую следует пренебречь), и умноженное на процент полезного использования, который вы указали, для вычисления общего пассивного сопротивления.Также будет добавлен вес из-за надбавки за носк, если применимо. Если используется ключ, доступная глубина пассивного давления будет до нижней части ключа.
меньше сила трения
Это общая вертикальная реакция, умноженная на коэффициент трения и умноженная на указанный вами процент использования.
Требуется дополнительная сила сопротивления
Если это 0,0 фунта, силы уравновешиваются, но может не быть запаса прочности. Следите за скользящим фактором безопасности, чтобы получить адекватное значение (обычно 1.5). При необходимости подумайте о добавлении шпонки или изменении размеров фундамента.
Дополнительная сила, необходимая для 1,5-кратного запаса прочности
Это дополнительная сила сопротивления, которая потребуется для достижения коэффициента безопасности 1,5. Если это значение равно нулю, то коэффициент безопасности скольжения уже больше или равен 1,5.
Крышка арматуры в области пятки и носка
Эти поля ввода позволяют указать прозрачное покрытие, которое будет использоваться на пятке и на носке.При указании этих значений имейте в виду, что арматурный стержень с носком размещается ближе всего к нижней части основания, а арматурный стержень с пяткой располагается ближе всего к верху основания. При вычислении размера «d» для расчетов прочности на изгиб и сдвиг этот модуль будет учитывать толщину основания, а затем вычесть указанную прозрачную крышку и дополнительные 1/2 дюйма для учета радиуса арматурного стержня.
Опции усиления носка
В этом списке представлены варианты размеров арматуры и расстояния для нижних пальцевых стержней.Обычно упоры для пальцев являются продолжением стержневых дюбелей, которые загнуты к носку. Следовательно, может быть наиболее эффективным просто проверить, что размер стержня и расстояние, используемое для стержневых дюбелей, находятся в пределах диапазона выбора, предлагаемого для вариантов усиления носка.
ПРИМЕЧАНИЕ: Если появляется сообщение «Нет необходимости в армировании», это означает, что изгибная способность основания (модуль разрыва, умноженный на модуль упругости сечения, с вычетом 2 дюймов из толщины для допуска на трещину в соответствии с кодом) достаточна для сопротивления прикладной момент.Однако в некоторых случаях проектировщик может счесть целесообразным добавить арматуру независимо от теоретической прочности на изгиб. Для обычного бетона согласно ACI 22.5.1, Fr = phi (5) (f’c) 1/2, где phi = 0,55.
Варианты усиления пятки
В этом списке представлены варианты приемлемых размеров и расстояния между планками верхней пятки. Желательно выбрать интервал, который является модульным с дюбелями стержня для простоты конструкции. Примечание: модуль не рассчитывает развернутую длину пяточной перекладины внутрь от задней поверхности стержня (где момент максимален).
ПРИМЕЧАНИЕ: Если появляется сообщение «Нет необходимости в армировании», это означает, что изгибная способность основания (модуль разрыва, умноженный на модуль упругости сечения, с вычетом 2 дюймов из толщины для допуска на трещину в соответствии с кодом) достаточна для сопротивления прикладной момент. Однако в некоторых случаях проектировщик может счесть целесообразным добавить арматуру независимо от теоретической прочности на изгиб.
ТАКЖЕ ПРИМЕЧАНИЕ: Расчетный момент пятки может зависеть от настройки, используемой для пункта «Пренебрегать восходящим давлением на пятку для Ftg M & V» на вкладке «Параметры».Дополнительную информацию см. В разделе на вкладке «Параметры».
Варианты усиления ключа
Если натяжение при изгибе недостаточно для сопротивления изгибу шпонки, появится сообщение, указывающее на необходимость армирования. Вы можете изменять ширину клавиши, пока сообщение не исчезнет. Если требуется армирование, параметры будут показаны на вкладке «Опора».
ВКЛАДКА ОПЦИЙ
Используемое активное давление носка
В этом поле с раскрывающимся списком можно указать, должен или не должен модуль прикладывать горизонтальное активное давление со стороны носка для уменьшения опрокидывающего момента и силы скольжения, которой необходимо противодействовать.Обычно это НИКОГДА не используется. Он был добавлен, чтобы помочь в тех случаях, когда основание было очень глубоко зарыто в землю.
Плита противостоит всем силам скольжения
Установите этот флажок, когда плита находится перед стеной для сопротивления боковому скольжению. Когда этот флажок установлен, скольжение не является проблемой конструкции — пассивное сопротивление и сопротивление трения игнорируются — но боковая сила скольжения отображается для проверки сопротивления, оказываемого плитой.
Предполагается, что плита находится наверху фундамента, а не выше, поэтому установка этого флажка не приведет к уменьшению расчетного сдвига или момента в штоке.
Пренебрежение повышением давления на пятке для Ftg M&V
Когда пользователь отменяет опцию «безнадзорности повышающего давления на пяте для Footing Moment и Shear»:
• Программа учитывает давление вверх в пятке.
• Восходящее давление снижает момент, вызванный весом почвы и собственным весом пятки.
• Программа сообщает о фактическом чистом моменте в пятке.
Когда пользователь выбирает опцию «безнадзорности повышающего давления на пяте для Footing Moment и Shear»:
• Программа НЕ учитывает восходящее давление пятки.
• Программа определяет момент пятки, обусловленный весом почвы и собственным весом пятки.
• Затем программа применяет следующую логику:
— Расчетный момент пятки является консервативным, если пренебречь направленным вверх давлением на пятку.
— Расчетный момент пятки будет действовать в том же направлении, что и момент носка.
— Сумма момента пятки и момента носка не может быть больше расчетного момента стержня, который в первую очередь передает момент этому суставу.
— Таким образом, программа консервативно предполагает, что расчетный момент пятки — это расчетный момент пятки, но не превышающий расчетный момент выноса.
Используйте раздел 2010 CBC 1807.2.1
Раздел 1807.2.1 2010 CBC и IBC 2009 требует, чтобы проектировщик учитывал при расчете скольжения влияние активного давления, распространяющегося полностью до дна шпоночной канавки, когда она используется.Выбор этой опции гарантирует, что анализ должным образом учитывает полную степень активного давления на шпоночную канавку.
Варианты использования вертикальной составляющей активного давления
Вертикальный компонент бокового давления прикладывается в вертикальной плоскости к задней части пятки. Вы можете выбрать, использовать ли эту силу для предотвращения опрокидывания, сопротивления скольжению и уменьшения давления почвы на грунт.
Если вы выберете вариант использования этой силы для сопротивления опрокидыванию, то для ровной обратной засыпки модуль выполнит обратное вычисление метода EFP, чтобы найти эквивалентный угол внутреннего трения, а затем применит этот вертикальный компонент, равный tanß.Если бы был выбран метод Ренкина или Кулона, эта вертикальная составляющая была бы касательной к.
Если вы выберете вариант использования этой силы для сопротивления скольжению, то расчет скольжения будет включать дополнительную силу трения, которая может быть создана в результате дополнительной вертикальной силы.
Если вы выберете опцию «Давление на грунт», то влияние этого вертикального компонента на задней части пятки будет учитываться при расчете давления на грунт.
Коэффициент
, применяемый к кладке для расчета Em
Модуль упругости кладки составляет 900 раз f’m согласно ACI 530-05. Это поле позволяет при необходимости ввести множитель, отличный от 900.
Множитель, применяемый к весу CMU из таблиц
Эта запись позволяет вам увеличивать или уменьшать внутренние значения по умолчанию весов CMU, как показано на вкладке Stem.
Факторы нагрузки
Для каждого типа нагрузки (DL, LL и т.д.) будет отображаться коэффициент по умолчанию.Вы можете изменить их и установить новые значения по умолчанию, но не забудьте просмотреть их на предмет нового дизайна, поскольку они могли быть изменены.
ВКЛАДКА РЕЗУЛЬТАТОВ
Коэффициенты устойчивости
Отображаются как для опрокидывания, так и для скольжения.
Давление на грунт на носке и пятке
Это результирующее необработанное давление почвы на палец и пятку. Если эксцентриситет находится за пределами средней трети, давление пятки будет равно 0.00. (Примечание: когда результат находится за пределами средней трети, модуль вычисляет давление на палец, предполагая отсутствие напряжения на пятке).
Допустимое давление почвы
Это для справки в качестве ввода на вкладке «Критерии».
Общая нагрузка на подшипник
Это сумма всех вертикальных сил.
Результирующий эксцентриситет
Расстояние от центра опоры до результирующего давления почвы.
Эксцентриситет внутри / вне средней трети
Результат находится за пределами средней трети ширины основания, если эксцентриситет больше одной шестой ширины основания.(Если за пределами средней трети, модуль вычисляет давление грунта на палец, предполагая отсутствие напряжения в пятке.)
Фактор давления почвы по ACI на носке и пятке
Коэффициенты нагрузки применяются ко всем постоянным и временным нагрузкам для определения общей вертикальной нагрузки для давления грунта, используемой при расчете опорных моментов и сдвигов. Затем эта нагрузка применяется с тем же эксцентриситетом, который рассчитан для давления грунта при эксплуатационной нагрузке, чтобы получить фактические значения давления грунта для расчета опор с использованием принципов расчета предельной прочности.Обратите внимание, что, поскольку только факторизованные вертикальные нагрузки применяются к результирующему эксцентриситету без факторизации, истинный коэффициент нагрузки 1,6, применяемый к боковому давлению грунта, не используется при проектировании фундамента. Если бы эксцентриситет результирующей вертикальной нагрузки рассчитывался с использованием факторных нагрузок, расстояние не могло бы действительно отражать правильное состояние напряжения в почве. Коэффициенты нагрузки ACI предназначены для получения консервативных результатов для стресса. Расчет эксцентриситета факторизованной нагрузки дает диаграммы давления почвы, которые не всегда отражают фактическое распределение давления почвы под основанием, и дают необоснованные результаты.Тем не менее, при проектировании бетонной штанги всегда используется факторное боковое давление грунта.
Mu Design @ носок / каблук
Это усиленные (1,2) моменты на лицевой стороне выноса для моментов пальцев и пяток. Поскольку ни один из них не может быть больше, чем базовый момент штока (учитывается, если шток бетонный), последний может иметь значение. Эти моменты будут уменьшены, если вы решите пренебречь восходящим давлением почвы на вкладке «Параметры».
В сообщении будет указано, какие элементы управления.
Сдвиг на носке и пятке
Фактический сдвиг рассчитывается исходя из одностороннего действия в основании на расстоянии «d» (толщина подошвы — покрытие арматуры) от передней части нижней секции штока и на лицевой стороне штока со стороны пятки. Если «d» больше, чем выступающая длина носка или пятки, то односторонний сдвиг равен нулю.
Допустимое срезание опоры
Допустимая единица сдвига равна (0,75 * 2 * f’c½).
RSM — ТАБЛИЦА УПРАВЛЯЮЩИХ МОМЕНТОВ
На этом экране в табличной форме представлен каждый компонент, влияющий на момент сопротивления, с указанием веса и плеч рычага от переднего края зацепа до центра тяжести груза.
Для вычисления вертикальной составляющей, если этот флажок установлен на экране ОПЦИИ и если был выбран метод EFP, модуль будет выполнять обратное решение с использованием формулы Ренкина для получения эквивалентного угла внутреннего трения.
Сила и момент, отображаемые внизу, учитывают эффект вертикального компонента, если установлен флажок на вкладке «Параметры».
OTM — ВКЛАДКА ПЕРЕВОЗКИ
На этом экране в табличной форме представлен каждый компонент, действующий горизонтально, переворачивая систему стен / фундаментов.Центроид каждой силы умножается на расстояние до нижней части основания. Активное давление пятки включает в себя влияние дополнительных нагрузок и уровня грунтовых вод, если применимо, и его расстояние до центра тяжести общей поперечной силы.
Отображается полный опрокидывающий момент вместе с коэффициентом сопротивления / опрокидывания. Момент опрокидывания уменьшается за счет активного давления со стороны носка, если этот параметр выбран на вкладке «Параметры».
РАЗДВИЖНАЯ ВКЛАДКА
ШТОК
ВКЛАДКА С ЭСКИЗОМ
ЗАГРУЗКА
Задачи лестничной диаграммы
Что такое лестничная задача?
Задача лестницы — это задача, связанная с лестницей.
Две задачи являются классическими, проблема лестничной коробки (рисунок)
и проблема скрещенных лестниц.
Они особенные, потому что проблема простая, но
расчет усложняется.
Проблема со стеной лестницы
сверху
Следующую задачу можно найти в школьной книге в
связь с теоремой Пифагора.
…… 1-я проблема:
Лестница длиной c = 7м прислоненная к
стена с основанием d = 1.4 м от стены у основания. На какой высоте
лестница касается стены?
Решение: c² = h² + d², следовательно, h = sqrt (c²-d²) = sqrt (7²-1,4²) m = 6,9 м.
Результат: лестница касается стены на высоте 6,9 м.
Когда функция косинуса
вводится, вы можете найти угол наклона.
Имеется cos (alpha) = d / c. Тогда вы получите alpha = arc cos (d / c) = arc
cos (1,4 / 7) = 78,5 °.
Проблема с лестничной коробкой
сверху
Если вы говорите о проблеме лестницы, вы обычно имеете в виду
следующая проблема.
…… 2-я проблема:
Ящик в форме куба с краем
длиной 1м стоит перед стеной. Лестница длиной 5 м опирается на
стены и просто касается коробки краем. Как высоко на стене
наверху лестницы?
Два решения …… Очевидно, есть два способа опереться на лестницу
у стены. Вы часто спрашиваете максимальную высоту, поэтому проблема
только одно решение. Подразумевается лестница с более крутым положением. Этот
более реально.
Формула …… Неразумно указывать высоту у стены и
расстояние от ступни лестницы от стены в качестве переменных. Расчет проще с x и y из-за
симметрия по этим переменным.
Есть два уравнения:
Теорема Пифагора гласит (#) c² = (b + x) ² + (b + y) ².
Есть два похожих треугольника (желтые), и у вас
(##) x : b = b : y.
Если вы изолировали y в (##) и поместили y в (#), вы получите c² = (b + x) ² + (b + b² / x) ²
или x 4 + 2bx³ + (2b²-c²) x² + 2b³x + b 4 = 0.
Это уравнение 4-й степени.
Приблизительно
решение
Имеется b = 1 и c = 5. Это приводит к уравнению x 4 + 2x³-23x² + 2x + 1 = 0.
Вы найдете приблизительное решение, исследуя
график функции f (x) = (x 4 + 2x³-23x² + 2x + 1) / 64
и найдя точки на оси абсцисс.Коэффициент 1/64 произвольный и
делает возможным красивый график.Высота лестницы 3,84 м + 1 м = 4,84 м при x = 0,26.
и y = 1 / x = 3,84.
Или высота лестницы 1,26 м при x = 3,84 и
у = 1 / х = 0,26.
точно
решение
Вы можете использовать p-q-формулу квадратного уравнения
решить x 4 + 2x³-23x² + 2x + 1 = 0.
Сначала вы кладете c = 5 и b = 1, а затем y = 1 / x. В уравнение
(#) c² = (x + b) ² + (y + b) ².
Вы получаете (x + 1) ² + (y + 1) ² = 25 или (x + 1) ² + (1 / x + 1) ² = 25
или x² + 2x + 1 + 1 / x² + 2 / x + 1 = 25 или [x² + 2 + 1 / x²] + [2x + 2 / x] = 25.
Имеются z² = x² + 2 + 1 / x² и 2z = 2x + 2 / x. с
г = х + 1 / х.
Таким образом, вы получаете квадратное уравнение относительно z: z² + 2z = 25 = 0.
Дальнейший расчет:Результат: лестница достигает высоты 4,84 м или 1,26 м.
Решение с помощью
тригонометрические формулы, присланные Каваном Оруэллом …… Проблема описана снова
Имеется лестница длиной c, прислоненная к вертикали.
стена.Он просто касается угла квадратной коробки размером b x b.
Какова высота лестницы до стены?
Обратите внимание на угол t в этом решении.
Пусть b = 1 и c = 5.
Вы получаете 5 = 1 / sin (t) + 1 / cos (t), потому что
похожих треугольников
и 5 = [sin (t) + cos (t)] / [sin (t) cos (t)]
порядок 5 [sin (t) cos (t)] = sin (t) + cos (t).
Есть тригометрическая идентичность
sin (2t) = 2 sin (t) cos (t).
Тогда существует 2,5sin (2t) = sin (t) + cos (t).
Возведение в квадрат дает 6,25sin² (2t) = [sin (t) + cos (t)] ² = sin² (t) + 2sin (t) cos (t) + cos² (t) = 2sin (t) cos (t) +1
потому что sin² (t) + cos² (t) = 1.
Это дает 6,25sin² (2t) = sin (2t) +1.
Это квадратное уравнение в
sin (2t) = y, 6,25y² = y + 1 или y²-0,16y-0,16 = 0.
Есть решения y 1 = 0,08 + sqrt (0,1664)
и y 2 = 0,08-sqrt (0,1664).
y = sin (2t) дает
sin (2t 1 ) = 0,08 + sqrt (0,1664) или 2t 1 = 29,20 °
или 2t 2 = 180 ° -29,2 ° = 150,80 °.
Формула h = c * sin (t) дает h 1 = 5 * sin (t 1 ) = 5 * sin (14.60 °) = 1,26
или ч 2 = 5 * sin (t 2 ) = 5 * sin (75,40 °) = 4,84 .
Решение y 2 = 0,08-sqrt (0,1664) есть
отрицательный и ведет к углам, которые невозможны для лестницы.
Варианты
> Вы можете искать целые числа как решения
уравнения 4-й степени.
> Вы можете заменить куб на
твердый.
> Вы можете рассчитать соотношение как
лестница разделена на две части. …… > Можно куб сжать.
Тогда вы можете интерпретировать лестницу
задача как расчет треугольника.
Задайте сторону c, угол гаммы
и биссектриса w гамма в произвольном треугольнике.
Найдите сторону a.
Имеется гамма = 90 ° для
проблема лестницы.
Подробнее об этой задаче лестницы
на домашней странице Торстена Силлке (URL-адрес ниже).
Здесь вы также обнаружите, что Ньютон даже работал
по проблеме «отрезок в углу». Кент Холинг (2) поднял вопрос, когда и где
задача «Задача с одной лестницей» возникла впервые.
«Самая старая известная нам ссылка на проблему квадратного ящика.
датируется 1754 годом. (Томас Симпсон: Трактат по алгебре, Джон Норс, Ломндон
1745, стр. 250). Самая старая известная нам справочная информация по общей проблеме коробки
с 1907 г. (А.Сирил Пирсон: Стандартная книга-головоломка двадцатого века,
George Routledge & Sons, Ltd., Лондон, 1907 г., стр. 103.) »
Проблема угла лестницы
сверху
…… 3-я проблема:
Имеется лестница длиной
c и коридор шириной b. К сожалению, коридор имеет право
угловой изгиб. Какой длины может быть лестница, чтобы ее можно было перемещать по
угол?
Это максимальная проблема.Длина лестницы c (или
c² для расчетов) должно иметь максимальное значение.
…… Теорема Пифагора приводит к (#) c² = (x + b) ² + (y + b) ².
Имеется (##) ist y : b = b : x или y = b² / x
из-за похожих желтых треугольников. .
Если вы замените y на (#), вы получите функцию c² = (x + b) ² + (b² / x + b) ²
или c² = x² + 2bx + b 4 / x² + 2b³ / x + 2b².
Первая производная: (c²) ‘= 2x + 2b-2b 4 / x³-2b³ / x².(Вторая производная положительна при x> 0)
(c²) ‘= 0 приводит к уравнению 4-й степени x 4 + bx³-b³x-b 4 = 0.
Вы легко узнаете, что x = b — решение.
x = b приводит к c / 2 = sqrt (b) или c = 2sqrt (2) b. Это решение
показано на рисунке выше.
Результат: Лестница длиной c = 2sqrt (2) b является
самый длинный.
Более общее решение —
прислал Йохан Асма Удобно ввести переменную be p, так что
b + pb = (1 + p) b — отрезок горизонтальной линии.
Тогда существует x: (a + x) = b: [(1 + p) b] или x = a / p. Теорема Пифагора дает c² = (a + a / p) ² + (b + pb) ²
или c² = a² (1 + 1 / p) ² + b² (1 + p) ²
или c² = a² (1 + 2 / p + 1 / p²) + b² (1 + 2p + p²).
Вы ищите значение p так, чтобы c = c (p) было минимумом.
Вам нужна первая производная c ‘или попроще (c²)’ = a² (-2 / p²-2 / p³) + b² (2 + 2p).
(c²) ‘= 0 дает a² (-2 / p²-2 / p³) + b² (2 + 2p) = 0
или a² (-2p-2) + b² (2p³ + 2p 4 ) или -2a² (p + 1) + 2b²p³ (1 + p)
или (-2a² + 2p³b²) (p + 1) = 0.
Решение: p³ = a² / b² или p = (a / b) 2/3 .
Пусть b = a. Тогда p = 1 и c² = a² (1 + 2 / p + 1 / p²) + b² (1 + 2p + p²) = b² (1 + 2 + 1) + b² (1 + 2 + 1) = 8b².
или c = 2sqrt (2) b.
Так же проблему можно дать
как проблема с лестницей:
Ящик в форме куба с краем
длиной 1м стоит перед стеной. Лестница прислоняется к стене и
просто касается коробки краем. Какова самая короткая лестница?
Ханс-Иоахим
Саймон прислал мне следующее решение.
Переходные лестницы
Проблема наверх
Мартин Гарднер (1) опубликовал следующую задачу и
он стал популярным. Начать решение легко, но тогда оно будет выглядеть как
сложно, как проблема с лестницей.
…… 4-я проблема:
Между двумя лестницами две
дома.
Как долго расстояние x между
стены дома, если длина лестниц a и b и высота c
над землей перехода даны?
Попытка
решения Вы вводите четыре переменные h, k, y и z (рисунок) Имеется (#) y: c = x: h и z: c = x: k из-за похожих треугольников.
Уравнения произведения: yh = cx и zk = cx.
Теорема Пифагора приводит к (##) a² = x² + h²
и b² = x² + k².
Тогда есть (###) x = y + z
Изолируйте h и k в (##) и сначала замените их в (#)
а затем в (###). Вы получаете:
Если вы хотите удалить корни, вы должны возвести уравнения в квадрат
дважды.
Тогда вы получите уравнение 8-й степени :-(.
Решение
как замена
Вы не рассчитываете расстояние до стены напрямую
но через высоту h более длинной лестницы. Вы получаете 1 = c / h + c / k и k = ch / (h-c) с (#) и (##).
(##) дает a²-h² = b²-k².
Если вы замените k = ch / (h-c) на a²-h² = b²-k²,
вы получите h 4 -2ch 3 — (a²-b²) h² + 2c (a²-b²) h-c² (a²-b²) = 0
после нескольких шагов.
Пример с числами
…… Вы рисуете лестницы a = 8,0 и b = 7,0 между двумя
стены шириной x = 5. Тогда c = 2,8.
Блок может быть высотой 1 м для лестниц. Тогда уравнение 4-й степени имеет вид
h 4 -5,6h 3 -15h² + 84h-117,6 = 0.
Принадлежащая ему функция
f (h) = (h 4 -5,6h 3 -15h² + 84h-117,6) / 256.
На графике от h = 0 до f (x) = 0. Тогда теорема Пифагора
приводит к x = 4,9.
……
Результат: Чертеж и расчет дают примерно одинаковые результаты.
Привлечение проблемы в рекреационной
математика не в том, чтобы определить расстояние до стен дома.Это вызов
найти целых чисел в качестве значений и как можно меньших целых чисел
для разной длины.
Вы найдете коллекцию в книге Гарднера.
Кент Холинг (2) поднял
вопрос, когда и где возникла задача «Проблема скрещенных лестниц» (CLP)
подвернулся впервые.
«Самая старая известная нам ссылка на CLP датируется 1894 годом.
(Задача 24. The American Mathematical Monthly, 1 (1894), 353-354) »
Раздвижная лестница
Проблемы наверх
…… Лестница стоит только при трении между
верх лестницы и стены и, что более важно, между ногами
лестницы и земли.
5-й
проблема:
Найдите кривую, центр которой
лестницы тянет во время скольжения! …… Предположим, что P (x | y) — точка кривой, а c — длина
лестница.
y = c / 2, если x = 0.- x = c / 2, если y = 0.
Есть теорема Пифагора x² + y² = (c / 2) ².
Это уравнение круга.
Результат: центр
лестница движется по кругу.
Обобщение: какая кривая рисует произвольную
а неподвижная точка лестницы при скольжении?
Astroid …… Если вы начертите все позиции раздвижной лестницы, вы получите
конверт астроида (слева).(2/3)
и c = 2 справа. ……
6-я проблема:
Лестница длиной c = 5м опирается на
стена. Подножие лестницы отрывается от стены со скоростью
v x = 0,3 м / с только тогда, когда расстояние x = 3 м от стены. Как
быстро ли верх лестницы спускается по стене?
Общее решение …… Предположим, что c — длина лестницы.
Предположим, что x (t) и y (t) — расстояния до концов
лестница из угловой стены / земли.
Зависимость от времени дается тегом (t).
v x = x ‘(t) и v y = y’ (t) являются
скорости.
Имеется [x (t)] ² + [y (t)] ² = c².
Вывод равен 2x [x ‘(t)] + 2y [y’ (t)] = 0, следовательно, y ‘(t) = — {x [x’ (t)]} / y (t)}
= — {x [x ‘(t)]} / sqrt {c²- [x (t)] ²} = v y .
Решение с числами
Пусть c = 5m, x = 3m и v x = 0,3 м / с:
v y = -3 * 0,3 / sqrt (5²-3²) м / с = -0,23 м / с
Результат: верхняя часть лестницы движется вниз с
скорость 0,23 м / с.
7-й
Проблема:
Единая лестница длины
l = 5 м, а масса m = 30 кг прислоняется к стене под углом phi = 30 °.
к стене. По трапу поднимается мужчина массой М = 60 кг. Как далеко может
он поднимается до того, как лестница соскользнет? Коэффициент трения между
основание лестницы и грунт f = 1/3. Предположим, что нет трения
вдоль стены.
Решение: Силы
…… Есть вес человека (F P = Mg) и
лестница (F L = мг).
F N и F W — нормальные реакции
у земли и у стены.
Лестницу удерживает сила трения F R
у земли.
Равновесие сил: F W = F R
и F N = F P + F L .
Равновесие моментов около
A: (#) F W * c cos (phi) = F P * s sin (phi) + F L * (c / 2) * sin (phi)
Дальнейший расчет:
Лестница вот-вот соскользнет, когда F R = f
F N есть.Следовательно, вы заменяете F W в (#) на f (F P + F L ):
f (F P + F L ) * c cos (phi) = F P * s
sin (фи) + F L * (с / 2) * грех (фи)
Замените силы массами на F P = Mg и
F L = мг:
f (M + m) * c cos (phi) = M * s sin (phi) + m * (c / 2) * sin (phi) или
(##) cf (M + m) = Ms tan (phi) + m (c / 2) tan (phi)
Изолят:Решение с числами:
Пусть c = 5 м, f = 1/3, m = 30 кг, M = 60 кг и phi = 30 °, тогда
s = 3.1м.
Результат: Мужчина может подняться на 3,1 метра.
The
в последнем расчете решение следующей задачи является частным случаем.
8-я проблема:
Единая лестница длины
c = 5 м, а масса m = 30 кг прислоняется к стене. Предположим, что нет
трение по стене. Коэффициент трения между стопами
лестница и земля f = 1/3.
Под каким углом начинается лестница
скользить?
Решение:
Вставьте M = 0 в (##), и вы получите
fmc = m (c / 2) tan (phi).Следовательно, существует f = (1/2) tan (phi) или phi = arc tan (2f).
Решение
с числами: phi = arc tan (2/3) = 33,7 °.
Результат: Угол между лестницей
а стена всего 33,7 °.
Лестница
Истории наверх
1 Отец несет лестницу.
2 Отец и сын несут лестницу.
3 Ребенок балансирует на лестнице.
4 Цирковой акробат поднимается по лестнице и спускается.
с другой стороны.Может он выполняет стойку на руках сверху или ходит
с лестницей.
Вы можете физически объяснить вопросы, учитывая моменты.
Лестница
Проблемы в Интернете наверх
Немецкий
Бернд Р. Ментес
Das
Leiterproblem (Лейтер-Кисте-Ауфгабе)
Ханс-Юрген Каспар (bei Mathroids Matheplanet))
умереть
Leiter und die Sternkurve (Die Astroid heißt
аух Штернкурве)
Mathematischer Korrespondenzzirkel (Universität Göttingen)
Aufgabe
2 (Лейтер-Кисте-Ауфгабе)
Матроиды Matheplanet Forum Index
Malerarbeit
mit Hindernissen
Aufgabe: Malermeister Patzmann hat ein Problem.Э
soll einen Saal ausmalen und muss dazu erst eine (möglichst lange)
Leiter durch die Kellergänge transportieren. Die Gänge sind rechtwinklig
verzweigt und haben quadratischen Querschnitt, 3m breit und 3m hoch.
Рене Гротманн
Der
Stab, der um die Ecke muss, und einhüllende Kurven
Википедия
Tragbare
Leiter
Английский
Филип Спенсер
Классические заблуждения: A
Лестница будет падать бесконечно быстро, когда ее тянут
Эрик В.Вайсштейн (MathWorld)
скрещено
Задача о лестницах, скрещенные
Теорема о лестницах, перемещение
Задача лестницы
Фрэнк Вольфс
Образец
Проблема 13-3 (Лестница и трение)
Джим Уилсон
Лестница
и проблема с коробкой, Справка
с уравнениями
Марек Сапиль (Лоуренс С. Хуш, визуальный расчет)
Самый короткий
Лестница через забор,
Самая длинная лестница
Торстен Силлке
Лестница-Коробка
Проблема, Лестница-
переместите лестницу за угол, на петлях
Лестница — проблема расстояния
Википедия
скрещено
проблема лестницы
Список литературы
сверху
(1) Мартин Гарднер: Mathematischer Zirkus, Ullstein Berlin
Франкфурт Вена 1988 [USBN 3 550 07692 4]
(2) Кент Холинг (Исследовательский центр Statoil, Тронхейм,
Норвегия): новый взгляд на проблемы лестницы (частный Zugang)
(3) Дункан Грэм и.а .: Уровень математики, Letts Editional
Лондон, 1995 г. [ISBN 1 85758 338 8]
Гейл из побережья Орегона спасибо за поддержку
на моем английском.
Отзыв: Адрес электронной почты на моей главной странице Это
страница также доступна на немецком языке.
URL из
моя домашняя страница:
http://www.mathemische-basteleien.de/
©
2004 Юрген Кёллер
верх
Коэффициент теплопередачи повторно используемого бетонного кирпича в сочетании со стеной из изоляционной плиты EPS
Четыре образца тектонических форм были исследованы для проверки их коэффициентов теплопередачи.Путем анализа и сравнения тестовых значений и теоретических значений коэффициента теплопередачи был предложен метод расчета скорректированного значения для определения коэффициента теплопередачи; Предложенный метод оказался достаточно правильным. Результаты показали, что коэффициент теплопередачи кирпичной стены из переработанного бетона выше, чем у стены из глиняного кирпича, коэффициент теплопередачи кирпичной стены из переработанного бетона может быть эффективно снижен в сочетании с изоляционной панелью из пенополистирола, а тип теплоизоляции сэндвич был лучше. чем у типа внешней теплоизоляции.
1. Введение
По мере того, как урбанизация постепенно расширяется, также увеличиваются высокие темпы строительства зданий и выдающиеся достижения в области энергосбережения [1]. Энергосбережение играет важную роль в национальных энергетических стратегиях, снижая значительную нагрузку на ресурсы и окружающую среду [2, 3]. В элементах частокола здания площадь внешней стены занимает большую долю по сравнению с крышей здания, дверями, окнами и т. Д. [4, 5].Тепловая консервация наружных стен является ключом к достижению энергоэффективности в зданиях [5, 6]. Наружные стены различаются в зависимости от строительных материалов, типов конструкций и условий окружающей среды. Глиняный кирпич, широко используемый во многих существующих зданиях, привел к огромным разрушениям земельных ресурсов. Производственный процесс с использованием высокотемпературных печей также привел к увеличению выбросов парниковых газов. Таким образом, возникла растущая потребность в исследованиях строительных материалов для зеленых стен и их термоконсервации и теплоизоляционных характеристик.Переработанный бетонный кирпич, изготовленный из измельченных отходов бетона, широко используется в кирпичных конструкциях в качестве экологически чистых строительных материалов. Было проведено множество исследований его механических свойств, но лишь несколько измерений его теплоизоляционных свойств [7]. Кроме того, наиболее распространенным типом теплоизоляции было добавление теплосохраняющих материалов на внешней стороне наружной стены, с самым большим ограничением в виде более короткого срока службы [8, 9]. Вспениваемый полистирол (EPS), используемый для теплоизоляции, продемонстрировал очевидные свойства сохранения тепла и теплоизоляции.Тем не менее, различные материалы для наружных стен с различными формами структурных типов для сохранения тепла из пенополистирола, независимо от того, сильно ли отличаются вариации их теплоизоляционных свойств, традиционно не были в центре внимания в контексте сохранения тепла стен и энергосбережения.
Коэффициент теплопередачи () обычно использовался в качестве показателя для измерения термоконсервации и теплоизоляции стен корпуса и в основном определялся коэффициентом теплопроводности () материалов.Считается, что тепловая и влажная среда влияет на характеристики теплообмена стенок корпуса [10–12]. Коэффициент теплопроводности изменяется в зависимости от температуры и влажности воздуха, что приводит к отклонению между фактическим и теоретическим значением. Однако во многих исследованиях предполагалось, что характеристики материала не изменятся или коэффициент теплопроводности () материалов выражен как постоянный. Поэтому существует растущая потребность в изучении скорректированного коэффициента теплопроводности материала в различных средах и его расширенном применении в энергосберегающих конструкциях.
Переработанный бетонный кирпич имеет все больший потенциал для развития и использования. Его различное сочетание с изоляционной плитой EPS имеет как эффект экологической защиты окружающей среды, так и энергосбережение. Понимание характеристик теплопередачи вторичного бетонного кирпича в сочетании с изоляционной плитой из пенополистирола становится все более необходимым для количественной оценки их вклада в энергосбережение.
Целями этого исследования было испытание коэффициента теплопередачи () кирпичной стены из вторичного бетона, прямое сравнение теплового поведения различных строительных решений стен и предложение скорректированного метода расчета коэффициента теплопередачи при оптимизации энергопотребления здания. .
2. Испытание коэффициента теплопередачи
В настоящее время не существует официального стандарта для методов испытаний, которые непосредственно касаются динамических характеристик стен: основные эталонные нормы [13] включают измерение стационарных характеристик одинарных материалов и многослойных конструкций. при стандартных граничных условиях. В этом исследовании был проведен экспериментальный анализ с климатической камерой для сравнения влияния коэффициента теплопередачи элементов оболочки, которые характеризуются эквивалентными характеристиками в установившемся режиме.
2.1. Типы стен и свойства материалов
В этом исследовании были изготовлены четыре различных образца для количественной оценки их тепловых характеристик. Четыре образца, которые были отобраны среди типологий стен, подробно описаны на рисунке 1 и в таблице 1.
Типы образцов Слои Толщина
(м) Проводимость
( Вт м −1 K −1 ) Плотность
(кг · м −3 )
SJ0 Стена из глиняного кирпича 0.240 0,508 1662
SJ1 Кирпич из вторичного бетона стеновой 0,240 0,708 1887 0,708 1887 9207 9207 907 9207 9207 9207 9207 0,930 [16] 1990 2 изоляционные плиты EPS 0,060 0,042 [16] 29,50 3 стены из вторичного бетона 0.240 0,708 1887
SJ3 1 кирпичная стена из переработанного бетона 0,115 0,708 1887 51 907 раствор
1990 3 Изоляционная плита EPS 0,060 0,042 [16] 29,50 4 цементный раствор 0,010 0.930 [16] 1990 Стена из 5 кирпичей из переработанного бетона 0,115 0,708 1887
кирпичная стена SJ0; SJ1 была переработана бетонная кирпичная стена; SJ2 добавлен односторонний шаблон EPS на базе SJ1; SJ3 был добавлен в шаблон EPS в середине SJ1.
2.2. Устройство для испытаний
В соответствии со стандартами и исследованиями, относящимися к этому типу испытаний [14, 15], в экспериментальном исследовании использовалось устройство для измерения стационарной теплопередачи (CD-WTFl515, Шэньян, Китай).Условие теплопередачи тестируемой оболочки здания моделируется на основе стандарта GB / T 13475-2008 и однонаправленного устойчивого принципа теплопередачи для измерения и анализа коэффициента теплопередачи. Климатическая установка с контролем окружающей среды состоит из двух камер с кондиционированием воздуха, в которых температура регулируется с помощью термостойких проводов и систем охлаждения (рисунки 2 и 3). Одна камера используется для создания микроклимата на открытом воздухе. Температура дозирующего резервуара установлена на -10 ° C (при допустимом перепаде температур ± 0.2 ° С). Другая камера имитирует внутреннюю среду, в которой температура установлена на 35 ° C (с допустимым перепадом температур ± 0,1 ° C). Образцы были изготовлены в соответствии с предусмотренными размерами испытательного оборудования. Размеры установки и образцов составляют 2600 × 2160 × 2140 мм в высоту и 1500 × (≤400) × 1500 мм соответственно (рисунок 4). После 28 дней естественной сушки в испытательном устройстве поверхность раздела между образцами и испытательным устройством была герметизирована пенополиуретаном.
Все образцы были испытаны в Пекинском центре испытаний строительных материалов. Перед обработкой образцов стен в аппарате сначала была проведена калибровка установки. Образцы стен внутри и снаружи должны соответствовать горячей и холодной камерам соответственно. Для каждого образца шесть групп данных связанных параметров окружающей среды, таких как температура горячего поля () и холодного поля (), влажность горячего поля () и холодного поля (
Основное руководство по расчету падений и градиентов для дренажа | Основное руководство по расчету падений и уклонов для дренажа
Градиенты трубы
Все наземные и подземные горизонтальные дренажные трубы должны быть проложены с соответствующим уклоном.
Градиенты от 1 на 40 до 1 на 110 обычно дают адекватные скорости потока.
Уклон 1 к 80 подходит для начала расчетов схем трубопроводов.
Если уклон недостаточно крутой, т. Е. меньше 1: 110, , тогда труба может заблокироваться, если твердые частицы замедлятся и станут скрученными. Падение в трубе может быть определено как вертикальная величина, на которую труба опускается дистанция. Расстояние может быть между участками трубы или между люками.На схеме ниже показано падение трубы и расстояние.
Уклон можно определить как падение, разделенное на расстояние.
ГРАДИЕНТ = ПАДЕНИЕ / РАССТОЯНИЕ
Например, 24-метровый участок дренажной трубы имеет падение 0,30 метра, рассчитайте уклон.
Градиент = 0,30 / 24
Градиент = 0,0125
Его можно преобразовать в градиент, записанный как отношение или 1: некоторое число.
Градиент = 1 / 0,0125 = 80
Градиент = 1 из 80
Вышеупомянутая формула может быть изменена для Fall, если градиент известен:
ПАДЕНИЕ = ГРАДИЕНТ X РАССТОЯНИЕ
Например, рассчитайте падение на 50-метровом участке трубопровода для загрязненной воды, если уклон должен быть 1 к 80.
Градиент 1 к 80 преобразуется в число, а не в коэффициент.
1/80 = 0,0125
Падение = Градиент x Расстояние
Падение = 0,0125 x 50
Падение = 0,625 метра или 625 мм.
Предыдущую диаграмму можно дополнить добавлением уклона трубы.
Инвертировать уровни
Уровень Инвертировать трубы — это уровень, снимаемый с нижней части внутренней части трубы, как показано ниже.
Уровень гребня трубы равен Инвертировать уровень плюс внутренний диаметр трубы плюс толщина стенки трубы. Может потребоваться использовать это в расчетах, когда измерения уровня производятся на вершине трубы.
Люки
Люк или камера доступа требуется для доступа к дренажной системе для разблокировки, очистки, установки стержней или осмотра. Типичный люк показан ниже.
Люки могут изготавливаться из кирпича или сборного железобетона. Иногда несколько колец из сборного железобетона используются для образования люка, что ускоряет процесс строительства на месте. Обычно в колодцы глубиной менее 1,0 м глубиной требуются ступеньки для облегчения доступа рабочего.
Люки и смотровые люки также изготавливаются из ПВХ. Камера доступа обычно не достаточно велика, чтобы принять человека, но подходит для доступа с помощью чистящих стержней или шланга, и они используются для домашнего применения, обычный размер пластиковой камеры доступа составляет 450 мм в диаметре.Для внутреннего рынка могут использоваться крышки из пластика, стекловолокна или оцинкованной стали, но крышки из чугуна требуются в местах пересечения дорожного движения.
Люк с обратным отводом используется в областях, где уровень поверхности наклонен, как показано ниже.
Если подземная канализационная труба должна оставаться под землей, она должна соответствовать среднему уклону уклона. Это всегда означает, что уклон трубы становится слишком крутым , в результате чего твердые частицы и остаются скрученными в трубе, вызывая закупорку.
Чтобы решить эту проблему, был разработан люк с обратным отводом, как показано ниже.
Более простой способ построить люк с обратным отводом — использовать внутренний вертикальный участок трубы, как показано ниже.
Для получения дополнительной информации и рекомендаций см. Следующий документ.
Железобетонные консольные подпорные стены:
Подпорных стен Дизайн Формула Куломба-Ренкина
- Рассчитать коэффициент активного давления грунта,
давление грунта, горизонтальная результирующая и момент.
Доплата за равномерную нагрузку на грунт
- Расчет давления грунта по горизонтали
в результате единой надбавки за загрузку.
Доплата за точечную нагрузку на грунт
- Расчет давления грунта по горизонтали
в результате надбавки за точечную нагрузку.
Доплата за загрузку полосы почвы
- Расчет давления грунта по горизонтали
в результате надбавки за загрузку полосы.
Доплата за грунтовую нагрузку на рампу
- Расчет давления грунта по горизонтали
в результате надбавки за нагрузку на рампу.
Доплата за треугольную нагрузку на грунт
- Расчет давления грунта по горизонтали
в результате надбавки за треугольную нагрузку.
Линия
загрузка грунта надбавка
- Расчет давления грунта по горизонтали
в результате надбавки за линейную нагрузку.
Угол скольжения
- Рассчитайте угол скольжения почвы для давления почвы
расчет клина, непосредственно для несвязных грунтов и методом проб и ошибок для
связные грунты.
Метод клина
- Рассчитайте результирующее давление почвы с помощью или
без поверхностной наценки приблизительным клиновым методом.
Раздел
дизайн Trial подпорной стены
- Создание бетонной консольной подпорной стенки
раздел пробного дизайна.
Устойчивость к
раздвижной — без ключа
- Рассчитать сопротивление скольжения для подпорной стенки без
база с ключами.
Устойчивость к скольжению —
ключ
- Рассчитать сопротивление скольжения для подпорной стенки с
база под ключ.
Эксцентриситет, макс. И мин.
давление почвы
- Рассчитайте эксцентриситет, максимальное и минимальное давление на грунт
под основанием подпорной стенки.
Результирующее давление в подшипниках
- Вычислить результанты Подшипник давления для пальцев и пятки
бетонной консольной подпорной стенки для использования в арматуре
расчеты.
Проверить несущую способность
- Проверить несущую способность бетонного консольного крепления
стена.
Арматура стержневой секции
- Рассчитайте расстояние до стали и площадь стали
арматура для стволовой части бетонной консольной подпорной стенки.
Усиление пяточной части
- Рассчитайте расстояние до стали и площадь стали
армирование пяточной части основания бетонной консоли
подпорная стена.
Усиление носка
- Рассчитайте расстояние до стали и площадь стали
усиление носка основания бетонной консольной опоры
стена.
Разработка стержневой стали
длина
- Рассчитайте развернутую длину стальной арматуры
шток сечение бетонной консольной подпорной стенки.
Задача дизайна 1
- Рассчитайте боковую силу грунта, действующую на подпорную стену, с помощью метода клина.
Задача дизайна 2
- Рассчитайте боковую силу грунта, действующую на подпорную стену, с помощью формулы Ренкина.
Задача проектирования 3
- Проверьте сопротивление скольжения для подпорной стенки.
Задача дизайна 4
- Проверьте сопротивление скольжению, устойчивость оборота, несущую способность и рассчитать требуемые участки стальной арматуры для предлагаемой подпорной стенки.
Вес) Также прочтите: Введение в портальную балку | Нагрузка на портальный желоб | Тип нагрузки на козловой желоб
Также прочтите: Разница между битумом и гудроном | Что такое битум | Что такое смола
Номинальная толщина
Глубина арматуры (дюймы)
Центр
Край
6 «
2.75 «
2,75 дюйма
8 «
3,75 дюйма
5,25 дюйма
10 «
4,75 дюйма
7,25 дюйма
12 «
5,75 дюйма
9,0 «
14 «
6.75 «
11,0 «
16 «
7,75 дюйма
13,0 «
Задачи лестничной диаграммы
Что такое лестничная задача?
| Задача лестницы — это задача, связанная с лестницей. |
Две задачи являются классическими, проблема лестничной коробки (рисунок)
и проблема скрещенных лестниц.
Они особенные, потому что проблема простая, но
расчет усложняется.
Проблема со стеной лестницы
сверху
Следующую задачу можно найти в школьной книге в
связь с теоремой Пифагора.
| …… | 1-я проблема: Лестница длиной c = 7м прислоненная к стена с основанием d = 1.4 м от стены у основания. На какой высоте лестница касается стены? |
Решение: c² = h² + d², следовательно, h = sqrt (c²-d²) = sqrt (7²-1,4²) m = 6,9 м.
Результат: лестница касается стены на высоте 6,9 м.
Когда функция косинуса
вводится, вы можете найти угол наклона.
Имеется cos (alpha) = d / c. Тогда вы получите alpha = arc cos (d / c) = arc
cos (1,4 / 7) = 78,5 °.
Проблема с лестничной коробкой
сверху
Если вы говорите о проблеме лестницы, вы обычно имеете в виду
следующая проблема.
| …… | 2-я проблема: Ящик в форме куба с краем длиной 1м стоит перед стеной. Лестница длиной 5 м опирается на стены и просто касается коробки краем. Как высоко на стене наверху лестницы? |
Два решения
| …… | Очевидно, есть два способа опереться на лестницу у стены. Вы часто спрашиваете максимальную высоту, поэтому проблема |
Формула
| …… | Неразумно указывать высоту у стены и расстояние от ступни лестницы от стены в качестве переменных. Расчет проще с x и y из-за |
Есть два уравнения:
Теорема Пифагора гласит (#) c² = (b + x) ² + (b + y) ².
Есть два похожих треугольника (желтые), и у вас
(##) x : b = b : y.
Если вы изолировали y в (##) и поместили y в (#), вы получите c² = (b + x) ² + (b + b² / x) ²
или x 4 + 2bx³ + (2b²-c²) x² + 2b³x + b 4 = 0.
Это уравнение 4-й степени.
Приблизительно
решение
Имеется b = 1 и c = 5. Это приводит к уравнению x 4 + 2x³-23x² + 2x + 1 = 0.
Вы найдете приблизительное решение, исследуя
график функции f (x) = (x 4 + 2x³-23x² + 2x + 1) / 64
и найдя точки на оси абсцисс.Коэффициент 1/64 произвольный и
делает возможным красивый график.
Высота лестницы 3,84 м + 1 м = 4,84 м при x = 0,26.
и y = 1 / x = 3,84.
Или высота лестницы 1,26 м при x = 3,84 и
у = 1 / х = 0,26.
точно
решение
Вы можете использовать p-q-формулу квадратного уравнения
решить x 4 + 2x³-23x² + 2x + 1 = 0.
Сначала вы кладете c = 5 и b = 1, а затем y = 1 / x. В уравнение
(#) c² = (x + b) ² + (y + b) ².
Вы получаете (x + 1) ² + (y + 1) ² = 25 или (x + 1) ² + (1 / x + 1) ² = 25
или x² + 2x + 1 + 1 / x² + 2 / x + 1 = 25 или [x² + 2 + 1 / x²] + [2x + 2 / x] = 25.
Имеются z² = x² + 2 + 1 / x² и 2z = 2x + 2 / x. с
г = х + 1 / х.
Таким образом, вы получаете квадратное уравнение относительно z: z² + 2z = 25 = 0.
Дальнейший расчет:
Результат: лестница достигает высоты 4,84 м или 1,26 м.
Решение с помощью
тригонометрические формулы, присланные Каваном Оруэллом
| …… | Проблема описана снова Имеется лестница длиной c, прислоненная к вертикали. стена.Он просто касается угла квадратной коробки размером b x b. Какова высота лестницы до стены? Обратите внимание на угол t в этом решении. |
Пусть b = 1 и c = 5.
Вы получаете 5 = 1 / sin (t) + 1 / cos (t), потому что
похожих треугольников
и 5 = [sin (t) + cos (t)] / [sin (t) cos (t)]
порядок 5 [sin (t) cos (t)] = sin (t) + cos (t).
Есть тригометрическая идентичность
sin (2t) = 2 sin (t) cos (t).
Тогда существует 2,5sin (2t) = sin (t) + cos (t).
Возведение в квадрат дает 6,25sin² (2t) = [sin (t) + cos (t)] ² = sin² (t) + 2sin (t) cos (t) + cos² (t) = 2sin (t) cos (t) +1
потому что sin² (t) + cos² (t) = 1.
Это дает 6,25sin² (2t) = sin (2t) +1.
Это квадратное уравнение в
sin (2t) = y, 6,25y² = y + 1 или y²-0,16y-0,16 = 0.
Есть решения y 1 = 0,08 + sqrt (0,1664)
и y 2 = 0,08-sqrt (0,1664).
y = sin (2t) дает
sin (2t 1 ) = 0,08 + sqrt (0,1664) или 2t 1 = 29,20 °
или 2t 2 = 180 ° -29,2 ° = 150,80 °.
Формула h = c * sin (t) дает h 1 = 5 * sin (t 1 ) = 5 * sin (14.60 °) = 1,26
или ч 2 = 5 * sin (t 2 ) = 5 * sin (75,40 °) = 4,84 .
Решение y 2 = 0,08-sqrt (0,1664) есть
отрицательный и ведет к углам, которые невозможны для лестницы.
Варианты
> Вы можете искать целые числа как решения
уравнения 4-й степени.
> Вы можете заменить куб на
твердый.
> Вы можете рассчитать соотношение как
лестница разделена на две части.
| …… | > Можно куб сжать. Тогда вы можете интерпретировать лестницу задача как расчет треугольника. Задайте сторону c, угол гаммы и биссектриса w гамма в произвольном треугольнике. Найдите сторону a. Имеется гамма = 90 ° для проблема лестницы. |
Подробнее об этой задаче лестницы
на домашней странице Торстена Силлке (URL-адрес ниже).
Здесь вы также обнаружите, что Ньютон даже работал
по проблеме «отрезок в углу».
Кент Холинг (2) поднял вопрос, когда и где
задача «Задача с одной лестницей» возникла впервые.
«Самая старая известная нам ссылка на проблему квадратного ящика.
датируется 1754 годом. (Томас Симпсон: Трактат по алгебре, Джон Норс, Ломндон
1745, стр. 250). Самая старая известная нам справочная информация по общей проблеме коробки
с 1907 г. (А.Сирил Пирсон: Стандартная книга-головоломка двадцатого века,
George Routledge & Sons, Ltd., Лондон, 1907 г., стр. 103.) »
Проблема угла лестницы
сверху
| …… | 3-я проблема: Имеется лестница длиной c и коридор шириной b. К сожалению, коридор имеет право угловой изгиб. Какой длины может быть лестница, чтобы ее можно было перемещать по угол? |
Это максимальная проблема.Длина лестницы c (или
c² для расчетов) должно иметь максимальное значение.
| …… | Теорема Пифагора приводит к (#) c² = (x + b) ² + (y + b) ². Имеется (##) ist y : b = b : x или y = b² / x из-за похожих желтых треугольников. . Если вы замените y на (#), вы получите функцию c² = (x + b) ² + (b² / x + b) ² или c² = x² + 2bx + b 4 / x² + 2b³ / x + 2b². Первая производная: (c²) ‘= 2x + 2b-2b 4 / x³-2b³ / x².(Вторая производная положительна при x> 0) |
(c²) ‘= 0 приводит к уравнению 4-й степени x 4 + bx³-b³x-b 4 = 0.
Вы легко узнаете, что x = b — решение.
x = b приводит к c / 2 = sqrt (b) или c = 2sqrt (2) b. Это решение
показано на рисунке выше.
Результат: Лестница длиной c = 2sqrt (2) b является
самый длинный.
Более общее решение —
прислал Йохан Асма
| Удобно ввести переменную be p, так что b + pb = (1 + p) b — отрезок горизонтальной линии. Тогда существует x: (a + x) = b: [(1 + p) b] или x = a / p. Теорема Пифагора дает c² = (a + a / p) ² + (b + pb) ² Вы ищите значение p так, чтобы c = c (p) было минимумом. |
Вам нужна первая производная c ‘или попроще (c²)’ = a² (-2 / p²-2 / p³) + b² (2 + 2p).
(c²) ‘= 0 дает a² (-2 / p²-2 / p³) + b² (2 + 2p) = 0
или a² (-2p-2) + b² (2p³ + 2p 4 ) или -2a² (p + 1) + 2b²p³ (1 + p)
или (-2a² + 2p³b²) (p + 1) = 0.
Решение: p³ = a² / b² или p = (a / b) 2/3 .
Пусть b = a. Тогда p = 1 и c² = a² (1 + 2 / p + 1 / p²) + b² (1 + 2p + p²) = b² (1 + 2 + 1) + b² (1 + 2 + 1) = 8b².
или c = 2sqrt (2) b.
Так же проблему можно дать
как проблема с лестницей:
Ящик в форме куба с краем
длиной 1м стоит перед стеной. Лестница прислоняется к стене и
просто касается коробки краем. Какова самая короткая лестница?
Ханс-Иоахим
Саймон прислал мне следующее решение.
Переходные лестницы
Проблема наверх
Мартин Гарднер (1) опубликовал следующую задачу и
он стал популярным. Начать решение легко, но тогда оно будет выглядеть как
сложно, как проблема с лестницей.
| …… | 4-я проблема: Между двумя лестницами две дома. Как долго расстояние x между стены дома, если длина лестниц a и b и высота c над землей перехода даны? |
Попытка
решения
| Вы вводите четыре переменные h, k, y и z (рисунок) Имеется (#) y: c = x: h и z: c = x: k из-за похожих треугольников. |
Изолируйте h и k в (##) и сначала замените их в (#)
а затем в (###). Вы получаете:
Если вы хотите удалить корни, вы должны возвести уравнения в квадрат
дважды.
Тогда вы получите уравнение 8-й степени :-(.
Решение
как замена
Вы не рассчитываете расстояние до стены напрямую
но через высоту h более длинной лестницы.
Вы получаете 1 = c / h + c / k и k = ch / (h-c) с (#) и (##).
(##) дает a²-h² = b²-k².
Если вы замените k = ch / (h-c) на a²-h² = b²-k²,
вы получите h 4 -2ch 3 — (a²-b²) h² + 2c (a²-b²) h-c² (a²-b²) = 0
после нескольких шагов.
Пример с числами
| …… | Вы рисуете лестницы a = 8,0 и b = 7,0 между двумя стены шириной x = 5. Тогда c = 2,8. Блок может быть высотой 1 м для лестниц. Тогда уравнение 4-й степени имеет вид h 4 -5,6h 3 -15h² + 84h-117,6 = 0. | …… |
Результат: Чертеж и расчет дают примерно одинаковые результаты.
Привлечение проблемы в рекреационной
математика не в том, чтобы определить расстояние до стен дома.Это вызов
найти целых чисел в качестве значений и как можно меньших целых чисел
для разной длины.
Вы найдете коллекцию в книге Гарднера.
Кент Холинг (2) поднял
вопрос, когда и где возникла задача «Проблема скрещенных лестниц» (CLP)
подвернулся впервые.
«Самая старая известная нам ссылка на CLP датируется 1894 годом.
(Задача 24. The American Mathematical Monthly, 1 (1894), 353-354) »
Раздвижная лестница
Проблемы наверх
| …… | Лестница стоит только при трении между верх лестницы и стены и, что более важно, между ногами лестницы и земли. |
5-й
проблема:
Найдите кривую, центр которой
лестницы тянет во время скольжения!
| …… | Предположим, что P (x | y) — точка кривой, а c — длина лестница. y = c / 2, если x = 0.- x = c / 2, если y = 0. Есть теорема Пифагора x² + y² = (c / 2) ². Это уравнение круга. |
Результат: центр
лестница движется по кругу.
Обобщение: какая кривая рисует произвольную
а неподвижная точка лестницы при скольжении?
Astroid
| …… | Если вы начертите все позиции раздвижной лестницы, вы получите конверт астроида (слева).(2/3) и c = 2 справа. | …… |
6-я проблема:
Лестница длиной c = 5м опирается на
стена. Подножие лестницы отрывается от стены со скоростью
v x = 0,3 м / с только тогда, когда расстояние x = 3 м от стены. Как
быстро ли верх лестницы спускается по стене?
Общее решение
| …… | Предположим, что c — длина лестницы. Предположим, что x (t) и y (t) — расстояния до концов лестница из угловой стены / земли. Зависимость от времени дается тегом (t). v x = x ‘(t) и v y = y’ (t) являются скорости. |
Имеется [x (t)] ² + [y (t)] ² = c².
Вывод равен 2x [x ‘(t)] + 2y [y’ (t)] = 0, следовательно, y ‘(t) = — {x [x’ (t)]} / y (t)}
= — {x [x ‘(t)]} / sqrt {c²- [x (t)] ²} = v y .
Решение с числами
Пусть c = 5m, x = 3m и v x = 0,3 м / с:
v y = -3 * 0,3 / sqrt (5²-3²) м / с = -0,23 м / с
Результат: верхняя часть лестницы движется вниз с
скорость 0,23 м / с.
7-й
Проблема:
Единая лестница длины
l = 5 м, а масса m = 30 кг прислоняется к стене под углом phi = 30 °.
к стене. По трапу поднимается мужчина массой М = 60 кг. Как далеко может
он поднимается до того, как лестница соскользнет? Коэффициент трения между
основание лестницы и грунт f = 1/3. Предположим, что нет трения
вдоль стены.
Решение:
Силы
| …… | Есть вес человека (F P = Mg) и лестница (F L = мг). F N и F W — нормальные реакции у земли и у стены. Лестницу удерживает сила трения F R у земли. |
Равновесие сил: F W = F R
и F N = F P + F L .
Равновесие моментов около
A: (#) F W * c cos (phi) = F P * s sin (phi) + F L * (c / 2) * sin (phi)
Дальнейший расчет:
Лестница вот-вот соскользнет, когда F R = f
F N есть.Следовательно, вы заменяете F W в (#) на f (F P + F L ):
f (F P + F L ) * c cos (phi) = F P * s
sin (фи) + F L * (с / 2) * грех (фи)
Замените силы массами на F P = Mg и
F L = мг:
f (M + m) * c cos (phi) = M * s sin (phi) + m * (c / 2) * sin (phi) или
(##) cf (M + m) = Ms tan (phi) + m (c / 2) tan (phi)
Изолят:
Решение с числами:
Пусть c = 5 м, f = 1/3, m = 30 кг, M = 60 кг и phi = 30 °, тогда
s = 3.1м.
Результат: Мужчина может подняться на 3,1 метра.
The
в последнем расчете решение следующей задачи является частным случаем.
8-я проблема:
Единая лестница длины
c = 5 м, а масса m = 30 кг прислоняется к стене. Предположим, что нет
трение по стене. Коэффициент трения между стопами
лестница и земля f = 1/3.
Под каким углом начинается лестница
скользить?
Решение:
Вставьте M = 0 в (##), и вы получите
fmc = m (c / 2) tan (phi).Следовательно, существует f = (1/2) tan (phi) или phi = arc tan (2f).
Решение
с числами: phi = arc tan (2/3) = 33,7 °.
Результат: Угол между лестницей
а стена всего 33,7 °.
Лестница
Истории наверх
1 Отец несет лестницу.
2 Отец и сын несут лестницу.
3 Ребенок балансирует на лестнице.
4 Цирковой акробат поднимается по лестнице и спускается.
с другой стороны.Может он выполняет стойку на руках сверху или ходит
с лестницей.
Вы можете физически объяснить вопросы, учитывая моменты.
Лестница
Проблемы в Интернете наверх
Немецкий
Бернд Р. Ментес
Das
Leiterproblem (Лейтер-Кисте-Ауфгабе)
Ханс-Юрген Каспар (bei Mathroids Matheplanet))
умереть
Leiter und die Sternkurve (Die Astroid heißt
аух Штернкурве)
Mathematischer Korrespondenzzirkel (Universität Göttingen)
Aufgabe
2 (Лейтер-Кисте-Ауфгабе)
Матроиды Matheplanet Forum Index
Malerarbeit
mit Hindernissen
Aufgabe: Malermeister Patzmann hat ein Problem.Э
soll einen Saal ausmalen und muss dazu erst eine (möglichst lange)
Leiter durch die Kellergänge transportieren. Die Gänge sind rechtwinklig
verzweigt und haben quadratischen Querschnitt, 3m breit und 3m hoch.
Рене Гротманн
Der
Stab, der um die Ecke muss, und einhüllende Kurven
Википедия
Tragbare
Leiter
Английский
Филип Спенсер
Классические заблуждения: A
Лестница будет падать бесконечно быстро, когда ее тянут
Эрик В.Вайсштейн (MathWorld)
скрещено
Задача о лестницах, скрещенные
Теорема о лестницах, перемещение
Задача лестницы
Фрэнк Вольфс
Образец
Проблема 13-3 (Лестница и трение)
Джим Уилсон
Лестница
и проблема с коробкой, Справка
с уравнениями
Марек Сапиль (Лоуренс С. Хуш, визуальный расчет)
Самый короткий
Лестница через забор,
Самая длинная лестница
Торстен Силлке
Лестница-Коробка
Проблема, Лестница-
переместите лестницу за угол, на петлях
Лестница — проблема расстояния
Википедия
скрещено
проблема лестницы
Список литературы
сверху
(1) Мартин Гарднер: Mathematischer Zirkus, Ullstein Berlin
Франкфурт Вена 1988 [USBN 3 550 07692 4]
(2) Кент Холинг (Исследовательский центр Statoil, Тронхейм,
Норвегия): новый взгляд на проблемы лестницы (частный Zugang)
(3) Дункан Грэм и.а .: Уровень математики, Letts Editional
Лондон, 1995 г. [ISBN 1 85758 338 8]
Гейл из побережья Орегона спасибо за поддержку
на моем английском.
Отзыв: Адрес электронной почты на моей главной странице
Это
страница также доступна на немецком языке.
URL из
моя домашняя страница:
http://www.mathemische-basteleien.de/
©
2004 Юрген Кёллер
верх
| Типы образцов | Слои | Толщина (м) | Проводимость ( Вт м −1 K −1 ) | Плотность (кг · м −3 ) | |||||
| SJ0 | Стена из глиняного кирпича | 0.240 | 0,508 | 1662 | |||||
| SJ1 | Кирпич из вторичного бетона стеновой | 0,240 | 0,708 | 1887 | 0,708 | 1887 | 9207 9207 907 9207 9207 9207 9207 | 0,930 [16] | 1990 |
| 2 изоляционные плиты EPS | 0,060 | 0,042 [16] | 29,50 | ||||||
| 3 стены из вторичного бетона | 0.240 | 0,708 | 1887 | ||||||
| SJ3 | 1 кирпичная стена из переработанного бетона | 0,115 | 0,708 | 1887 | 1990 | ||||
| 3 Изоляционная плита EPS | 0,060 | 0,042 [16] | 29,50 | ||||||
| 4 цементный раствор | 0,010 | 0.930 [16] | 1990 | ||||||
| Стена из 5 кирпичей из переработанного бетона | 0,115 | 0,708 | 1887 | ||||||
Железобетонные консольные подпорные стены:
Формула Куломба-Ренкина
- Рассчитать коэффициент активного давления грунта,
давление грунта, горизонтальная результирующая и момент.
Доплата за равномерную нагрузку на грунт
- Расчет давления грунта по горизонтали
в результате единой надбавки за загрузку.
Доплата за точечную нагрузку на грунт
- Расчет давления грунта по горизонтали
в результате надбавки за точечную нагрузку.
Доплата за загрузку полосы почвы
- Расчет давления грунта по горизонтали
в результате надбавки за загрузку полосы.
Доплата за грунтовую нагрузку на рампу
- Расчет давления грунта по горизонтали
в результате надбавки за нагрузку на рампу.
Доплата за треугольную нагрузку на грунт
- Расчет давления грунта по горизонтали
в результате надбавки за треугольную нагрузку.
Линия
загрузка грунта надбавка
- Расчет давления грунта по горизонтали
в результате надбавки за линейную нагрузку.
Угол скольжения
- Рассчитайте угол скольжения почвы для давления почвы
расчет клина, непосредственно для несвязных грунтов и методом проб и ошибок для
связные грунты.
Метод клина
- Рассчитайте результирующее давление почвы с помощью или
без поверхностной наценки приблизительным клиновым методом.
Раздел
дизайн Trial подпорной стены
- Создание бетонной консольной подпорной стенки
раздел пробного дизайна.
Устойчивость к
раздвижной — без ключа
- Рассчитать сопротивление скольжения для подпорной стенки без
база с ключами.
Устойчивость к скольжению —
ключ
- Рассчитать сопротивление скольжения для подпорной стенки с
база под ключ.
Эксцентриситет, макс. И мин.
давление почвы
- Рассчитайте эксцентриситет, максимальное и минимальное давление на грунт
под основанием подпорной стенки.
Результирующее давление в подшипниках
- Вычислить результанты Подшипник давления для пальцев и пятки
бетонной консольной подпорной стенки для использования в арматуре
расчеты.
Проверить несущую способность
- Проверить несущую способность бетонного консольного крепления
стена.
Арматура стержневой секции
- Рассчитайте расстояние до стали и площадь стали
арматура для стволовой части бетонной консольной подпорной стенки.
Усиление пяточной части
- Рассчитайте расстояние до стали и площадь стали
армирование пяточной части основания бетонной консоли
подпорная стена.
Усиление носка
- Рассчитайте расстояние до стали и площадь стали
усиление носка основания бетонной консольной опоры
стена.
Разработка стержневой стали
длина
- Рассчитайте развернутую длину стальной арматуры
шток сечение бетонной консольной подпорной стенки.
Задача дизайна 1
- Рассчитайте боковую силу грунта, действующую на подпорную стену, с помощью метода клина.
Задача дизайна 2
- Рассчитайте боковую силу грунта, действующую на подпорную стену, с помощью формулы Ренкина.
Задача проектирования 3
- Проверьте сопротивление скольжения для подпорной стенки.
Задача дизайна 4
- Проверьте сопротивление скольжению, устойчивость оборота, несущую способность и рассчитать требуемые участки стальной арматуры для предлагаемой подпорной стенки.